Application of Derivatives 4 Question 30
####32. The function $f(x)=2|x|+|x+2|-|| x+2|-2| x||$ has a local minimum or a local maximum at $x$ is equal to
(2013 Adv.)
(a) -2
(b) $\frac{-2}{3}$
(c) 2
(d) $2 / 3$
Show Answer
Answer:
Correct Answer: 32. $(a, b)$
Solution:
- PLAN
$ \begin{aligned} & \text { We know that, }|x|=\begin{array}{c} x, \quad \text { if } x \geq 0 \\ -x, \quad \text { if } x<0 \end{array} \\ & \Rightarrow \quad|x-a|=\begin{array}{cc} x-a, & \text { if } x \geq a \\ -(x-a), & \text { if } x<a \end{array} \end{aligned} $
and for non-differentiable continuous function, the maximum or minimum can be checked with graph as
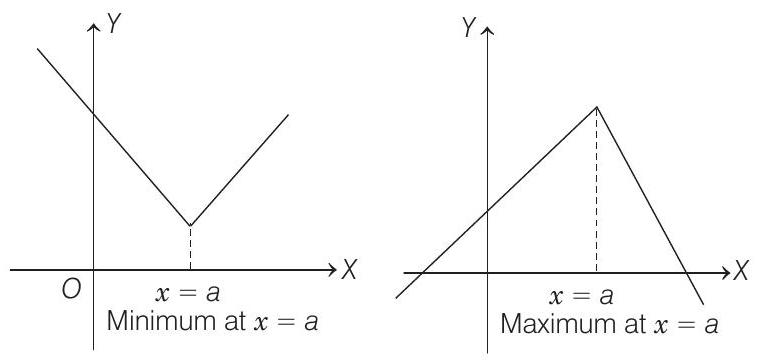
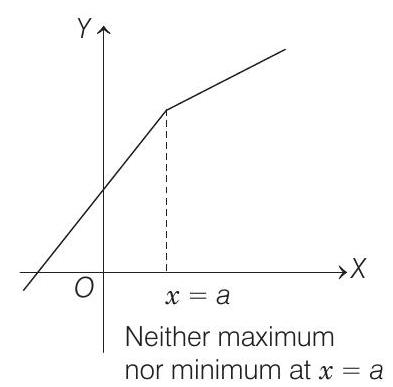
Here, $f(x)=2|x|+|x+2|-|| x+2|-2| x||$ $-2 x-(x+2)+(x-2)$, if when $x \leq-2$ $-2 x+x+2+3 x+2, \quad$ if $\quad$ when $-2<x \leq-2 / 3$
$ \begin{aligned} & =\quad-4 x, \quad \text { if } \text { when }-\frac{2}{3}<x \leq 0 \\ & 4 x, \quad \text { if when } 0<x \leq 2 \\ & 2 x+4, \quad \text { if } \quad \text { when } x>2 \\ & -2 x-4, \text { if } \quad x \leq-2 \\ & 2 x+4, \quad \text { if } \quad-2<x \leq-2 / 3 \\ & =-4 x, \text { if } \quad-\frac{2}{3}<x \leq 0 \\ & 4 x, \quad \text { if } \quad 0<x \leq 2 \\ & 2 x+4, \quad \text { if } \quad x>2 \end{aligned} $
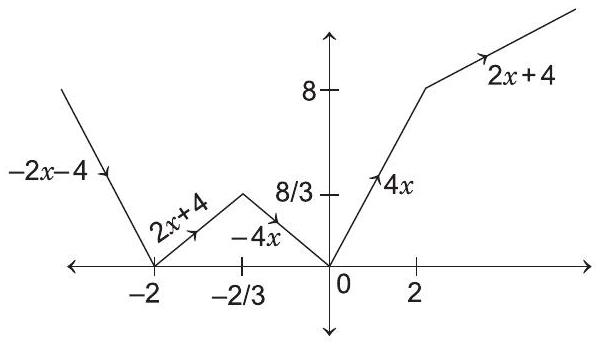
Graph for $y=f(x)$ is shown as
