Application of Derivatives 1 Question 10
####10. The normal to the curve $x^{2}+2 x y-3 y^{2}=0$ at $(1,1)$
(a) does not meet the curve again
(b) meets in the curve again the second quadrant
(c) meets the curve again in the third quadrant
(d) meets the curve again in the fourth quadrant
(2015 Main)
Show Answer
Answer:
Correct Answer: 10. $a=-\frac{1}{2}, b=-\frac{3}{4}, c=3$
Solution:
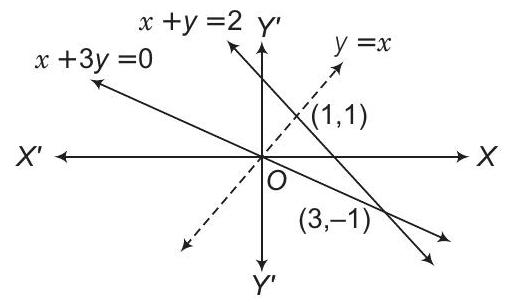
- Given equation of curve is
$ x^{2}+2 x y-3 y^{2}=0 $
On differentiating w.r.t $x$, we get
$ \begin{aligned} & 2 x+2 x y^{\prime}+2 y-6 y y^{\prime}=0 \Rightarrow y^{\prime}=\frac{x+y}{3 y-x} \\ & \text { At } \quad x=1, y=1, y^{\prime}=1 \\ & \text { i.e. } \quad \frac{d y}{d x}_{(1,1)}=1 \end{aligned} $
Equation of normal at $(1,1)$ is
$ \begin{aligned} y-1=-\frac{1}{1}(x-1) \Rightarrow & y-1=-(x-1) \\ \Rightarrow & x+y=2 \end{aligned} $
On solving Eqs. (i) and (ii) simultaneously, we get
$ \begin{array}{cc} \Rightarrow & x^{2}+2 x(2-x)-33(2-x)^{2}=0 \\ \Rightarrow & x^{2}+4 x-2 x^{2}-3\left(4+x^{2}-4 x\right)=0 \\ \Rightarrow & -x^{2}+4 x-12-3 x^{2}+12 x=0 \\ \Rightarrow & -4 x^{2}+16 x-12=0 \\ \Rightarrow & 4 x^{2}-16 x+12=0 \\ \Rightarrow & x^{2}-4 x+3=0 \\ \Rightarrow & (1-1)(x-3)=0 \\ \therefore & x=1,3 \end{array} $
Now, when $x=1$, then $y=1$
and when $x=3$, then $y=-1$
$ \therefore \quad P=(1,1) \text { and } Q=(3,-1) $
Hence, normal meets the curve again at $(3,-1)$ in fourth quadrant.
Alternate Solution
$ \begin{aligned} \text { Given, } & & x^{2}+2 x y-3 y^{2} & =0 \\ \Rightarrow & & (x-y)(x+3 y) & =0 \\ \Rightarrow & & x-y=0 \text { or } x+3 y & =0 \end{aligned} $
Equation of normal at $(1,1)$ is
$ y-1=-1(x-1) \Rightarrow x+y-2=0 $
It intersects $x+3 y=0$ at $(3,-1)$ and hence normal meets the curve in fourth quadrant.
