3D Geometry 3 Question 53
####53. Let $P_ {1}: 2 x+y-z=3$ and $P_ {2}: x+2 y+z=2$ be two planes. Then, which of the following statement(s) is (are) TRUE?
(2018 Adv.)
(a) The line of intersection of $P_ {1}$ and $P_ {2}$ has direction ratios $1,2,-1$
(b) The line $\frac{3 x-4}{9}=\frac{1-3 y}{9}=\frac{z}{3}$ is perpendicular to the line of intersection of $P_ {1}$ and $P_ {2}$
(c) The acute angle between $P_ {1}$ and $P_ {2}$ is $60^{\circ}$
(d) If $P_ {3}$ is the plane passing through the point $(4,2,-2)$ and perpendicular to the line of intersection of $P_ {1}$ and $P_ {2}$, then the distance of the point $(2,1,1)$ from the plane $P_ {3}$ is $\frac{2}{\sqrt{3}}$
Show Answer
Answer:
Correct Answer: 53. (c, d)
Solution:
- We have,
| $P_ {1}: 2 x+y-z=3$ | |
|---|---|
| and | $P_ {2}: x+2 y+z=2$ |
| Here, | $\vec{n}_ {1}=2 \hat{i}+\hat{j}-\hat{k}$ |
| and | $\vec{n}_ {2}=\hat{i}+2 \hat{j}+\hat{k}$ |
(a) Direction ratio of the line of intersection of $P_ {1}$
$ \begin{aligned} & \text { and } P_ {2} \text { is } \theta \vec{n}_ {1} \times \vec{n}_ {2} \end{aligned} $
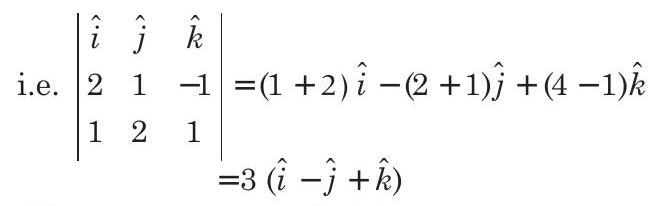
Hence, statement $a$ is false.
(b) We have, $\frac{3 x-4}{9}=\frac{1-3 y}{9}=\frac{z}{3}$
$ \Rightarrow \quad \frac{x-\frac{4}{3}}{3}=\frac{y-\frac{1}{3}}{-3}=\frac{z}{3} $
This line is parallel to the line of intersection of $P_ {1}$ and $P_ {2}$.
Hence, statement (b) is false.
(c) Let acute angle between $P_ {1}$ and $P_ {2}$ be $\theta$.
We know that,
$ \begin{aligned} \cos \theta=\frac{\overrightarrow{\mathbf{n}}_ {1} \cdot \overrightarrow{\mathbf{n}}_ {2}}{\left|\overrightarrow{\mathbf{n}}_ {1}\right|\left|\overrightarrow{\mathbf{n}}_ {2}\right|} & =\frac{(2 \hat{\mathbf{i}}+\hat{\mathbf{j}}-\hat{\mathbf{k}}) \cdot(\hat{\mathbf{i}}+2 \hat{\mathbf{j}}+\hat{\mathbf{k}})}{|2 \hat{\mathbf{i}}+\hat{\mathbf{j}}-\hat{\mathbf{k}}||\hat{\mathbf{i}}+2 \hat{\mathbf{j}}+\hat{\mathbf{k}}|} \\ & =\frac{2+2-1}{\sqrt{6} \times \sqrt{6}}=\frac{1}{2} \\ \theta & =60^{\circ} \end{aligned} $
Hence, statement (c) is true.
(d) Equation of plane passing through the point $(4,2,-2)$ and perpendicular to the line of intersection of $P_ {1}$ and $P_ {2}$ is
$ \begin{aligned} & & 3(x-4)-3(y-2)+3(z+2) & =0 \\ \Rightarrow & & 3 x-3 y+3 z-12+6+6 & =0 \\ \Rightarrow & & x-y+z & =0 \end{aligned} $
Now, distance of the point $(2,1,1)$ from the plane $x-y+z=0$ is
$D=\left|\frac{2-1+1}{\sqrt{1+1+1}}\right|=\frac{2}{\sqrt{3}}$
Hence, statement (d) is true.
