3D Geometry 3 Question 50
####50. Consider a pyramid $O P Q R S$ located in the first octant $(x \geq 0, y \geq 0, z \geq 0)$ with $O$ as origin, and $O P$ and $O R$ along the $X$-axis and the $Y$-axis, respectively. The base $O P Q R$ of the pyramid is a square with $O P=3$. The point $S$ is directly above the mid-point $T$ of diagonal $O Q$ such that $T S=3$. Then,
(2016 Adv.)
(a) the acute angle between $O Q$ and $O S$ is $\frac{\pi}{3}$
(b) the equation of the plane containing the $\triangle O Q S$ is $x-y=0$
(c) the length of the perpendicular from $P$ to the plane containing the $\triangle O Q S$ is $\frac{3}{\sqrt{2}}$
(d) the perpendicular distance from $O$ to the straight line containing $R S$ is $\sqrt{\frac{15}{2}}$
Show Answer
Answer:
Correct Answer: 50. (b, c, d)
Solution:
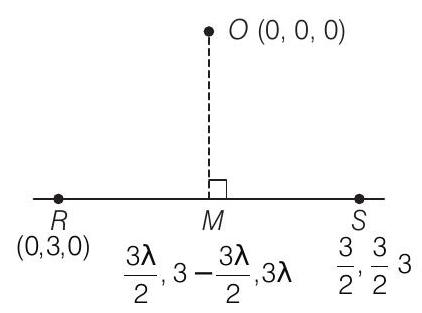
- Given, square base $O P=O R=3$
$\therefore$
Also, mid-point of $O Q$ is $T \frac{3}{2}, \frac{3}{2}, 0$.
Since, $S$ is directly above the mid-point $T$ of diagonal $O Q$ and $S T=3$. i.e. $\quad S \frac{3}{2}, \frac{3}{2}, 3$
Here, DR’s of $O Q(3,3,0)$ and DR’s of $O S \frac{3}{2}, \frac{3}{2}, 3$.
$\therefore \cos \theta=\frac{\frac{9}{2}+\frac{9}{2}}{\sqrt{9+9+0} \sqrt{\frac{9}{4}+\frac{9}{4}+9}}=\frac{9}{\sqrt{18} \cdot \sqrt{\frac{27}{2}}}=\frac{1}{\sqrt{3}}$
$\therefore$ Option (a) is incorrect.
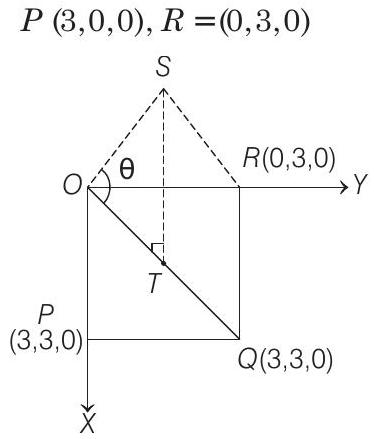
Now, equation of the plane containing the $\triangle O Q S$ is
$ \begin{aligned} & \quad\left|\begin{array}{ccc} x & y & z \\ 3 & 3 & 0 \\ 3 / 2 & 3 / 2 & 3 \end{array}\right|=0 \Rightarrow\left|\begin{array}{ccc} x & y & z \\ 1 & 1 & 0 \\ 1 & 1 & 2 \end{array}\right|=0 \\ & \Rightarrow \quad x(2-0)-y(2-0)+z(1-1)=0 \\ & \Rightarrow \quad \quad 2 x-2 y=0 \text { or } x-y=0 \\ & \therefore \text { Option (b) is correct. } \end{aligned} $
Now, length of the perpendicular from $P(3,0,0)$ to the plane containing $\triangle O Q S$ is $\frac{|3-0|}{\sqrt{1+1}}=\frac{3}{\sqrt{2}}$
$\therefore$ Option (c) is correct.
Here, equation of $R S$ is
$ \begin{array}{rlrl} \Rightarrow & \frac{x-0}{3 / 2} & =\frac{y-3}{-3 / 2}=\frac{z-0}{3}=\lambda \\ x & =\frac{3}{2} \lambda, y=-\frac{3}{2} \lambda+3, z=3 \lambda \end{array} $
To find the distance from $O(0,0,0)$ to $R S$.
Let $M$ be the foot of perpendicular.
$\because \quad \overline{O M} \perp \overline{R S} \Rightarrow \overline{O M} \cdot \overline{R S}=0$
$\Rightarrow \quad \frac{9 \lambda}{4}-\frac{3}{2} 3-\frac{3 \lambda}{2}+3(3 \lambda)=0 \Rightarrow \lambda=\frac{1}{3}$
$\therefore M \frac{1}{2}, \frac{5}{2}, 1 \Rightarrow O M=\sqrt{\frac{1}{4}+\frac{25}{4}+1}=\sqrt{\frac{30}{4}}=\sqrt{\frac{15}{2}}$
$\therefore$ Option (d) is correct.
