3D Geometry 3 Question 44
####44. Equation of the plane containing the straight line $\frac{x}{2}=\frac{y}{3}=\frac{z}{4}$ and perpendicular to the plane containing the staight lines $\frac{x}{3}=\frac{y}{4}=\frac{z}{2}$ and $\frac{x}{4}=\frac{y}{2}=\frac{z}{3}$ is
(2010)
(a) $x+2 y-2 z=0$
(b) $3 x+2 y-2 z=0$
(c) $x-2 y+z=0$
(d) $5 x+2 y-4 z=0$
Show Answer
Answer:
Correct Answer: 44. (c)
Solution:
- The DR’s of normal to the plane containing $\frac{x}{3}=\frac{y}{4}=\frac{z}{2}$ and $\frac{x}{4}=\frac{y}{z}=\frac{z}{3}$.
$ \mathbf{n}_{1}=\left|\begin{array}{ccc} \hat{\mathbf{i}} & \hat{\mathbf{j}} & \hat{\mathbf{k}} \\ 3 & 4 & 2 \\ 4 & 2 & 3 \end{array}\right|=(8 \hat{\mathbf{i}}-\hat{\mathbf{j}}-10 \hat{\mathbf{k}}) $
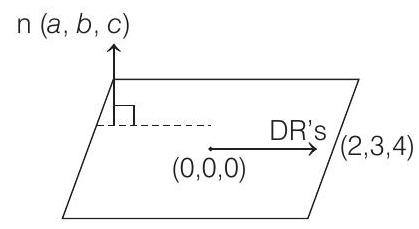
Also, equation of plane containing $\frac{x}{2}=\frac{y}{3}=\frac{z}{4}$ and DR’s of normal to be $\mathbf{n}_{1}=a \hat{\mathbf{i}}+b \hat{\mathbf{j}}+c \hat{\mathbf{k}}$
$\Rightarrow \quad a x+b y+c z=0$
where, $\mathbf{n}{1}: \mathbf{n}{2}=0$
$\Rightarrow \quad 8 a-b-10 c=0$
and $\mathbf{n}_{2} \perp(2 \hat{\mathbf{i}}+3 \hat{\mathbf{j}}+4 \hat{\mathbf{k}})$
$ \Rightarrow \quad 2 a+3 b+4 c=0 $
From Eqs (ii) and (iii),
$ \begin{aligned} \frac{a}{-4+30} & =\frac{b}{-20-32}=\frac{c}{24+2} \\ \Rightarrow \quad \frac{a}{26} & =\frac{b}{-52}=\frac{c}{26} \end{aligned} $
$ \Rightarrow \quad \frac{a}{1}=\frac{b}{-2}=\frac{c}{1} $
From Eqs. (i) and (iv), required equation of plane is $x-2 y+z=0$
