3D Geometry 3 Question 20
####20. The plane containing the line $\frac{x-3}{2}=\frac{y+2}{-1}=\frac{z-1}{3}$ and also containing its projection on the plane $2 x+3 y-z=5$, contains which one of the following points?
(2019 Main, 11 Jan I)
(a) $(-2,2,2)$
(b) $(2,2,0)$
(c) $(2,0,-2)$
(d) $(0,-2,2)$
Show Answer
Answer:
(c)
Solution:
- Let the direction vector of the line
$ \frac{x-3}{2}=\frac{y+2}{-1}=\frac{z-1}{3} \text { is } \mathbf{b}=2 \hat{\mathbf{i}}-\hat{\mathbf{j}}+3 \hat{\mathbf{k}} \text {. } $
Since, the required plane contains this line and its projection along the plane $2 x+3 y-z=5$, it will also contain the normal of the plane $2 x+3 y-z=5$.
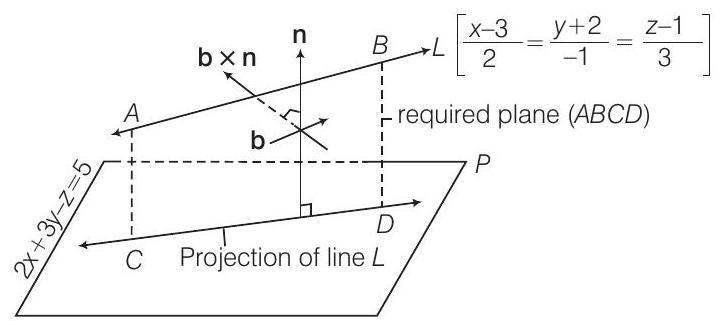
Normal vector of the plane $2 x+3 y-z=5$ is $\mathbf{n}=2 \hat{\mathbf{i}}+3 \hat{\mathbf{j}}-\hat{\mathbf{k}}$.
Now, the required plane contains $\mathbf{b}=2 \hat{\mathbf{i}}-\hat{\mathbf{j}}+3 \hat{\mathbf{k}}$ and $\mathbf{n}=2 \hat{\mathbf{i}}+3 \hat{\mathbf{j}}-\hat{\mathbf{k}}$.
$\therefore$ Normal of the required plane is $\mathbf{b} \times \mathbf{n}$.
Since, the plane contains the line $\frac{x-3}{2}=\frac{y+2}{-1}=\frac{z-1}{3}$, therefore it also contains the point $\mathbf{a}=3 \hat{\mathbf{i}}-2 \hat{\mathbf{j}}+\hat{\mathbf{k}}$.
Now, the equation of required plane is $(\mathbf{r}-\mathbf{a}) \cdot(\mathbf{b} \times \mathbf{n})=0$
$ \left|\begin{array}{ccc} x-3 & y+2 & z-1 \\ 2 & -1 & 3 \\ 2 & 3 & -1 \end{array}\right|=0 $
$\Rightarrow(x-3)[1-9]-(y+2)[-2-6]+(z-1)[6+2]=0$
$\Rightarrow-8 x+8 y+8 z+32=0$
$\Rightarrow x-y-z=4$
Note that $(2,0,-2)$ is the only point which satisfy above equation.
