3D Geometry 3 Question 19
####19. If the point $(2, \alpha, \beta)$ lies on the plane which passes through the points $(3,4,2)$ and
$(7,0,6)$ and is perpendicular to the plane $2 x-5 y=15$, then $2 \alpha-3 \beta$ is equal to
(2019 Main, 11 Jan II)
(a) 17
(b) 7
(c) 5
(d) 12
Show Answer
Answer:
(b)
Solution:
- According to given information, we have the following figure.
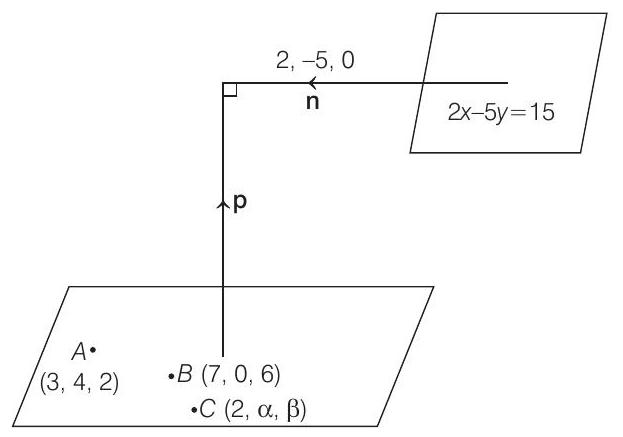
From figure, it is clear that
$(\mathbf{A B} \times \mathbf{B C})=\mathbf{p}$ and $\mathbf{n}=2 \hat{\mathbf{i}}-5 \hat{\mathbf{j}}+0 \hat{\mathbf{k}}$
$ \therefore \mathbf{p}=\left|\begin{array}{ccc} \hat{\mathbf{i}} & \hat{\mathbf{j}} & \hat{\mathbf{k}} \\ 4 & -4 & 4 \\ -5 & \alpha & \beta-6 \end{array}\right| $
$[\because \mathbf{A B}=(7-3) \hat{\mathbf{i}}+(0-4) \hat{\mathbf{j}}+(6-2) \hat{\mathbf{k}}$
$=4 \hat{\mathbf{i}}-4 \hat{\mathbf{j}}+4 \hat{\mathbf{k}}$ and $\mathbf{B C}=(2-7) \hat{\mathbf{i}}+(\alpha-0) \hat{\mathbf{j}}+(\beta-6) \hat{\mathbf{k}}$
$=-5 \hat{\mathbf{i}}+\alpha \hat{\mathbf{j}}+(\beta-6) \hat{\mathbf{k}}]$
$=\hat{\mathbf{i}}(-4 \beta+24-4 \alpha)-\hat{\mathbf{j}}(4 \beta-24+20)+\hat{\mathbf{k}}(4 \alpha-20)$
$\Rightarrow \mathbf{p}=(24-4 \alpha-4 \beta) \hat{\mathbf{i}}+\hat{\mathbf{j}}(4-4 \beta)+\hat{\mathbf{k}}(4 \alpha-20)$
Now, as the planes are perpendicular, therefore $\mathbf{p} \cdot \mathbf{n}=0$
$\Rightarrow((24-4 \alpha-4 \beta) \hat{\mathbf{i}}+(4-4 \beta) \hat{\mathbf{j}}+(4 \alpha-20) \hat{\mathbf{k}})$
$ \cdot(2 \hat{\mathbf{i}}-5 \hat{\mathbf{j}}+0 \hat{\mathbf{k}}))=0 $
$\Rightarrow 2(24-4 \alpha-4 \beta)-5(4-4 \beta)+0=0$
$\Rightarrow 8(6-\alpha-\beta)-4(5-5 \beta)=0$
$\Rightarrow \quad 12-2 \alpha-2 \beta-5+5 \beta=0 \Rightarrow 2 \alpha-3 \beta=7$
