States of Matter - Result Question 47
####47. A closed tank has two compartments $A$ and $B$, both filled with oxygen (assumed to be ideal gas). The partition separating the two compartments is fixed and is a perfect heat insulator (Fig. 1). If the old partition is replaced by a new partition which can slide and conduct heat but does not allow the gas to leak across (Fig. 2), the volume (in $m^{3}$ ) of the compartment $A$ after the system attains equilibrium is
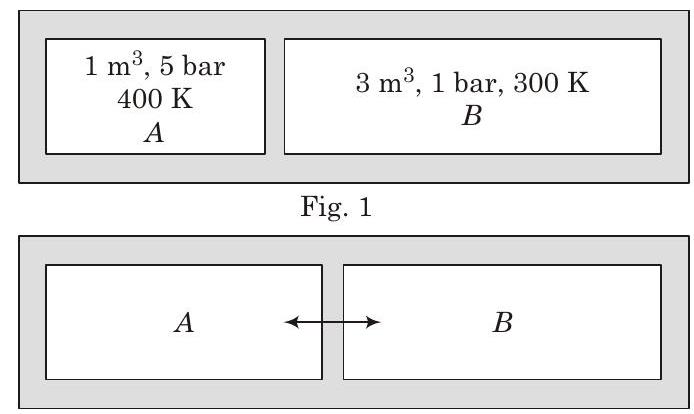
Fig. 2
(2018 Adv)
Assertion and Reason
Read the following questions and answer as per the direction given below :
(a) Statement I is correct; Statement II is correct; Statement II is the correct explanation of Statement I
(b) Statement I is correct; Statement II is correct; Statement II is not the correct explanation of Statement I
(c) Statement I is correct; Statement II is incorrect
(d) Statement I is incorrect; Statement II is correct
Show Answer
Solution:
- Given $p _1=5$ bar, $V _1=1 m^{3}, T _1=400 K$
So, $\quad n _1=\frac{5}{400 R}$
(from $p V=n R T$ )
Similarly, $p _2=1$ bar, $V _2=3 m^{3}, T _2=300 K, n _2=\frac{3}{300 R}$
Let at equilibrium the new volume of $A$ will be $(1+x)$
So, the new volume of $B$ will be $(3-x)$
Now, from the ideal gas equation.
$$ \frac{p _1 V _1}{n _1 R T _1}=\frac{p _2 V _2}{n _2 R T _2} $$
and at equilibrium (due to conduction of heat)
$$ \begin{aligned} \frac{p _1}{T _1} & =\frac{p _2}{T _2} \ \text { So, } \quad \frac{V _1}{n _1} & =\frac{V _2}{n _2} \text { or } V _1 n _2=V _2 n _1 \end{aligned} $$
After putting the values
$$ \begin{aligned} & (1+x) \times \frac{3}{300 R}=(3-x) \times \frac{5}{400 R} \text { or }(1+x)=\frac{(3-x) 5}{4} \ & \text { or } 4(1+x)=15-5 x \text { or } 4+4 x=15-5 x \text { or } x=\frac{11}{9} \end{aligned} $$
Hence, new volume of $A$ i.e., $(1+x)$ will comes as $1+\frac{11}{9}=\frac{20}{9}$ or 2.22






