Solid State - Result Question 29
####29. Consider an ionic solid
(2018 Adv.)
(a) Remove all the anions
(b) Replace all the face centered cations
(c) Remove all the corner cations
(d) Replace the central anion
The value of
Show Answer
Answer:
Correct Answer: 29. (3)
Solution:
- The unit cell of initial structure of ionic solid
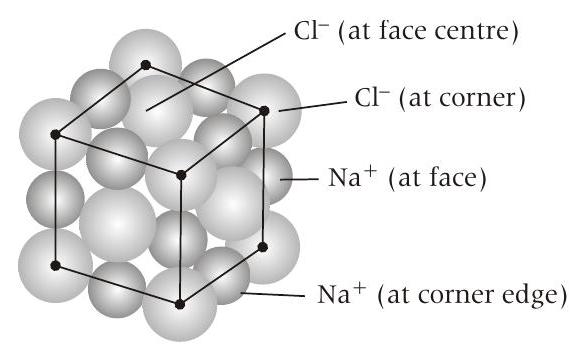
In
However, as per the demand of problem the position of cations and anions are swapped.
We also know that (for 1 unit cell)
(A) Total number of atoms at
(B) Total number of octahedral voids
(as no. of atoms at
Now taking the conditions one by one
(i) If we remove all the anions except the central one than number of left anions.
(ii) If we replace all the face centred cations by anions than effective number of cations will be
Likewise effective number of anions will be
(iii) If we remove all the corner cations then effective number of cations will be
(iv) If we replace central anion with cation then effective number of cations will be
Likewise effective number of anions will be
Thus, as the final outcome, total number of cations present in
Likewise, total number of anions
Hence, the value of






