Solid State - Result Question 25
####25. The correct statement(s) for cubic close packed (ccp) three dimensional structure is (are)
(2016 Adv.)
(a) The number of the nearest neighbours of an atom present in the topmost layer is 12
(b) The packing efficiency of atom is $74 \text{\%}$
(c) The number of octahedral and tetrahedral voids per atom are 1 and 2 , respectively
(d) The unit cell edge length is $2 \sqrt{2}$ times the radius of the atom
Show Answer
Answer:
Correct Answer: 25. $(b, c, d)$
Solution:
- (a) Nearest neighbour in the topmost layer of ccp structure is 9 thus, incorrect.
(b) Packing efficiency is $74 \text{\%}$ thus, correct.
(c) Tetrahedral voids $=2$
Octahedral voids $=1$ per atom thus, correct.
(d) Edge length, $a=\frac{4}{\sqrt{2}} r=2 \sqrt{2} r$
thus, correct
Explanation Edge length $=a$
Radius $=r$
$$ \begin{aligned} A C^{2} & =A B^{2}+B C^{2} \\ (4 r)^{2} & =a^{2}+a^{2}=2 a^{2} \\ 4 r & =\sqrt{2} a \\ \Rightarrow \quad r & =\frac{\sqrt{2}}{4} a=\frac{a}{2 \sqrt{2}} \Rightarrow a=2 \sqrt{2} r \end{aligned} $$
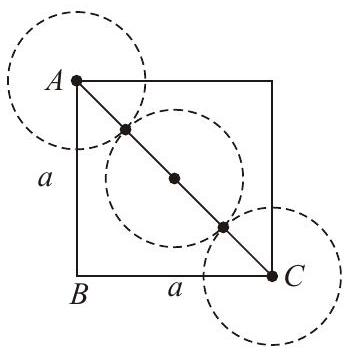
In ccp structure, number of spheres is 4 .
Hence, volume of 4 spheres $=4\left(\frac{4}{3} \pi r^{3}\right)$
Total volume of unit cell $=a^{3}=(2 \sqrt{2} r)^{3}$
$\text{\%}$ of packing efficiency
$$ \begin{aligned} & =\frac{\text { Volume of } 4 \text { spheres }}{\text { Volume of unit cell }}=\frac{4\left(\frac{4}{3} \pi r^{3}\right)}{[2(\sqrt{2} r)]^{3}} \times 100 \\ & =74.05 \text{\%} \simeq 74 \text{\%} \end{aligned} $$






