Chemical and Ionic Equilibrium - Result Question 28
####28. For a reaction, $A \rightleftharpoons P$, the plots of $[A]$ and $[P]$ with time at temperatures $T _1$ and $T _2$ are given below.
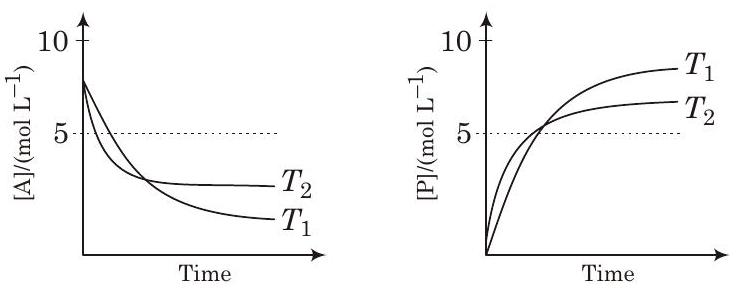
If $T _2>T _1$, the correct statement(s) is are
(Assume $\Delta H^{\ominus}$ and $\Delta S^{\ominus}$ are independent of temperature and ratio of $\ln K$ at $T _1$ to $\ln K$ at $T _2$ is greater than $T _2 / T _1$. Here $H, S, G$ and $K$ are enthalpy, entropy, Gibbs energy and equilibrium constant, respectively.)
(2018 Adv.)
(a) $\Delta H^{\ominus}<0, \Delta S^{\ominus}<0$
(b) $\Delta G^{\ominus}<0, \Delta H^{\ominus}>0$
(c) $\Delta G^{\ominus}<0, \Delta S^{\ominus}<0$
(d) $\Delta G^{\ominus}<0, \Delta S^{\ominus}>0$
Show Answer
Solution:
- For the reaction, $A \rightleftharpoons P$
Given,
$$ \begin{array}{r} T _1<T _2 \ \frac{\ln K _1}{\ln K _2}>\frac{T _2}{T _1} \end{array} $$
It shows, On increasing the temperature, $K$ decreases so reaction is exothermic i.e., $\Delta H^{\circ}<0$
Besides, graph shows $K>1$
So
$$ \Delta G^{o}<0 $$
Now from equation (i)
$$ \begin{array}{ll} & T _1 \ln K _1>T _2 \ln K _2 \ & -\Delta G^{o}>-\Delta G^{o} \ \text { Likewise } & \left(-\Delta H^{o}+T _1 \Delta S^{o}\right)>\left(-\Delta H^{o}+T _2 \Delta S^{o}\right) \ \text { or simply } & T _1 \Delta S^{o}>T _2 \Delta S^{o} \ \text { So, } & \left(T _2-T _1\right) \Delta S^{\circ}<0 \ \therefore & \Delta S^{o}<0 \end{array} $$
In other words, increase of $\Delta G$ with increase in temperature is possible only when $\Delta S^{\circ}<0$. Hence, options (a) and (c) are correct.






