Chapter 8

APPLICATION OF INTEGRALS

8.1 Overview

This chapter deals with a specific application of integrals to find the area under simple curves, area between lines and arcs of circles, parabolas and ellipses, and finding the area bounded by the above said curves.

8.1.1 The area of the region bounded by the curve $y=f(x), x$-axis and the lines $x=a$ and $x=b(b>a)$ is given by the formula:

$ \text{ Area }=\int_a^{b} y d x \ = \ \int_a^{b} f(x) d x $

8.1.2 The area of the region bounded by the curve $x=\phi(y), y$-axis and the lines $y=c, \ y=d$ is given by the formula:

$ \text{ Area }=\int_c^{d} x d y=\int_c^{d} \phi(y) d y $

8.1.3 The area of the region enclosed between two curves $y=f(x), y=g(x)$ and the lines $x=a, x=b$ is given by the formula.

$ \text{ Area }=\int_a^{b}[f(x)-g(x)] d x \text{, where } f(x) \geq g(x) \text{ in }[a, b] $

8.1.4 If $f(x) \geq g(x)$ in $[a, c]$ and $f(x) \leq g(x)$ in $[c, b], a<c<b$, then

Area $=\int_a^{c}[f(x)-g(x)] d x+\int_c^{b}(g(x)-f(x)) d x$

8.2 Solved Examples

Short Answer (S.A.)

Example 1 Find the area of the curve $y=\sin x$ between 0 and $\pi$.

Solution We have

$ \begin{aligned} \text{ Area } OAB & =\int_0^{\pi} y d x=\int_0^{\pi} \sin x d x=|-\cos x|_0^{\pi} \\ & =\cos 0-\cos \pi=2 \text{ sq units. } \end{aligned} $

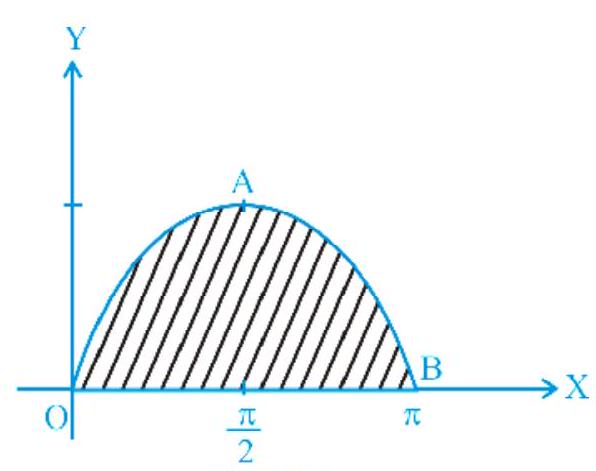Fig. 8.1

Example 2 Find the area of the region bounded by the curve $a y^{2}=x^{3}$, the $y$-axis and the lines $y=a$ and $y=2 a$.

Solution We have

$ \begin{aligned} \text{ Area BMNC }=\int_a^{2 a} x d y & =\int_a^{2 a} a^{\frac{1}{3}} y^{\frac{2}{3}} d y \\ & =\frac{3 a^{\frac{1}{3}}}{5}\big|y^{\frac{5}{3}}\big|_a^{2 a} \\ & =\frac{3 a^{\frac{1}{3}}}{5}\big|(2 a)^{\frac{5}{3}}-a^{\frac{5}{3}}\big| \\ & =\frac{3}{5} a^{\frac{1}{3}} a^{\frac{5}{3}}\big|(2)^{\frac{5}{3}}-1\big| \\ & =\frac{3}{5} a^{2}\big|2.2^{\frac{2}{3}}-1\big| \text{ sq units. } \end{aligned} $

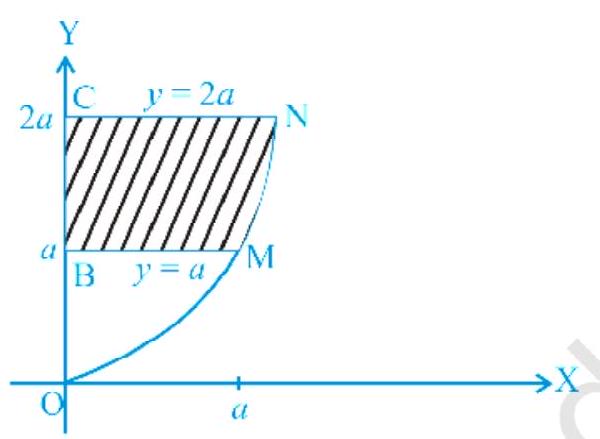Fig. 8.2

Example 3 Find the area of the region bounded by the parabola $y^2 = 2x $ and the straight line $x-y = 4$

Solution The intersecting points of the given curves are obtained by solving the equations

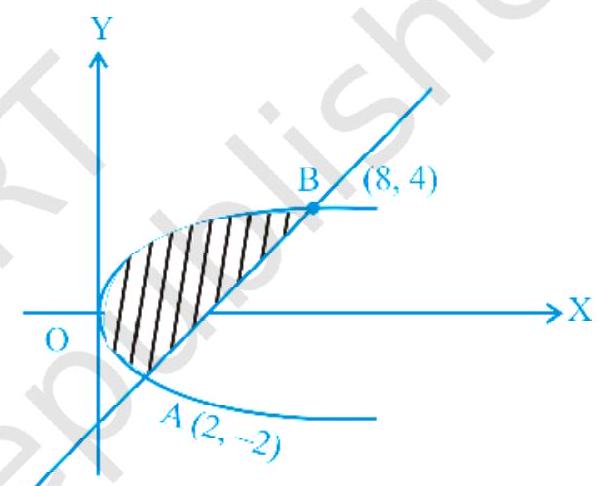Fig. 8.3

$x-y=4$ and $y^{2}=2 x$ for $x$ and $y$.

We have $y^{2}=8+2 y$ i.e., $(y-4)(y+2)=0$

which gives $y=4,-2$ and

$x=8,2$.

Thus, the points of intersection are

$(8,4),(2,-2)$. Hence

Area $=\int _{-2}^{4} \big(4+y-\frac{1}{2} y^{2}\big) d y$

$=\Big|4 y+\frac{y^{2}}{2}-\frac{1}{6} y^{3}\Big| _{-2}^{4}=18$ sq units.

Example 4 Find the area of the region bounded by the parabolas $y^{2}=6 x$ and $x^{2}=6 y$.

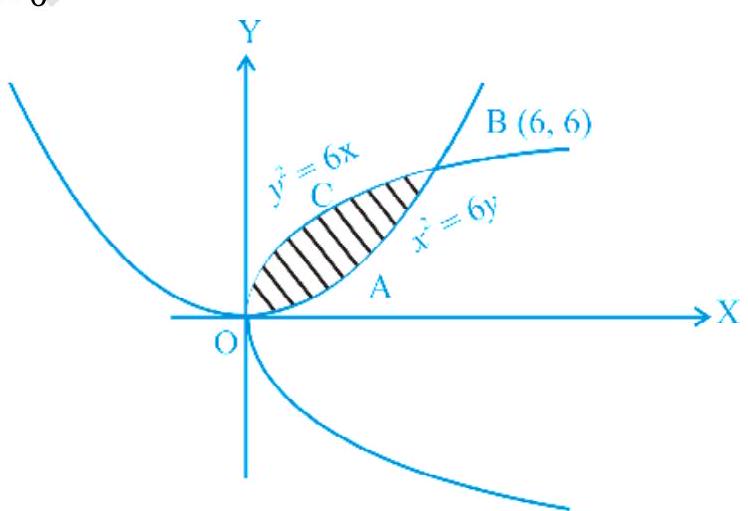Fig. 8.4

Solution The intersecting points of the given parabolas are obtained by solving these equations for $x$ and $y$, which are $0(0,0)$ and $(6,6)$. Hence

Area $OABC \ =\int_0^{6} \big(\sqrt{6 x}-\frac{x^{2}}{6}\big)d x=\bigg|2 \sqrt{6} \frac{x^{\frac{3}{2}}}{3}-\frac{x^{3}}{18}\bigg|_0^{6}$

$=2 \sqrt{6} \frac{(6)^{\frac{3}{2}}}{3}-\frac{(6)^{3}}{18}=12$ sq units.

Example 5 Find the area enclosed by the curve $x=3 cost, y=2 \sin t$.

Solution Eliminating $t$ as follows:

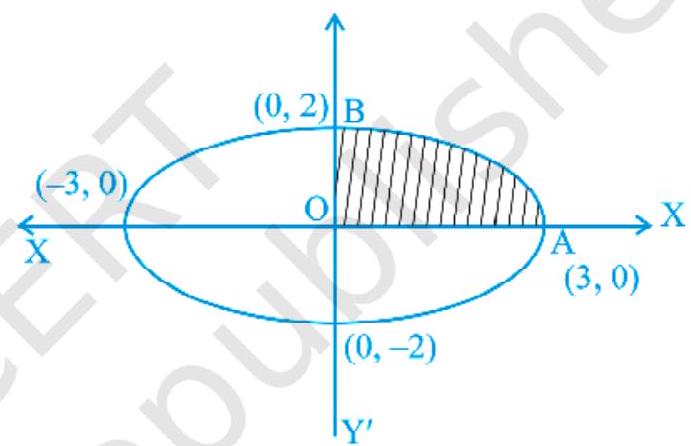Fig. 8.5

$x=3 \ \cos t, y=2 \ \sin t \Rightarrow \frac{x}{3}=\cos t$,

$\frac{y}{2}=\sin t$, we obtain

$\frac{x^{2}}{9}+\frac{y^{2}}{4}=1$,

which is the equation of an ellipse. From Fig. 8.5, we get

the required area $=4 \int_0^{3} \frac{2}{3} \sqrt{9-x^{2}} d x$

$=\frac{8}{3} \big[\frac{x}{2} \sqrt{9-x^{2}}+\frac{9}{2} \sin ^{-1} \frac{x}{3}\big]_0^3 =6 \pi$ sq units.

Long Answer (L.A.)

Example 6 Find the area of the region included between the parabola $y=\frac{3 x^{2}}{4}$ and the line $3 x-2 y+12=0$.

Solution Solving the equations of the given curves $y=\frac{3 x^{2}}{4}$ and $3 x-2 y+12=0$,

we get

$3 x^{2}-6 x-24=0 \quad \Rightarrow \quad(x-4)(x+2)=0$

$\Rightarrow x=4, x=-2$ which give

$y=12, y=3$

From Fig.8.6, the required area $=$ area of ABC

$=\int _{-2}^{4} \Big(\frac{12+3 x}{2}\Big) d x-\int _{-2}^{4} \frac{3 x^{2}}{4} d x$

$= \Big(6 x+{\frac{3 x^{2}}{4}}\Big)_{-2}^{4}-\big|\frac{3 x^{3}}{12}\Big| _{-2}^{4}=27$ sq units.

Example 7 Find the area of the region bounded by the curves $x=a t^{2}$ and $y=2 a t$ between the ordinate coresponding to $t=1$ and $t=2$.

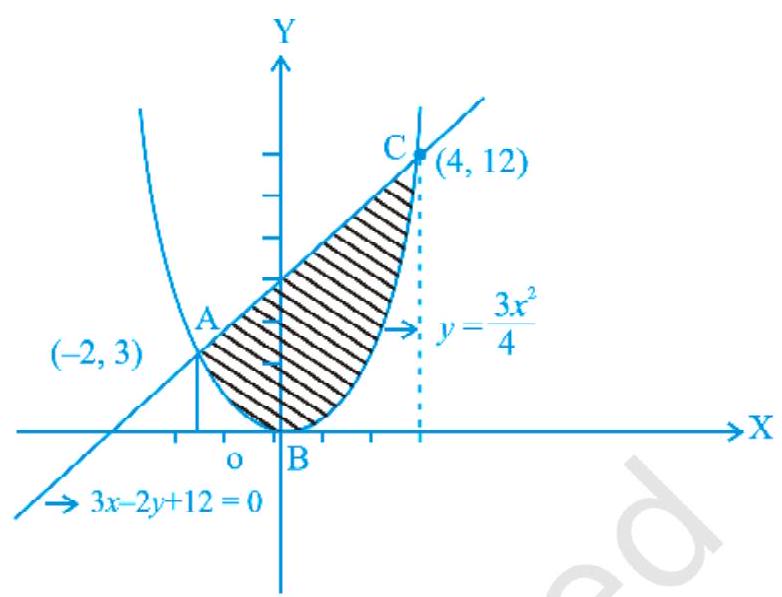Fig. 8.6

Solution Given that $x=a t^{2} \quad \ldots(i)$,

$y=2 a t \ldots$ (ii) $\Rightarrow t=\frac{y}{2 a}$ putting the value of $t$ in (i), we get $y^{2}=4 a x$ Putting $t=1$ and $t=2$ in (i), we get $x=a$, and $x=4 a$

Required area $=2$ area of $ABCD=$

$2 \int_a^{4 a} y d x=2 \times 2 \int_a^{4 a} \sqrt{a x} d x$

$=8 \sqrt{a}\Big|\frac{(x)^{\frac{3}{2}}}{3}\Big|_a^{4 a}=\frac{56}{3} a^{2}$ sq units.

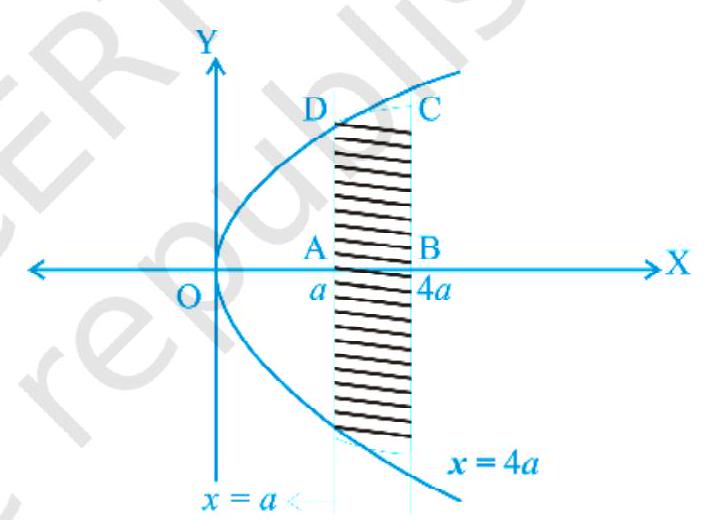Fig. 8.7

Example 8 Find the area of the region above the $x$-axis, included between the parabola $y^{2}=a x$ and the circle $x^{2}+y^{2}=2 a x$.

Solution Solving the given equations of curves, we have

$ x^{2}+a x=2 a x $

or $x=0, x=a$, which give

$y=0 . \quad \quad y= \pm a$

From Fig. 8.8 area $ODAB=$

$\int_0^{a}\big(\sqrt{2 a x-x^{2}}-\sqrt{a x}\big) d x$

Let $x=2 a \sin ^{2} \theta$. Then $d x=4 a$ $\sin \theta \cos \theta d \theta$ and

$x=0, \Rightarrow \theta=0, x=a \Rightarrow \theta=\frac{\pi}{4}$.

Again, $\int_0^{a} \sqrt{2 a x–x^{2}} d x$

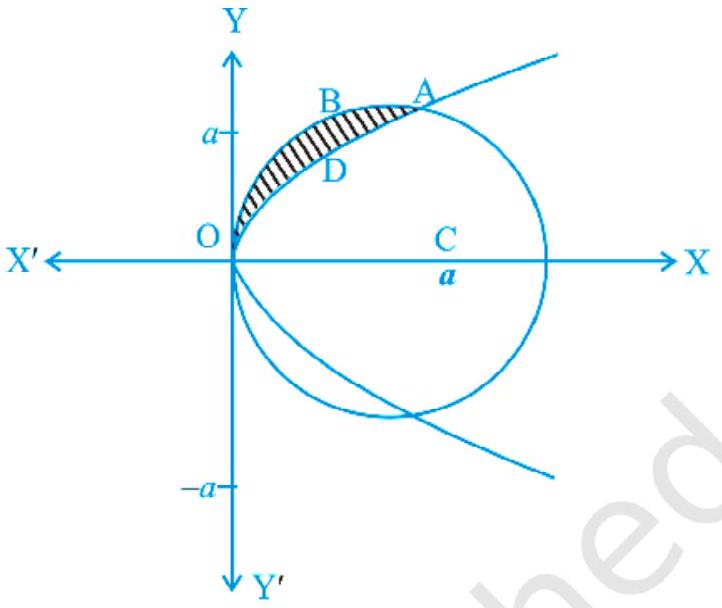Fig. 8.8

$=\int_0^{\frac{\pi}{4}}(2 a \sin \theta \cos \theta)(4 a \sin \theta \cos \theta) d \theta$

$=a^{2} \int_0^{\frac{\pi}{4}}(1-\cos 4 \theta) d \theta=a^{2} \big(\theta-\frac{\sin 4 \theta}{4}\big)_0^{\frac{\pi}{4}}=\frac{\pi}{4} a^{2}$.

Further more,

$ \int_0^{a} \sqrt{a x} d x=\sqrt{a} \frac{2}{3} \Big(x^{\frac{3}{2}}\Big)_0^{a}=\frac{2}{3} a^{2} $

Thus the required area $=\frac{\pi}{4} a^{2}-\frac{2}{3} a^{2}=a^{2} \quad \big(\frac{\pi}{4}-\frac{2}{3}\big)$ sq units.

Example 9 Find the area of a minor segment of the circle $x^{2}+y^{2}=a^{2}$ cut off by the line $x=\frac{a}{2}$.

Solution Solving the equation $x^{2}+y^{2}=a^{2}$ and $x=\frac{a}{2}$, we obtain their points of intersection which are $\Big(\frac{a}{2}, \sqrt{3} \frac{a}{2}\Big)$ and $\Big(\frac{a}{2},-\frac{\sqrt{3} a}{2}\Big)$.

Hence, from Fig. 8.9, we get

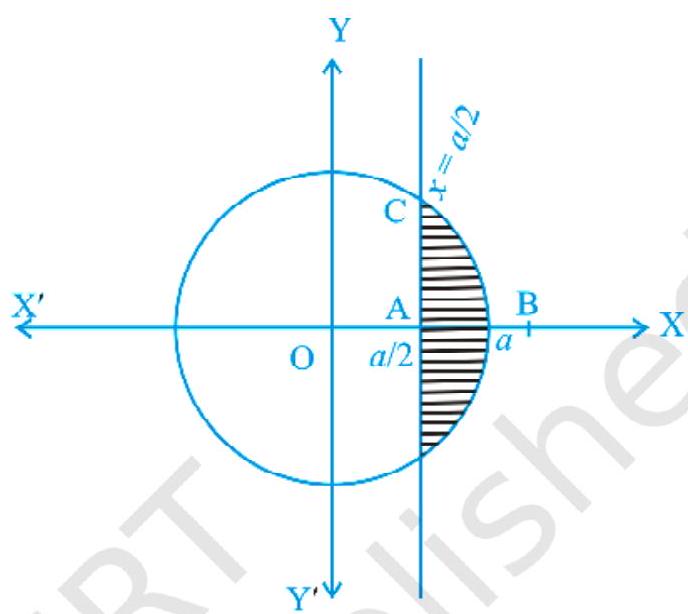Fig. 8.9

Required Area $=2$ Area of $OAB=2 \int _{\frac{a}{2}}^{a} \sqrt{a^{2}-x^{2}} d x$

$=2 \Big[\frac{x}{2} \sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2} \sin ^{-1} \frac{x}{a}\Big]_{\frac{a}{2}}^{a}$

$=2 \Big[\frac{a^{2}}{2} \cdot \frac{\pi}{2}-\frac{a}{4} \cdot a \frac{\sqrt{3}}{2}-\frac{a^{2}}{2} \cdot \frac{\pi}{6}\Big]$

$=\frac{a^{2}}{12}\big(6 \pi-3 \sqrt{3}-2 \pi \big)$

$=\frac{a^{2}}{12}\big(4 \pi-3 \sqrt{3}\big)$ sq units.

Objective Type Questions

Choose the correct answer from the given four options in each of the Examples 10 to 12.

Example 10 The area enclosed by the circle $x^{2}+y^{2}=2$ is equal to

(A) $4 \pi$ sq units

(B) $2 \sqrt{2} \pi$ sq units

(C) $4 \pi^{2}$ sq units

(D) $2 \pi$ sq units

Solution Correct answer is (D); since Area $=4 \int_0^{\sqrt{2}} \sqrt{2-x^{2}}$

$ =4 \big(\frac{x}{2} \sqrt{2-x^{2}}+\sin ^{-1} \frac{x}{\sqrt{2}}\big)_0^{\sqrt{2}}=2 \pi \text{ sq. units. } $

Example 11 The area enclosed by the ellipse $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ is equal to

(A) $\pi^{2} a b$

(B) пab

(C) $\pi a^{2} b$

(D) $\pi a b^{2}$

Solution Correct answer is (B); since Area $=4 \int_0^{a} \frac{b}{a} \sqrt{a^{2}-x^{2}} d x$

$ =\frac{4 b}{a} \Big[\frac{x}{2} \sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2} \sin ^{-1} \frac{x}{a}\Big]_0^{a}=\pi a b . $

Example 12 The area of the region bounded by the curve $y=x^{2}$ and the line $y=16$

(A) $\frac{32}{3}$ 、

(B) $\frac{256}{3}$

(C) $\frac{64}{3}$

(D) $\frac{128}{3}$

Solution Correct answer is (B); since Area $=2 \int_0^{16} \sqrt{y} d y$

Fill in the blanks in each of the Examples 13 and 14.

Example 13 The area of the region bounded by the curve $x=y^{2}, y$-axis and the line $y=3$ and $y=4$ is____________

Solution $\frac{37}{3}$ sq. units

Example 14 The area of the region bounded by the curve $y=x^{2}+x, x$-axis and the line $x=2$ and $x=5$ is equal to________________.

Solution $\frac{297}{6}$ sq. units

8.3 EXERCISES

Short Answer (S.A.)

1. Find the area of the region bounded by the curves $y^{2}=9 x, y=3 x$.

2. Find the area of the region bounded by the parabola $y^{2}=2 p x, x^{2}=2 p y$.

3. Find the area of the region bounded by the curve $y=x^{3}$ and $y=x+6$ and $x=0$.

4. Find the area of the region bounded by the curve $y^{2}=4 x, x^{2}=4 y$.

5. Find the area of the region included between $y^{2}=9 x$ and $y=x$

6. Find the area of the region enclosed by the parabola $x^{2}=y$ and the line $y=x+2$

7. Find the area of region bounded by the line $x=2$ and the parabola $y^{2}=8 x$

8. Sketch the region $\lbrace (x, 0): y=\sqrt{4-x^{2}} \rbrace$ and $x$-axis. Find the area of the region using integration.

9. Calcualte the area under the curve $y=2 \sqrt{x}$ included between the lines $x=0$ and $x=1$.

10. Using integration, find the area of the region bounded by the line $2 y=5 x+7, x$ axis and the lines $x=2$ and $x=8$.

11. Draw a rough sketch of the curve $y=\sqrt{x-1}$ in the interval $[1,5]$. Find the area under the curve and between the lines $x=1$ and $x=5$.

12. Determine the area under the curve $y=\sqrt{a^{2}-x^{2}}$ included between the lines $x$ $=0$ and $x=a$.

13. Find the area of the region bounded by $y=\sqrt{x}$ and $y=x$.

14. Find the area enclosed by the curve $y=-x^{2}$ and the straight lilne $x+y+2=0$.

15. Find the area bounded by the curve $y=\sqrt{x}, x=2 y+3$ in the first quadrant and $x$-axis

Long Answer (L.A.)

16. Find the area of the region bounded by the curve $y^{2}=2 x$ and $x^{2}+y^{2}=4 x$.

17. Find the area bounded by the curve $y=\sin x$ between $x=0$ and $x=2 \pi$.

18. Find the area of region bounded by the triangle whose vertices are $(-1,1),(0$, $5)$ and ( 3,2 ), using integration.

19. Draw a rough sketch of the region $ \lbrace(x, y): y^{2} \leq 6 a x.$ and $.x^{2}+y^{2} \leq 16 a^{2} \rbrace$. Also find the area of the region sketched using method of integration.

20. Compute the area bounded by the lines $x+2 y=2, y-x=1$ and $2 x+y=7$.

21. Find the area bounded by the lines $y=4 x+5, y=5-x$ and $4 y=x+5$.

22. Find the area bounded by the curve $y=2 \cos x$ and the $x$-axis from $x=0$ to $x=2 \pi$.

23. Draw a rough sketch of the given curve $y=1+|x+1|, x=-3, x=3, y=0$ and find the area of the region bounded by them, using integration.

Objective Type Questions

Choose the correct answer from the given four options in each of the Exercises 24 to 34 .

24. The area of the region bounded by the $y$-axis, $y=\cos x$ and $y=\sin x, 0 \leq x \leq \frac{\pi}{2}$ is

(A) $\sqrt{2}$ sq units

(B) $(\sqrt{2}+1)$ sq units

(C) $(\sqrt{2}-1)$ sq units

(D) $(2 \sqrt{2}-1)$ sq units

25. The area of the region bounded by the curve $x^{2}=4 y$ and the straight line $x=4 y-2$ is

(A) $\frac{3}{8}$ sq units

(B) $\frac{5}{8}$ sq units

(C) $\frac{7}{8}$ sq units

(D) $\frac{9}{8}$ sq units

26. The area of the region bounded by the curve $y=\sqrt{16-x^{2}}$ and $x$-axis is

(A) 8 sq units

(B) $20 \pi s q$ units

(C) $16 \pi$ sq units

(D) $256 \pi$ sq units

27. Area of the region in the first quadrant enclosed by the $x$-axis, the line $y=x$ and the circle $x^{2}+y^{2}=32$ is

(A) $16 \pi$ sq units

(B) $4 \pi$ sq units

(C) $32 \pi$ sq units

(D) 24 sq units

28. Area of the region bounded by the curve $y=\cos x$ between $x=0$ and $x=\pi$ is

(A) 2 sq units

(B) 4 sq units

(C) 3 sq units

(D) 1 sq units

29. The area of the region bounded by parabola $y^{2}=x$ and the straight line $2 y=x$ is

(A) $\frac{4}{3}$ sq units

(B) 1 sq units

(C) $\frac{2}{3}$ sq units

(D) $\frac{1}{3}$ sq units

30. The area of the region bounded by the curve $y=\sin x$ between the ordinates $x=0, x=\frac{\pi}{2}$ and the $x$-axis is

(A) 2 sq units

(B) 4 sq units

(C) 3 sq units

(D) 1 sq units

31. The area of the region bounded by the ellipse $\frac{x^{2}}{25}+\frac{y^{2}}{16}=1$ is

(A) $20 \pi$ sq units

(C) $16 \pi^{2}$ sq units

(B) $20 \pi^{2}$ sq units

(D) $25 \pi$ sq units

32. The area of the region bounded by the circle $x^{2}+y^{2}=1$ is

(A) $2 \pi$ sq units

(B) $\pi$ sq units

(C) $3 \pi$ sq units

(D) $4 \pi$ sq units

33. The area of the region bounded by the curve $y=x+1$ and the lines $x=2$ and $x=3$ is

(A) $\frac{7}{2}$ sq units

(B) $\frac{9}{2}$ sq units

(C) $\frac{11}{2}$ sq units

(D) $\frac{13}{2}$ sq units

34. The area of the region bounded by the curve $x=2 y+3$ and the $y$ lines. $y=1$ and $y=-1$ is

(A) 4 sq units

(B) $\frac{3}{2}$ sq units

(C) 6 sq units

(D) 8 sq units

SOLUTIONS

1. $\frac{1}{2}$ sq.units

2. $\frac{4}{3} p^{2}$ sq. units

3. 10 sq.units

4. $\frac{16}{3}$ sq.units

5. $\frac{27}{2}$ sq.units

6. $\frac{9}{2}$ sq. units

7. $\frac{32}{3}$ sq. units

8. $2 \pi$ sq.units

9. $\frac{4}{3}$ sq.units

10. 96 sq.units

11. $\frac{16}{3}$ sq.units

12. $\frac{\pi a^{2}}{4}$ sq. units

13. $\frac{1}{6}$ sq. units

14. $\frac{9}{2}$ sq. units

15. 9 sq.units

16. $2 \Big[\pi-\frac{8}{3}\Big]$ sq.units

17. 4 sq.units

18. $\frac{15}{2}$ sq. units

19. $\frac{4}{3}(\sqrt{3}+2 \pi) a^{2}$ sq. units

20. 6 sq.units

21. $\frac{15}{2}$ sq. units

22. 8 sq.units

23. 15 sq.units

24. C

25. D

26. A

27. B

28. A

29. A

30. D

31. A

32. B

33. A

34. C