Conic Sections
Short Answer Type Questions
1. Find the equation of the circle which touches the both axes in first quadrant and whose radius is
Show Answer
Solution
Given that radius of the circle is a i.e.,
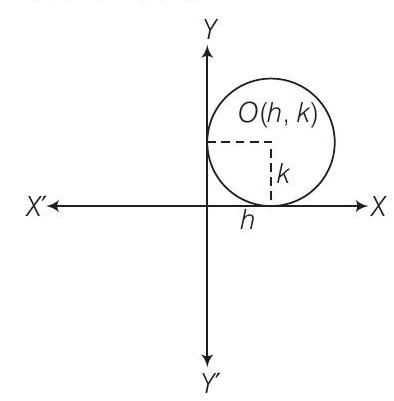
So, the equation of required circle is
2. Show that the point
Show Answer
Solution
Given points are
3. If a circle passes through the points
Thinking Process
General equation of the circle passing through the origin is
Now, satisfied the given points to get the values of
Show Answer
Solution
Let the equation of circle is
Since, this circle passes through the points
From Eq. (ii),
From Eq. (iii),
Hence, the coordinates of the circle are
4. Find the equation of the circle which touches
Show Answer
Solution
Given that, centre of the circle is
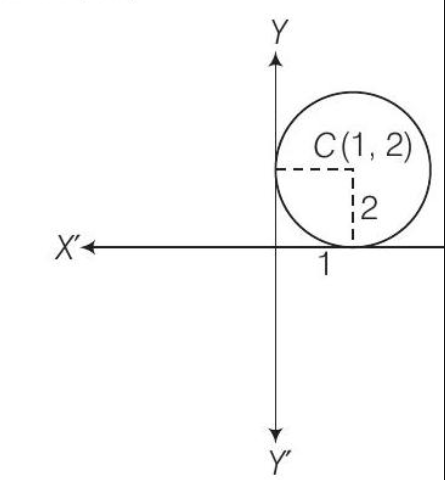
So, the equation of circle is
5. If the lines
Thinking Process
The distance between two parallel lines
i.e.,
Show Answer
Solution
Given lines,
or
It is clear that lines (i) and (ii) parallel.
Now, distance between them i.e.,
and radius of the circle
6. Find the equation of a circle which touches both the axes and the line
Show Answer
Solution
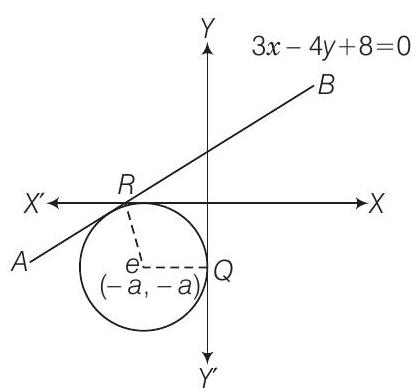
Let
| But | |
|---|---|
So, the equation of circle is
7. If one end of a diameter of the circle
Thinking Process
First of all get the centre of the circle from the given equation, then find the mid-point of the diameter of the circle.
Show Answer
Solution
Given equation of the circle is
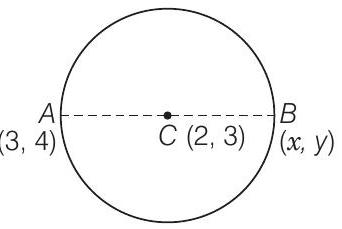
So, the centre of the circle is
Since, the mid-point of
Then,
and
So, the coordinates of other end of the diameter will be
8. Find the equation of the circle having
Show Answer
Solution
Given that, centre of the circle is
and
From Eq. (i)
Now,
Since, point
Now, equation of the circle is
9. If the line
Show Answer
Solution
Given equation of circle,
Now, perpendicular from
Since the distance from the point
10. Find the equation of a circle concentric with the circle
Show Answer
Solution
Given equation of the circle is
[since, the circles are concentric]
Let radius of the required circle
So, the required equation of circle is
11. If the latusrectum of an ellipse is equal to half of minor axis, then find its eccentricity.
Show Answer
Solution
Consider the equation of the ellipse is
Length of minor axis
and length of latusrectum
Given that,
We know that,
12. If the ellipse with equation
Thinking Process
Find the values of
Show Answer
Solution
Given equation of ellipse,
Foci
13. If the eccentricity of an ellipse is
Show Answer
Solution
Given that, eccentricity
Let equation of the ellipse be
Since the foci of this ellipse is
We know that,
14. Find the equation of ellipse whose eccentricity is
Thinking Process
First of all find the values of
Show Answer
Solution
Given that,
So, the required equation of the ellipse is
15. Find the distance between the directrices of ellipse
Show Answer
Solution
The equation of ellipse is
On comparing this equation with
We know that,
Now,
and
16. Find the coordinates of a point on the parabola
Thinking Process
The distance of a point
Show Answer
Solution
Given parabola is
On comparing this parabola to the
So, the points are
17. Find the length of the line segment joining the vertex of the parabola
Show Answer
Solution
Given equation of the parabola is
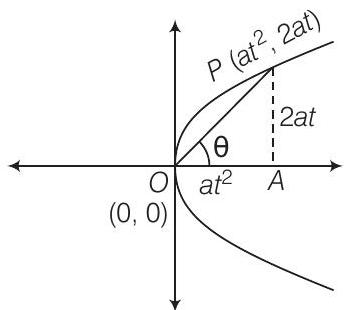
Let the coordinates of any point
18. If the points
Show Answer
Solution
Given that the coordinates, vertex of the parabola
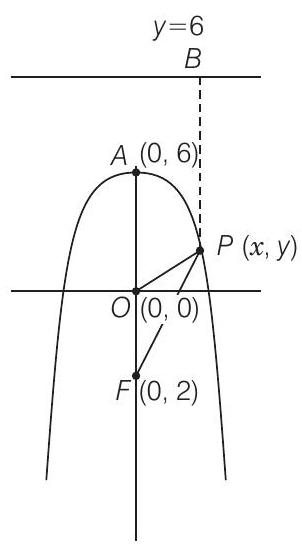
By definition of the parabola,
19. If the line
Show Answer
Solution
Given that, line
and
From Eqs. (i) and (ii),
20. If the distance between the foci of a hyperbola is 16 and its eccentricity is
Thinking Process
First of all find the value of
Show Answer
Solution
Distance between the foci i.e., and
We know that,
So, the equation of hyperbola is
21. Find the eccentricity of the hyperbola
Show Answer
Solution
Given equation of the hyperbola is
Since, this equation in form of
22. Find the equation of the hyperbola with eccentricity
Show Answer
Solution
Given that eccentricity i.e.,
So, the equation of hyperbola is
Long Answer Type Questions
23. If the lines
Thinking Process
First of all find the intersection point of the given lines, then get radius of circle from given area. Now, use formula equation of circle with centre
Show Answer
Solution
Given lines are
and
Since the intersection point of these lines will be coordinates of the circle i.e., coordinates of the circle as
Let the radius of the circle is
Then
So, the equation of circle is
24. Find the equation of the circle which passes through the points
Show Answer
Solution
Let the general equation of the circle is
Since, this circle passes through the points
Since, the centre of the circle
i.e.,
From Eq. (iv),
On putting
From Eqs. (ii) and (iii),
From Eqs. (ii) and (vi),
25. Find the equation of a circle whose centre is
Show Answer
Solution
Given centre of the circle is
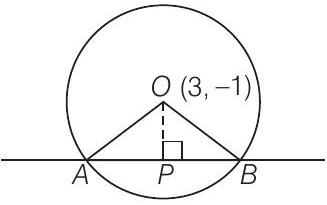
Now,
So, the radius of circle is
26. Find the equation of a circle of radius 5 which is touching another circle
Show Answer
Solution
Let the coordinates of centre of the required circle are
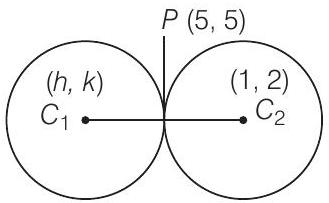 Radius
Radius Conic Sections
So, it is clear that
So, the equation of and required circle is
27. Find the equation of a circle passing through the point
Thinking Process
First of all let the equation of a circle with centre
Show Answer
Solution
Let equation of circle be
Now, the circle passes through the point
On putting
When
When
So, the equation of circle when centre
When centre
28. Find the equation of each of the following parabolas
(i) directrix
(ii) vertex at
(iii) focus at
Show Answer
Solution
(i) Given that, directrix
So, the equation of the parabola
(ii) Given that, vertex
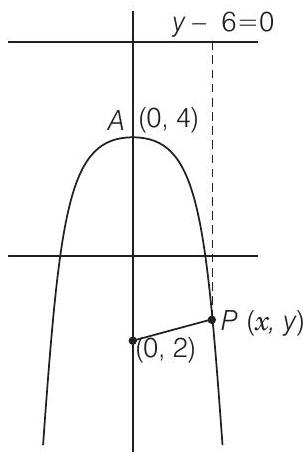
So, the equation of parabola is
(iii) Given that, focus at
So, the equation of parabola is
29. Find the equation of the set of all points the sum of whose distances from the points
Show Answer
Solution
Let the coordinates of the point be
Conic Sections
On squaring both sides, we get
30. Find the equation of the set of all points whose distance from
Thinking Process
Consider the points
Show Answer
Solution
Let the point be
So, the distance from the line
31. Show that the set of all points such that the difference of their distances from
Show Answer
Solution
Let the points be
and the distance of
Now,
On squaring both sides, we get
32. Find the equation of the hyperbola with
(i) Vertices
(ii) Vertices
(iii) Foci
Show Answer
Solution
(i) Given that, vertices
So,the equation of parabola is
(ii) Vertices
So, the equation of hyperbola is
(iii) Given that, foci
Since, this hyperbola passes through the point
So, the equation of hyperbola is
True/False
33. The line
Thinking Process
If a line is the diameter of circle, then the centre of the circle should lies on line. Use this property to solve the given problem.
Show Answer
Solution
False
Given equation of the circle is
So, this line is not diameter of the circle.
34. The shortest distance from the point
Show Answer
Solution
False
Given circle is
and
So, the distance between the point
35. If the line
Show Answer
Solution
True
Given circle is
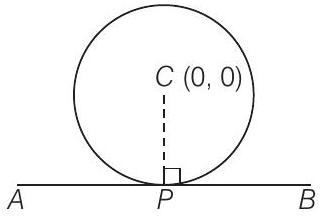
So,
36. The point
Thinking Process
If the
Show Answer
Solution
False
Given circle is
Since, the point is
Now,
So, the
37. The line
Show Answer
Solution
True
Given equation of a line is
and
From Eq. (i),
38. If
Show Answer
Solution
False
Given equation of the ellipse is
which is in form of
Let the coordinate of point
39. The line
Show Answer
Solution
True
Given equation of line is
and
Since, the equation of tangent at
Hence, the statement is true.
40. The locus of the point of intersection of lines
Thinking Process
First of all eliminate
Show Answer
Solution
True
Given equations of line are
and
From Eq. (i),
Fillers
41. The equation of the circle having centre at
Show Answer
Solution
The perpendicular distance from centre
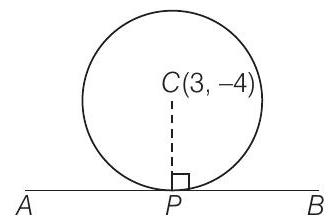
So, the required equations of the circle is
42. The equation of the circle circumscribing the triangle whose sides are the lines
Show Answer
Solution
Given equations of line are
From Eqs. (i) and (ii),
On putting
From Eqs. (i) and (iii),
When
From Eqs. (ii) and (iii)
Now,
Let the equation of circle is
Since, the points
From Eqs. (iv), (v) and (vi),
So, the equation of circle is
43. An ellipse is described by using an endless string which is passed over two pins. If the axes are
Show Answer
Solution
Let equation of the ellipse be
We know that,
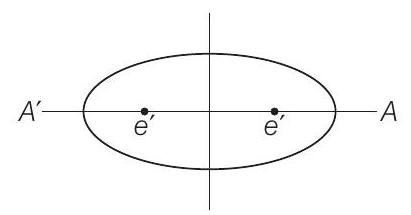
44. The equation of the ellipse having foci
Thinking Process
First of all get the value of
Show Answer
Solution
Given that, foci of the ellipse are
So, the equation of ellipse is
45. The equation of the parabola having focus at
Show Answer
Solution
Given that, focus at
Let any point on the parabola be
46. The equation of the hyperbola with vertices at
Show Answer
Solution
Let the equation of the hyperbola be
Then vertices
So, the equation of hyperbola is,
Objective Type Questions
47. The area of the circle centred at
(a)
(b)
(c)
(d) None of these
Show Answer
Solution
(c) Given that, centre of the circle is
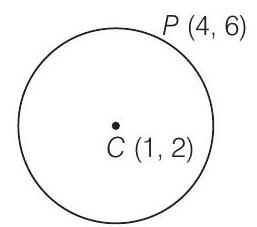
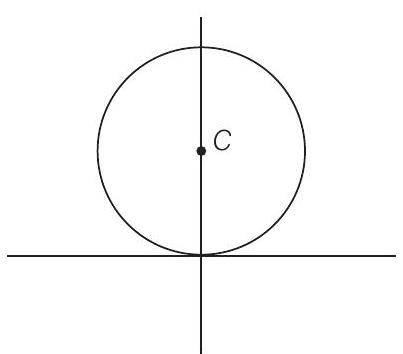
48. Equation of a circle which passes through
(a)
(b)
(c)
(d) None of these
Show Answer
Solution
(c) Let centre of the circle be
Since, the point
So, the equation of circle is
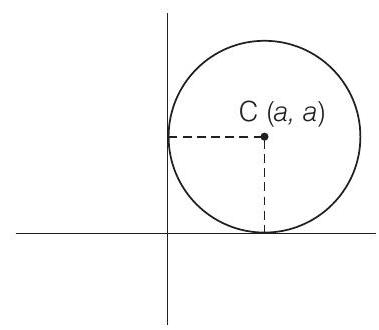
49. Equation of the circle with centre on the
(a)
(b)
(c)
(d)
Show Answer
Solution
(c) Let general equation of the circle is
Since the point
So, the equation of circle is
50. The equation of a circle with origin as centre and passing through the vertices of an equilateral triangle whose median is of length
(a)
(b)
(c)
(d)
Show Answer
Solution
(c) Given that, length of the median
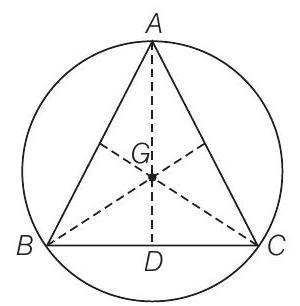
So, the equation of the circle is
51. If the focus of a parabola is
(a)
(b)
(c)
(d)
Show Answer
Solution
(a) Given that, focus of parabola at
Let any point on the parabola is
Then,
52. If the parabola
(a)
(b)
(c)
(d) 4
Show Answer
Solution
(b) Given that, parabola is
Since, the parabola passes through the point
Then,
53. If the vertex of the parabola is the point
(a)
(b)
(c)
(d)
Show Answer
Solution
(a) Here, vertex
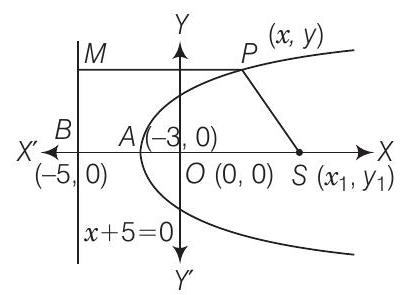
Since, axis of the parabola is a line perpendicular to directrix and
54. If equation of the ellipse whose focus is
(a)
(b)
(c)
(d) None of the above
Show Answer
Solution
(a) Given that, focus of the ellipse is
Let
55. The length of the latusrectum of the ellipse
(a) 4
(b) 3
(c) 8
(d)
Thinking Process
First of all find the value of
Show Answer
Solution
(d) Given equation of ellipse is
56. If
(a)
(b)
(c)
(d)
Show Answer
Solution
(b) Given that,
We know that,
57. The eccentricity of the hyperbola whose latusrectum is 8 and conjugate axis is equal to half of the distance between the foci is
(a)
(b)
(c)
(d) None of these
Show Answer
Solution
(c) Length of latusrectum of the hyperbola i.e.,
Since, transverse axis be
From Eqs. (i) and (ii),
58. The distance between the foci of a hyperbola is 16 and its eccentricity is
(a)
(b)
(c)
(d) None of these
Thinking Process
The distance between the foci of hyperbola is
Show Answer
Solution
(a) Given that, distance between the foci of hyperbola
59. Equation of the hyperbola with eccentricity
(a)
(b)
(c)
(d) None of these
Show Answer
Solution
(a) Given that, eccentricity of the hyperbola,
and
So, the equation of the hyperbola is






