Linear Inequalities
Short Answer Type Questions
Solve for
1.
Thinking Process
First solve the first two inequalities, then solve the last two inequality to get range of
Show Answer
Solution
Consider first two inequalities,
and consider last two inequalities,
[subtracting 3 to both sides]
[dividing by 3 ]
…(ii)
From Eqs. (i) and (ii),
2.
Thinking Process
First, let
Show Answer
Solution
Let
3.
Show Answer
Solution
Given,
On combining results of Eqs. (i) and (ii), we get
4.
Show Answer
Solution
On combining Eqs. (i) and (ii), we get
5.
Show Answer
Solution
We have,
[multiplying by 4 on both sides]
6.
Show Answer
Solution
We have,
On combining Eqs. (i) and (ii), we see that solution is not possible because nothing is common between these two solutions. (i.e.,
7. A company manufactures cassettes. Its cost and revenue functions are
Show Answer
Solution
Cost function, C(x) = 26000 + 30x
and revenue function, R(x) = 43x
For profit, R(x) > C(x)
8. The water acidity in a pool is considered normal when the average pH reading of three daily measurements is between 8.2 and 8.5 . If the first two
Show Answer
Solution
Given,
and
first
second
Let third
Since, it is given that average
Thus, third pH value lies between 7.77 and 8.67 .
9. A solution of
Show Answer
Solution
Let
Then, total quantity of mixture
Total acid content in the
It is given that acid content in the resulting mixture must be more than
Therefore,
Taking last two inequalities,
Hence, the number of litres of the
10. A solution is to be kept between
Show Answer
Solution
Let the required temperature be
Given that,
Since, temperature in degree calcius lies between
Hence, the range of temperature in degree fahrenheit is
11. The longest side of a triangle is twice the shortest side and the third side is
Show Answer
Solution
Let the length of shortest side be
According to the given information,
Longest side
and third side
Perimeter of triangle
According to the question,
Perimeter
Hence, the minimum length of shortest side be
12. In drilling world’s deepest hole it was found that the temperature
Show Answer
Solution
Given that,
According to the question,
Hence, at the depth 8 to
Long Answer Type Questions
13. Solve the following system of inequalities
Show Answer
Solution
The given system of inequations is
Since, the intersection of Eqs. (iii) and (iv) is the null set. Hence, the given system of equation has no solution.
14. Find the linear inequalities for which the shaded region in the given figure is the solution set.
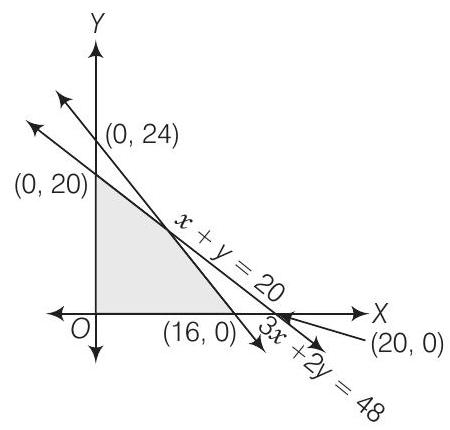
Show Answer
Solution
Consider the line
Now, consider the line
We also notice that the shaded region is above
Thus, the linear inequations corresponding to the given solution set are
15. Find the linear inequalities for which the shaded region in the given figure is the solution set.
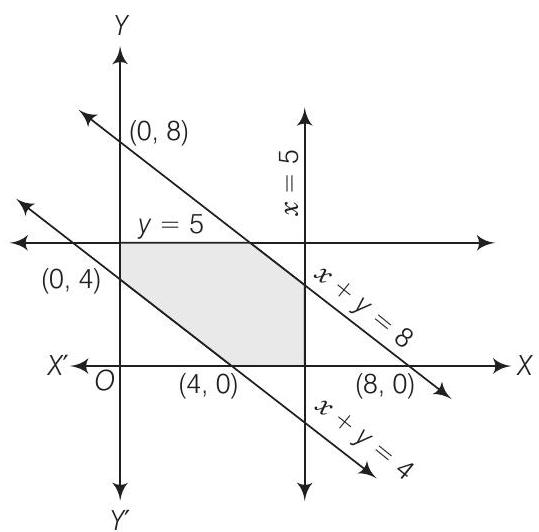
Show Answer
Solution
Consider the line
We observe that the shaded region and the origin lie on the opposite side of this line and
Consider the line
Consider the line
Hence,
Consider the line
Therefore,
We also notice that the shaded region is above the
Thus, the linear inequations comprising the given solution set are
16. Show that the following system of linear inequalities has no solution
Show Answer
Solution
Consider the inequation
| 3 | 1 | 0 | |
| 0 | 1 | 1.5 |
Now,
So, half plane contains
Consider the inequation
| 0 | 4 | 2 | |
|---|---|---|---|
| 3 | 0 |
Thus, coordinate axis intersected by the line
Now,
Therefore, half plane of the solution does not contained
Consider the inequation
It represents a straight line parallel to
Now,
Therefore, half plane of the solution does not contains
Clearly
The solution set of the given linear constraints will be the intersection of the above region.
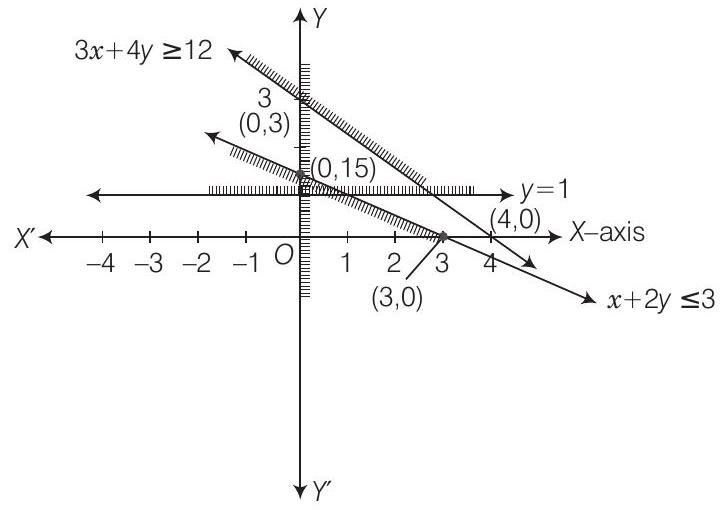
It is clear from the graph the shaded portions do not have common region.
So, solution set is null set.
17. Solve the following system of linear inequalities
Show Answer
Solution
Consider the inequation
| 0 | 8 | 4 | |
|---|---|---|---|
| 12 | 0 | 6 |
Hence, line
Now,
Therefore, half plane of the solution set does not contains
Consider the inequation
| 0 | 5 | 3 | |
| 15 | 0 | 6 |
Line
Now, point
Therefore, the half plane of the solution contain origin.
Consider the inequality
It represents a straight line parallel to
Therefore, half plane does not contains
The graph of the above inequations is given below.
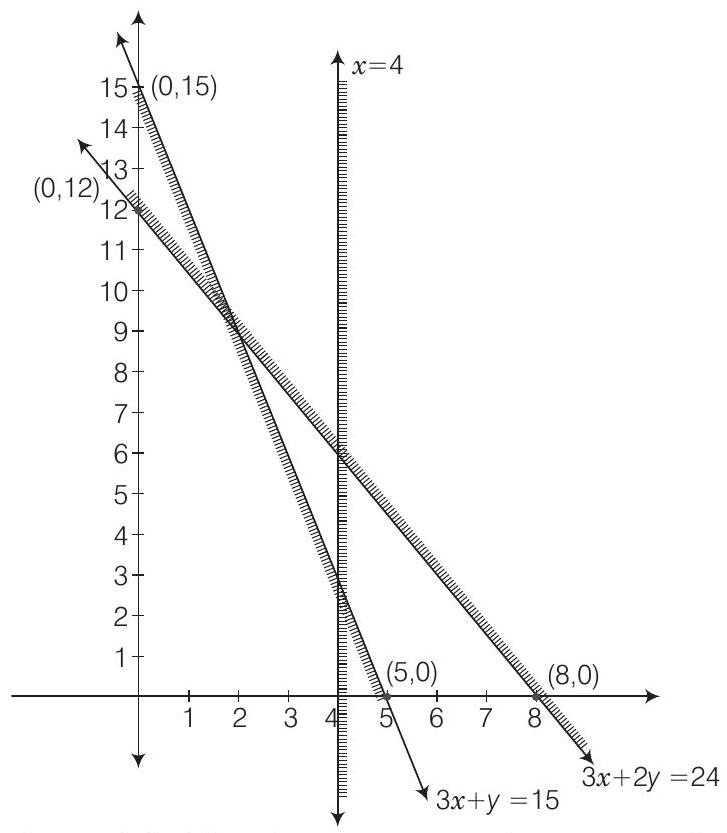
It is clear from the graph that there is no common region corresponding to these inequality. Hence, the given system of inequalities have no solution.
18. Show that the solution set of the following system of linear inequalities is an unbounded region
Show Answer
Solution
Consider the inequation
2x + y = 8
y = 8-2x
| 0 | 0 | 4 | 3 | |||||
|---|---|---|---|---|---|---|---|---|
| 8 | 0 | 2 |
The line
Consider the inequation
| 10 | 0 | 8 | |
|---|---|---|---|
| 0 | 5 | 1 |
The line
Now, point
Therefore, half plane does not contain
Consider the inequation
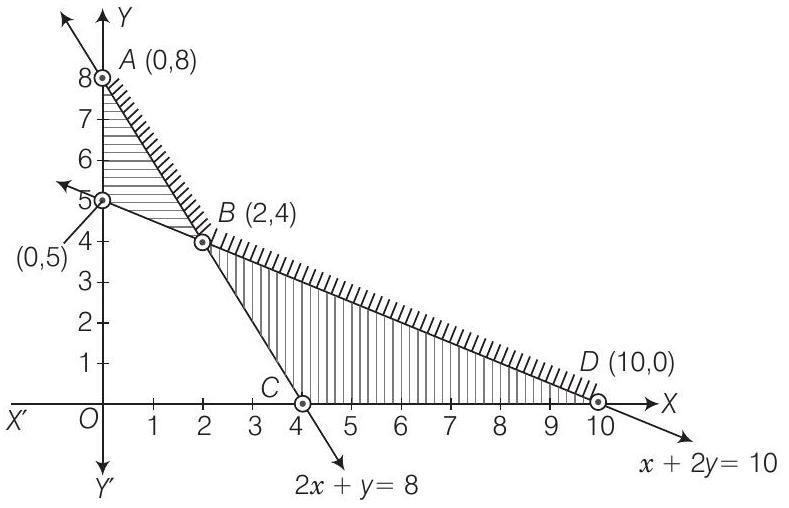
It is clear from the graph that common shaded portion is unbounded.
Objective Type Questions
19. If
(a)
(b)
(c)
(d)
Show Answer
Solution
(c) If
[if we multiply by negative numbers, then inequality get reversed]
20. If
(a)
(b)
(c)
(d)
Show Answer
Solution
(c) It is given that,
21. If
(a)
(b)
(c)
(d)
Show Answer
Solution
(a) Given that,
| [multiplying by -1 on both sides] | ||
|---|---|---|
| [adding 17 on both sides] | ||
22. If
(a)
(b)
(c)
(d)
Show Answer
Solution
(b) Given,
23. Let
(a)
(b)
(c)
(d)
Show Answer
Solution
(d) Given,
24. If
(a)
(b)
(c)
(d)
Show Answer
Solution
(c) Given,
25. If
(a)
(b)
(c)
(d)
Show Answer
Solution
(b) Given,
The inequality representing the following graphs is
26.
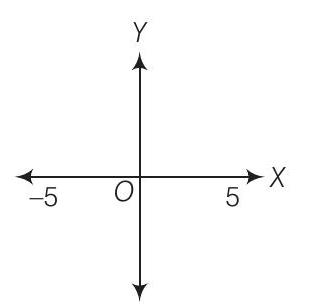
(a)
(b)
(c)
(d)
Show Answer
Solution
(a) The given graph represent
On combining these two result, we get
Solution of a linear inequality in variable
27.
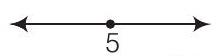
(a)
(b)
(d)
Show Answer
Solution
(d) The given graph represents all the values greater than 5 except
28.
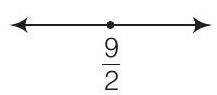
(a)
(b)
(c)
(d)
Show Answer
Solution
(b) The given graph represents all the values greater than
29
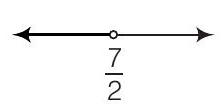
(a)
(b)
(c)
(d)
Show Answer
Solution
(a) The given graph represents all the values less than
30.
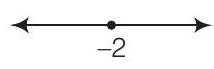
(a)
(b)
(c)
(d)
Show Answer
Solution
(b) The given graph represents all values less than -2 including -2 .
True/False
31. State which of the following statements is true of false.
(i) If
(ii) If
(iii) If
(iv) If
(v) If
(vi) If
(vii) If
(viii) If
(ix) If
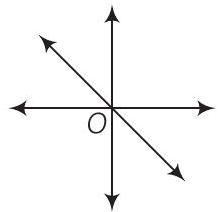
(x) Graph of
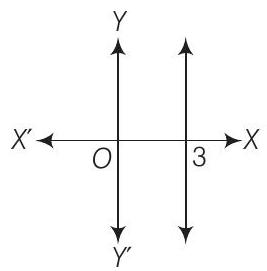
(xi) Graph of
(xii) Graph of
(xiii) Solution set of
(xiv) Solution set of
(xv) Solution set of
Show Answer
Solution
(i) If
Hence, statement (i) is false.
(ii) If
Hence, statement (ii) is true.
(iii) If
Hence, statement (iii) is true.
(iv) If
(v) If
Hence, statement (v) is true.
(vi) If
Hence, statement (vi) is false.
(vii) If
Hence, statement (vii) is true.
(viii) If
Hence, statement (viii) is false.
(ix) If
Hence, statement (ix) is true.
(x) The given graph represents
Hence, statement
(xi) The given graph represents
Hence, statement (xi) is true.
(xii) The given graph represent
Hence, statement (xii) is false.
(xiii) Solution set of
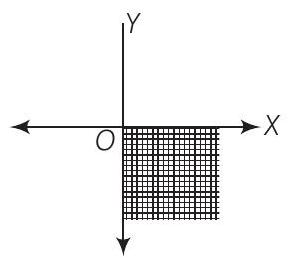
Hence, statement (xiii) is false.
(xiv) Solution set of
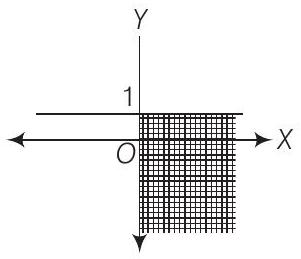
Hence, statement (xiv) is false.
(xv) The given graph represents
Hence, statement (xv) is correct.
Fillers
32. Fill in the blanks of the following
(i) If
(ii) If
(iii) If
(iv) If
(v) If
(vi) If
(vii) If
(viii) If
Show Answer
Solution
(i) If
(ii) If
(iii) If
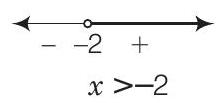
(iv) If
(v) If
(vi) If
then
e.g., consider
(vii) If
(viii) If






