SATHEE: Trigonometric Functions

Trigonometric Functions

Short Answer Type Questions

1. Prove that $\frac{\tan A + \sec A - 1}{\tan A - \sec A + 1} = \frac{1 + \sin A}{\cos A}$ .

Thinking Process

Here, use the formulae i.e., $\sec^{2} A - \tan^{2} A = 1$ and $a^{2} - b^{2} = (a + b) (a - b)$ to solve the above problem.

Show Answer

Solution

$\begin{aligned} L H S & = \frac{\tan A + \sec A - 1}{\tan A - \sec A + 1} \\ = \frac{\tan A + \sec A - (\sec^{2} A - \tan^{2} A)}{(\tan A - \sec A + 1)} \\ [∵ \sec^{2} A - \tan^{2} A = 1] \\ = \frac{(\tan A + \sec A) - (\sec A + \tan A) (\sec A - \tan A)}{(1 - \sec A + \tan A)} \\ = \frac{(\sec A + \tan A) (1 - \sec A + \tan A)}{1 - \sec A + \tan A} \\ = \sec A + \tan A = \frac{1}{\cos A} + \frac{\sin A}{\cos A} \\ = \frac{1 + \sin A}{\cos A} = R H S Hence proved. \end{aligned}$

2. If $\frac{2 \sin α}{1 + \cos α + \sin α} = y$ , then prove that $\frac{1 - \cos α + \sin α}{1 + \sin α}$ is also equal to $y$ .

Show Answer

Solution

Given that, $\frac{2 \sin α}{1 + \cos α + \sin α} = y$

$\begin{aligned} Now, & \frac{1 - \cos α + \sin α}{1 + \sin α} \\ = \frac{(1 - \cos α + \sin α)}{(1 + \sin α)} \cdot \frac{(1 + \cos α + \sin α)}{(1 + \cos α + \sin α)} \\ = \frac{(1 + \sin α) - \cos α}{(1 + \sin α)} \cdot \frac{(1 + \sin α) + \cos α}{(1 + \cos α + \sin α)} \\ = \frac{(1 + \sin α)^{2} - \cos^{2} α}{(1 + \sin α) (1 + \sin α + \cos α)} \\ = \frac{(1 + \sin^{2} α + 2 \sin α) - \cos^{2} α}{(1 + \sin α) (1 + \sin α + \cos α)} \end{aligned}$

$\begin{aligned} = \frac{1 + \sin^{2} α + 2 \sin α - 1 + \sin^{2} α}{(1 + \sin α) (1 + \sin α + \cos α)} \\ = \frac{2 \sin^{2} α + 2 \sin α}{(1 + \sin α) (1 + \sin α + \cos α)} \\ = \frac{2 \sin α (1 + \sin α)}{(1 + \sin α) (1 + \sin α + \cos α)} \\ = \frac{2 \sin α}{1 + \sin α + \cos α} = y \end{aligned}$

Hence proved.

3. If $m \sin θ = n \sin (θ + 2 α)$ , then prove that $\tan (θ + α) \cot α = \frac{m + n}{m - n}$ .

Show Answer

Solution

Given that,

$\begin{aligned} Given that, \begin{aligned} m \sin θ & = n \sin (θ + 2 α) \\ ∴ & \frac{\sin (θ + 2 α)}{\sin θ} = \frac{m}{n} \end{aligned} \end{aligned}$

Using componendo and dividendo, we get

$\begin{array}{r} \frac{\sin (θ + 2 α) + \sin θ}{\sin (θ + 2 α) - \sin θ} = \frac{m + n}{m - n} \\ \Rightarrow \frac{2 \sin \frac{θ + 2 α + θ}{2} \cdot \cos \frac{θ + 2 α - θ}{2}}{2 \cos \frac{θ + 2 α + θ}{2} \cdot \sin \frac{θ + 2 α - θ}{2}} = \frac{m + n}{m - n} \\ \Rightarrow [∵ \sin x + \sin y = 2 \sin \frac{x + y}{2} \cdot \cos \frac{x - y}{2} . \\ and . \sin x - \sin y = 2 \cos \frac{x + y}{2} \sin \cdot \frac{x - y}{2}] \\ \Rightarrow \frac{\sin (θ + α) \cdot \cos α}{\cos (θ + α) \cdot \sin α} = \frac{m + n}{m - n} \\ \tan (θ + α) \cdot \cot α = \frac{m + n}{m - n} Hence proved. \end{array}$

4. If $\cos (α + β) = \frac{4}{5}$ and $\sin (α - β) = \frac{5}{13}$ , where $α$ lie between 0 and $\frac{π}{4}$ , then find that value of $\tan 2 α$ .

Show Answer

Solution

Given that,

$\cos (α + β) = \frac{4}{5} and \sin (α - β) = \frac{5}{13}$

$\Rightarrow \sin (α + β) = \sqrt{1 - \frac{16}{25}} = \sqrt{\frac{9}{25}} = \pm \frac{3}{5}$

$∴ \sin (α + β) = \frac{3}{5}$

$and \cos (α - β) = \sqrt{1 - \frac{25}{169}} = \sqrt{\frac{144}{169}} = \pm \frac{12}{13}$

$∴ \cos (α - β) = \frac{12}{13}$

$Now, \tan (α + β) = \frac{\sin (α + β)}{\cos (α + β)}$

$[since, α lies between 0 and \frac{π}{4}]$

$= \frac{\frac{3}{5}}{\frac{4}{5}} = \frac{3}{4}$

$and \tan (α - β) = \frac{\sin (α - β)}{\cos (α - β)} = \frac{\frac{5}{13}}{\frac{12}{13}} = \frac{5}{12}$

$∴ \tan 2 α = \tan (α + β + α - β)$

$= \frac{\tan (α + β) + \tan (α - β)}{1 - \tan (α + β) \cdot \tan (α - β)} [∵ \tan (x \pm y) = \frac{\tan x \pm \tan y}{1 \mp \tan x \cdot \tan y}]$

$= \frac{\frac{3}{4} + \frac{5}{12}}{1 - \frac{3}{4} \cdot \frac{5}{12}} = \frac{\frac{9 + 5}{12}}{\frac{16 - 5}{16}} = \frac{14 \times 16}{12 \times 11} = \frac{56}{33}$

5. If $\tan x = \frac{b}{a}$ , then find the value of $\sqrt{\frac{a + b}{a - b}} + \sqrt{\frac{a - b}{a + b}}$ .

Thinking Process

First of all rationalise the given expression and used the formula, i.e., $\cos 2 x = \cos^{2} x - \sin^{2} x$ .

Show Answer

Solution

Given that, $\tan x = \frac{b}{a}$

$∴ \sqrt{\frac{a + b}{a - b}} + \sqrt{\frac{a - b}{a + b}} = \frac{\sqrt{(a + b)^{2}} + \sqrt{(a - b)^{2}}}{\sqrt{(a - b) (a + b)}}$

$= \frac{(a + b) + (a - b)}{\sqrt{a^{2} - b^{2}}} = \frac{2 a}{\sqrt{a^{2} - b^{2}}} = \frac{2 a}{a \sqrt{1 - \frac{b}{a}}} [∵ \frac{b}{a} = \tan]$

$= \frac{2}{\sqrt{1 - \tan^{2} x}} = \frac{2 \cos x}{\sqrt{\cos^{2} x - \sin^{2} x}} [∵ \cos 2 x = \cos^{2} x - \sin^{2} x] x$

$= \frac{2 \cos x}{\sqrt{\cos 2 x}}$

6. Prove that $\cos θ \cos \frac{θ}{2} - \cos 3 θ \cos \frac{9 θ}{2} = \sin 7 θ \sin 8 θ$ .

Show Answer

Solution

LHS $= \cos θ \cos \frac{θ}{2} - \cos 3 θ \cos \frac{9 θ}{2}$

$\begin{aligned} = \frac{1}{2} 2 \cos θ \cdot \cos \frac{θ}{2} - 2 \cos 3 θ \cdot \cos \frac{9 θ}{2} \\ = \frac{1}{2} \cos θ + \frac{θ}{2} + \cos θ - \frac{θ}{2} - \cos 3 θ + \frac{9 θ}{2} - \cos 3 θ - \frac{9 θ}{2} \\ = \frac{1}{2} (\cos \frac{3 θ}{2} + \cos \frac{θ}{2} - \cos \frac{15 θ}{2} - \cos \frac{3 θ}{2} . \\ = \frac{1}{2} \cos \frac{θ}{2} - \cos \frac{15 θ}{2} \end{aligned}$

$= - \frac{1}{2} 2 \sin \frac{θ + 15 θ}{2} \cdot \sin \frac{θ - 15 θ}{2}$

$[∵ \cos x - \cos y = - 2 \sin \frac{x + y}{2} \cdot \sin \frac{x - y}{2}]$

$= + (\sin 8 θ \cdot \sin 7 θ) = R H S$

$∴ LHS = RHS$

Hence Proved

7. If $a \cos θ + b \sin θ = m$ and $a \sin θ - b \cos θ = n$ , then show that $a^{2} + b^{2} = m^{2} + n^{2}$ .

Show Answer

Solution

Given that,

and

$a \cos θ + b \sin θ = m . . (i)$

$a \sin θ - b \cos θ = n . . (i i)$

On squaring and adding of Eqs. (i) and (ii), we get

$m^{2} + n^{2} = (a \cos θ + b \sin θ)^{2} + (a \sin θ - b \cos θ)^{2}$

$= a^{2} \cos^{2} θ + b^{2} \sin^{2} θ + 2 a b \sin θ \cdot \cos θ + a^{2} \sin^{2} θ + b^{2} \cos^{2} θ$

$\Rightarrow m^{2} + n^{2} = a^{2} (\cos^{2} θ + \sin^{2} θ) + b^{2} (\sin^{2} θ + \cos^{2} θ) - 2 a b \sin θ \cdot \cos θ$

$\Rightarrow m^{2} + n^{2} = a^{2} + b^{2} Hence proved.$

8. Find the value of $\tan 22^{\circ} 30^{'}$ .

Show Answer

Solution

Let

$Let θ = 45^{\circ}$

$We know that, \tan \frac{θ}{2} = \frac{\sin \frac{θ}{2}}{\cos \frac{θ}{2}} = \frac{2 \sin \frac{θ}{2} \cdot \cos \frac{θ}{2}}{2 \cos^{2} \frac{θ}{2}} \Rightarrow \tan \frac{θ}{2} = \frac{\sin θ}{1 + \cos θ}$

$∴ \tan 22^{\circ} 30^{'} = \frac{\sin 45^{\circ}}{1 + \cos 45^{\circ}} [∵ θ = 45^{\circ}]$

$= \frac{\frac{1}{\sqrt{2}}}{1 + \frac{1}{\sqrt{2}}} = \frac{1}{\sqrt{2} + 1}$

9. Prove that $\sin 4 A = 4 \sin A \cos^{3} A - 4 \cos A \sin^{3} A$ .

Thinking Process

Here, apply the formula i.e., $\sin 2 x = 2 \sin x \cos x$ and $\cos 2 x = \cos^{2} x - \sin^{2} x$

Show Answer

Solution

$L H S = \sin 4 A$

$= 2 \sin 2 A \cdot \cos 2 A$

$= 2 (2 \sin A \cdot \cos A) (\cos^{2} A - \sin^{2} A)$

$= 4 \sin A \cdot \cos^{3} A - 4 \cos A \sin^{3} A$

$[∵ \cos 2 A = \cos^{2} A - \sin^{2} A and \sin 2 A = 2 \sin A \cdot \cos A]$

$∴ L H S = R H S Hence Proved$

10. If $\tan θ + \sin θ = m$ and $\tan θ - \sin θ = n$ , then prove that $m^{2} - n^{2} = 4 \sin θ \tan θ$ .

Show Answer

Solution

Now,

Also, Given that,

$\tan θ + \sin θ = m . . (i)$

$and \tan θ - \sin θ = n . . (i i)$

$Now m + n = \tan θ + \sin θ + \tan θ - \sin θ$

$m + n = 2 \tan θ \dots (i i i)$

$also m - n = \tan θ + \sin θ - \tan θ + \sin θ$

$m - n = 2 \sin θ \dots (i v)$

From Eqs. (iii) and (iv),

$\begin{aligned} (m + n) (m - n) & = 4 \sin θ \cdot \tan θ \\ m^{2} - n^{2} & = 4 \sin θ \cdot \tan θ Hence Proved \end{aligned}$

11. If $\tan (A + B) = p$ and $\tan (A - B) = q$ , then show that $\tan 2 A = \frac{p + q}{1 - p q}$ .

Show Answer

Solution

Given that $\tan (A + B) = p . . (i)$

and $\tan (A - B) = q . . (i i)$

$∴ \tan 2 A = \tan (A + B + A - B)$

$= \frac{\tan (A + B) + \tan (A - B)}{1 - \tan (A + B) \tan (A - B)} [∵ \tan (x + y) = \frac{\tan x + \tan y}{1 - \tan x \tan y}]$

$= \frac{p + q}{1 - p q}$ [from Eqs. (i) and (ii)]

12. If $\cos α + \cos β = 0 = \sin α + \sin β$ , then prove that $\cos 2 α + \cos 2 β = - 2 \cos (α + β)$ .

Show Answer

Solution

Given that, $\cos α + \cos β = 0 = \sin α + \sin β$

$\Rightarrow (\cos α + \cos β)^{2} - (\sin α + \sin β)^{2} = 0$

$\Rightarrow \cos^{2} α + \cos^{2} β + 2 \cos α \cos β - \sin^{2} α - \sin^{2} β - 2 \sin α \sin β = 0$

$\Rightarrow \cos^{2} α - \sin^{2} α + \cos^{2} β - \sin^{2} β = 2 (\sin α \sin β - \cos α \cos β)$

$\Rightarrow \cos 2 α + \cos 2 β = - 2 \cos (α + β)$

Hence proved.

13. If $\frac{\sin (x + y)}{\sin (x - y)} = \frac{a + b}{a - b}$ , then show that $\frac{\tan x}{\tan y} = \frac{a}{b}$ .

Show Answer

Solution

Given that, $\frac{\sin (x + y)}{\sin (x - y)} = \frac{a + b}{a - b}$

Using componendo and dividendo,

$\Rightarrow= \frac{\sin (x + y) + [\sin (x - y)]}{\sin (x + y) - \sin (x - y)} = \frac{a + b + a - b}{a + b - a + b}$

$\Rightarrow= \frac{2 \sin \frac{x + y + x - y}{2} \cdot \cos \frac{x + y - x + y}{2}}{2 \cos \frac{x + y + x - y}{2} \cdot \sin \frac{x + y - x + y}{2}} = \frac{2 a}{2 b}$

$[∵ \sin x + \sin y = 2 \sin \frac{x + y}{2} \cdot \cos \frac{x - y}{2} and \sin x - \sin y = 2 \cos \frac{x + y}{2} \cdot \sin \frac{x - y}{2}]$

$\Rightarrow= \frac{\sin x \cdot \cos y}{\cos x \cdot \sin y} = \frac{a}{b}$

$\frac{\tan x}{\tan y} = \frac{a}{b}$

14. If $\tan θ = \frac{\sin α - \cos α}{\sin α + \cos α}$ , then show that $\sin α + \cos α = \sqrt{2} \cos θ$ .

Show Answer

Solution

Given that, $\tan θ = \frac{\sin α - \cos α}{\sin α + \cos α}$

$\begin{matrix} \Rightarrow \tan θ = \frac{\cos α (\tan α - 1)}{\cos α (\tan α + 1)} \\ \Rightarrow \tan θ = \frac{\tan α - \tan \frac{π}{4}}{1 + \tan \frac{π}{4} \cdot \tan α} & [∵ \tan \frac{π}{4} = 1] \end{matrix}$

Trigonometric Functions

$\Rightarrow \tan θ = \tan (α - \frac{π}{4})$

$\Rightarrow θ = α - \frac{π}{4} \Rightarrow α = θ + \frac{π}{4}$

$∴ \sin α + \cos α = \sin (θ + \frac{π}{4}) + \cos (θ + \frac{π}{4})$

$= \sin θ \cdot \cos \frac{π}{4} + \cos θ \cdot \sin \frac{π}{4} + \cos θ \cdot \cos \frac{π}{4} - \sin θ \cdot \sin \frac{π}{4}$

$= \frac{1}{\sqrt{2}} \sin θ + \frac{1}{\sqrt{2}} \cos θ + \frac{1}{\sqrt{2}} \cos θ - \frac{1}{\sqrt{2}} \sin θ [∵ \sin \frac{π}{4} = \cos \frac{π}{4} = \frac{1}{\sqrt{2}}]$

$= \frac{2}{\sqrt{2}} \cdot \cos θ = \sqrt{2} \cos θ$

15. If $\sin θ + \cos θ = 1$ , then find the general value of $θ$ .

Thinking Process

If $\sin θ = \sin α$ , then $θ = n π + (- 1)^{n} \cdot α$ , gives general solution of the given equation.

Show Answer

Solution

Given that, $\sin θ + \cos θ = 1$

On squaring both sides, we get

$\sin^{2} θ + \cos^{2} θ + 2 \sin θ \cdot \cos θ = 1$

$\Rightarrow 1 + 2 \sin θ \cdot \cos = 1 [∵ \sin 2 x = 2 \sin x \cos x]$

$\Rightarrow \sin 2 θ = 02 θ = n π + (- 1)^{n} \cdot 0$

$∴ θ = \frac{n π}{2}$

Alternate Method

$\sin θ + \cos θ = 1$

$\Rightarrow \frac{1}{\sqrt{2}} \cdot \sin θ + \frac{1}{\sqrt{2}} \cdot \cos θ = \frac{1}{\sqrt{2}}$

$\Rightarrow \sin θ \cdot \cos \frac{π}{4} + \cos θ \cdot \sin \frac{π}{4} = \frac{1}{\sqrt{2}} ∵ \sin \frac{π}{4} = \frac{1}{\sqrt{2}} = \cos \frac{π}{4}$

$\Rightarrow \sin θ + \frac{π}{4} = \sin \frac{π}{4} [∵ \sin (x + y) = \sin x \cdot \cos y + \cos x \cdot \sin y]$

$\Rightarrow θ + \frac{π}{4} = n π + (- 1)^{n} \frac{π}{4}$

$∴ θ = n π + (- 1)^{n} \frac{4}{4} - \frac{π}{4}$

16. Find the most general value of $θ$ satisfying the equation $\tan θ = - 1$ and $\cos θ = \frac{1}{\sqrt{2}}$ .

Show Answer

Solution

The given equations are

$\tan θ = - 1 . . (i)$

$and \cos θ = \frac{1}{\sqrt{2}} . . (i i)$

$From Eq. (i), \tan θ = - \tan \frac{π}{4}$

$\Rightarrow \tan θ = \tan (2 π - \frac{π}{4}) \Rightarrow \tan θ = \tan \frac{7 π}{4}$

$∴ θ = \frac{7 π}{4}$

From Eq. (ii),

$\Rightarrow \cos θ = \cos (2 π - \frac{π}{4}) \Rightarrow \cos θ = \cos \frac{7 π}{4}$

$∴ θ = \frac{7 π}{4}$

Hence, the most general value of $θ$ i.e., $θ = 2 n π + \frac{7 π}{4}$ .

17. If $\cot θ + \tan θ = 2 c o s e c θ$ , then find the general value of $θ$ .

Show Answer

Solution

Given that,

$\cot θ + \tan θ = 2 c o s e c θ$

$\frac{\cos θ}{\sin θ} + \frac{\sin θ}{\cos θ} = \frac{2}{\sin θ}$

$\Rightarrow \frac{\cos^{2} + \sin^{2} θ}{\sin θ \cdot \cos θ} = \frac{2}{\sin θ}$

$\Rightarrow \frac{1}{\cos θ} = 2 [∵ \sin^{2} θ + \cos^{2} θ = 1]$

$\Rightarrow \cos θ = \frac{1}{2} \Rightarrow \cos θ = \cos \frac{π}{3}$

$∴ θ = 2 n π \pm \frac{π}{3}$

18. If $2 \sin^{2} θ = 3 \cos θ$ , where $0 \leq θ \leq 2 π$ , then find the value of $θ$ .

Show Answer

Solution

Given that,

$Given that , 2 \sin^{2} θ = 3 \cos θ$

$\Rightarrow 2 - 2 \cos^{2} θ = 3 \cos θ$

$\Rightarrow 2 \cos^{2} θ + 3 \cos θ - = 0$

$\Rightarrow 2 \cos^{2} θ + 4 \cos θ - \cos θ - 2 = 0$

$\Rightarrow 2 \cos θ (\cos θ + 2) - 1 (\cos θ + 2) = 0$

$\Rightarrow (\cos θ + 2) (2 \cos θ - 1) = 0$

$\Rightarrow \cos θ = - 2 n o t p o s s i b l e [∵ - 1 \leq \cos θ \leq 1]$

$\Rightarrow 2 \cos θ = 1$

$\Rightarrow \cos θ = \frac{1}{2}$

$\Rightarrow \cos θ = \cos \frac{π}{3}$

$∴ θ = \frac{π}{3}$

$A l s o, \cos θ = \cos (2 π - \frac{π}{3})$

$\Rightarrow \cos θ = \cos \frac{5 π}{6}$

$∴ θ = \frac{5 π}{6}$

So, the values of $θ$ are $\frac{π}{3}$ and $\frac{5 π}{6}$ .

19. If $\sec x \cos 5 x + 1 = 0$ , where $0 < x \leq \frac{π}{2}$ , then find the value of $x$ .

Show Answer

Solution

Given that, $\sec x \cos 5 x + 1 = 0$

$\frac{\cos 5 x}{\cos x} + 1 = 0 \Rightarrow \cos 5 x + \cos x = 0$

$\Rightarrow 2 \cos (\frac{5 x + x}{2}) \cdot \cos (\frac{5 x - x}{2}) = 0$

$[∵ \cos x + \cos y = 2 \cos \frac{x + y}{2} \cdot \cos \frac{x - y}{2}]$

$\Rightarrow 2 \cos 3 x \cdot \cos 2 x = 0$

$\Rightarrow \cos 3 x = 0 or \cos 2 x = 0$

$\Rightarrow \cos 3 x = \cos \frac{π}{2} or \cos 2 x = \cos \frac{π}{2}$

$∴ 3 x = \frac{π}{2} \Rightarrow 2 x = \frac{π}{2}$

$x = \frac{π}{6} \Rightarrow x = \frac{π}{4}$

Hence, the solutions are $\frac{π}{2}, \frac{π}{4}$ and $\frac{π}{6}$ .

Long Answer Type Questions

20. If $\sin (θ + α) = a$ and $\sin (θ + β) = b$ , then prove that $\cos (α + β) - 4 a b \cos (α - β) = 1 - 2 a^{2} - 2 b^{2}$ .

$∵$ Thinking Process

Express $\cos (α - β) = \cos (θ + α) - (θ + β)$

Show Answer

Solution

Given that, $\sin (θ + α) = a . . (i)$

and

$\sin (θ + β) = b . . (i i)$

$∴ \cos (θ + α) = \sqrt{1 - a^{2}}$ and $\cos (θ + β) = \sqrt{1 - b^{2}}$

$∴ \cos (α - β) = \cos θ + α - (θ + β)$

$= \cos (θ + β) \cos (θ + α) + \sin (θ + α) \sin (θ + β)$

$\begin{aligned} = \sqrt{1 - a^{2}} \sqrt{1 - b^{2}} + a \cdot b = a b + \sqrt{(1 - a^{2}) (1 - b^{2})} \\ = a b + \sqrt{1 - a^{2} - b^{2} + a^{2} b^{2}} \end{aligned}$

and

$\cos (α - β) = a b + \sqrt{1 - a^{2} - b^{2} + a^{2} b^{2}}$

$= \cos 2 (α - β) - 4 a b \cos (α - β)$

$= 2 \cos^{2} (α - β) - 1 - 4 a b \cos (α - β)$

$= 2 \cos (α - β) (\cos α - β - 2 a b) - 1$

$= 2 (a b + \sqrt{1 - a^{2} - b^{2} + a^{2} b^{2}}) (a b + \sqrt{1 - a^{2} - b^{2} + a^{2} b^{2}} - 2 a b) - 1$

$= 2 [(\sqrt{1 - a^{2} - b^{2} + a^{2} b^{2} + a b}) (\sqrt{1 - a^{2} - b^{2} + a^{2} b^{2}} - a b)] - 1$

$= 2 [1 - a^{2} - b^{2} + a^{2} b^{2} - a^{2} b^{2}] - 1$

$= 2 - 2 a^{2} - 2 b^{2} - 1$

$= 1 - 2 a^{2} - 2 b^{2} H e n c e P r o v e d$

21. If $\cos (θ + φ) = m \cos (θ - φ)$ , then prove that $\tan θ = \frac{1 - m}{1 + m} \cot φ$ .

Show Answer

Solution

Given that,

$\begin{aligned} \cos (θ + φ) = m \cos (θ - φ) \\ \Rightarrow \frac{\cos (θ + φ)}{\cos (θ - φ)} = \frac{m}{1} \end{aligned}$

Using componendo and dividendo rule,

$\frac{\cos (θ - φ) - \cos (θ + φ)}{\cos (θ - φ) + \cos (θ + φ)} = \frac{1 - m}{1 + m}$

$\Rightarrow \frac{- 2 \sin \frac{θ - φ + θ + φ}{2} \cdot \sin \frac{θ - φ - θ - φ}{2}}{2 \cos \frac{θ - φ + θ + φ}{2} \cdot \cos \frac{θ - φ - θ - φ}{2}} = \frac{1 - m}{1 + m}$

$\Rightarrow \frac{\sin θ \cdot \sin φ}{\cos θ \cdot \cos φ} = \frac{1 - m}{1 + m} [∵ \sin (- θ) = - \sin θ a n d \cos (- θ) = \cos θ]$

$\Rightarrow \tan θ \cdot \tan φ = \frac{1 - m}{1 + m}$

$\Rightarrow \tan θ = \frac{1 - m}{1 + m} \cot φ$

22. Find the value of the expression

$3 [\sin^{4} \frac{3 π}{2} - α + \sin^{4} (3 π + α)] - 2 [\sin^{6} (\frac{π}{2} + α) + \sin^{6} (5 π - α)] .$

Show Answer

Solution

Given expression,

$\begin{aligned} 3 [\sin^{4} & (\frac{3 π}{2}) - α + \sin^{4} (3 π + α)] - 2 [\sin^{6} \frac{π}{2} + α + \sin^{6} (5 π - α)] \\ = 3 [\cos^{4} α + \sin^{4} (π + α)] - 2 [\cos^{6} α + \sin^{6} (π - α)] \\ = 3 [\cos^{4} α + \sin^{4} α] - 2 [\cos^{6} α + \sin^{6} α] = 3 - 2 = 1 \end{aligned}$

23. If $a \cos 2 θ + b \sin 2 θ = c$ has $α$ and $β$ as its roots, then prove that $\tan α + \tan β = \frac{2 b}{a + c}$ .

Show Answer

Solution

Given that, $a \cos 2 θ + b \sin 2 θ = c$

$\Rightarrow a \frac{1 - \tan^{2} θ}{1 + \tan^{2} θ} + b \frac{2 \tan θ}{1 + \tan^{2} θ} = c$

$[∵ \sin 2 θ = \frac{2 \tan θ}{1 + \tan^{2} θ} and \cos 2 θ = \frac{1 - \tan^{2} θ}{1 + \tan^{2} θ}]$

$\Rightarrow a (1 - \tan^{2} θ) + 2 b \tan θ = c (1 + \tan^{2} θ)$

$\Rightarrow a - a - \tan^{2} θ + 2 b \tan θ = c + c \tan^{2} θ$

$\Rightarrow (a + c) \tan^{2} θ - 2 b \tan θ + c - a = 0$

Since, this equation has $\tan α$ and $\tan β$ as its roots.

$∵ \tan α + \tan β = \frac{- (- 2 b)}{a + c} = \frac{2 b}{a + c}$

24. If $x = \sec φ - \tan φ$ and $y = c o s e c φ + \cot φ$ , then show that $x y + x - y + 1 = 0$ .

Show Answer

Solution

Given that, and $x = \sec φ - \tan φ . . (i)$

Now,

$y = c o s e c φ + \cot φ . . (i i)$

$\Rightarrow x y = \sec φ \cdot c o s e c φ - c o s e c φ \cdot \tan φ + \sec φ \cdot \cot φ - \tan φ \cdot \cot φ$

$\Rightarrow x y = \sec φ \cdot c o s e c φ - \frac{1}{\cos φ} + \frac{1}{\sin φ} - 1$

$\Rightarrow 1 + x y = \sec φ c o s e c φ - \sec φ + c o s e c φ . . (i i i)$

From Eqs. (i) and (ii), we get

$x - y = \sec φ - \tan φ - c o s e c φ - \cot φ$

$\Rightarrow x - y = \sec φ - c o s e c φ - \frac{\sin φ}{\cos φ} - \frac{\cos φ}{\sin φ}$

$\Rightarrow x - y = \sec φ - c o s e c φ - (\frac{\sin^{2} φ + \cos^{2} φ}{\sin φ \cdot \cos φ})$

$\Rightarrow x - y = \sec φ - c o s e c φ - \frac{1}{\sin φ \cdot \cos φ}$

$\begin{aligned} \Rightarrow x - y = \sec φ - c o s e c φ - c o s e c φ \cdot \sec φ \\ \Rightarrow x - y = - (\sec φ \cdot c o s e c φ - \sec φ + c o s e c φ) \\ \Rightarrow x - y = - (x y + 1) \\ \Rightarrow x y + x - y + 1 = 0 [from Eq. (iii)] Hence proved. \end{aligned}$

25. If $θ$ lies in the first quadrant and $\cos θ = \frac{8}{17}$ , then find the value of $\cos (30^{\circ} + θ) + \cos (45^{\circ} - θ) + \cos (120^{\circ} - θ)$ .

Show Answer

Solution

Given that,

$\Rightarrow \sin θ = \sqrt{\frac{289 - 64}{289}}$

$\Rightarrow \sin θ = \pm \frac{15}{17}$

$\Rightarrow \sin θ = \frac{15}{17} [Since, θ lies in first quadrant]$

$Now, \cos (30^{\circ} + θ) + \cos (45^{\circ} - θ) + \cos (120^{\circ} - θ)$

$= \cos (30^{\circ} + θ) + \cos (45^{\circ} - θ) + \cos (90^{\circ} + 30^{\circ} - θ)$

$= \cos (30^{\circ} + θ) + \cos (45^{\circ} - θ) - \sin (30^{\circ} - θ)$

$= \cos 30^{\circ} \cos θ - \sin 30^{\circ} \sin θ + \cos 45^{\circ} \cos θ + \sin 45^{\circ} \sin θ$

$= \frac{\sqrt{3}}{2} \cos θ - \frac{1}{2} \sin θ + \frac{1}{\sqrt{2}} \cos θ + \frac{1}{\sqrt{2}} \sin θ - \frac{1}{2} \cos θ \frac{\sqrt{3}}{2} \sin θ$

$= \frac{\sqrt{3}}{2} + \frac{1}{\sqrt{2}} - \frac{1}{2} \cos θ + \frac{1}{\sqrt{2}} - \frac{1}{2} + \frac{\sqrt{3}}{2} \sin θ$

$= \frac{\sqrt{6} + 2 - \sqrt{2}}{2 \sqrt{2}} \cos θ + \frac{2 - \sqrt{2} + \sqrt{6}}{2 \sqrt{2}} \sin θ$

$= \frac{\sqrt{6} + 2 - \sqrt{2}}{2 \sqrt{2}} \frac{8}{17} + \frac{2 - \sqrt{2} + \sqrt{6}}{2 \sqrt{2}} \frac{15}{17}$

$\begin{aligned} = \frac{1}{17 (2 \sqrt{2})} (8 \sqrt{6} + 16 - 8 \sqrt{2} + 30 - 15 \sqrt{2} + 15 \sqrt{6}) \\ = \frac{1}{17 (2 \sqrt{2})} (23 \sqrt{6} - 23 \sqrt{2} + 46) \\ = \frac{23 \sqrt{6}}{17 (2 \sqrt{2})} - \frac{23 \sqrt{2}}{17 (2 \sqrt{2})} + \frac{46}{17 (2 \sqrt{2})} \\ = \frac{23 \sqrt{3}}{17 (2)} - \frac{23}{17 (2)} + \frac{23}{17 \sqrt{2}} \\ = \frac{23}{17} \frac{\sqrt{3} - 1}{2} + \frac{1}{\sqrt{2}} \end{aligned}$

26. Find the value of $\cos^{4} \frac{π}{8} + \cos^{4} \frac{3 π}{8} + \cos^{4} \frac{5 π}{8} + \cos^{4} \frac{7 π}{8}$ .

Show Answer

Solution

Given expression, $\cos^{4} \frac{π}{8} + \cos^{4} \frac{3 π}{8} + \cos^{4} \frac{5 π}{8} + \cos^{4} \frac{7 π}{8}$

$\begin{aligned} = \cos^{4} \frac{π}{8} + \cos^{4} \frac{3 π}{8} + \cos^{4} π - \frac{3 π}{8} + \cos^{4} π - \frac{π}{8} \\ = \cos^{4} \frac{π}{8} + \cos^{4} \frac{3 π}{8} + \cos^{4} (\frac{3 π}{8}) + \cos^{4} (\frac{π}{8}) \\ = 2 [\cos^{4} \frac{π}{8} + \cos^{4} \frac{3 π}{8}] = 2 [\cos^{4} \frac{π}{8} + \cos^{4} (\frac{π}{2} - \frac{π}{8})] \\ = 2 [\cos^{4} \frac{π}{8} + \sin^{4} \frac{π}{8}] \\ = 2 [\cos^{2} \frac{π}{8} + \sin^{2} \frac{π^{2}}{8} - 2 \cos^{2} \frac{π}{8} \cdot \sin^{2} \frac{π}{8}] \\ = 21 - 2 \cos^{2} \frac{π}{8} \cdot \sin^{2} \frac{π}{8} = 2 - 2 \sin \frac{π}{8} \cdot \cos \frac{π^{2}}{8} \\ = 2 - \sin (\frac{2 π}{8})^{2} = 2 - (\frac{1}{\sqrt{2}}) \\ = 2 - \frac{1}{2} = \frac{3}{2} \end{aligned}$

27. Find the general solution of the equation $5 \cos^{2} θ + 7 \sin^{2} θ - 6 = 0$ .

Show Answer

Solution

Given equation,

$\begin{matrix} \Rightarrow 5 \cos^{2} θ + 7 \sin^{2} θ - 6 & = 0 \\ \Rightarrow 5 \cos^{2} + 7 (1 - \cos^{2} θ) - 6 & = 0 \\ \Rightarrow 5 \cos^{2} θ + 7 - 7 \cos^{2} θ - 6 & = 0 \\ \Rightarrow 5 \cos^{2} θ + 7 - 7 \cos^{2} θ - 6 & = 0 \Rightarrow & \Rightarrow - 2 \cos^{2} θ + 1 = 0 \\ \Rightarrow 2 \cos^{2} θ - 1 = 0 & [∵ \cos^{2} θ = \cos^{2} α] \\ \Rightarrow \cos^{2} θ = \frac{1}{2} & ∴ θ = n π \pm α \\ \Rightarrow \cos^{2} θ & = \cos^{2} \frac{π}{4} \\ θ & = n π \pm \frac{π}{4} \end{matrix}$

28. Find the general of the equation $\sin x - 3 \sin 2 x + \sin 3 x$ $= \cos x - 3 \cos 2 x + \cos 3 x$ .

Show Answer

Solution

Given equation, $\sin x - 3 \sin 2 x + \sin 3 x = \cos x - 3 \cos 2 x + \cos 3 x$

$\begin{aligned} \Rightarrow 2 \sin (\frac{x + 3 x}{2}) \cdot \cos (\frac{3 x - x}{2}) - 3 \sin 2 x \\ = 2 \cos (\frac{3 x + x}{2}) \cdot \cos (\frac{3 x - x}{2}) - 3 \cos 2 x \\ \Rightarrow 2 \sin 2 x \cos x - 3 \sin 2 x = 2 \cos 2 x \cdot \cos x - 3 \cos 2 x \\ \Rightarrow \sin 2 x (2 \cos x - 3) = \cos 2 x (2 \cos x - 3) \\ \Rightarrow \frac{\sin 2 x}{\cos 2 x} = 1 \\ \begin{array}{c} \Rightarrow & \tan 2 x = 1 \end{array} \\ \Rightarrow \tan 2 x = \tan \frac{π}{4} \\ \Rightarrow 2 x = n π + \frac{π}{4} \\ ∴ x = \frac{n π}{2} + \frac{4}{8} \end{aligned}$

29. Find the general solution of the equation

Show Answer

Solution

Given equation is,

$(\sqrt{3} - 1) \cos θ + (\sqrt{3} + 1) \sin θ = 2 . . (i)$

$\begin{aligned} Put \sqrt{3} - 1 = r \sin α and \sqrt{3} + 1 = r \cos α \\ ∴ r^{2} = (\sqrt{3} - 1)^{2} + (\sqrt{3} + 1)^{2} \\ \Rightarrow = 3 + 1 - 2 \sqrt{3} + 3 + 1 + 2 \sqrt{3} \\ \Rightarrow r^{2} = 8 \\ ∴ r = 2 \sqrt{2} \\ now, \tan α = \frac{\sqrt{3} - 1}{\sqrt{3} + 1} = \frac{\tan \frac{π}{3} - \tan \frac{π}{4}}{1 + \tan \frac{π}{3} \cdot \frac{π}{4}} \\ \Rightarrow \tan α = \tan \frac{π}{3} - \frac{π}{4} \\ \Rightarrow \tan α = \tan \frac{π}{12} \\ ∴ α = \frac{π}{12} \end{aligned}$

From Eq. (i), $r \sin α \cos θ + r \cos α \sin θ = 2$

$\begin{matrix} \Rightarrow & r [\sin (θ + α)] = 2 \\ \sin (θ + α) = \frac{2}{2 \sqrt{2}} \\ \Rightarrow & \sin (θ + α) = \frac{1}{\sqrt{2}} \\ \Rightarrow & \sin (θ + α) = \sin \frac{π}{4} θ + α = n π + (- 1)^{n} \frac{π}{4} \\ θ = n π + (- 1)^{n} \cdot \frac{π}{4} - \frac{π}{12} \end{matrix}$

Alternate Method

$\begin{aligned} (\sqrt{3} - 1) \cos θ + (\sqrt{3} + 1) \sin θ & = 2 \\ Put \sqrt{3} - 1 & = r \cos α and \sqrt{3} + 1 = r \sin α \\ ∴ r & = 2 \sqrt{2} \end{aligned}$

Now, $\tan α = \frac{\sqrt{3} + 1}{\sqrt{3} - 1} = \frac{1 + \frac{1}{\sqrt{3}}}{1 - \frac{1}{\sqrt{3}}}$

$\begin{aligned} \Rightarrow \tan α = \frac{\tan \frac{π}{4} + \tan \frac{π}{6}}{1 - \tan \frac{π}{4} \cdot \tan \frac{π}{6}} \\ \Rightarrow \tan α = \tan \frac{π}{4} + \frac{π}{6} \Rightarrow \tan α = \tan \frac{5 π}{12} \end{aligned}$

$α = \frac{5 π}{12}$

From Eq. (i), $r \cos α \cos θ + r \sin α \sin θ = 2$

$r [\cos (θ - α)]$

$\Rightarrow \cos (θ - α) = \frac{2}{2 \sqrt{2}}$

$\Rightarrow \cos (θ - α) = \frac{1}{\sqrt{2}}$

$\Rightarrow \cos (θ - α) = \cos \frac{π}{4}$

$\Rightarrow θ - α = 2 n π \pm \frac{π}{4}$

$∴ θ = 2 n π \pm \frac{π}{4} + \frac{5 π}{12}$

Objective Type Questions

30. If $\sin θ + c o s e c θ = 2$ , then $\sin^{2} θ + c o s e c^{2} θ$ is equal to

(a) 1

(b) 4

(d) None of these

Show Answer

Solution

$\Rightarrow \sin^{2} θ + c o s e c^{2} θ + 2 \sin θ \cdot c o s e c θ = 4$

$\Rightarrow \sin^{2} θ + c o s e c^{2} θ = 4 - 2$

$\Rightarrow \sin^{2} θ + c o s e c^{2} θ = 2$

31. If $f (x) = \cos^{2} x + \sec^{2} x$ , then

(a) $f (x) < 1$

(b) $f (x) = 1$

(d) $f (x) \geq 2$

Show Answer

Solution

(d) Given that, $f (x) = \cos^{2} x + \sec^{2} x$

We know that, $A M \geq G M$

$\frac{\cos^{2} x + \sec^{2} x}{2} \geq \sqrt{\cos^{2} x \cdot \sec^{2} x}$

$\Rightarrow$

$\cos^{2} x + \sec^{2} x \geq 2$

$[∵ \cos x \cdot \sec x = 1]$

$\Rightarrow f (x) \geq 2$

32. If $\tan θ = \frac{1}{2}$ and $\tan φ = \frac{1}{3}$ , then the value of $θ + φ$ is

(a) $\frac{π}{6}$

(b) $π$

(d) $\frac{π}{4}$

Show Answer

Solution

(d) Given that,

$\begin{matrix} Now, & \tan (θ + φ) = \frac{\tan θ + \tan φ}{1 - \tan θ \cdot \tan φ} \\ \Rightarrow & \tan (θ + φ) = \frac{\frac{1}{2} + \frac{1}{3}}{1 - \frac{1}{2} \cdot \frac{1}{3}} \Rightarrow \tan (θ + φ) = \frac{\frac{3 + 2}{\frac{6}{6}}}{\frac{6 - 1}{6}} = \frac{5}{5} = 1 \\ \Rightarrow & \tan (θ + φ) = \tan \frac{π}{4} \\ ∴ & θ + φ = \frac{π}{4} \end{matrix}$

33. Which of the following is not correct?

(a) $\sin θ = - \frac{1}{5}$

(b) $\cos θ = 1$

(d) $\tan θ = 20$

Show Answer

Solution

Hence, $\sec θ$ cannot be equal to $\frac{1}{2}$ .

34. The value of $\tan 1^{\circ} \tan 2^{\circ} \tan 3^{\circ} \dots \tan 89^{\circ}$ is

(a) 0

(b) 1

(d) Not defined

Show Answer

Solution

(b) Given expression, $\tan 1^{\circ} \tan 2^{\circ} \tan 3^{\circ} \dots \tan 89^{\circ}$

$\begin{aligned} = \tan 1^{\circ} \tan 2^{\circ} \dots \tan 45^{\circ} \cdot \tan (90^{\circ} - 44^{\circ}) \tan (90^{\circ} - 43^{\circ}) \dots \tan (90^{\circ} - 1^{\circ}) \\ = \tan 1^{\circ} \cdot \cot 1^{\circ} \cdot \tan 2^{\circ} \cdot \cot 2^{\circ} \dots \tan 89^{\circ} \cdot \cot 89^{\circ} \\ = 1 \cdot 1 \dots 1 \cdot 1 = 1 \end{aligned}$

35. The value of $\frac{1 - \tan^{2} 15^{\circ}}{1 + \tan^{2} 15^{\circ}}$ is

(a) 1

(b) $\sqrt{3}$

(d) 2

Show Answer

Solution

$\begin{aligned} Let θ = 15^{\circ} \\ We know that, \cos 2 θ = \overset{―}{1 + \tan^{2} θ} \\ ∴ \cos 30^{\circ} = \frac{1 - \tan^{2} 15^{\circ}}{1 + \tan^{2} 15^{\circ}} \\ \Rightarrow \frac{1 - \tan^{2} 15^{\circ}}{1 + \tan^{2} 15^{\circ}} = \frac{\sqrt{3}}{2} [∵ \cos 30^{\circ} = \frac{\sqrt{3}}{2}] \end{aligned}$

36. The value of $\cos 1^{\circ} \cos 2^{\circ} \cos 3^{\circ} \dots \cos 179^{\circ}$ is

(a) $\frac{1}{\sqrt{2}}$

(b) 0

(d) -1

Show Answer

Solution

(b) Given expression, $\cos 1^{\circ} \cos 2^{\circ} \cos 3^{\circ} \dots \cos 179^{\circ}$

$\begin{aligned} = \cos 1^{\circ} \cos 2^{\circ} \dots \cos 90^{\circ} \dots \cos 179^{\circ} [∵ \cos 90^{\circ} = 0] \\ = 0 \end{aligned}$

37. If $\tan θ = 3$ and $θ$ lies in third quadrant, then the value of $\sin θ$ is

(a) $\frac{1}{\sqrt{10}}$

(b) $- \frac{1}{\sqrt{10}}$

(d) $\frac{3}{\sqrt{10}}$

Show Answer

Solution

(c)

$Given that, \tan θ = 3$

$\Rightarrow \sec^{2} θ = 1 + \tan^{2} θ$

$\Rightarrow \sec θ = \sqrt{1 + 9} = \pm \sqrt{10}$

$\Rightarrow \sec θ = - \sqrt{10}$

$\Rightarrow \cos θ = - \frac{1}{\sqrt{10}}$

$\Rightarrow \sin θ = \pm \sqrt{1 - \frac{1}{10}} = \pm \sqrt{\frac{9}{10}} = \pm \frac{3}{\sqrt{10}}$ [since, $θ$ lies in third quadrant]

$∴ \sin θ = - \frac{3}{\sqrt{10}}$

38. The value of $\tan 75^{\circ} - \cot 75^{\circ}$ is

(a) $2 \sqrt{3}$

(b) $2 + \sqrt{3}$

(d) 1

Show Answer

Solution

(a) Given expression, $\tan 75^{\circ} - \cot 75^{\circ}$

$\begin{aligned} = \frac{\sin 75^{\circ}}{\cos 75^{\circ}} - \frac{\cos 75^{\circ}}{\sin 75^{\circ}} \\ = \frac{\sin^{2} 75^{\circ} - \cos^{2} 75^{\circ}}{\sin 75^{\circ} \cdot \cos_{7}^{\circ}} \\ = \frac{- 2 \cos 150^{\circ}}{\sin 150^{\circ}} \\ = \frac{- 2 \cos (90^{\circ} + 60^{\circ})}{\sin (90^{\circ} + 60^{\circ})} \\ = \frac{+ 2 \sin 60^{\circ}}{\cos 60^{\circ}} \\ = \frac{2 \cdot \frac{\sqrt{3}}{2}}{\frac{1}{2}} = 2 \sqrt{3} \end{aligned}$

39. Which of the following is correct?

(a) $\sin 1^{\circ} > \sin 1$

(b) $\sin 1^{\circ} < \sin 1$

(d) $\sin 1^{\circ} = \frac{π}{18^{\circ}} \sin 1$

Show Answer

Solution

(b) We know that, if $θ$ is increasing, then $\sin θ$ is also increasing.

$∴ \sin 1^{\circ} < \sin 1 [∵ 1 r a d = 57^{\circ 30}]$

40. If $\tan α = \frac{m}{m + 1}$ and $\tan β = \frac{1}{2 m + 1}$ , then $α + β$ is equal to

(a) $\frac{π}{2}$

(b) $\frac{π}{3}$

(d) $\frac{π}{4}$

Show Answer

Solution

(d) Given that, $\tan α = \frac{m}{m + 1}$ and $\tan β = \frac{1}{2 m + 1}$

Now, $\tan (α + β) = \frac{\tan α + \tan β}{1 - \tan α \cdot \tan β}$

$\begin{matrix} \Rightarrow & \tan (α + β) = \frac{\frac{m}{m + 1} + \frac{1}{2 m + 1}}{1 - \frac{m}{m + 1} \frac{1}{2 m + 1}} \\ \Rightarrow & \tan (α + β) = \frac{m (2 m + 1) + m + 1}{(m + 1) (2 m + 1) - m} \\ \Rightarrow & \tan (α + β) = \frac{2 m^{2} + m + m + 1}{2 m^{2} + 2 m + m + 1 - m} \\ \Rightarrow & \tan (α + β) = \frac{2 m^{2} + 2 m + 1}{2 m^{2} + 2 m + 1} \Rightarrow \tan (α + β) = 1 \\ ∴ & α + β = \frac{π}{4} \end{matrix}$

41. The minimum value of $3 \cos x + 4 \sin x + 8$ is

(a) 5

(b) 9

(d) 3

Thinking Process

For the expression $A \cos θ + B \sin θ$ , then the minimum value is $- \sqrt{A^{2} + B^{2}}$ .

Show Answer

Solution

(d) Given expression, $3 \cos x + 4 \sin x + 8$

$\begin{matrix} Let & y = 3 \cos x + 4 \sin x + 8 \\ \Rightarrow & y - 8 = 3 \cos x + 4 \sin x \\ ∴ & Minimum value of y - 8 = - \sqrt{9 + 16} \\ \Rightarrow & y - 8 = - 5 \Rightarrow y = - 5 + 8 \\ ∴ & y = 3 \end{matrix}$

Hence, the minimum value of $3 \cos x + 4 \sin x + 8$ is 3 .

42. The value of $\tan 3 A - \tan 2 A - \tan A$ is

(a) $\tan 3 A \tan 2 A \tan A$

(b) $- \tan 3 A \tan 2 A \tan A$

(d) None of the above

Show Answer

Solution

(a)

$\begin{aligned} Let 3 A & = A + 2 A \\ \tan 3 A & = \tan (A + 2 A) \end{aligned}$

$\Rightarrow \tan 3 A = \frac{\tan A + \tan 2 A}{1 - \tan A \cdot \tan 2 A}$

$\Rightarrow \tan A + \tan 2 A = \tan 3 A - \tan 3 A \cdot \tan 2 A \cdot \tan A$

$\Rightarrow \tan 3 A - \tan 2 A - \tan A = \tan 3 A \cdot \tan 2 A \cdot \tan A$

43. The value of $\sin (45^{\circ} + θ) - \cos (45^{\circ} - θ)$ is

(a) $2 \cos θ$

(b) $2 \sin θ$

(d) 0

Thinking Process

Use formula i.e., $\sin (A + B) = \sin A \cos B + \cos A \sin B$ and $\cos (A - B) = \cos A \cos B + \sin A \sin B$ .

Show Answer

Solution

(d) Given expression,

$\begin{aligned} \sin (45^{\circ} + θ) & - \cos (45^{\circ} - θ) \\ = \sin 45^{\circ} \cdot \cos θ + \cos 45^{\circ} \cdot \sin θ - \cos 45^{\circ} \cdot \cos θ - \sin 45^{\circ} \cdot \sin θ \\ = \frac{1}{\sqrt{2}} \cdot \cos θ + \frac{1}{\sqrt{2}} \cdot \sin θ - \frac{1}{\sqrt{2}} \cdot \cos θ - \frac{1}{\sqrt{2}} \sin θ \\ = 0 \end{aligned}$

44. The value of $\cot (\frac{π}{4} + θ) \cot (\frac{π}{4} - θ)$ is

(a) -1

(b) 0

(d) Not defined

Thinking Process

$Use formula i.e., (\cot (A + B) = \frac{\cot A \cot B - 1}{\cot A + \cot B}) and \cot (A - B) = (\frac{\cot A \cot B + 1}{\cot A - \cot B})$

Show Answer

Solution

(c)

$\begin{aligned} Given expression, (\cot \frac{π}{4} + θ) - \cot (\frac{π}{4} - θ) \\ = (\frac{\cot \frac{π}{4} \cot θ - 1}{\cot \frac{π}{4} + \cot θ}) \cdot (\frac{\cot \frac{π}{4} \cot θ + 1}{\cot θ - \cot \frac{π}{4}}) \\ = (\frac{\cot θ - 1}{\cot θ + 1}) \cdot (\frac{\cot θ + 1}{\cot θ - 1}) \\ = 1 \end{aligned}$

45. $\cos 2 θ \cos 2 φ + \sin^{2} (θ - φ) - \sin^{2} (θ + φ)$ is equal to

(a) $\sin 2 (θ + φ)$

(b) $\cos 2 (θ + φ)$

(d) $\cos 2 (θ - φ)$

Show Answer

Solution

(b) Given expression, $\cos 2 θ \cos 2 φ + \sin^{2} (θ - φ) - \sin^{2} (θ + φ)$

$\begin{aligned} = \cos 2 θ \cdot \cos 2 φ + \sin (θ - φ + θ + φ) \cdot \sin (θ - φ - θ - φ) \\ = \cos 2 θ \cdot \cos 2 φ - \sin 2 θ \cdot \sin 2 φ \\ = \cos (2 θ + 2 φ) = \cos 2 (θ + φ) \end{aligned}$

46. The value of $\cos 12^{\circ} + \cos 84^{\circ} + \cos 156^{\circ} + \cos 132^{\circ}$ is

(a) $\frac{1}{2}$

(b) 1

(d) $\frac{1}{8}$

Thinking Process

Use the formula $\cos A + \cos B = 2 \cos \frac{A + B}{2} \cdot \cos \frac{A - B}{2}$ and

$\cos A - \cos B = - 2 \sin \frac{A + B}{2} \cdot \sin \frac{A - B}{2}$ to solve this problem.

Show Answer

Solution

$= \cos 12^{\circ} + \cos 150^{\circ} + \cos 84^{\circ} + \cos 132^{\circ}$

$= 2 \cos (\frac{12^{\circ} + 150^{\circ}}{2}) \cdot \cos (\frac{12^{\circ} - 150^{\circ}}{2}) + 2 \cos (\frac{84^{\circ} + 132^{\circ}}{2}) \cdot \cos (\frac{84^{\circ} - 132^{\circ}}{2})$

$= 2 \cos 84^{\circ} \cos 72^{\circ} + 2 \cos 108^{\circ} \cdot \cos 24^{\circ}$

$= 2 \cos 84^{\circ} \cos (90^{\circ} - 18^{\circ}) + 2 \cos (90^{\circ} + 18^{\circ}) \cdot \cos 24^{\circ}$

$= 2 \cos 84^{\circ} \sin 18^{\circ} - 2 \sin 18^{\circ} \cdot \cos 24^{\circ}$

$= 2 \sin 18^{\circ} (\cos 84^{\circ} - \cos 24^{\circ})$

$= 2 \sin 18^{\circ} \cdot 2 \sin (\frac{84^{\circ} + 24^{\circ}}{2}) \cdot \sin (\frac{84^{\circ} - 24^{\circ}}{2})$

$= - 4 \sin 18^{\circ} \cdot \sin 54^{\circ} \sin 30^{\circ}$

$= - 4 \frac{\sqrt{5} - 1}{4} \cdot \cos 36^{\circ} \cdot \frac{1}{2}$

$= - (\sqrt{5} - 1) \frac{\sqrt{5} + 1}{4} \cdot \frac{1}{2} = - \frac{5 - 1}{8} = \frac{- 4}{8} = \frac{- 1}{2}$

47. If $\tan A = \frac{1}{2}$ and $\tan B = \frac{1}{3}$ , then $\tan (2 A + B)$ is equal to

(a) 1

(b) 2

(d) 4

Show Answer

Solution

Now, $\tan (2 A + B) = \frac{\tan 2 A + \tan B}{1 - \tan 2 A \cdot \tan B}$

Also, $\tan 2 A = \frac{2 \tan A}{1 - \tan^{2} A} = \frac{2 \cdot \frac{1}{2}}{1 - \frac{1}{4}} = \frac{4}{3}$

From Eq. (i), $\tan (2 A + B) = \frac{\frac{4}{3} + \frac{1}{3}}{1 - \frac{4}{3} \cdot \frac{1}{3}} = \frac{\frac{4}{3} + \frac{1}{3}}{\frac{9 - 4}{9}} = \frac{\frac{5}{3}}{\frac{5}{9}} = 3$

48. The value of $\sin \frac{π}{10} \sin \frac{13 π}{10}$ is

(a) $\frac{1}{2}$

(b) $- \frac{1}{2}$

(d) 1

Show Answer

Solution

$\begin{aligned} = - \sin \frac{π}{10} \sin \frac{3 π}{10} = - \sin 18^{\circ} \cdot \sin 54^{\circ} \\ = - \sin 18^{\circ} \cdot \cos 36^{\circ} \\ = - \frac{\sqrt{5} - 1}{4} \frac{\sqrt{5} + 1}{4} [since,put this value here] \\ = - \frac{5 - 1}{16} = - \frac{1}{4} \end{aligned}$

49. The value of $\sin 50^{\circ} - \sin 70^{\circ} + \sin 10^{\circ}$ is

(a) 1

(b) 0

(d) 2

Thinking Process

Here, use the formula i.e., $\sin A - \sin B = 2 \cos \frac{A + B}{2} \cdot \sin \frac{A - B}{2}$ also $\sin (- θ) = - \sin θ$

Show Answer

Solution

(b) Given expression, $\sin 50^{\circ} - \sin 70^{\circ} + \sin 10^{\circ}$

$\begin{aligned} = 2 \cos (\frac{50^{\circ} + 70^{\circ}}{2}) \cdot \sin (\frac{50^{\circ} - 70^{\circ}}{2} + \sin 10^{\circ}) \\ = - 2 \cos 60^{\circ} \sin 10^{\circ} + \sin 10^{\circ} \\ = - 2 \cdot \frac{1}{2} \sin 10^{\circ} + \sin 10^{\circ} = 0 \end{aligned}$

50. If $\sin θ + \cos θ = 1$ , then the value of $\sin 2 θ$ is

(a) 1

(b) $\frac{1}{2}$

(d) -1

Show Answer

Solution

On squaring both sides, we get

$\sin^{2} θ + \cos^{2} θ + 2 \sin θ \cdot \cos θ = 1$

$\Rightarrow 1 + \sin 2 θ = 1$

$∴ \sin 2 θ = 0$

51. If $α + β = \frac{π}{4}$ , then the value of $(1 + \tan α) (1 + \tan β)$ is

(a) 1

(b) 2

(d) Not defined

Thinking Process

Formula i.e., $\tan (A + B) = \frac{\tan A + \tan B}{1 - \tan A \cdot \tan B}$ to solve this problem.

Show Answer

Solution

(b) Given that, $α + β = \frac{π}{4}$

Now, $(1 + \tan α) (1 + \tan β) = 1 + \tan α + \tan β + \tan α \tan β \dots (i)$

We know that, $\tan (α + β) = \frac{\tan α + \tan β}{1 - \tan α \cdot \tan β}$

$\begin{aligned} \Rightarrow 1 = \frac{\tan α + \tan β}{1 - \tan α \cdot \tan β} . . (i) \\ \Rightarrow \tan α + \tan β = 1 - \tan α \tan β \end{aligned}$

From Eq. (i),

$\begin{aligned} (1 + \tan α) (1 + \tan β) & = 1 + 1 - \tan α \cdot \tan β + \tan α \cdot \tan β \\ = 2 \end{aligned}$

52. If $\sin θ = \frac{- 4}{5}$ and $θ$ lies in third quadrant, then the value of $\cos \frac{θ}{2}$ is

(a) $\frac{1}{5}$

(b) $- \frac{1}{\sqrt{10}}$

(d) $\frac{1}{\sqrt{10}}$

Thinking Process

Use $\cos θ = \sqrt{1 - \sin^{2} θ}$ and $\cos θ = 2 \cos^{2} \frac{θ}{2} - 1$ .

Show Answer

Solution

$\begin{aligned} \cos θ & = \sqrt{1 - \frac{16}{25}} = \sqrt{\frac{25 - 16}{25}} = \pm \frac{3}{5} \\ \cos θ & = \frac{- 3}{5} [since, θ lies in third quadrant] \\ \Rightarrow 2 \cos^{2} \frac{θ}{2} - 1 & = \frac{- 3}{5} \\ \Rightarrow 2 \cos^{2} \frac{θ}{2} & = 1 - \frac{3}{5} \\ \Rightarrow 2 \cos^{2} \frac{θ}{2} & = \frac{2}{5} \\ ∴ \cos^{\frac{θ}{2}} & = \pm \frac{1}{\sqrt{5}} \\ \Rightarrow \cos \frac{θ}{2} & = - \frac{1}{\sqrt{5}} [since, θ lies in third quadrant] \end{aligned}$

53. The number of solutions of equation $\tan x + \sec x = 2 \cos x$ lying in the interval $[0, 2 π]$ is

(a) 0

(b) 1

(d) 3

Show Answer

Solution

$\Rightarrow \tan + \sec x = 2 \cos x$

$\Rightarrow \frac{\sin x}{\cos x} + \frac{1}{\cos x} = 2 \cos x$

$\Rightarrow 1 + \sin x = 2 \cos^{2} x$

$1 + \sin x = 2 (1 - \sin^{2} x)$

$\Rightarrow 1 + \sin x = 2 - 2 \sin^{2} x$

$\Rightarrow 2 \sin^{2} x + \sin x - 1 = 0$

$\Rightarrow 2 \sin^{2} x + 2 \sin x - \sin x - 1 = 0$

$\Rightarrow 2 \sin x (\sin x + 1) - 1 (\sin x + 1) = 0$

$\Rightarrow (\sin x + 1) (2 \sin x - 1) = 0$

$\Rightarrow \sin x + 1 = 0$ or $(2 \sin x - 1) = 0$

$\Rightarrow \sin x = - 1, \sin x = \frac{1}{2}$

$∴ x = \frac{3 π}{2}, x = \frac{π}{6}$

Hence, only two solutions possible.

54. The value of $\sin \frac{π}{18} + \sin \frac{π}{9} + \sin \frac{2 π}{9} + \sin \frac{5 π}{18}$ is

(a) $\sin \frac{7 π}{18} + \sin \frac{4 π}{9}$

(b) 1

(d) $\cos \frac{π}{9} + \sin \frac{π}{9}$

Thinking Process

Here, apply the formulae i.e., $\sin A + \sin B = 2 \sin \frac{A + B}{2} \cos \frac{A - B}{2}$ .

Show Answer

Solution

(a) Given expression, $\sin \frac{π}{18} + \sin \frac{π}{9} + \sin \frac{2 π}{9} + \sin \frac{5 π}{18}$

$\begin{aligned} = \sin 10^{\circ} + \sin 20^{\circ} + \sin 40^{\circ} + \sin 50^{\circ} \\ = \sin 50^{\circ} + \sin 10^{\circ} + \sin 40^{\circ} + \sin 20^{\circ} \\ = \sin 130^{\circ} + \sin 10^{\circ} + \sin 140^{\circ} + \sin 20^{\circ} \\ = 2 \sin 70^{\circ} \cos 60^{\circ} + 2 \sin 80^{\circ} \cdot \cos 60^{\circ} [∵ \sin x + \sin y = 2 \sin \frac{x + y}{2} \cdot \cos \frac{x - y}{2}] \\ = 2 \cdot \frac{1}{2} \sin 70^{\circ} + 2 \cdot \frac{1}{2} \sin 80^{\circ} [∵ \cos 60^{\circ} = \frac{1}{2}] \\ = \sin 70^{\circ} + \sin 80^{\circ} = \sin \frac{7 π}{18} + \sin \frac{4 π}{9} \end{aligned}$

55. If $A$ lies in the second quadrant and $3 \tan A + 4 = 0$ , then the value of $2 \cot A - 5 \cos A + \sin A$ is

(a) $\frac{- 53}{10}$

(b) $\frac{23}{10}$

(d) $\frac{7}{10}$

Thinking Process

Use the formulae i.e., $\sec A = \sqrt{1 + \tan^{2} A}$ and $\sin A = \sqrt{1 - \cos^{2} A}, \sec A = \frac{1}{\cos A}$ and $\tan A = \frac{1}{\cot A}$ .

Show Answer

Solution (b)

$\begin{aligned} Given equation, 3 \tan A + 4 = 0 \\ \Rightarrow 3 \tan A = - 4 \\ \Rightarrow \tan A = \frac{- 4}{3} \\ \Rightarrow \cot A = \frac{- 3}{4} \\ \Rightarrow \sec A = \sqrt{1 + \frac{16}{9}} = \sqrt{\frac{25}{9}} = \pm \frac{5}{3} [since, A lies in second quadrant] \\ \Rightarrow \sec A = \frac{- 5}{3} \\ \cos A = \frac{- 3}{5} \\ \sin A = \sqrt{1 - \frac{9}{25}} = \frac{\sqrt{25 - 9}}{25} = \pm \frac{4}{5} \\ \sin A = \frac{4}{5} \end{aligned} [since, A lies in second quadrant]$

$\begin{aligned} ∴ 2 \cot A - 5 \cos A + \sin A & = 2 \frac{- 3}{4} - 5 \frac{- 3}{5} + \frac{4}{5} \\ = \frac{- 6}{4} + 3 + \frac{4}{5} \\ = \frac{- 30 + 60 + 16}{20} = \frac{46}{20} \\ = \frac{23}{10} \end{aligned}$

56. The value of $\cos^{2} 48^{\circ} - \sin^{2} 12^{\circ}$ is

(a) $\frac{\sqrt{5} + 1}{8}$

(b) $\frac{\sqrt{5} - 1}{8}$

(d) $\frac{\sqrt{5} + 1}{2 \sqrt{2}}$

Show Answer

Solution

(a) Given expression, $\cos^{2} 48^{\circ} - \sin^{2} 12^{\circ}$

$\begin{aligned} = \cos (48^{\circ} + 12^{\circ}) - \cos (48^{\circ} - 12^{\circ}) \\ = \cos 60^{\circ} \cdot \cos 36^{\circ} \\ = \frac{1}{2} \cdot \frac{\sqrt{5} + 1}{4} \\ = \frac{\sqrt{5} + 1}{8} \end{aligned}$

57. If $\tan α = \frac{1}{7}$ and $\tan β = \frac{1}{3}$ , then $\cos 2 α$ is equal to

(a) $\sin 2 β$

(b) $\sin 4 β$

(d) $\cos 2 β$

Thinking Process

Use $\cos 2 α = \frac{1 - \tan^{2} α}{1 + \tan^{2} α}$ and $\sin 2 α = \frac{2 \tan α}{1 + \tan^{2} α}$

Show Answer

Solution

(b) Given that,

$\begin{aligned} \cos 2 α & = \frac{1 - \frac{1}{49}}{1 + \frac{1}{49}} = \frac{\frac{48}{49}}{\frac{50}{49}} \\ = \frac{48}{50} = \frac{24}{25} \\ \Rightarrow \cos 2 α & = \frac{24}{25} . . (i) \\ We know that, \sin 4 β & = \frac{2 \tan 2 β}{1 + \tan^{2} 2 β} . . (i i) \\ and \tan 2 β & = \frac{2 \tan^{2}}{1 - \tan^{2} β} = \frac{2 \times \frac{1}{3}}{1 - \frac{1}{9}} \\ = \frac{2}{\frac{3}{9}} = \frac{2 \times 9}{3 \times 8} = \frac{3}{4} \end{aligned}$

$\tan = \frac{1}{7} and \tan β = \frac{1}{3}$

From Eq, (ii),

$\sin 4 β = \frac{2 \times \frac{3}{4}}{1 + \frac{9}{16}} = \frac{\frac{6}{4}}{\frac{25}{16}} = \frac{6 \times 16}{4 \times 25}$

$\Rightarrow \sin 4 β = \frac{24}{25}$

$\Rightarrow \sin 4 β = \cos 2 α$

$∴ \cos 2 α = \sin 4 β$

58. If $\tan θ = \frac{a}{b^{'}}$ , then $b \cos 2 θ + a \sin 2 θ$ is equal to

(a) a

(b) $b$

(d) None of these

Show Answer

Solution

(b) Given that, $\tan θ = \frac{a}{b}$

$\begin{aligned} ∴ b \cos 2 θ + a \sin 2 θ & = b (\frac{1 - \tan^{2} θ}{1 + \tan^{2} θ}) + a (\frac{2 \tan θ}{1 + \tan^{2} θ}) \\ = b (\frac{1 - \frac{a^{2}}{b^{2}}}{1 + \frac{a^{2}}{b^{2}}}) + a (\frac{\frac{2 a}{b}}{1 + \frac{a^{2}}{b^{2}}}) \\ = b (\frac{b^{2} - a^{2}}{b^{2} + a^{2}}) + \frac{2 a^{2} b}{a^{2} + b^{2}} \\ = \frac{b}{a^{2} + b^{2}} [b^{2} - a^{2} + 2 a^{2}] = \frac{(a^{2} + b^{2}) b}{(a^{2} + b^{2})} \\ = b \end{aligned}$

59. If for real values of $x, \cos θ = x + \frac{1}{x}$ , then

(a) $θ$ is an acute angle

(b) $θ$ is right angle

(d) No value of $θ$ is possible

Thinking Process

The quadratic equation $a x^{2} + b x + c = 0$ has real roots, then $b^{2} - 4 a c = 0$ , use this condition to solve the above problem.

Show Answer

Solution

(d)

$\begin{aligned} Here, \cos θ & = x + \frac{1}{x} \\ \Rightarrow \cos θ & = \frac{x^{2} + 1}{x} \\ x^{2} - x \cos θ + 1 & = 0 \end{aligned}$

For real value of $x, (- \cos θ)^{2} - 4 \times 1 \times 1 = 0$

$\begin{aligned} \cos^{2} θ & = 4 \\ \cos θ & = \pm 2 \end{aligned}$

which is not possible.

$[∵ - 1 \leq \cos θ \leq 1]$

Fillers

60. The value of $\frac{\sin 50^{\circ}}{\sin 130^{\circ}}$ is ……

Show Answer

Solution

Here,

$\begin{aligned} \frac{\sin 50^{\circ}}{\sin 130^{\circ}} & = \frac{\sin (180^{\circ} - 130^{\circ})}{\sin 130^{\circ}} \\ = \frac{\sin 130^{\circ}}{\sin 130^{\circ}} = 1 \end{aligned}$

61. If $k = \sin (\frac{π}{18}) \sin (\frac{5 π}{18}) \sin (\frac{7 π}{18})$ , then the numerical value of $k$ is ……

Show Answer

Solution Here, $k = \sin (\frac{π}{18}) \sin (\frac{5 π}{18}) \sin (\frac{7 π}{18})$

$= \sin 10^{\circ} \sin 50^{\circ} \sin 70^{\circ}$

$\begin{aligned} = \sin 10^{\circ} \cos 40^{\circ} \cdot \cos 20^{\circ} \\ = \frac{1}{2} \sin 10^{\circ} [2 \cos 40^{\circ} \cdot \cos 20^{\circ}] \\ = \frac{1}{2} \sin 10^{\circ} [\cos 60^{\circ} + \cos 20^{\circ}] [∵ 2 \cos x \cdot \cos y = \cos (x + y) + \cos (x - y)] \\ = \frac{1}{2} \sin 10^{\circ} \cdot \frac{1}{2} + \frac{1}{2} \sin 10^{\circ} \cos 20^{\circ} \\ = \frac{1}{4} \sin 10^{\circ} + \frac{1}{4} [\sin 30^{\circ} - \sin 10^{\circ}] \\ = \frac{1}{8} \end{aligned}$

62. If $\tan A = \frac{1 - \cos θ}{\sin B}$ , then $\tan 2 A =$ ……

Thinking Process

Use $\cos θ = 1 - 2 \sin^{2} \frac{θ}{2}$ and $\tan 2 θ = \frac{2 \tan θ}{1 - \tan^{2} θ}$ .

Show Answer

Solution

Given that,

$\begin{aligned} \tan A & = \frac{1 - \cos B}{\sin B} \\ = \frac{1 - 1 + 2 \sin^{2} \frac{B}{2}}{2 \sin \frac{B}{2} \cdot \cos \frac{B}{2}} = \tan \frac{B}{2} \end{aligned}$

$Now, \tan 2 A = \frac{2 \tan A}{1 - \tan^{2} A}$

$\Rightarrow \tan 2 A = \frac{2 \cdot \tan \frac{B}{2}}{1 - \tan^{2} \frac{B}{2}}$

$\Rightarrow \tan 2 A = \tan B$

63. If $\sin x + \cos x = a$ , then

(i) $\sin^{6} x + \cos^{6} x = \dots \dots .$

(ii) $| \sin x - \cos x | = \dots \dots$

Show Answer

Solution

Given that, $\sin x + \cos x = a$

On squaring both sides, we get

$\begin{aligned} (\sin x + \cos x)^{2} = (a)^{2} \\ \Rightarrow \sin^{2} x + \cos^{2} x + 2 \sin x \cos x = a^{2} \\ \Rightarrow \sin x \cdot \cos x = \frac{1}{2} (a^{2} - 1) \\ (i) & \sin^{6} x + \cos^{6} x = (s i n^{2} x)^{3} + (\cos^{2} x)^{3} \\ = (\sin^{2} x + \cos^{2} x) (\sin^{4} x - \sin^{2} x \cos^{2} x + \cos^{4} x) \\ = \sin^{4} x + \cos^{4} x - \frac{1}{4} (a^{2} - 1)^{2} \\ = (\sin^{2} x + \cos^{2} x)^{2} - 2 \sin^{2} x \cos^{2} x - \frac{1}{4} (a^{2} - 1)^{2} \\ = 1 - 2 \cdot \frac{1}{4} (a^{2} - 1)^{2} - \frac{1}{4} (a^{2} - 1)^{2} = \frac{1}{4} [4 - 3 (a^{2} - 1)^{2}] \end{aligned}$

(ii) $| \sin x - \cos x | = \sqrt{(\sin x - \cos x)^{2}}$

$\begin{aligned} = \sqrt{\sin^{2} x + \cos^{2} x - 2 \sin x \cos x} \\ = \sqrt{1 - 2 \frac{1}{2} (a^{2} - 1)} = \sqrt{1 - a^{2} + 1} = \sqrt{2 - a^{2}} \end{aligned}$

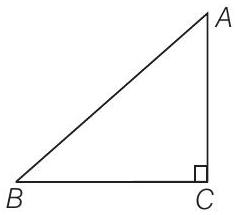
64. In right angled $△ A B C$ with $∠ C = 90^{\circ}$ the equation whose roots $a r e \tan A$ and $\tan B$ is ……

Show Answer

Solution

In right angled $△ A B C, ∠ C = 90^{\circ}$

$\begin{aligned} ∴ \tan (A + B) = \frac{\tan A + \tan B}{1 - \tan A \tan B} \\ \Rightarrow \frac{1}{0} = \frac{\tan A + \tan B}{1 - \tan A \tan B} \\ \Rightarrow \tan A \tan B = 1 \\ \tan A + \tan B = \frac{\sin A}{\cos A} + \frac{\sin B}{\cos B} \\ = \frac{\sin A}{\cos A} + \frac{\cos A}{\sin A} \\ = \frac{\sin^{2} A + \cos^{2} A}{\sin A \cdot \cos A} \\ = \frac{1}{\sin A \cdot \cos A} = \frac{2}{2 \cdot \sin A \cdot \cos A} \end{aligned}$

$\begin{matrix} = \frac{\sin A}{\cos A} + \frac{\sin (90^{\circ} - A)}{\cos (90^{\circ} - A)} & [∵ ∠ C = 90^{\circ}, ∠ B = 90^{\circ} - A] \\ = \frac{\sin A}{\cos A} + \frac{\cos A}{\sin A} \\ = \frac{\sin^{2} A + \cos^{2} A}{\sin A \cdot \cos A} \\ = \frac{1}{\sin A \cdot \cos A} = \frac{2}{2 \cdot \sin A \cdot \cos A} \\ = \frac{2}{\sin 2 A} & [∵ \sin 2 x = 2 \sin x \cos x] \end{matrix}$

So, the required equation is $x^{2} - \frac{2}{\sin A} x + 1$ .

$∵ \sin 2 x = 2 \sin x \cos x$

65. $3 (\sin x - \cos x)^{4} + 6 (\sin x + \cos x)^{2} + 4 (\sin^{6} x + \cos^{6} x) =$ ……

Thinking Process

Use formulae i.e., $(a^{3} + b^{3}) = (a + b) (a^{2} - a b + b^{2})$ and $a^{2} + b^{2} = (a + b)^{2} - 2 a b$ .

Show Answer

Solution

Given expression, $3 (\sin x - \cos x)^{4} + 6 (\sin x + \cos x)^{2} + 4 (\sin^{6} x + \cos^{6} x)$

$\begin{aligned} = 3 [\sin^{2} x + \cos^{2} x - 2 \sin x \cos x]^{2} + 6 [\sin^{2} x + \cos^{2} x + 2 \cdot \sin x \cdot \cos x] \\ + 4 [(\sin^{2} x)^{3} + (\cos^{2} x)^{3}] \\ = 3 (1 - \sin 2 x)^{2} + 6 (1 + \sin 2 x) + 4 [(\sin^{2} + \cos^{2} x) (\sin^{4} x - \sin x \cos^{2} x + \cos^{4} x) . \\ = 3 (1 + \sin^{2} 23 x - 2 \sin 2 x) + 6 + 6 \sin 2 x + 4 [(\sin^{2} x + \cos^{2} x)^{2} 3 \sin x \cos^{2} x] \\ = 3 + 3 \sin^{2} 2 x - 6 \sin 2 x + 6 + 6 \sin 2 x \\ = 4 - 3 \sin^{2} 2 x = 13 \end{aligned}$

66. Given $x > 0$ , the value of $f (x) = - 3 \cos \sqrt{3 + x + x^{2}}$ lie in the interval ……

Show Answer

Solution

Given function, $f (x) = - 3 \cos \sqrt{3 + x + x^{2}}$

$\begin{matrix} We know that, & - 1 \leq \cos x \leq 1 \\ \Rightarrow & - 3 \leq 3 \cos x \leq 3 \\ \Rightarrow & 3 \geq - 3 \cos x \geq - \\ \Rightarrow & - 3 \leq - 3 \cos x \leq 3 \end{matrix}$

So, the value of $f (x)$ lies in $[- 3, 3]$ .

67. The maximum distance of a point on the graph of the function $y = \sqrt{3} \sin x + \cos x$ from $X$ -axis is ……

Show Answer

Solution

Given that, $y = \sqrt{3} \sin x + \cos x$

$\begin{aligned} y & = 2 [\frac{\sqrt{3}}{2} \sin x + \frac{1}{2} \cos x] \\ = 2 [\sin x \cdot \cos \frac{π}{6} + \cos x \sin \frac{π}{6}] \\ = 2 \sin (x + π / 6) \end{aligned}$

Graph of $y = 2 \sin x$

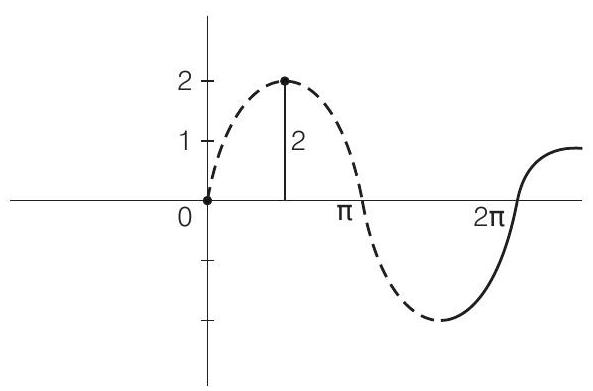
Hence, the maximum distance is 2 units.

True/False

68. In each of the questions 68 to 75 , state whether the statements is True or False? Also, give justification.

Thinking Process

$If \tan A = \frac{1 - \cos B}{\sin B}, then \tan 2 A = \tan B$

Show Answer

Solution

True

$\begin{aligned} Given that, & \tan A = \frac{1 - \cos B}{\sin B} = \frac{1 - 1 + 2 \sin^{2} \frac{B}{2}}{2 \sin \frac{B}{2} \cdot \cos \frac{B}{2}} = \tan \frac{B}{2} \\ Now, & \tan 2 A = \frac{2 \tan A}{1 - \tan^{2} A} = \frac{2 \cdot \tan \frac{B}{2}}{1 - \tan^{2} \frac{B}{2}} = \tan B \end{aligned}$

69. The equality $\sin A + \sin 2 A + \sin 3 A = 3$ holds for some real value of $A$ .

Show Answer

Solution

False

Given that, $\sin A + \sin 2 A + \sin 3 A = 3$

It is possible only if $\sin A, \sin 2 A, \sin 3 A$ each has a value one because maximum value of $\sin A$ is a certain angle is 1 . Which is not possible because angle are different.

70. $\sin 10^{\circ}$ is greater than $\cos 10^{\circ}$ .

Show Answer

Solution

False

$\sin 10^{\circ} = \sin (90^{\circ} - 80^{\circ})$

$\sin 10^{\circ} = \cos 80^{\circ}$

$∵ \cos 80^{\circ} < \cos 10^{\circ}$

$Hence, \sin 10^{\circ} < \cos 10^{\circ}$

71. $\cos \frac{2 π}{15} \cos \frac{4 π}{15} \cos \frac{8 π}{15} \cos \frac{16 π}{15} = \frac{1}{16}$

Show Answer

Solution

True

$\begin{aligned} LHS & = \cos \frac{2 π}{15} \cos \frac{4 π}{15} \cos \frac{8 π}{15} \cos \frac{16 π}{15} \\ = \cos 24^{\circ} \cos 48^{\circ} \cos 96^{\circ} \cos 192^{\circ} \\ = \frac{1}{16 \sin 24^{\circ}} [(2 \sin 24^{\circ} \cos 24^{\circ}) (2 \cos 48^{\circ}) (2 \cos 96^{\circ}) (2 \cos 192^{\circ})] \\ = \frac{1}{16 \sin 24^{\circ}} [2 \sin 48^{\circ} \cos 48^{\circ} (2 \cos 96^{\circ}) (2 \cos 192^{\circ})] \\ = \frac{1}{16 \sin 24^{\circ}} [(2 \sin 96^{\circ} \cos 96^{\circ}) (2 \cos 192^{\circ})] \\ = \frac{1}{16 \sin 24^{\circ}} [2 \sin 192^{\circ} \cos 192^{\circ}) \\ = \frac{1}{16 \sin 24^{\circ}} \sin 384^{\circ} = \frac{\sin (360^{\circ} + 24^{\circ})}{16 \sin 24^{\circ}} \\ = \frac{1}{16} = R H S Hence proved. \end{aligned}$

72. One value of $θ$ which satisfies the equation $\sin^{4} θ - 2 \sin^{2} θ - 1$ lies between 0 and $2 π$ .

Show Answer

Solution

False

Given equation, $\sin^{4} θ - 2 \sin^{2} θ - 1 = 0$

$\Rightarrow \sin^{2} θ = \frac{2 \pm \sqrt{4 + 4}}{2}$

$\Rightarrow \sin^{2} θ = \frac{2 \pm 2 \sqrt{2}}{2}$

$\Rightarrow \sin^{2} θ = (1 + \sqrt{2})$ or $(1 - \sqrt{2}) \Rightarrow - 1 \leq \sin θ \leq 1$

$\Rightarrow \sin^{2} θ \leq 1$

$∵ \sin^{2} θ = \sqrt{2 + 1}$ or $(1 - \sqrt{2})$

which is not possible.

73. If $c o s e c x = 1 + \cot x$ , then $x = 2 n π, 2 n π + \frac{π}{2}$

Show Answer

Solution

True

Given that,

$\begin{aligned} c o s e c x & = 1 + \cot x \\ \frac{1}{\sin x} & = 1 + \frac{\cos x}{\sin x} \Rightarrow \frac{1}{\sin x} = \frac{\sin x + \cos x}{\sin x} \end{aligned}$

$\Rightarrow$

$\Rightarrow \sin x + \cos x = 1$

$\Rightarrow \frac{1}{\sqrt{2}} \cdot \sin x + \frac{1}{\sqrt{2}} \cdot \cos x = \frac{1}{\sqrt{2}}$

$\Rightarrow \sin \frac{π}{4} \sin x + \cos x \cos \frac{π}{4} = \frac{1}{\sqrt{2}}$

$\Rightarrow \cos (x - \frac{π}{4}) = \cos \frac{π}{4}$

$∴ x - \frac{π}{4} = 2 n π \pm \frac{π}{4}$

$\begin{aligned} For positive sign, & x = 2 n π + \frac{π}{4} + \frac{π}{4} = 2 n π + \frac{π}{2} \\ For negative sign, & x = 2 n π - \frac{π}{4} + \frac{π}{4} = 2 n π \end{aligned}$

74. If $\tan θ + \tan 2 θ + \sqrt{3} \tan θ \tan 2 θ = \sqrt{3}$ , then $θ = \frac{n π}{3} + \frac{π}{9}$ .

Show Answer

Solution

True

$\begin{aligned} \tan θ + \tan 2 θ + \sqrt{3} \tan θ \tan 2 θ = \sqrt{3} \\ \Rightarrow \tan θ + \tan 2 θ = \sqrt{3} - \sqrt{3} \tan θ \tan 2 θ \\ \Rightarrow \tan θ + \tan 2 θ = \sqrt{3} (1 - \tan θ \tan 2 θ) \\ \Rightarrow \frac{\tan θ + \tan 2 θ}{1 - \tan θ \tan 2 θ} = \sqrt{3} \\ \Rightarrow \tan (θ + 2 θ) = \tan \frac{π}{3} \Rightarrow \tan 3 θ = \tan \frac{π}{3} \\ ∴ 3 θ = n π + \frac{π}{3} \\ θ = \frac{n π}{3} + \frac{π}{9} \end{aligned}$

75. If $\tan (π \cos θ) = \cot (π \sin θ)$ , then $\cos θ - \frac{π}{4} = \pm \frac{1}{2 \sqrt{2}}$ .

Thinking Process

Use the formulae i.e., $\tan \frac{π}{2} - θ = \cot θ$ and $\cos (A - B) = \cos A \cos B + \sin A \sin B$ .

Show Answer

Solution

True

$We have, \tan (π \cos θ) = \cot (π \sin θ)$

$\Rightarrow \tan (π \cos θ) = \tan \frac{π}{2} - (π \sin θ)$

$\Rightarrow π \cos = \frac{π}{2} - π \sin θ$

$\Rightarrow π (\sin θ + \cos θ) = \frac{π}{2}$

$\Rightarrow \sin θ + \cos θ = \frac{1}{2}$

$\Rightarrow \frac{1}{\sqrt{2}} \cdot \sin θ + \frac{1}{\sqrt{2}} \cdot \cos θ = \frac{1}{2 \sqrt{2}}$

$\Rightarrow \sin θ \cdot \sin \frac{π}{4} + \cos θ \cdot \cos \frac{π}{4} = \frac{1}{2 \sqrt{2}}$

$∴ \cos θ - \frac{π}{4} = \frac{1}{2 \sqrt{2}}$

76. In the following match each item given under the Column I to its correct answer given under the Column II.

	Column I		Column II
(i)	$\sin (x + y) \sin (x - y)$	(a)	$\cos^{2} x - \sin^{2} y$
(ii)	$\cos (x + y) \cos (x - y)$	(b)	$1 - \tan θ / 1 + \tan θ$
(iii)	$\cot (\frac{π}{4} + θ)$	(c)	$1 + \tan θ / 1 - \tan θ$
(iv)	$\tan (\frac{π}{4} + θ)$	(d)	$\sin^{2} x - \sin^{2} y$

Show Answer

Solution

(i) $\sin (x + y) \sin (x - y) = \sin^{2} x - \sin^{2} y$

(ii) $\cos (x + y) \cos (x - y) = \cos^{2} x - \sin^{2} y$

(iii) $\cot \frac{π}{4} + θ = \frac{\cot \frac{π}{4} \cot θ - 1}{\cot \frac{π}{4} + \cot θ}$

$= \frac{- 1 + \cot θ}{1 + \cot θ} = \frac{1 - \tan θ}{1 + \tan θ}$

(iv) $\tan \frac{π}{4} + θ = \frac{\tan \frac{π}{4} + \tan θ}{1 - \tan \frac{π}{4} \tan θ} = \frac{1 + \tan θ}{1 - \tan θ}$

Hence, the correct mathes are (i) $\rarr$ (d), (ii) $\rarr$ (a), (iii) $\rarr$ (b), (iv) $\rarr$ (c).

Relations and Functions

Maths (Class-11) | NCERT Exemplar

Trigonometric Functions

Short Answer Type Questions

Long Answer Type Questions

Objective Type Questions

Fillers

True/False

Table of Contents

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Maths (Class-11) | NCERT Exemplar

Trigonometric Functions

Short Answer Type Questions

Long Answer Type Questions

Objective Type Questions

Fillers

True/False

Table of Contents

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu