APPLICATION OF DERIVATIVES

With the Calculus as a key, Mathematics can be successfully applied to the explanation of the course of Nature." - WHITEHEAD

6.1 Introduction

In Chapter 5, we have learnt how to find derivative of composite functions, inverse trigonometric functions, implicit functions, exponential functions and logarithmic functions. In this chapter, we will study applications of the derivative in various disciplines, e.g., in engineering, science, social science, and many other fields. For instance, we will learn how the derivative can be used (i) to determine rate of change of quantities, (ii) to find the equations of tangent and normal to a curve at a point, (iii) to find turning points on the graph of a function which in turn will help us to locate points at which largest or smallest value (locally) of a function occurs. We will also use derivative to find intervals on which a function is increasing or decreasing. Finally, we use the derivative to find approximate value of certain quantities.

6.2 Rate of Change of Quantities

Recall that by the derivative $\\ \frac{ds}{dt} $, we mean the rate of change of distance $s$ with respect to the time $t$. In a similar fashion, whenever one quantity $y$ varies with another quantity $x$, satisfying some rule $y=f(x)$, then $\frac{d y}{d x}$ (or $f^{\prime}(x)$ ) represents the rate of change of $y$ with respect to $x$ and $\frac{d y}{d x} _{x=x_0}(.$ or $.f^{\prime}(x_0))$ represents the rate of change of $y$ with respect to $x$ at $x=x_0$.

Further, if two variables $x$ and $y$ are varying with respect to another variable $t$, i.e., if $x=f(t)$ and $y=g(t)$, then by Chain Rule

$ \frac{d y}{d x}=\frac{d y}{d t} / \frac{d x}{d t}, \text{ if } \frac{d x}{d t} \neq 0 $

Thus, the rate of change of $y$ with respect to $x$ can be calculated using the rate of change of $y$ and that of $x$ both with respect to $t$.

Let us consider some examples.

Example 1 Find the rate of change of the area of a circle per second with respect to its radius $r$ when $r=5 cm$.

Solution The area A of a circle with radius $r$ is given by $A=\pi r^{2}$. Therefore, the rate of change of the area A with respect to its radius $r$ is given by $\frac{d A}{d r}=\frac{d}{d r}(\pi r^{2})=2 \pi r$.

When $r=5 cm, \frac{d A}{d r}=10 \pi$. Thus, the area of the circle is changing at the rate of $10 \pi cm^{2} / s$.

Example 2 The volume of a cube is increasing at a rate of 9 cubic centimetres per second. How fast is the surface area increasing when the length of an edge is 10 centimetres?

Solution Let $x$ be the length of a side, $V$ be the volume and $S$ be the surface area of the cube. Then, $V=x^{3}$ and $S=6 x^{2}$, where $x$ is a function of time $t$.

Now

$ \frac{d V}{d t}=9 cm^{3} / s \text{ (Given) } $

Therefore

$ 9=\frac{d V}{d t}=\frac{d}{d t}(x^{3})=\frac{d}{d x}(x^{3}) \cdot \frac{d x}{d t} \quad(\text{ By Chain Rule }) $

$ =3 x^{2} \cdot \frac{d x}{d t} $

or

$ \frac{d x}{d t}=\frac{3}{x^{2}} $

Now

$ \begin{matrix} \frac{d S}{d t} & =\frac{d}{d t}(6 x^{2})=\frac{d}{d x}(6 x^{2}) \cdot \frac{d x}{d t} & (\text{ By Chain Rule }) \\ & =12 x \cdot(\frac{3}{x^{2}})=\frac{36}{x} & \end{matrix} $

Hence, when

$ x=10 cm, \frac{d S}{d t}=3.6 cm^{2} / s $

Example 3 A stone is dropped into a quiet lake and waves move in circles at a speed of $4 cm$ per second. At the instant, when the radius of the circular wave is $10 cm$, how fast is the enclosed area increasing?

Solution The area $A$ of a circle with radius $r$ is given by $A=\pi r^{2}$. Therefore, the rate of change of area A with respect to time $t$ is

$ \frac{d A}{d t}=\frac{d}{d t}(\pi r^{2})=\frac{d}{d r}(\pi r^{2}) \cdot \frac{d r}{d t}=2 \pi r \frac{d r}{d t} $

It is given that

$ \frac{d r}{d t}=4 cm / s $

Therefore, when $r=10 cm, \quad \frac{d A}{d t}=2 \pi(10)(4)=80 \pi$

Thus, the enclosed area is increasing at the rate of $80 \pi cm^{2} / s$, when $r=10 cm$.

Note $\frac{d y}{d x}$ is positive if $y$ increases as $x$ increases and is negative if $y$ decreases as $x$ increases.

Example 4 The length $x$ of a rectangle is decreasing at the rate of $3 cm /$ minute and the width $y$ is increasing at the rate of $2 cm /$ minute. When $x=10 cm$ and $y=6 cm$, find the rates of change of (a) the perimeter and (b) the area of the rectangle.

Solution Since the length $x$ is decreasing and the width $y$ is increasing with respect to time, we have

$ \frac{d x}{d t}=-3 cm / min \quad \text{ and } \quad \frac{d y}{d t}=2 cm / min $

(a) The perimeter $P$ of a rectangle is given by

$ P=2(x+y) $

Therefore

$ \frac{d P}{d t}=2 \frac{d x}{d t}+\frac{d y}{d t}=2(-3+2)=-2 cm / min $

(b) The area $A$ of the rectangle is given by

$ A=x \cdot y $

Therefore

$ \begin{aligned} \frac{d A}{d t} & =\frac{d x}{d t} \cdot y+x \cdot \frac{d y}{d t} \\ & =-3(6)+10(2) \quad(\text{ as } x=10 cm \text{ and } y=6 cm) \\ & =2 cm^{2} / min \end{aligned} $

Example 5 The total cost $C(x)$ in Rupees, associated with the production of $x$ units of an item is given by

$ C(x)=0.005 x^{3}-0.02 x^{2}+30 x+5000 $

Find the marginal cost when 3 units are produced, where by marginal cost we mean the instantaneous rate of change of total cost at any level of output.

Solution Since marginal cost is the rate of change of total cost with respect to the output, we have

Marginal

$ \begin{aligned} cost(MC) & =\frac{d C}{d x}=0.005(3 x^{2})-0.02(2 x)+30 \\ x=3, MC & =0.015(3^{2})-0.04(3)+30 \\ & =0.135-0.12+30=30.015 \end{aligned} $

When

Hence, the required marginal cost is ₹ 30.02 (nearly).

Example 6 The total revenue in Rupees received from the sale of $x$ units of a product is given by $R(x)=3 x^{2}+36 x+5$. Find the marginal revenue, when $x=5$, where by marginal revenue we mean the rate of change of total revenue with respect to the number of items sold at an instant.

Solution Since marginal revenue is the rate of change of total revenue with respect to the number of units sold, we have

Marginal Revenue

$ \begin{aligned} (MR) & =\frac{d R}{d x}=6 x+36 \\ x & =5, MR=6(5)+36=66 \end{aligned} $

Hence, the required marginal revenue is ₹ 66 .

EXERCISE 6.1

1. Find the rate of change of the area of a circle with respect to its radius $r$ when

$\quad\quad$(a) $r=3 cm$ $\quad\quad$ (b) $r=4 cm$

Solution

The area of a circle ( $A$ ) with radius $(r)$ is given by,

$A=\pi r^{2}$

Now, the rate of change of the area with respect to its radius is given by,

$\frac{d A}{d r}=\frac{d}{d r}(\pi r^{2})=2 \pi r$

1. When $r=3 cm$,

$\frac{d A}{d r}=2 \pi(3)=6 \pi$

Hence, the area of the circle is changing at the rate of $6 cm^{2} / s$ when its radius is $3 cm$.

2. When $r=4 cm$,

$\frac{d A}{d r}=2 \pi(4)=8 \pi$

Hence, the area of the circle is changing at the rate of $8 cm^{2} / s$ when its radius is $4 cm$.

2. The volume of a cube is increasing at the rate of $8 cm^{3} / s$. How fast is the surface area increasing when the length of an edge is $12 cm$ ?

Solution

Let $x$ be the length of a side, $V$ be the volume, and $s$ be the surface area of the cube.

Then, $V=x^{3}$ and $S=6 x^{2}$ where $x$ is a function of time $t$.

It is given that $\frac{d V}{d t}=8 cm^{3} / s$.

Then, by using the chain rule, we have:

$ \therefore=\frac{d V}{d t}=\frac{d}{d t}(x^{3})=\frac{d}{d x}(x^{3}) \cdot \frac{d x}{d t}=3 x^{2} \cdot \frac{d x}{d t} $

$ \begin{equation*} \Rightarrow \frac{d x}{d t}=\frac{8}{3 x^{2}} \tag{1} \end{equation*} $

$ \begin{aligned} & \text{ Now, } \frac{d S}{d t}=\frac{d}{d t}(6 x^{2})=\frac{d}{d x}(6 x^{2}) \cdot \frac{d x}{d t} \quad \text{ [By chain rule] } \\ & =12 x \cdot \frac{d x}{d t}=12 x \cdot(\frac{8}{3 x^{2}})=\frac{32}{x} \end{aligned} $

Hence, if the length of the edge of the cube is $12 cm$, then the surface area is increasing

at the rate of $\frac{8}{3} cm^{2} / s$.

3. The radius of a circle is increasing uniformly at the rate of $3 cm / s$. Find the rate at which the area of the circle is increasing when the radius is $10 cm$.

Solution

The area of a circle $(A)$ with radius $(r)$ is given by,

$A=\pi r^{2}$

Now, the rate of change of area $(A)$ with respect to time $(t)$ is given by,

$\frac{d A}{d t}=\frac{d}{d t}(\pi r^{2}) \cdot \frac{d r}{d t}=2 \pi r \frac{d r}{d t} \quad$ [By chain rule]

It is given that,

$\frac{d r}{d t}=3 cm / s$ $\therefore \frac{d A}{d t}=2 \pi r(3)=6 \pi r$

Thus, when $r=10 cm$,

$\frac{d A}{d t}=6 \pi(10)=60 \pi cm^{2} / s$

Hence, the rate at which the area of the circle is increasing when the radius is $10 cm$ is $60 п cm^{2} / s$.

4. An edge of a variable cube is increasing at the rate of $3 cm / s$. How fast is the volume of the cube increasing when the edge is $10 cm$ long?

Solution

Let $x$ be the length of a side and $V$ be the volume of the cube. Then,

$V=x^{3}$.

$\therefore \frac{d V}{d t}=3 x^{2} \cdot \frac{d x}{d t}$ (By chain rule)

It is given that,

$\frac{d x}{d t}=3 cm / s$

$\therefore \frac{d V}{d t}=3 x^{2}(3)=9 x^{2}$

Thus, when $x=10 cm$,

$\frac{d V}{d t}=9(10)^{2}=900 cm^{3} / s$

Hence, the volume of the cube is increasing at the rate of $900 cm^{3} / s$ when the edge is 10 $cm$ long.

5. A stone is dropped into a quiet lake and waves move in circles at the speed of $5 cm / s$. At the instant when the radius of the circular wave is $8 cm$, how fast is the enclosed area increasing?

Solution

The area of a circle (A) with radius $(r)$ is given by $A=\pi r^{2}$.

Therefore, the rate of change of area $(A)$ with respect to time $(t)$ is given by,

$\frac{d A}{d t}=\frac{d}{d t}(\pi r^{2})=\frac{d}{d r}(\pi r^{2}) \frac{d r}{d t}=2 \pi r \frac{d r}{d t}$ [By chain rule]

It is given that $\frac{d r}{d t}=5 cm / s$.

Thus, when $r=8 cm$,

$\frac{d A}{d t}=2 \pi(8)(5)=80 \pi$

Hence, when the radius of the circular wave is $8 cm$, the enclosed area is increasing at the rate of $80 \pi cm^{2} / s$.

6. The radius of a circle is increasing at the rate of $0.7 cm / s$. What is the rate of increase of its circumference?

Solution

The circumference of a circle $(C)$ with radius $(r)$ is given by $C=2 \pi r$.

Therefore, the rate of change of circumference (C) with respect to time $(t)$ is given by, $\frac{d C}{d t}=\frac{d C}{d r} \cdot \frac{d r}{d t}$ (By chain rule) $=\frac{d}{d r}(2 \pi r) \frac{d r}{d t}$

$=2 \pi \cdot \frac{d r}{d t}$

It is given that $\frac{d r}{d t}=0.7 cm / s$.

Hence, the rate of increase of the circumference is $2 \pi(0.7)=1.4 \pi cm / s$.

7. The length $x$ of a rectangle is decreasing at the rate of $5 cm /$ minute and the width $y$ is increasing at the rate of $4 cm /$ minute. When $x=8 cm$ and $y=6 cm$, find the rates of change of (a) the perimeter, and (b) the area of the rectangle.

Solution

Since the length $(x)$ is decreasing at the rate of $5 cm /$ minute and the width $(y)$ is increasing at the rate of $4 cm /$ minute, we have:

$\frac{d x}{d t}=-5 cm / min$ and $\frac{d y}{d t}=4 cm / min$

(a) The perimeter $(P)$ of a rectangle is given by,

$P=2(x+y)$

$\therefore \frac{d P}{d t}=2(\frac{d x}{d t}+\frac{d y}{d t})=2(-5+4)=-2 cm / min$

Hence, the perimeter is decreasing at the rate of $2 cm / min$.

(b) The area (A) of a rectangle is given by,

$A=x \times y$

$\therefore \frac{d A}{d t}=\frac{d x}{d t} \cdot y+x \cdot \frac{d y}{d t}=-5 y+4 x$

When $x=8 cm$ and $y=6 cm, \frac{d A}{d t}=(-5 \times 6+4 \times 8) cm^{2} / min=2 cm^{2} / min$

Hence, the area of the rectangle is increasing at the rate of $2 cm^{2} / min$.

8. A balloon, which always remains spherical on inflation, is being inflated by pumping in 900 cubic centimetres of gas per second. Find the rate at which the radius of the balloon increases when the radius is $15 cm$.

Solution

The volume of a sphere $(V)$ with radius $(r)$ is given by,

$V=\frac{4}{3} \pi r^{3}$

$\therefore$ Rate of change of volume $(V)$ with respect to time $(t)$ is given by,

$\frac{d V}{d t}=\frac{d V}{d r} \cdot \frac{d r}{d t} _{\text{[By chain rule] }}$

$=\frac{d}{d r}(\frac{4}{3} \pi r^{3}) \cdot \frac{d r}{d t}$

$=4 \pi r^{2} \cdot \frac{d r}{d t}$

It is given that $\frac{d V}{d t}=900 cm^{3} / s$.

$\therefore 900=4 \pi r^{2} \cdot \frac{d r}{d t}$

$\Rightarrow \frac{d r}{d t}=\frac{900}{4 \pi r^{2}}=\frac{225}{\pi r^{2}}$

Therefore, when radius $=15 cm$,

$\frac{d r}{d t}=\frac{225}{\pi(15)^{2}}=\frac{1}{\pi}$

Hence, the rate at which the radius of the balloon increases when the radius is $15 cm$

$1 cm / s$.

is $\pi$

9. A balloon, which always remains spherical has a variable radius. Find the rate at which its volume is increasing with the radius when the later is $10 cm$.

Solution

The volume of a sphere $(V)$ with radius $(r)$ is given by $V=\frac{4}{3} \pi r^{3}$.

Rate of change of volume $(V)$ with respect to its radius $(r)$ is given by,

$\frac{d V}{d r}=\frac{d}{d r}(\frac{4}{3} \pi r^{3})=\frac{4}{3} \pi(3 r^{2})=4 \pi r^{2}$

Therefore, when radius $=10 cm$,

$\frac{d V}{d r}=4 \pi(10)^{2}=400 \pi$

Hence, the volume of the balloon is increasing at the rate of $400 cm^{3} / s$.

10. A ladder $5 m$ long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of $2 cm / s$. How fast is its height on the wall decreasing when the foot of the ladder is $4 m$ away from the wall?

Solution

Let $y m$ be the height of the wall at which the ladder touches. Also, let the foot of the ladder be $x$ maway from the wall.

Then, by Pythagoras theorem, we have:

$x^{2}+y^{2}=25$ [Length of the ladder $=5 m$ ]

$\Rightarrow y=\sqrt{25-x^{2}}$

Then, the rate of change of height $(y)$ with respect to time $(t)$ is given by,

$\frac{d y}{d t}=\frac{-x}{\sqrt{25-x^{2}}} \cdot \frac{d x}{d t}$

It is given that $\frac{d x}{d t}=2 cm / s$. $\therefore \frac{d y}{d t}=\frac{-2 x}{\sqrt{25-x^{2}}}$

Now, when $x=4 m$, we have:

$\frac{d y}{d t}=\frac{-2 \times 4}{\sqrt{25-4^{2}}}=-\frac{8}{3}$

Hence, the height of the ladder on the wall is decreasing at the rate of $\frac{8}{3} cm / s$.

11. A particle moves along the curve $6 y=x^{3}+2$. Find the points on the curve at which the $y$-coordinate is changing 8 times as fast as the $x$-coordinate.

Solution

The equation of the curve is given as:

$6 y=x^{3}+2$

The rate of change of the position of the particle with respect to time $(t)$ is given by,

$6 \frac{d y}{d t}=3 x^{2} \frac{d x}{d t}+0$

$\Rightarrow 2 \frac{d y}{d t}=x^{2} \frac{d x}{d t}$

When the $y$-coordinate of the particle changes 8 times as fast as the

$x$-coordinate i.e., $(\frac{d y}{d t}=8 \frac{d x}{d t})$, we have:

$2(8 \frac{d x}{d t})=x^{2} \frac{d x}{d t}$

$\Rightarrow 16 \frac{d x}{d t}=x^{2} \frac{d x}{d t}$

$\Rightarrow(x^{2}-16) \frac{d x}{d t}=0$

$\Rightarrow x^{2}=16$

$\Rightarrow x= \pm 4$

When $x=4, y=\frac{4^{3}+2}{6}=\frac{66}{6}=11$.

When $x=-4, y=\frac{(-4)^{3}+2}{6}=-\frac{62}{6}=-\frac{31}{3}$.

Hence, the points required on the curve are $(4,11)$ and $(-4, \frac{-31}{3})$.

12. The radius of an air bubble is increasing at the rate of $\frac{1}{2} cm / s$. At what rate is the volume of the bubble increasing when the radius is $1 cm$ ?

Solution

The air bubble is in the shape of a sphere.

Now, the volume of an air bubble $(V)$ with radius $(r)$ is given by,

$V=\frac{4}{3} \pi r^{3}$

The rate of change of volume $(V)$ with respect to time $(t)$ is given by,

$ \begin{matrix} \frac{d V}{d t} & =\frac{4}{3} \pi \frac{d}{d r}(r^{3}) \cdot \frac{d r}{d t} & \text{ [By chain rule] } \\ & =\frac{4}{3} \pi(3 r^{2}) \frac{d r}{d t} & \\ & =4 \pi r^{2} \frac{d r}{d t} & \end{matrix} $

It is given that $\frac{d r}{d t}=\frac{1}{2} cm / s$.

Therefore, when $r=1 cm$,

$\frac{d V}{d t}=4 \pi(1)^{2}(\frac{1}{2})=2 \pi cm^{3} / s$

Hence, the rate at which the volume of the bubble increases is $2 \pi cm^{3} / s$.

13. A balloon, which always remains spherical, has a variable diameter $\frac{3}{2}(2 x+1)$. Find the rate of change of its volume with respect to $x$.

Solution

The volume of a sphere $(V)$ with radius $(r)$ is given by,

$V=\frac{4}{3} \pi r^{3}$

It is given that:

Diameter $=\frac{3}{2}(2 x+1)$

$\Rightarrow r=\frac{3}{4}(2 x+1)$

$\therefore V=\frac{4}{3} \pi(\frac{3}{4})^{3}(2 x+1)^{3}=\frac{9}{16} \pi(2 x+1)^{3}$

Hence, the rate of change of volume with respect to $x$ is as

$ \frac{d V}{d x}=\frac{9}{16} \pi \frac{d}{d x}(2 x+1)^{3}=\frac{9}{16} \pi \times 3(2 x+1)^{2} \times 2=\frac{27}{8} \pi(2 x+1)^{2} . $

14. Sand is pouring from a pipe at the rate of $12 cm^{3} / s$. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is $4 cm$ ?

Solution

The volume of a cone $(V)$ with radius $(r)$ and height $(h)$ is given by,

$V=\frac{1}{3} \pi r^{2} h$

It is given that,

$h=\frac{1}{6} r \Rightarrow r=6 h$

$\therefore V=\frac{1}{3} \pi(6 h)^{2} h=12 \pi h^{3}$

The rate of change of volume with respect to time $(t)$ is given by,

$\frac{d V}{d t}=12 \pi \frac{d}{d h}(h^{3}) \cdot \frac{d h}{d t}$ [By chain rule]

$=12 \pi(3 h^{2}) \frac{d h}{d t}$

$=36 \pi h^{2} \frac{d h}{d t}$

It is also given that $\frac{d V}{d t}=12 cm^{3} / s$.

Therefore, when $h=4 cm$, we have:

$ \begin{aligned} & 12=36 \pi(4)^{2} \frac{d h}{d t} \\ & \Rightarrow \frac{d h}{d t}=\frac{12}{36 \pi(16)}=\frac{1}{48 \pi} \end{aligned} $

Hence, when the height of the sand cone is $4 cm$, its height is increasing at the rate

of $\frac{1}{48 \pi} cm / s$.

15. The total cost $C(x)$ in Rupees associated with the production of $x$ units of an item is given by

$\quad\quad$$ C(x)=0.007 x^{3}-0.003 x^{2}+15 x+4000 . $

Find the marginal cost when 17 units are produced.

Solution

Marginal cost is the rate of change of total cost with respect to output.

$\therefore$ Marginal cost (MC) $=\frac{d C}{d x}=0.007(3 x^{2})-0.003(2 x)+15$

$=0.021 x^{2}-0.006 x+15$

When $x=17, M C=0.021(17^{2})-0.006(17)+15$ $=0.021(289)-0.006(17)+15$

$=6.069-0.102+15$

$=20.967$

Hence, when 17 units are produced, the marginal cost is Rs. 20.967.

16. The total revenue in Rupees received from the sale of $x$ units of a product is given by

$\quad\quad$$ R(x)=13 x^{2}+26 x+15 . $

Find the marginal revenue when $x=7$.

Solution

Marginal revenue is the rate of change of total revenue with respect to the number of units sold.

$\therefore$ Marginal Revenue (MR) $=\frac{d R}{d x}=13(2 x)+26=26 x+26$

When $x=7$,

$M R=26(7)+26=182+26=208$

Hence, the required marginal revenue is Rs 208.

Choose the correct answer for questions 17 and 18.

17. The rate of change of the area of a circle with respect to its radius $r$ at $r=6 cm$ is

(A) $10 \pi$

(B) $12 \pi$

(C) $8 \pi$

(D) $11 \pi$

Solution

The area of a circle ( $A$ ) with radius $(r)$ is given by,

$A=\pi r^{2}$

Therefore, the rate of change of the area with respect to its radius $r$ is

$\frac{d A}{d r}=\frac{d}{d r}(\pi r^{2})=2 \pi r$. $\therefore$ When $r=6 cm$,

$\frac{d A}{d r}=2 \pi \times 6=12 \pi cm^{2} / s$

Hence, the required rate of change of the area of a circle is $12 \pi cm^{2} / s$.

The correct answer is $B$.

18. The total revenue in Rupees received from the sale of $x$ units of a product is given by

$R(x)=3 x^{2}+36 x+5$. The marginal revenue, when $x=15$ is

(A) 116

(B) 96

(C) 90

(D) 126

Solution

Marginal revenue is the rate of change of total revenue with respect to the number of units sold.

$\therefore$ Marginal Revenue (MR) $=\frac{d R}{d x}=3(2 x)+36=6 x+36$

$\therefore$ When $x=15$,

$M R=6(15)+36=90+36=126$

Hence, the required marginal revenue is Rs 126 .

The correct answer is D.

6.3 Increasing and Decreasing Functions

In this section, we will use differentiation to find out whether a function is increasing or decreasing or none.

Consider the function $f$ given by $f(x)=x^{2}, x \in \mathbf{R}$. The graph of this function is a parabola as given in Fig 6.1.

Values left to origin

x	$ f(x)=x^2 $
-2	4
$ -\frac{3}{2} $	$ \frac{9}{4} $
-1	1
$ -\frac{1}{2} $	$ \frac{4}{4} $
0	0

as we move from left to right, the height of the graph decreases

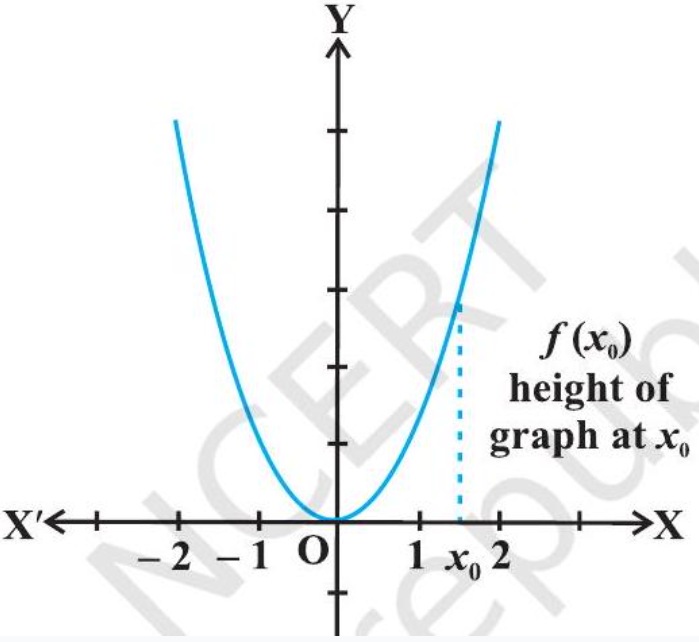
as we move from left to right, the height of the graph increases

Values right to origin

x	$ f(x)=x^2 $
0	0
$ \frac{1}{4} $	$ \frac{1}{4} $
1	1
$ \frac{3}{2} $	$ \frac{9}{4} $
2	4

Fig 6.1

First consider the graph (Fig 6.1) to the right of the origin. Observe that as we move from left to right along the graph, the height of the graph continuously increases. For this reason, the function is said to be increasing for the real numbers $x>0$.

Now consider the graph to the left of the origin and observe here that as we move from left to right along the graph, the height of the graph continuously decreases. Consequently, the function is said to be decreasing for the real numbers $x<0$.

We shall now give the following analytical definitions for a function which is increasing or decreasing on an interval.

Definition 1 Let I be an interval contained in the domain of a real valued function $f$. Then $f$ is said to be

(i) increasing on I if $x_1<x_2$ in $I \Rightarrow f(x_1)<f(x_2)$ for all $x_1, x_2 \in I$.

(ii) decreasing on $I$, if $x_1, x_2$ in $I \Rightarrow f(x_1)<f(x_2)$ for all $x_1, x_2 \in I$.

(iii) constant on $I$, if $f(x)=c$ for all $x \in I$, where $c$ is a constant. (iv) decreasing on I if $x_1<x_2$ in $I \Rightarrow f(x_1) \geq f(x_2)$ for all $x_1, x_2 \in I$.

(v) strictly decreasing on I if $x_1<x_2$ in $I \Rightarrow f(x_1)>f(x_2)$ for all $x_1, x_2 \in I$.

For graphical representation of such functions see Fig 6.2.

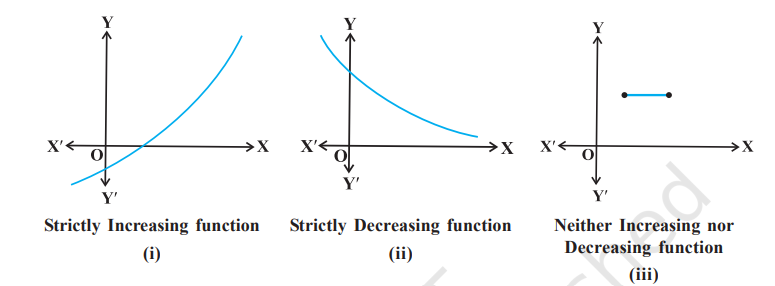
Fig 6.2

We shall now define when a function is increasing or decreasing at a point.

Definition 2 Let $x_0$ be a point in the domain of definition of a real valued function $f$. Then $f$ is said to be increasing, decreasing at $x_0$ if there exists an open interval I containing $x_0$ such that $f$ is increasing, decreasing, respectively, in I.

Let us clarify this definition for the case of increasing function.

Example 7 Show that the function given by $f(x)=7 x-3$ is increasing on $\mathbf{R}$.

Solution Let $x_1$ and $x_2$ be any two numbers in $\mathbf{R}$. Then

$ x_1<x_2 \Rightarrow 7 x_1<7 x_2 \Rightarrow 7 x_1-3<7 x_2-3 \Rightarrow f(x_1)<f(x_2) $

Thus, by Definition 1, it follows that $f$ is strictly increasing on $\mathbf{R}$.

We shall now give the first derivative test for increasing and decreasing functions. The proof of this test requires the Mean Value Theorem studied in Chapter 5.

Theorem 1 Let $f$ be continuous on $[a, b]$ and differentiable on the open interval $(a, b)$. Then

(a) $f$ is increasing in $[a, b]$ if $f^{\prime}(x)>0$ for each $x \in(a, b)$

(b) $f$ is decreasing in $[a, b]$ if $f^{\prime}(x)<0$ for each $x \in(a, b)$

(c) $f$ is a constant function in $[a, b]$ if $f^{\prime}(x)=0$ for each $x \in(a, b)$

Proof (a) Let $x_1, x_2 \in[a, b]$ be such that $x_1<x_2$.

Then, by Mean Value Theorem (Theorem 8 in Chapter 5), there exists a point $c$ between $x_1$ and $x_2$ such that

i.e.

$ f(x_2)-f(x_1)=f^{\prime}(c)(x_2-x_1) $

i.e.

$ f(x_2)-f(x_1)>0 \quad(\text{ as } f^{\prime}(c)>0 \text{ (given) }) $

Thus, we have

$ f(x_2)>f(x_1) $

$ x_1<x_2 \quad f(x_1) \quad f(x_2), \text{ for all } x_1, x_2 \quad[a, b] $

Hence, $f$ is an increasing function in $[a, b]$.

The proofs of part (b) and (c) are similar. It is left as an exercise to the reader.

Remarks

There is a more generalised theorem, which states that if $f \phi(x)>0$ for $x$ in an interval excluding the end points and $f$ is continuous in the interval, then $f$ is increasing. Similarly, if $f \phi(x)<0$ for $x$ in an interval excluding the end points and $f$ is continuous in the interval, then $f$ is decreasing.

Example 8 Show that the function $f$ given by

is increasing on $\mathbf{R}$.

$ f(x)=x^{3}-3 x^{2}+4 x, x \in \mathbf{R} $

Solution Note that

$ \begin{aligned} f^{\prime}(x) & =3 x^{2}-6 x+4 \\ & =3(x^{2}-2 x+1)+1 \\ & =3(x-1)^{2}+1>0, \text{ in every interval of } \mathbf{R} \end{aligned} $

Therefore, the function $f$ is increasing on $\mathbf{R}$.

Example 9 Prove that the function given by $f(x)=\cos x$ is

(a) decreasing in $(0, \pi)$

(b) increasing in $(\pi, 2 \pi)$, and

(c) neither increasing nor decreasing in $(0,2 \pi)$.

Solution Note that $f^{\prime}(x)=-\sin x$

(a) Since for each $x \in(0, \pi), \sin x>0$, we have $f^{\prime}(x)<0$ and so $f$ is decreasing in $(0, \pi)$.

(b) Since for each $x \in(\pi, 2 \pi)$, $\sin x<0$, we have $f^{\prime}(x)>0$ and so $f$ is increasing in $(\pi, 2 \pi)$.

(c) Clearly by (a) and (b) above, $f$ is neither increasing nor decreasing in $(0,2 \pi)$.

Example 10 Find the intervals in which the function $f$ given by $f(x)=x^{2}-4 x+6$ is (a) increasing (b) decreasing

Solution We have

or

$ \begin{aligned} & f(x)=x^{2}-4 x+6 \\ & f^{\prime}(x)=2 x-4 \end{aligned} $

Fig 6.3

Therefore, $f^{\prime}(x)=0$ gives $x=2$. Now the point $x=2$ divides the real line into two disjoint intervals namely, $(-\infty, 2)$ and $(2, \infty)$ (Fig 6.3). In the interval $(-\infty, 2), f^{\prime}(x)=2 x$ $-4<0$.

Therefore, $f$ is decreasing in this interval. Also, in the interval $(2, \infty), f^{\prime}(x)>0$ and so the function $f$ is increasing in this interval.

Example 11 Find the intervals in which the function $f$ given by $f(x)=4 x^{3}-6 x^{2}-72 x$ +30 is (a) increasing (b) decreasing.

Solution We have

$ \text{ or } \quad \begin{aligned} f(x) & =4 x^{3}-6 x^{2}-72 x+30 \\ f^{\prime}(x) & =12 x^{2}-12 x-72 \\ & =12(x^{2}-x-6) \\ & =12(x-3)(x+2) \end{aligned} $

Therefore, $f^{\prime}(x)=0$ gives $x=-2,3$. The points $x=-2$ and $x=3$ divides the real line into three disjoint intervals, namely, $(-\infty,-2),(-2,3)$

Fig 6.4 and $(3, \infty)$.

In the intervals $(-\infty,-2)$ and $(3, \infty), f^{\prime}(x)$ is positive while in the interval $(-2,3)$, $f^{\prime}(x)$ is negative. Consequently, the function $f$ is increasing in the intervals $(-\infty,-2)$ and $(3, \infty)$ while the function is decreasing in the interval $(-2,3)$. However, $f$ is neither increasing nor decreasing in $\mathbf{R}$.

Interval	Sign of $ f’(x) $	Nature of function f
$ (\infty, -2) $	(-)(-)>0	f is increasing
(-2,3)	(-)(+)<0	f is decreasing
$ (3,\infty)$	(+)(+)>0	f is increasing

Example 12 Find intervals in which the function given by $f(x)=\sin 3 x, x \in 0, \frac{\pi}{2}$ is (a) increasing (b) decreasing.

Solution We have

$f(x) =\sin 3 x $

or $\quad f(x) =3 \cos 3 x$

Therefore, $f^{\prime}(x)=0$ gives $\cos 3 x=0$ which in turn gives $3 x=\frac{\pi}{2}, \frac{3 \pi}{2}$ (as $x \in 0, \frac{\pi}{2}$ implies $3 x \in[0, \frac{3 \pi}{2}]$ ). So $x=\frac{\pi}{6}$ and $\frac{\pi}{2}$. The point $x=\frac{\pi}{6}$ divides the interval $0, \frac{\pi}{2}$ into two disjoint intervals $[0, \frac{\pi}{6})$ and $\frac{\pi}{6}, \frac{\pi}{2}$.

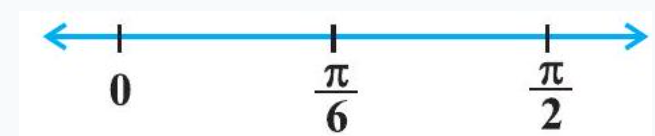
Fig 6.5

Now, $f^{\prime}(x)>0$ for all $x \in[0, \frac{\pi}{6})$ as $0 \leq x<\frac{\pi}{6} \Rightarrow 0 \leq 3 x<\frac{\pi}{2}$ and $f^{\prime}(x)<0$ for all $x \in(\frac{\pi}{6}, \frac{\pi}{2})$ as $\frac{\pi}{6}<x<\frac{\pi}{2} \Rightarrow \frac{\pi}{2}<3 x<\frac{3 \pi}{2}$.

Therefore, $f$ is increasing in $[0, \frac{\pi}{6})$ and decreasing in $(\frac{\pi}{6}, \frac{\pi}{2})$.

Also, the given function is continuous at $x=0$ and $x=\frac{\pi}{6}$. Therefore, by Theorem 1 , $f$ is increasing on $ [0, \frac{\pi}{6}]$ and decreasing on $[\frac{\pi}{6}, \frac{\pi}{2}]$.

Example 13 Find the intervals in which the function $f$ given by

$ f(x)=\sin x+\cos x, 0 \leq x \leq 2 \pi $

is increasing or decreasing.

Solution We have

$ \begin{aligned} f(x) & =\sin x+\cos x, \\ \text{ or } \quad f^{\prime}(x) & =\cos x-\sin x \end{aligned} $

Now $f^{\prime}(x)=0$ gives $\sin x=\cos x$ which gives that $x=\frac{\pi}{4}, \frac{5 \pi}{4}$ as $0 \leq x \leq 2 \pi$

The points $x=\frac{\pi}{4}$ and $x=\frac{5 \pi}{4}$ divide the interval $[0,2 \pi]$ into three disjoint intervals,

namely, $[0, \frac{\pi}{4}), \frac{\pi}{4}, \frac{5 \pi}{4}$ and $(\frac{5 \pi}{4}, 2 \pi]$.

Fig 6.6

Note that $f^{\prime}(x)>0$ if $x \in[0, \frac{\pi}{4}) \cup(\frac{5 \pi}{4}, 2 \pi]$

or $\quad f$ is increasing in the intervals $[0, \frac{\pi}{4})$ and $(\frac{5 \pi}{4}, 2 \pi]$

Also $\quad f^{\prime}(x)<0$ if $x \in \frac{\pi}{4}, \frac{5 \pi}{4}$

or $\quad f$ is decreasing in $\frac{\pi}{4}, \frac{5 \pi}{4}$

Interval	Sign of f’(x)	Nature of function
[$ 0, \frac{\pi}{4} $]	>0	f is increasing
$ (\frac{\pi}{4}, \frac{5\pi}{4}) $	<0	f is decreasing
$ (\frac{5 \pi}{4},2\pi $ $	>0	f is increasing

EXERCISE 6.2

1. Show that the function given by $f(x)=3 x+17$ is increasing on $\mathbf{R}$.

Solution

Let ${ }^{x_1}$ and $x_2$ be any two numbers in $\mathbf{R}$.

Then, we have:

$x_1<x_2 \Rightarrow 3 x_1<3 x_2 \Rightarrow 3 x_1+17<3 x_2+17 \Rightarrow f(x_1)<f(x_2)$

Hence, $f$ is strictly increasing on $\mathbf{R}$.

Alternate method:

$f(x)=3>0$, in every interval of $\mathbf{R}$.

Thus, the function is strictly increasing on $\mathbf{R}$.

2. Show that the function given by $f(x)=e^{2 x}$ is increasing on $\mathbf{R}$.

Solution

Let ${ }^{x_1}$ and $x_2$ be any two numbers in $\mathbf{R}$.

Then, we have:

$x_1<x_2 \Rightarrow 2 x_1<2 x_2 \Rightarrow e^{2 x_1}<e^{2 x_2} \Rightarrow f(x_1)<f(x_2)$

Hence, $f$ is strictly increasing on $\mathbf{R}$.

3. Show that the function given by $f(x)=\sin x$ is

(a) increasing in $(0, \frac{\pi}{2})$

(b) decreasing in $(\frac{\pi}{2}, \pi)$

(c) neither increasing nor decreasing in $(0, \pi)$

Solution

The given function is $f(x)=\sin x$.

$\therefore f^{\prime}(x)=\cos x$ (a) Since for each $x \in(0, \frac{\pi}{2}), \cos x>0$, we have $f^{\prime}(x)>0$.

Hence, $f$ is strictly increasing in $(0, \frac{\pi}{2})$.

(b) Since for each $x \in(\frac{\pi}{2}, \pi), \cos x<0$, we have $f^{\prime}(x)<0$.

Hence, $f$ is strictly decreasing in $(\frac{\pi}{2}, \pi)$.

(c) From the results obtained in (a) and (b), it is clear that $f$ is neither increasing nor decreasing in $(0, \pi)$.

4. Find the intervals in which the function $f$ given by $f(x)=2 x^{2}-3 x$ is

(a) increasing

(b) decreasing

Solution

The given function is $f(x)=2 x^{2}-3 x$.

$f^{\prime}(x)=4 x-3$

$\therefore f^{\prime}(x)=0 \Rightarrow x=\frac{3}{4}$

Now, the point $\frac{3}{4}$ divides the real line into two disjoint intervals i.e., $(-\infty, \frac{3}{4})$ and $(\frac{3}{4}, \infty)$.

In interval $(-\infty, \frac{3}{4}), f^{\prime}(x)=4 x-3<0$.

Hence, the given function $(f)$ is strictly decreasing in interval $(-\infty, \frac{3}{4})$.

In interval $(\frac{3}{4}, \infty), f^{\prime}(x)=4 x-3>0$.

Hence, the given function $(f)$ is strictly increasing in interval $(\frac{3}{4}, \infty)$.

5. Find the intervals in which the function $f$ given by $f(x)=2 x^{3}-3 x^{2}-36 x+7$ is

(a) increasing

(b) decreasing

Solution

The given function is $f(x)=2 x^{3}-3 x^{2}-36 x+7$.

$f^{\prime}(x)=6 x^{2}-6 x-36=6(x^{2}-x-6)=6(x+2)(x-3)$

$\therefore f^{\prime}(x)=0 \Rightarrow x=-2,3$

The points $x=-2$ and $x=3$ divide the real line into three disjoint intervals i.e., $(-\infty,-2),(-2,3)$, and $(3, \infty)$.

In intervals $(-\infty,-2)$ and $(3, \infty), f^{\prime}(x)$ is positive while in interval

$(-2,3), f^{\prime}(x)$ is negative.

Hence, the given function $(f)$ is strictly increasing in intervals

$(-\infty,-2)$ and $(3, \infty)$, while function $(f)$ is strictly decreasing in interval

$(-2,3)$.

6. Find the intervals in which the following functions are strictly increasing or decreasing:

(a) $x^{2}+2 x-5$

(b) $10-6 x-2 x^{2}$

(c) $-2 x^{3}-9 x^{2}-12 x+1$

(d) $6-9 x-x^{2}$

(e) $(x+1)^{3}(x-3)^{3}$

Solution

(a) We have,

$f(x)=x^{2}+2 x-5$

$\therefore f^{\prime}(x)=2 x+2$

Now,

$f^{\prime}(x)=0 \Rightarrow x=-1$

Point $x=-1$ divides the real line into two disjoint intervals i.e., $(-\infty,-1)$ and $(-1, \infty)$.

In interval $(-\infty,-1), f^{\prime}(x)=2 x+2<0$.

$\therefore f$ is strictly decreasing in interval $(-\infty,-1)$.

Thus, $f$ is strictly decreasing for $x<-1$.

In interval $(-1, \infty), f^{\prime}(x)=2 x+2>0$.

$\therefore f$ is strictly increasing in interval $(-1, \infty)$.

Thus, $f$ is strictly increasing for $x>-1$.

(b) We have,

$f(x)=10-6 x-2 x^{2}$

$\therefore f^{\prime}(x)=-6-4 x$

Now,

$f^{\prime}(x)=0 \Rightarrow x=-\frac{3}{2}$

The point $x=-\frac{3}{2}$ divides the real line into two disjoint intervals

i.e., $(-\infty,-\frac{3}{2})$ and $(-\frac{3}{2}, \infty)$.

In interval $(-\infty,-\frac{3}{2})$ i.e., when $x<-\frac{3}{2}, f^{\prime}(x)=-6-4 x<0$.

$\therefore f$ is strictly increasing for $x<-\frac{3}{2}$.

In interval $(-\frac{3}{2}, \infty)$ i.e., when $x>-\frac{3}{2}, f^{\prime}(x)=-6-4 x<0$.

$\therefore f$ is strictly decreasing for $x>-\frac{3}{2}$.

(c) We have,

$f(x)=-2 x^{3}-9 x^{2}-12 x+1$

$\therefore f^{\prime}(x)=-6 x^{2}-18 x-12=-6(x^{2}+3 x+2)=-6(x+1)(x+2)$

Now,

$f^{\prime}(x)=0 \Rightarrow x=-1$ and $x=-2$

Points $x=-1$ and $x=-2$ divide the real line into three disjoint intervals

i.e., $(-\infty,-2),(-2,-1)$, and $(-1, \infty)$.

In intervals $(-\infty,-2)$ and $(-1, \infty)$ i.e., when $x<-2$ and $x>-1$,

$f^{\prime}(x)=-6(x+1)(x+2)<0$. $\therefore f$ is strictly decreasing for $x<-2$ and $x>-1$.

Now, in interval $(-2,-1)$ i.e., when $-2<x<-1, f^{\prime}(x)=-6(x+1)(x+2)>0$.

$\therefore f$ is strictly increasing for $-2<x<-1$.

(d) We have,

$ \begin{aligned} & f(x)=6-9 x-x^{2} \\ & \therefore f^{\prime}(x)=-9-2 x \end{aligned} $

Now, $f^{\prime}$

$(x)=0$ gives $x=-\frac{9}{2}$

The point $x=-\frac{9}{2}$ divides the real line into two disjoint intervals i.e.,

$(-\infty,-\frac{9}{2})$ and $(-\frac{9}{2}, \infty)$.

In interval $(-\infty,-\frac{9}{2})$ i.e., for $x<-\frac{9}{2}, f^{\prime}(x)=-9-2 x>0$.

$\therefore f$ is strictly increasing for $x<-\frac{9}{2}$.

In interval $(-\frac{9}{2}, \infty)$ i.e., for $x>-\frac{9}{2}, f^{\prime}(x)=-9-2 x<0$. $\therefore f$ is strictly decreasing for $x>-\frac{9}{2}$.

(e) We have,

$ \begin{aligned} f(x)= & (x+1)^{3}(x-3)^{3} \\ f^{\prime}(x) & =3(x+1)^{2}(x-3)^{3}+3(x-3)^{2}(x+1)^{3} \\ & =3(x+1)^{2}(x-3)^{2}[x-3+x+1] \\ & =3(x+1)^{2}(x-3)^{2}(2 x-2) \\ & =6(x+1)^{2}(x-3)^{2}(x-1) \end{aligned} $

Now,

$f^{\prime}(x)=0 \Rightarrow x=-1,3,1$

The points $x=-1, x=1$, and $x=3$ divide the real line into four disjoint intervals

i.e., $(-\infty,-1),(-1,1),(1,3)$, and $(3, \infty)$.

In intervals $(-\infty,-1)$ and $(-1,1), f^{\prime}(x)=6(x+1)^{2}(x-3)^{2}(x-1)<0$.

$\therefore f$ is strictly decreasing in intervals $(-\infty,-1)$ and $(-1,1)$.

In intervals $(1,3)$ and $(3, \infty), f^{\prime}(x)=6(x+1)^{2}(x-3)^{2}(x-1)>0$.

$\therefore f$ is strictly increasing in intervals $(1,3)$ and $(3, \infty)$.

7. Show that $y=\log (1+x)-\frac{2 x}{2+x}, x>-1$, is an increasing function of $x$ throughout its domain.

Solution

We have,

$ \begin{aligned} & y=\log (1+x)-\frac{2 x}{2+x} \\ & \therefore \frac{d y}{d x}=\frac{1}{1+x}-\frac{(2+x)(2)-2 x(1)}{(2+x)^{2}}=\frac{1}{1+x}-\frac{4}{(2+x)^{2}}=\frac{x^{2}}{(2+x)^{2}} \end{aligned} $

Now, $\frac{d y}{d x}=0$

$\Rightarrow \frac{x^{2}}{(2+x)^{2}}=0$

$\Rightarrow x^{2}=0 \quad[(2+x) \neq 0$ as $x>-1]$

$\Rightarrow x=0$

Since $x>-1$, point $x=0$ divides the domain $(-1, \infty)$ in two disjoint intervals i.e., $-1<$ $x<0$ and $x>0$.

When $-1<x<0$, we have:

$x<0 \Rightarrow x^{2}>0$

$x>-1 \Rightarrow(2+x)>0 \Rightarrow(2+x)^{2}>0$

$\therefore y^{\prime}=\frac{x^{2}}{(2+x)^{2}}>0$

Also, when $x>0$ :

$x>0 \Rightarrow x^{2}>0,(2+x)^{2}>0$

$\therefore y^{\prime}=\frac{x^{2}}{(2+x)^{2}}>0$

Hence, function $f$ is increasing throughout this domain.

8. Find the values of $x$ for which $y=[x(x-2)]^{2}$ is an increasing function.

Solution

We have,

$y=[x(x-2)]^{2}=[x^{2}-2 x]^{2}$

$\therefore \frac{d y}{d x}=y^{\prime}=2(x^{2}-2 x)(2 x-2)=4 x(x-2)(x-1)$

$\therefore \frac{d y}{d x}=0 \Rightarrow x=0, x=2, x=1$.

The points $x=0, x=1$, and $x=2$ divide the real line into four disjoint intervals i.e., $(-\infty, 0),(0,1)(1,2)$, and $(2, \infty)$.

In intervals $(-\infty, 0)$ and $(1,2), \frac{d y}{d x}<0$.

$\therefore y$ is strictly decreasing in intervals $(-\infty, 0)$ and $(1,2)$.

However, in intervals $(0,1)$ and $(2, \infty), \frac{d y}{d x}>0$.

$\therefore y$ is strictly increasing in intervals $(0,1)$ and $(2, \infty)$.

$\therefore y$ is strictly increasing for $0<x<1$ and $x>2$.

9. Prove that $y=\frac{4 \sin \theta}{(2+\cos \theta)}-\theta$ is an increasing function of $\theta$ in $0, \frac{\pi}{2}$.

Solution

We have,

$ \begin{aligned} & y=\frac{4 \sin \theta}{(2+\cos \theta)}-\theta \\ & \begin{aligned} \therefore \frac{d y}{d x} & =\frac{(2+\cos \theta)(4 \cos \theta)-4 \sin \theta(-\sin \theta)}{(2+\cos \theta)^{2}}-1 \\ \quad & \frac{8 \cos \theta+4 \cos ^{2} \theta+4 \sin ^{2} \theta}{(2+\cos \theta)^{2}}-1 \\ \quad & \frac{8 \cos \theta+4}{(2+\cos \theta)^{2}}-1 \end{aligned} \end{aligned} $

Now, $\frac{d y}{d x}=0$.

$\Rightarrow \frac{8 \cos \theta+4}{(2+\cos \theta)^{2}}=1$

$\Rightarrow 8 \cos \theta+4=4+\cos ^{2} \theta+4 \cos \theta$

$\Rightarrow \cos ^{2} \theta-4 \cos \theta=0$

$\Rightarrow \cos \theta(\cos \theta-4)=0$

$\Rightarrow \cos \theta=0$ or $\cos \theta=4$

Since $\cos \theta \neq 4, \cos \theta=0$.

$\cos \theta=0 \Rightarrow \theta=\frac{\pi}{2}$

Now,

$\frac{d y}{d x}=\frac{8 \cos \theta+4-(4+\cos ^{2} \theta+4 \cos \theta)}{(2+\cos \theta)^{2}}=\frac{4 \cos \theta-\cos ^{2} \theta}{(2+\cos \theta)^{2}}=\frac{\cos \theta(4-\cos \theta)}{(2+\cos \theta)^{2}}$

In interval $(0, \frac{\pi}{2})$, we have $\cos \theta>0$. Also, $4>\cos \theta \Rightarrow 4-\cos \theta>0$.

$\therefore \cos \theta(4-\cos \theta)>0$ and also $(2+\cos \theta)^{2}>0$

$\Rightarrow \frac{\cos \theta(4-\cos \theta)}{(2+\cos \theta)^{2}}>0$

$\Rightarrow \frac{d y}{d x}>0$

Therefore, $y$ is strictly increasing in interval $(0, \frac{\pi}{2})$.

Also, the given function is continuous at $x=0$ and $x=\frac{\pi}{2}$.

Hence, $y$ is increasing in interval $[0, \frac{\pi}{2}]$.

10. Prove that the logarithmic function is increasing on $(0, \infty)$.

Solution

The given function is $f(x)=\log x$.

$\therefore f^{\prime}(x)=\frac{1}{x}$

It is clear that for $x>0, f^{\prime}(x)=\frac{1}{x}>0$.

Hence, $f(x)=\log x$ is strictly increasing in interval $(0, \infty)$.

11. Prove that the function $f$ given by $f(x)=x^{2}-x+1$ is neither strictly increasing nor decreasing on $(-1,1)$.

Solution

The given function is $f(x)=x^{2}-x+1$.

$\therefore f^{\prime}(x)=2 x-1$

Now, $f^{\prime}(x)=0 \Rightarrow x=\frac{1}{2}$.

The point $\frac{1}{2}$ divides the interval $(-1,1)$ into two disjoint intervals

i.e., $(-1, \frac{1}{2})$ and $(\frac{1}{2}, 1)$.

Now, in interval $(-1, \frac{1}{2}), f^{\prime}(x)=2 x-1<0$.

Therefore, $f$ is strictly decreasing in interval $(-1, \frac{1}{2})$.

However, in interval $(\frac{1}{2}, 1), f^{\prime}(x)=2 x-1>0$.

Therefore, $f$ is strictly increasing in interval $(\frac{1}{2}, 1)$.

Hence, $f$ is neither strictly increasing nor decreasing in interval $(-1,1)$.

12. Which of the following functions are decreasing on $0, \frac{\pi}{2}$ ?

(A) $\cos x$

(B) $\cos 2 x$

(C) $\cos 3 x$

(D) $\tan x$

Solution

(A) Let $f_1(x)=\cos x$.

$\therefore f_1^{\prime}(x)=-\sin x$

In interval $(0, \frac{\pi}{2}), f_1^{\prime}(x)=-\sin x<0$.

$\therefore f_1(x)=\cos x _{\text{is strictly decreasing in interval }}(0, \frac{\pi}{2})$.

(B) Let $f_2(x)=\cos 2 x$.

$\therefore f_2^{\prime}(x)=-2 \sin 2 x$

Now, $0<x<\frac{\pi}{2} \Rightarrow 0<2 x<\pi \Rightarrow \sin 2 x>0 \Rightarrow-2 \sin 2 x<0$

$\therefore f_2^{\prime}(x)=-2 \sin 2 x<0$ on $(0, \frac{\pi}{2})$

$\therefore f_2(x)=\cos 2 x$ is strictly decreasing in interval $(0, \frac{\pi}{2})$.

(C) Let $f_3(x)=\cos 3 x$.

$\therefore f_3^{\prime}(x)=-3 \sin 3 x$

Now, $f_3^{\prime}(x)=0$.

$\Rightarrow \sin 3 x=0 \Rightarrow 3 x=\pi$, as $x \in(0, \frac{\pi}{2})$

$\Rightarrow x=\frac{\pi}{3}$

The point $x=\frac{\pi}{3}$ divides the interval $(0, \frac{\pi}{2})$ into two disjoint intervals

i.e., $0(0, \frac{\pi}{3})$ and $(\frac{\pi}{3}, \frac{\pi}{2})$.

Now, in interval $(0, \frac{\pi}{3}), f_3(x)=-3 \sin 3 x<0[.$ as $.0<x<\frac{\pi}{3} \Rightarrow 0<3 x<\pi]$.

$\therefore f_3$ is strictly decreasing in interval $(0, \frac{\pi}{3})$.

However, in interval $(\frac{\pi}{3}, \frac{\pi}{2}), f_3(x)=-3 \sin 3 x>0[.$ as $.\frac{\pi}{3}<x<\frac{\pi}{2} \Rightarrow \pi<3 x<\frac{3 \pi}{2}]$. $\therefore f_3$ is strictly increasing in interval $(\frac{\pi}{3}, \frac{\pi}{2})$.

Hence, $f_3$ is neither increasing nor decreasing in interval $(0, \frac{\pi}{2})$.

(D) Let $f_4(x)=\tan x$.

$\therefore f_4^{\prime}(x)=\sec ^{2} x$

In interval $(0, \frac{\pi}{2}), f_4^{\prime}(x)=\sec ^{2} x>0$.

$\therefore f_4$ is strictly increasing in interval $(0, \frac{\pi}{2})$.

Therefore, functions $\cos x$ and $\cos 2 x$ are strictly decreasing in $(0, \frac{\pi}{2})$. Hence, the correct answers are A and B.

13. On which of the following intervals is the function $f$ given by $f(x)=x^{100}+\sin x-1$ decreasing?

(A) $(0,1)$

(B) $\frac{\pi}{2}, \pi$

(C) $0, \frac{\pi}{2}$

(D) None of these

Solution

We have, $f(x)=x^{100}+\sin x-1$

$\therefore f^{\prime}(x)=100 x^{99}+\cos x$

In interval $(0,1), \cos x>0$ and $100 x^{99}>0$.

$\therefore f^{\prime}(x)>0$.

Thus, function $f$ is strictly increasing in interval $(0,1)$.

In interval $(\frac{\pi}{2}, \pi), \cos x<0$ and $100 x^{99}>0$. Also, $100 x^{99}>\cos x$.

$\therefore f^{\prime}(x)>0$ in $(\frac{\pi}{2}, \pi)$.

Thus, function $f$ is strictly increasing in interval $(\frac{\pi}{2}, \pi)$.

In interval $(0, \frac{\pi}{2}), \cos x>0$ and $100 x^{99}>0$.

$\therefore 100 x^{99}+\cos x>0$

$\Rightarrow f^{\prime}(x)>0$ on $(0, \frac{\pi}{2})$

$\therefore f$ is strictly increasing in interval $(0, \frac{\pi}{2})$.

Hence, function $f$ is strictly decreasing in none of the intervals.

The correct answer is D.

14. For what values of $a$ the function $f$ given by $f(x)=x^{2}+a x+1$ is increasing on $[1,2]$ ?

Solution

We have, $f(x)=x^{2}+a x+1$

$\therefore f^{\prime}(x)=2 x+a$

Now, function $f$ will be increasing in $(1,2)$, if $f^{\prime}(x)>0$ in $(1,2)$.

$f^{\prime}(x)>0$

$\Rightarrow 2 x+a>0$

$\Rightarrow 2 x>-a$

$\Rightarrow \quad x>\frac{-a}{2}$

Therefore, we have to find the least value of $a$ such that

$x>\frac{-a}{2}$, when $x \in(1,2)$.

$\Rightarrow x>\frac{-a}{2}($ when $1<x<2)$

Thus, the least value of $a$ for $f$ to be increasing on $(1,2)$ is given by,

$\frac{-a}{2}=1$

$\frac{-a}{2}=1 \Rightarrow a=-2$

Hence, the required value of $a$ is -2 .

15. Let $I$ be any interval disjoint from $[-1,1]$. Prove that the function $f$ given by $f(x)=x+\frac{1}{x}$ is increasing on $I$.

Solution

We have,

$f(x)=x+\frac{1}{x}$

$\therefore f^{\prime}(x)=1-\frac{1}{x^{2}}$

Now,

$f^{\prime}(x)=0 \Rightarrow \frac{1}{x^{2}}=1 \Rightarrow x= \pm 1$

The points $x=1$ and $x=-1$ divide the real line in three disjoint intervals i.e.,

$(-\infty,-1),(-1,1)$, and $(1, \infty)$.

In interval $(-1,1)$, it is observed that:

$-1<x<1$

$\Rightarrow x^{2}<1$

$\Rightarrow 1<\frac{1}{x^{2}}, x \neq 0$

$\Rightarrow 1-\frac{1}{x^{2}}<0, x \neq 0$

$\therefore f^{\prime}(x)=1-\frac{1}{x^{2}}<0$ on $(-1,1) \sim{0}$.

$\therefore f$ is strictly decreasing on $(-1,1) \sim{0}$.

In intervals $(-\infty,-1)$ and $(1, \infty)$, it is observed that: $x<-1$ or $1<x$

$\Rightarrow x^{2}>1$

$\Rightarrow 1>\frac{1}{x^{2}}$

$\Rightarrow 1-\frac{1}{x^{2}}>0$

$\therefore f^{\prime}(x)=1-\frac{1}{x^{2}}>0$ on $(-\infty,-1)$ and $(1, \infty)$.

$\therefore f$ is strictly increasing on $(-\infty, 1)$ and $(1, \infty)$.

Hence, function $f$ is strictly increasing in interval $\mathbf{I}$ disjoint from $(-1,1)$. Hence, the given result is proved.

16. Prove that the function $f$ given by $f(x)=\log \sin x$ is increasing on $0, \frac{\pi}{2}$ and decreasing on $\frac{\pi}{2}, \pi$

Solution

We have,

$f(x)=\log \sin x$

$\therefore f^{\prime}(x)=\frac{1}{\sin x} \cos x=\cot x$

In interval $(0, \frac{\pi}{2}), f^{\prime}(x)=\cot x>0$.

$\therefore f$ is strictly increasing in $(0, \frac{\pi}{2})$.

In interval $(\frac{\pi}{2}, \pi), f^{\prime}(x)=\cot x<0$.

$\therefore f$ is strictly decreasing in $(\frac{\pi}{2}, \pi)$.

17. Prove that the function $f$ given by $f(x)=\log |\cos x|$ is decreasing on $(0, \frac{\pi}{2})$ and increasing on $(\frac{3 \pi}{2}, 2 \pi)$.

Solution

We have,

$f(x)=\log \cos x$

$\therefore f^{\prime}(x)=\frac{1}{\cos x}(-\sin x)=-\tan x$

In interval $(0, \frac{\pi}{2}), \tan x>0 \Rightarrow-\tan x<0$.

$\therefore f^{\prime}(x)<0$ on $(0, \frac{\pi}{2})$

$\therefore f$ is strictly decreasing on $(0, \frac{\pi}{2})$.

In interval $(\frac{\pi}{2}, \pi), \tan x<0 \Rightarrow-\tan x>0$.

$\therefore f^{\prime}(x)>0$ on $(\frac{\pi}{2}, \pi)$ $\therefore f$ is strictly increasing on $(\frac{\pi}{2}, \pi)$.

18. Prove that the function given by $f(x)=x^{3}-3 x^{2}+3 x-100$ is increasing in $\mathbf{R}$.

Solution

We have,

$f(x)=x^{3}-3 x^{2}+3 x-100$

$ \begin{aligned} f^{\prime}(x) & =3 x^{2}-6 x+3 \\ & =3(x^{2}-2 x+1) \\ & =3(x-1)^{2} \end{aligned} $

For any $x \in \mathbf{R},(x-1)^{2}>0$.

Thus, $f^{\prime}(x)$ is always positive in $\mathbf{R}$.

Hence, the given function $(f)$ is increasing in $\mathbf{R}$.

19. The interval in which $y=x^{2} e^{-x}$ is increasing is

(A) $(-\infty, \infty)$

(B) $(-2,0)$

(C) $(2, \infty)$

(D) $(0,2)$

Solution

We have,

$y=x^{2} e^{-x}$ $\therefore \frac{d y}{d x}=2 x e^{-x}-x^{2} e^{-x}=x e^{-x}(2-x)$

Now, $\frac{d y}{d x}=0$.

$\Rightarrow x=0$ and $x=2$

The points $x=0$ and $x=2$ divide the real line into three disjoint intervals

i.e., $(-\infty, 0),(0,2)$, and $(2, \infty)$.

In intervals $(-\infty, 0)$ and $(2, \infty), f^{\prime}(x)<0$ as $e^{-x}$ is always positive.

$\therefore f$ is decreasing on $(-\infty, 0)$ and $(2, \infty)$.

In interval $(0,2), f^{\prime}(x)>0$.

$\therefore f$ is strictly increasing on $(0,2)$.

Hence, $f$ is strictly increasing in interval $(0,2)$.

The correct answer is D.

Maxima and Minima

In this section, we will use the concept of derivatives to calculate the maximum or minimum values of various functions. In fact, we will find the ’turning points’ of the graph of a function and thus find points at which the graph reaches its highest (or lowest) locally. The knowledge of such points is very useful in sketching the graph of a given function. Further, we will also find the absolute maximum and absolute minimum of a function that are necessary for the solution of many applied problems.

Let us consider the following problems that arise in day to day life.

(i) The profit from a grove of orange trees is given by $P(x)=a x+b x^{2}$, where $a, b$ are constants and $x$ is the number of orange trees per acre. How many trees per acre will maximise the profit?

(ii) A ball, thrown into the air from a building 60 metres high, travels along a path given by $h(x)=60+x-\frac{x^{2}}{60}$, where $x$ is the horizontal distance from the building and $h(x)$ is the height of the ball . What is the maximum height the ball will reach?

(iii) An Apache helicopter of enemy is flying along the path given by the curve $f(x)=x^{2}+7$. A soldier, placed at the point $(1,2)$, wants to shoot the helicopter when it is nearest to him. What is the nearest distance?

In each of the above problem, there is something common, i.e., we wish to find out the maximum or minimum values of the given functions. In order to tackle such problems, we first formally define maximum or minimum values of a function, points of local maxima and minima and test for determining such points.

Definition 3 Let $f$ be a function defined on an interval I. Then

(a) $f$ is said to have a maximum value in I, if there exists a point $c$ in I such that $f(c)>f(x)$, for all $x \in I$.

The number $f(c)$ is called the maximum value of $f$ in I and the point $c$ is called a point of maximum value of $f$ in $I$.

(b) $f$ is said to have a minimum value in $I$, if there exists a point $c$ in $I$ such that $f(c)<f(x)$, for all $x \in I$.

The number $f(c)$, in this case, is called the minimum value of $f$ in I and the point $c$, in this case, is called a point of minimum value of $f$ in $I$.

(c) $f$ is said to have an extreme value in $I$ if there exists a point $c$ in I such that $f(c)$ is either a maximum value or a minimum value of $f$ in $I$.

The number $f(c)$, in this case, is called an extreme value of $f$ in $I$ and the point $c$ is called an extreme point.

Remark In Fig 6.7(a), (b) and (c), we have exhibited that graphs of certain particular functions help us to find maximum value and minimum value at a point. Infact, through graphs, we can even find maximum/minimum value of a function at a point at which it is not even differentiable (Example 15 ).

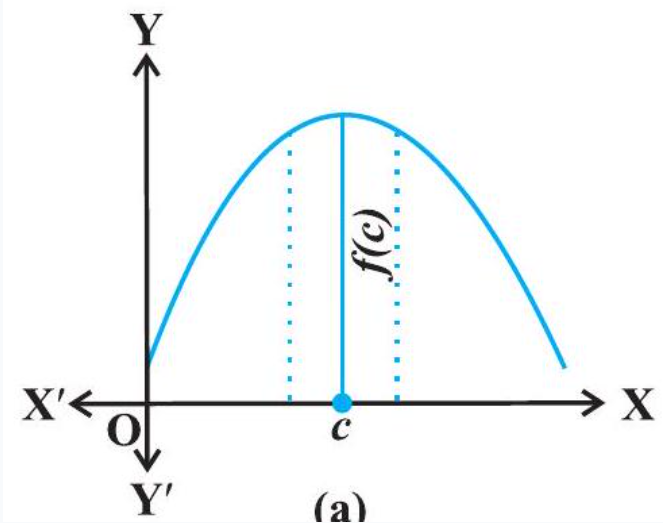
(a)

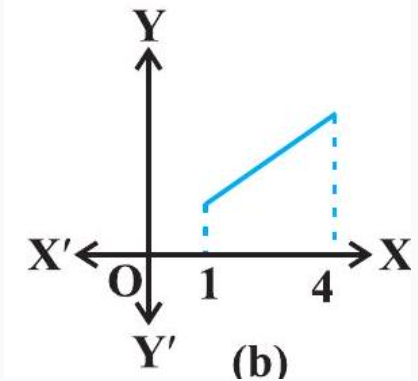(b)

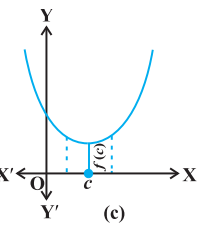
(c)

Fig 6.7

Example 14 Find the maximum and the minimum values, if any, of the function $f$ given by

$ f(x)=x^{2}, x \in \mathbf{R} . $

Solution From the graph of the given function (Fig 6.8), we have $f(x)=0$ if $x=0$. Also

$ f(x) \geq 0 \text{, for all } x \in \mathbf{R} \text{. } $

Therefore, the minimum value of $f$ is 0 and the point of minimum value of $f$ is $x=0$. Further, it may be observed from the graph of the function that $f$ has no maximum value and hence no point of maximum value of $f$ in $\mathbf{R}$.

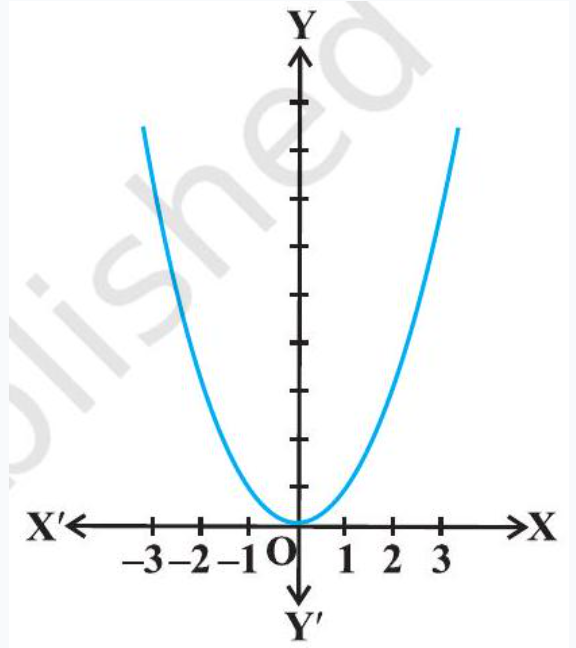
Fig 6.8

Note If we restrict the domain of $f$ to $[-2,1]$ only, then $f$ will have maximum value $(-2)^{2}=4$ at $x=-2$.

Example 15 Find the maximum and minimum values of $f$, if any, of the function given by $f(x)=|x|, x \in \mathbf{R}$.

Solution From the graph of the given function (Fig 6.9), note that

$ f(x) \geq 0 \text{, for all } x \in \mathbf{R} \text{ and } f(x)=0 \text{ if } x=0 \text{. } $

Therefore, the function $f$ has a minimum value 0 and the point of minimum value of $f$ is $x=0$. Also, the graph clearly shows that $f$ has no maximum value in $\mathbf{R}$ and hence no point of maximum value in $\mathbf{R}$.

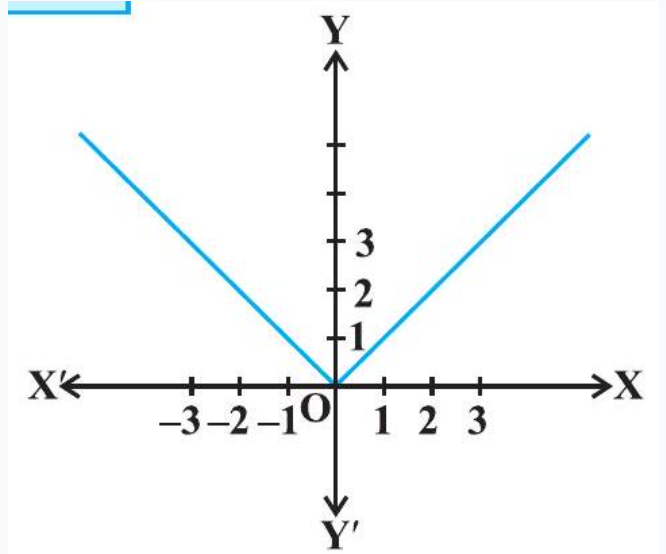
Fig 6.9

Note

(i) If we restrict the domain of $f$ to $[-2,1]$ only, then $f$ will have maximum value $|-2|=2$. (ii) One may note that the function $f$ in Example 27 is not differentiable at $x=0$.

Example 16 Find the maximum and the minimum values, if any, of the function given by

$ f(x)=x, x \in(0,1) . $

Solution The given function is an increasing (strictly) function in the given interval $(0,1)$. From the graph (Fig 6.10) of the function $f$, it seems that, it should have the minimum value at a point closest to 0 on its right and the maximum value at a point closest to 1 on its left. Are such points available? Of course, not. It is not possible to locate such points. Infact, if a point $x_0$ is closest to 0 , then we find $\frac{x_0}{2}<x_0$ for all $x_0 \in(0,1)$. Also, if $x_1$ is closest to 1 , then $\frac{x_1+1}{2}>x_1$ for all $x_1 \in(0,1)$.

Therefore, the given function has neither the

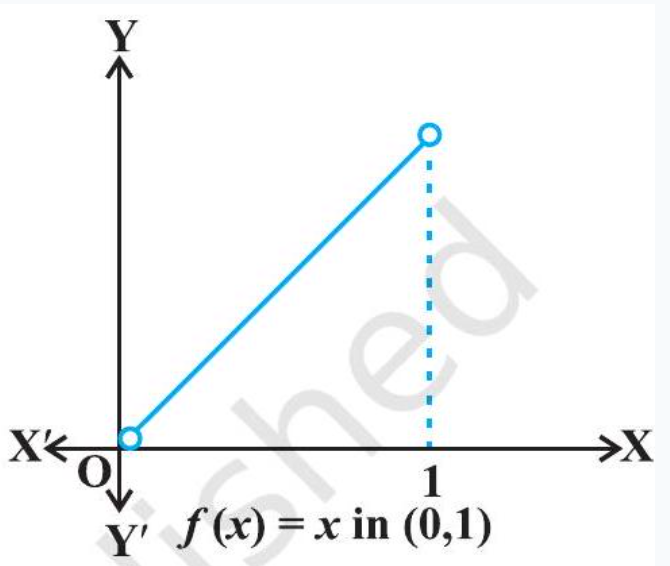
Fig 6.10 maximum value nor the minimum value in the interval $(0,1)$.

Remark The reader may observe that in Example 16 **, if we include the points 0 and 1 in the domain of $f$, i.e., if we extend the domain of $f$ to $[0,1]$, then the function $f$ has minimum value 0 at $x=0$ and maximum value 1 at $x=1$. Infact, we have the following results (The proof of these results are beyond the scope of the present text)

Every monotonic function assumes its maximum/minimum value at the end points of the domain of definition of the function.

A more general result is

Every continuous function on a closed interval has a maximum and a minimum value.

Note By a monotonic function $f$ in an interval $I$, we mean that $f$ is either increasing in I or decreasing in I.

Maximum and minimum values of a function defined on a closed interval will be discussed later in this section.

Let us now examine the graph of a function as shown in Fig 6.11. Observe that at points $A, B, C$ and $D$ on the graph, the function changes its nature from decreasing to increasing or vice-versa. These points may be called turning points of the given function. Further, observe that at turning points, the graph has either a little hill or a little valley. Roughly speaking, the function has minimum value in some neighbourhood (interval) of each of the points $A$ and $C$ which are at the bottom of their respective

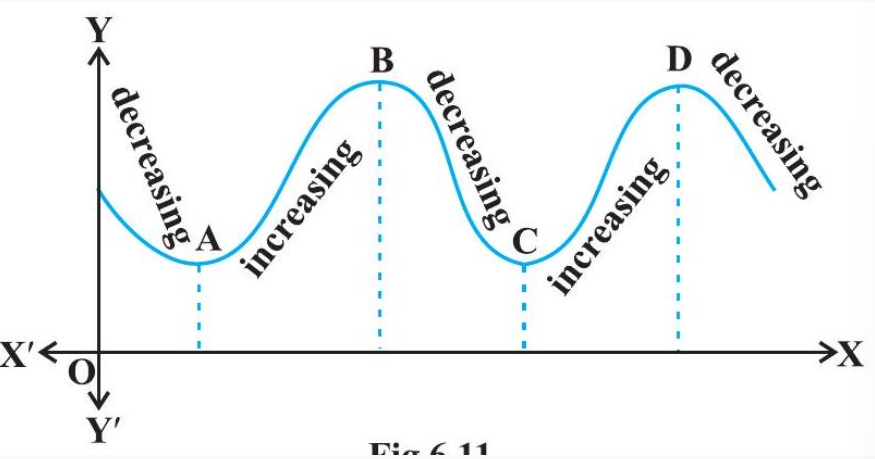
Fig 6.11

valleys. Similarly, the function has maximum value in some neighbourhood of points B and $D$ which are at the top of their respective hills. For this reason, the points $A$ and $C$ may be regarded as points of local minimum value (or relative minimum value) and points $B$ and $D$ may be regarded as points of local maximum value (or relative maximum value) for the function. The local maximum value and local minimum value of the function are referred to as local maxima and local minima, respectively, of the function.

We now formally give the following definition

Definition 4 Let $f$ be a real valued function and let $c$ be an interior point in the domain of $f$. Then

(a) $c$ is called a point of local maxima if there is an $h>0$ such that

$ f(c) \geq f(x) \text{, for all } x \text{ in }(c-h, c+h), x \neq c $

The value $f(c)$ is called the local maximum value of $f$.

(b) $c$ is called a point of local minima if there is an $h>0$ such that

$ f(c) \leq f(x) \text{, for all } x \text{ in }(c-h, c+h) $

The value $f(c)$ is called the local minimum value of $f$.

Geometrically, the above definition states that if $x=c$ is a point of local maxima of $f$, then the graph of $f$ around $c$ will be as shown in Fig 6.12(a). Note that the function $f$ is increasing (i.e., $.f^{\prime}(x)>0)$ in the interval $(c-h, c)$ and decreasing (i.e., $.f^{\prime}(x)<0)$ in the interval $(c, c+h)$.

This suggests that $f^{\prime}(c)$ must be zero.

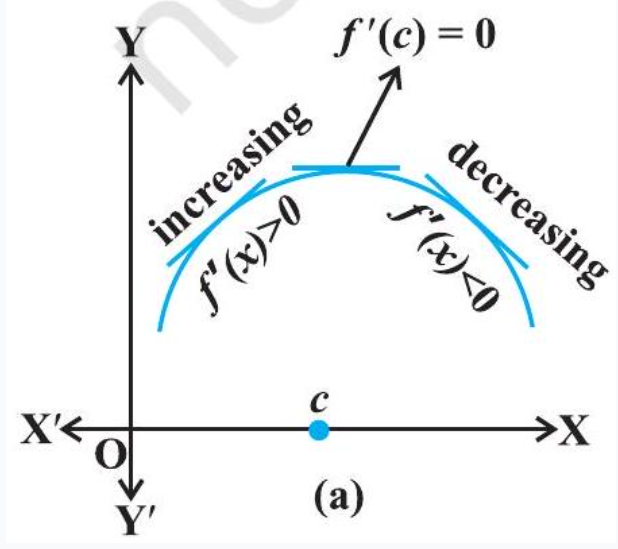
Fig 6.12

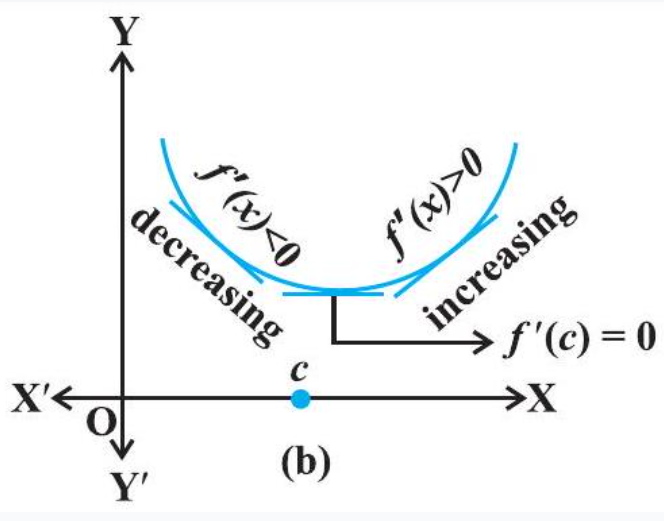
Similarly, if $c$ is a point of local minima of $f$, then the graph of $f$ around $c$ will be as shown in Fig 6.14(b). Here $f$ is decreasing (i.e., $.f^{\prime}(x)<0)$ in the interval $(c-h, c)$ and increasing (i.e., $.f^{\prime}(x)>0)$ in the interval $(c, c+h)$. This again suggest that $f^{\prime}(c)$ must be zero.

The above discussion lead us to the following theorem (without proof).

Theorem 2 Let $f$ be a function defined on an open interval I. Suppose $c \in I$ be any point. If $f$ has a local maxima or a local minima at $x=c$, then either $f^{\prime}(c)=0$ or $f$ is not differentiable at $c$.

Remark The converse of above theorem need not be true, that is, a point at which the derivative vanishes need not be a point of local maxima or local minima. For example, if $f(x)=x^{3}$, then $f^{\prime}(x)=3 x^{2}$ and so $f^{\prime}(0)=0$. But 0 is neither a point of local maxima nor a point of local minima (Fig 6.13).

Note A point $c$ in the domain of a function $f$ at which either $f^{\prime}(c)=0$ or $f$ is not differentiable is called a critical point of $f$. Note that if $f$ is continuous at $c$ and $f^{\prime}(c)=0$, then there exists an $h>0$ such that $f$ is differentiable in the interval $(c-h, c+h)$.

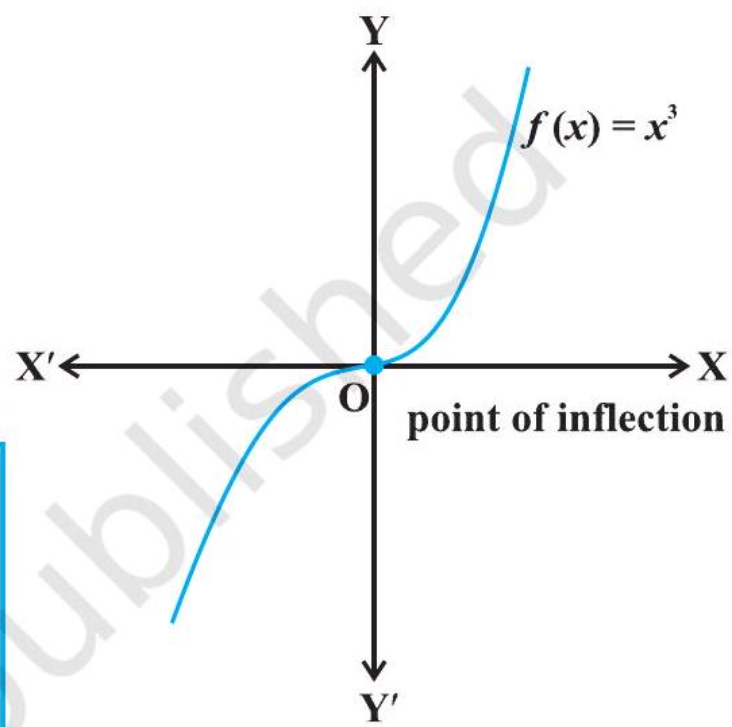
Fig 6.13

We shall now give a working rule for finding points of local maxima or points of local minima using only the first order derivatives.

Theorem 3 (First Derivative Test) Let $f$ be a function defined on an open interval I. Let $f$ be continuous at a critical point $c$ in I. Then

(i) If $f^{\prime}(x)$ changes sign from positive to negative as $x$ increases through $c$, i.e., if $f^{\prime}(x)>0$ at every point sufficiently close to and to the left of $c$, and $f^{\prime}(x)<0$ at every point sufficiently close to and to the right of $c$, then $c$ is a point of local maxima.

(ii) If $f^{\prime}(x)$ changes sign from negative to positive as $x$ increases through $c$, i.e., if $f^{\prime}(x)<0$ at every point sufficiently close to and to the left of $c$, and $f^{\prime}(x)>0$ at every point sufficiently close to and to the right of $c$, then $c$ is a point of local minima.

(iii) If $f^{\prime}(x)$ does not change sign as $x$ increases through $c$, then $c$ is neither a point of local maxima nor a point of local minima. Infact, such a point is called point of inflection (Fig 6.13).

Note If $c$ is a point of local maxima of $f$, then $f(c)$ is a local maximum value of $f$. Similarly, if $c$ is a point of local minima of $f$, then $f(c)$ is a local minimum value of $f$.

Figures 6.13 and 6.14, geometrically explain Theorem 3.

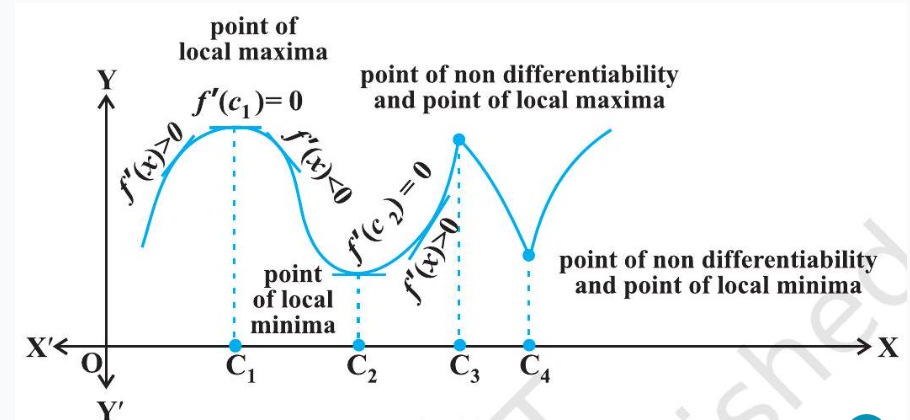
Fig 6.14

Example 17 Find all points of local maxima and local minima of the function $f$ given by

$ f(x)=x^{3}-3 x+3 . $

Solution We have

or

$ \begin{aligned} f(x) & =x^{3}-3 x+3 \\ f^{\prime}(x) & =3 x^{2}-3=3(x-1)(x+1) \\ f^{\prime}(x) & =0 \text{ at } x=1 \text{ and } x=-1 \end{aligned} $

or

Thus, $x= \pm 1$ are the only critical points which could possibly be the points of local maxima and/or local minima of $f$. Let us first examine the point $x=1$.

Note that for values close to 1 and to the right of $1, f^{\prime}(x)>0$ and for values close to 1 and to the left of $1, f^{\prime}(x)<0$. Therefore, by first derivative test, $x=1$ is a point of local minima and local minimum value is $f(1)=1$. In the case of $x=-1$, note that $f^{\prime}(x)>0$, for values close to and to the left of -1 and $f^{\prime}(x)<0$, for values close to and to the right of -1 . Therefore, by first derivative test, $x=-1$ is a point of local maxima and local maximum value is $f(-1)=5$.

Values of x	Sign of f’(x)=3(x-1)(x+1)
close to $ 1 \langle\begin{matrix} \text{to the right(say 1.1 etc.} ) \\ \text{to the left(say 0.9 etc) } \end{matrix} \rvert $ )	>0 <0
close to $ -1 \langle\begin{matrix} \text{to the right(say -0.9 etc.} ) \\ \text{to the left(say -1.1 etc) } \end{matrix} \rvert $ )	<0 >0

Example 18 Find all the points of local maxima and local minima of the function $f$ given by

Solution We have

$ f(x)=2 x^{3}-6 x^{2}+6 x+5 . $

or

$ \begin{aligned} f(x) & =2 x^{3}-6 x^{2}+6 x+5 \\ f^{\prime}(x) & =6 x^{2}-12 x+6=6(x-1)^{2} \\ f^{\prime}(x) & =0 \quad \text{ at } \quad x=1 \end{aligned} $

Thus, $x=1$ is the only critical point of $f$. We shall now examine this point for local maxima and/or local minima of $f$. Observe that $f^{\prime}(x) \geq 0$, for all $x \in \mathbf{R}$ and in particular $f^{\prime}(x)>0$, for values close to 1 and to the left and to the right of 1 . Therefore, by first derivative test, the point $x=1$ is neither a point of local maxima nor a point of local minima. Hence $x=1$ is a point of inflexion.

Remark One may note that since $f^{\prime}(x)$, in Example 30 , never changes its sign on $\mathbf{R}$, graph of $f$ has no turning points and hence no point of local maxima or local minima.

We shall now give another test to examine local maxima and local minima of a given function. This test is often easier to apply than the first derivative test.

Theorem 4 (Second Derivative Test) Let $f$ be a function defined on an interval I and $c \in I$. Let $f$ be twice differentiable at $c$. Then

(i) $x=c$ is a point of local maxima if $f^{\prime}(c)=0$ and $f^{\prime \prime}(c)<0$

The value $f(c)$ is local maximum value of $f$.

(ii) $x=c$ is a point of local minima if $f^{\prime}(c)=0$ and $f^{\prime \prime}(c)>0$

In this case, $f(c)$ is local minimum value of $f$.

(iii) The test fails if $f^{\prime}(c)=0$ and $f^{\prime \prime}(c)=0$.

In this case, we go back to the first derivative test and find whether $c$ is a point of local maxima, local minima or a point of inflexion.

Note As $f$ is twice differentiable at $c$, we mean second order derivative of $f$ exists at $c$.

Example 19 Find local minimum value of the function $f$ given by $f(x)=3+|x|, x \in \mathbf{R}$.

Solution Note that the given function is not differentiable at $x=0$. So, second derivative test fails. Let us try first derivative test. Note that 0 is a critical point of $f$. Now to the left of $0, f(x)=3-x$ and so $f^{\prime}(x)=-1<0$. Also to

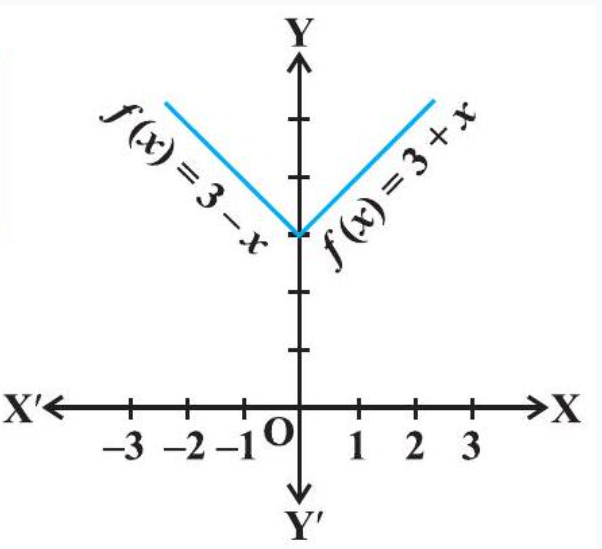
Fig 6.15 the right of $0, f(x)=3+x$ and so $f^{\prime}(x)=1>0$. Therefore, by first derivative test, $x=$ 0 is a point of local minima of $f$ and local minimum value of $f$ is $f(0)=3$.

Example 20 Find local maximum and local minimum values of the function $f$ given by

$ f(x)=3 x^{4}+4 x^{3}-12 x^{2}+12 $

Solution We have

$f(x)=3 x^{4}+4 x^{3}-12 x^{2}+12$

or & $f^{\prime}(x)=12 x^{3}+12 x^{2}-24 x=12 x(x-1)(x+2)$

or & $f^{\prime}(x)=0$ at $x=0, x=1$ and $x=-2$.

Now & $f^{\prime \prime}(x)=36 x^{2}+24 x-24=12(3 x^{2}+2 x-2)$

or$ \begin{cases} & f^{\prime \prime}(0)=-24<0 \\ &f^{\prime \prime}(1)=36>0 \\ & f^{\prime \prime}(-2)=72>0\end{cases} $

Therefore, by second derivative test, $x=0$ is a point of local maxima and local maximum value of $f$ at $x=0$ is $f(0)=12$ while $x=1$ and $x=-2$ are the points of local minima and local minimum values of $f$ at $x=-1$ and -2 are $f(1)=7$ and $f(-2)=-20$, respectively.

Example 21 Find all the points of local maxima and local minima of the function $f$ given by

$ f(x)=2 x^{3}-6 x^{2}+6 x+5 $

Solution We have

or

$ f(x)=2 x^{3}-6 x^{2}+6 x+5 $

or$\begin{cases} f^{\prime}(x)=6 x^{2}-12 x+6=6(x-1)^{2} \\ f^{\prime \prime}(x)=12(x-1) \end{cases}.$

Now $f^{\prime}(x)=0$ gives $x=1$. Also $f^{\prime \prime}(1)=0$. Therefore, the second derivative test fails in this case. So, we shall go back to the first derivative test.

We have already seen (Example 18 ) that, using first derivative test, $x=1$ is neither a point of local maxima nor a point of local minima and so it is a point of inflexion.

Example 22 Find two positive numbers whose sum is 15 and the sum of whose squares is minimum.

Solution Let one of the numbers be $x$. Then the other number is $(15-x)$. Let $S(x)$ denote the sum of the squares of these numbers. Then or

$ S(x)=x^{2}+(15-x)^{2}=2 x^{2}-30 x+225 $

$ \begin{cases} S^{\prime}(x)=4 x-30 \\ S^{\prime \prime}(x)=4.\end{cases} $

Now $S^{\prime}(x)=0$ gives $x=\frac{15}{2}$. Also $S^{\prime \prime}(\frac{15}{2})=4>0$. Therefore, by second derivative test, $x=\frac{15}{2}$ is the point of local minima of S. Hence the sum of squares of numbers is minimum when the numbers are $\frac{15}{2}$ and $15-\frac{15}{2}=\frac{15}{2}$.

Remark Proceeding as in Example 34 one may prove that the two positive numbers, whose sum is $k$ and the sum of whose squares is minimum, are $\frac{k}{2}$ and $\frac{k}{2}$.

Example 23 Find the shortest distance of the point $(0, c)$ from the parabola $y=x^{2}$, where $\frac{1}{2} \leq c \leq 5$.

Solution Let $(h, k)$ be any point on the parabola $y=x^{2}$. Let $D$ be the required distance between $(h, k)$ and $(0, c)$. Then

$ D=\sqrt{(h-0)^{2}+(k-c)^{2}}=\sqrt{h^{2}+(k-c)^{2}} $

Since $(h, k)$ lies on the parabola $y=x^{2}$, we have $k=h^{2}$. So (1) gives

$ D \equiv D(k)=\sqrt{k+(k-c)^{2}} $

or

$ D^{\prime}(k)=\frac{1+2(k-c)}{2 \sqrt{k+(k-c)^{2}}} $

Now

$ D^{\prime}(k)=0 \text{ gives } k=\frac{2 c-1}{2} $

Observe that when $k<\frac{2 c-1}{2}$, then $2(k-c)+1<0$, i.e., $D^{\prime}(k)<0$. Also when $k>\frac{2 c-1}{2}$, then $D^{\prime}(k)>0$. So, by first derivative test, $D(k)$ is minimum at $k=\frac{2 c-1}{2}$.

Hence, the required shortest distance is given by

$ D(\frac{2 c-1}{2})=\sqrt{\frac{2 c-1}{2}+(\frac{2 c-1}{2}-c)^{2}}=\frac{\sqrt{4 c-1}}{2} $

Note The reader may note that in Example 35 , we have used first derivative test instead of the second derivative test as the former is easy and short.

Example 24 Let $AP$ and $BQ$ be two vertical poles at points $A$ and $B$, respectively. If $AP=16 m, BQ=22 m$ and $A B=20 m$, then find the distance of a point $R$ on $A B$ from the point $A$ such that $R P^{2}+R Q^{2}$ is minimum.

Solution Let $R$ be a point on $AB$ such that $AR=x m$. Then $RB=(20-x) m($ as $AB=20 m)$. From Fig 6.16, we have

and

$ RP^{2}=AR^{2}+AP^{2} $

Therefore

$ R Q^{2}=R B^{2}+B Q^{2} $

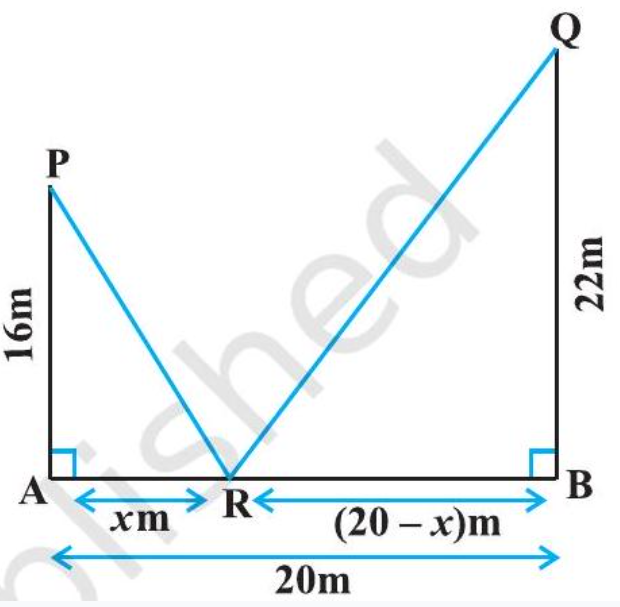
Fig 6.16

$ \begin{aligned} RP^{2}+RQ^{2} & =AR^{2}+AP^{2}+RB^{2}+BQ^{2} \\ & =x^{2}+(16)^{2}+(20-x)^{2}+(22)^{2} \\ & =2 x^{2}-40 x+1140 \end{aligned} $

Let

$ S \equiv S(x)=RP^{2}+RQ^{2}=2 x^{2}-40 x+1140 $

Therefore

$ S^{\prime}(x)=4 x-40 . $

Now $S^{\prime}(x)=0$ gives $x=10$. Also $S^{\prime \prime}(x)=4>0$, for all $x$ and so $S^{\prime \prime}(10)>0$. Therefore, by second derivative test, $x=10$ is the point of local minima of $S$. Thus, the distance of $R$ from $A$ on $AB$ is $AR=x=10 m$.

Example 25 If length of three sides of a trapezium other than base are equal to $10 cm$, then find the area of the trapezium when it is maximum.

Solution The required trapezium is as given in Fig 6.17. Draw perpendiculars DP and

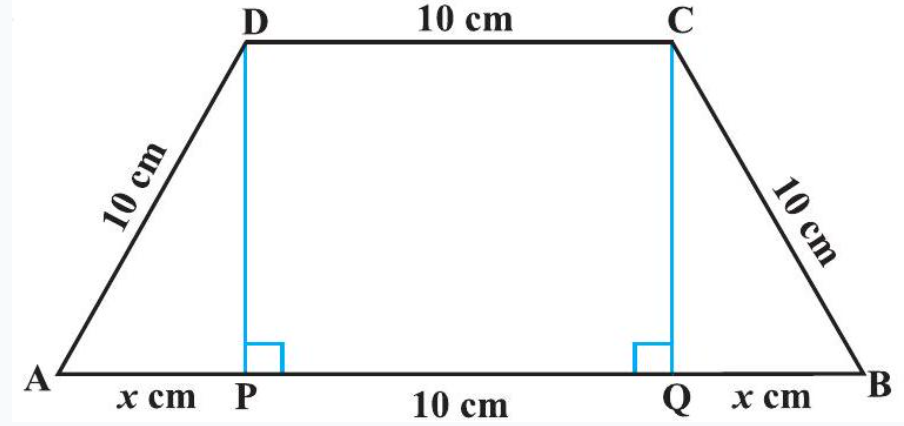
Fig 6.17 $CQ$ on $AB$. Let $AP=x cm$. Note that $\triangle APD \sim \triangle BQC$. Therefore, $QB=x cm$. Also, by Pythagoras theorem, $DP=QC=\sqrt{100-x^{2}}$. Let $A$ be the area of the trapezium. Then

$ \begin{aligned} A \equiv A(x) & =\frac{1}{2} \text{ (sum of parallel sides) (height) } \\ & =\frac{1}{2}(2 x+10+10)(\sqrt{100-x^{2}}) \\ & =(x+10)(\sqrt{100-x^{2}}) \\ A^{\prime}(x) & =(x+10) \frac{(-2 x)}{2 \sqrt{100-x^{2}}}+(\sqrt{100-x^{2}}) \\ & =\frac{-2 x^{2}-10 x+100}{\sqrt{100-x^{2}}} \end{aligned} $

or

Now $\quad A^{\prime}(x)=0$ gives $2 x^{2}+10 x-100=0$, i.e., $x=5$ and $x=-10$.

Since $x$ represents distance, it can not be negative.

So, $x=5$. Now

$ \begin{aligned} A^{\prime \prime}(x) & =\frac{\sqrt{100-x^{2}}(-4 x-10)-(-2 x^{2}-10 x+100) \frac{(-2 x)}{2 \sqrt{100-x^{2}}}}{100-x^{2}} \\ & =\frac{2 x^{3}-300 x-1000}{(100-x^{2})^{\frac{3}{2}}} \text{ (on simplification) } \\ A^{\prime \prime}(5) & =\frac{2(5)^{3}-300(5)-1000}{(100-(5)^{2})^{\frac{3}{2}}}=\frac{-2250}{75 \sqrt{75}}=\frac{-30}{\sqrt{75}}<0 \end{aligned} $

Thus, area of trapezium is maximum at $x=5$ and the area is given by

$ A(5)=(5+10) \sqrt{100-(5)^{2}}=15 \sqrt{75}=75 \sqrt{3} cm^{2} $

Example 26 Prove that the radius of the right circular cylinder of greatest curved surface area which can be inscribed in a given cone is half of that of the cone.

Solution Let $OC=r$ be the radius of the cone and $OA=h$ be its height. Let a cylinder with radius $OE=x$ inscribed in the given cone (Fig 6.18). The height $QE$ of the cylinder is given by

$ \begin{aligned} & \frac{QE}{OA} & =\frac{EC}{OC} \quad(\text{ since } \Delta QEC \sim \Delta AOC) \\ \text{ or } & \frac{QE}{h} & =\frac{r-x}{r} \\ \text{ or } & QE & =\frac{h(r-x)}{r} \end{aligned} $

Let $S$ be the curved surface area of the given cylinder. Then

$ S \equiv S(x)=\frac{2 \pi x h(r-x)}{r}=\frac{2 \pi h}{r}(r x-x^{2}) $

$ \begin{cases} S^{\prime}(x)=\frac{2 \pi h}{r}(r-2 x) \\ S^{\prime \prime}(x)=\frac{-4 \pi h}{r} .\end{cases} $

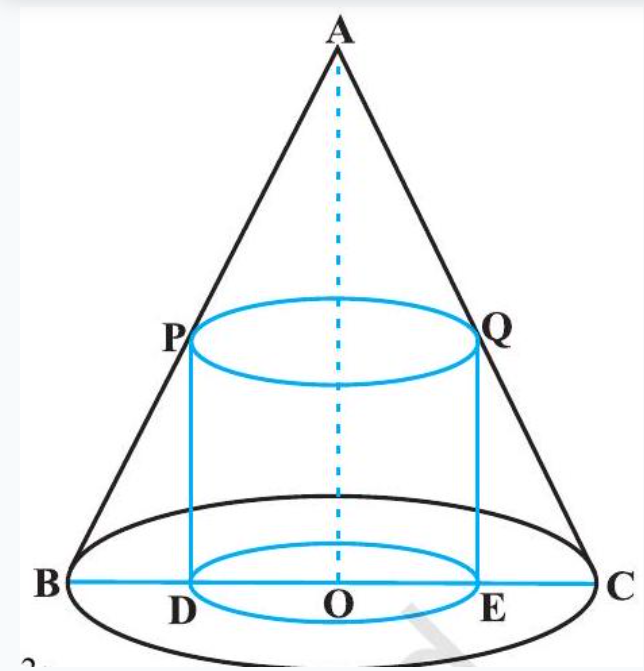
Fig 6.18

or

Now $S^{\prime}(x)=0$ gives $x=\frac{r}{2}$. Since $S^{\prime \prime}(x)<0$ for all $x, S^{\prime \prime}(\frac{r}{2})<0$. So $x=\frac{r}{2}$ is a point of maxima of S. Hence, the radius of the cylinder of greatest curved surface area which can be inscribed in a given cone is half of that of the cone.

6.4.1 Maximum and Minimum Values of a Function in a Closed Interval

Let us consider a function $f$ given by

$ f(x)=x+2, x \in(0,1) $

Observe that the function is continuous on $(0,1)$ and neither has a maximum value nor has a minimum value. Further, we may note that the function even has neither a local maximum value nor a local minimum value.

However, if we extend the domain of $f$ to the closed interval $[0,1]$, then $f$ still may not have a local maximum (minimum) values but it certainly does have maximum value $3=f(1)$ and minimum value $2=f(0)$. The maximum value 3 of $f$ at $x=1$ is called absolute maximum value (global maximum or greatest value) of $f$ on the interval $[0,1]$. Similarly, the minimum value 2 of $f$ at $x=0$ is called the absolute minimum value (global minimum or least value) of $f$ on $[0,1]$.

Consider the graph given in Fig 6.19 of a continuous function defined on a closed interval $[a, d]$. Observe that the function $f$ has a local minima at $x=b$ and local

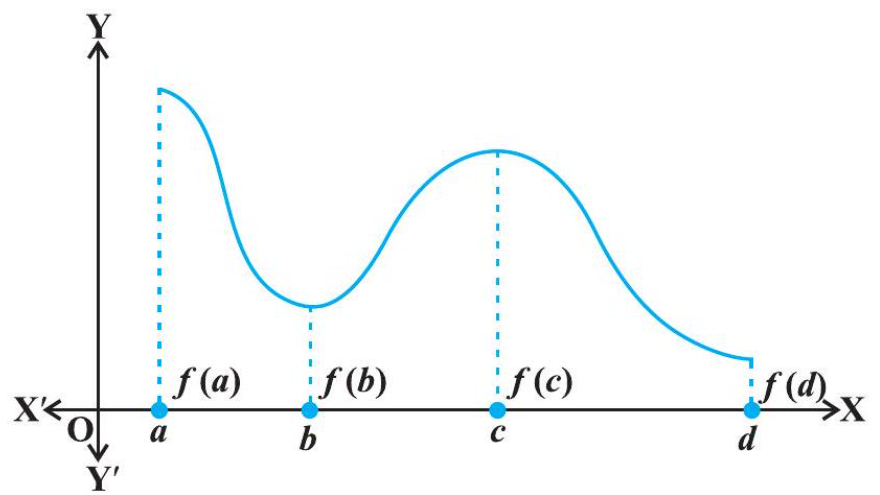
Fig 6.19

minimum value is $f(b)$. The function also has a local maxima at $x=c$ and local maximum value is $f(c)$.

Also from the graph, it is evident that $f$ has absolute maximum value $f(a)$ and absolute minimum value $f(d)$. Further note that the absolute maximum (minimum) value of $f$ is different from local maximum (minimum) value of $f$.

We will now state two results (without proof) regarding absolute maximum and absolute minimum values of a function on a closed interval I.

Theorem 5 Let $f$ be a continuous function on an interval $I=[a, b]$. Then $f$ has the absolute maximum value and $f$ attains it at least once in I. Also, $f$ has the absolute minimum value and attains it at least once in $I$.

Theorem 6 Let $f$ be a differentiable function on a closed interval I and let $c$ be any interior point of I. Then

(i) $f^{\prime}(c)=0$ if $f$ attains its absolute maximum value at $c$.

(ii) $f^{\prime}(c)=0$ if $f$ attains its absolute minimum value at $c$.

In view of the above results, we have the following working rule for finding absolute maximum and/or absolute minimum values of a function in a given closed interval $[a, b]$.

Working Rule

Step 1: Find all critical points of $f$ in the interval, i.e., find points $x$ where either $f^{\prime}(x)=0$ or $f$ is not differentiable.

Step 2: Take the end points of the interval.

Step 3: At all these points (listed in Step 1 and 2), calculate the values of $f$.

Step 4: Identify the maximum and minimum values of $f$ out of the values calculated in Step 3. This maximum value will be the absolute maximum (greatest) value of $f$ and the minimum value will be the absolute minimum (least) value of $f$.

Example 27 Find the absolute maximum and minimum values of a function $f$ given by

$ f(x)=2 x^{3}-15 x^{2}+36 x+1 \text{ on the interval }[1,5] . $

Solution We have

or

$ \begin{aligned} f(x) & =2 x^{3}-15 x^{2}+36 x+1 \\ f^{\prime}(x) & =6 x^{2}-30 x+36=6(x-3)(x-2) \end{aligned} $

Note that $f^{\prime}(x)=0$ gives $x=2$ and $x=3$.

We shall now evaluate the value of $f$ at these points and at the end points of the interval $[1,5]$, i.e., at $x=1, x=2, x=3$ and at $x=5$. So

$ \begin{aligned} & f(1)=2(1^{3})-15(1^{2})+36(1)+1=24 \\ & f(2)=2(2^{3})-15(2^{2})+36(2)+1=29 \\ & f(3)=2(3^{3})-15(3^{2})+36(3)+1=28 \\ & f(5)=2(5^{3})-15(5^{2})+36(5)+1=56 \end{aligned} $

Thus, we conclude that absolute maximum value of $f$ on $[1,5]$ is 56 , occurring at $x=5$, and absolute minimum value of $f$ on $[1,5]$ is 24 which occurs at $x=1$.

Example 28 Find absolute maximum and minimum values of a function $f$ given by

$ f(x)=12 x^{\frac{4}{3}}-6 x^{\frac{1}{3}}, x \in[-1,1] $

Solution We have

or

$ f(x)=12 x^{\frac{4}{3}}-6 x^{\frac{1}{3}} $

$ f^{\prime}(x)=16 x^{\frac{1}{3}}-\frac{2}{x^{\frac{2}{3}}}=\frac{2(8 x-1)}{x^{\frac{2}{3}}} $

Thus, $f^{\prime}(x)=0$ gives $x=\frac{1}{8}$. Further note that $f^{\prime}(x)$ is not defined at $x=0$. So the critical points are $x=0$ and $x=\frac{1}{8}$. Now evaluating the value of $f$ at critical points $x=0, \frac{1}{8}$ and at end points of the interval $x=-1$ and $x=1$, we have

$ \begin{aligned} f(-1) & =12(-1)^{\frac{4}{3}}-6(-1)^{\frac{1}{3}}=18 \\ f(0) & =12(0)-6(0)=0 \end{aligned} $

$ \begin{aligned} f(\frac{1}{8}) & =12(\frac{1}{8})^{\frac{4}{3}}-6(\frac{1}{8})^{\frac{1}{3}}=\frac{-9}{4} \\ f(1) & =12(1)^{\frac{4}{3}}-6(1)^{\frac{1}{3}}=6 \end{aligned} $

Hence, we conclude that absolute maximum value of $f$ is 18 that occurs at $x=-1$ and absolute minimum value of $f$ is $\frac{-9}{4}$ that occurs at $x=\frac{1}{8}$.

Example 29 An Apache helicopter of enemy is flying along the curve given by $y=x^{2}+7$. A soldier, placed at $(3,7)$, wants to shoot down the helicopter when it is nearest to him. Find the nearest distance.

Solution For each value of $x$, the helicopter’s position is at point $(x, x^{2}+7)$. Therefore, the distance between the helicopter and the soldier placed at $(3,7)$ is

$ \sqrt{(x-3)^{2}+(x^{2}+7-7)^{2}} \text{, i.e., } \sqrt{(x-3)^{2}+x^{4}} \text{. } $

Let

$ f(x)=(x-3)^{2}+x^{4} $

or

$ f^{\prime}(x)=2(x-3)+4 x^{3}=2(x-1)(2 x^{2}+2 x+3) $

Thus, $f^{\prime}(x)=0$ gives $x=1$ or $2 x^{2}+2 x+3=0$ for which there are no real roots. Also, there are no end points of the interval to be added to the set for which $f^{\prime}$ is zero, i.e., there is only one point, namely, $x=1$. The value of $f$ at this point is given by $f(1)=(1-3)^{2}+(1)^{4}=5$. Thus, the distance between the solider and the helicopter is $\sqrt{f(1)}=\sqrt{5}$.

Note that $\sqrt{5}$ is either a maximum value or a minimum value. Since

$ \sqrt{f(0)}=\sqrt{(0-3)^{2}+(0)^{4}}=3>\sqrt{5}, $

it follows that $\sqrt{5}$ is the minimum value of $\sqrt{f(x)}$. Hence, $\sqrt{5}$ is the minimum distance between the soldier and the helicopter.

EXERCISE 6.3

1. Find the maximum and minimum values, if any, of the following functions given by

(i) $f(x)=(2 x-1)^{2}+3$

(ii) $f(x)=9 x^{2}+12 x+2$

(iii) $f(x)=-(x-1)^{2}+10$

(iv) $g(x)=x^{3}+1$

Solution

(i) The given function is $f(x)=(2 x-1)^{2}+3$.

It can be observed that $(2 x-1)^{2} \geq 0$ for every $x \square \mathbf{R}$.

Therefore, $f(x)=(2 x-1)^{2}+3 \geq 3$ for every $x \square \mathbf{R}$.

The minimum value of $f$ is attained when $2 x-1=0$.

$2 x-1=0$

$ x=\frac{1}{2} $

$\square$ Minimum value of $f=f(\frac{1}{2})=(2 \cdot \frac{1}{2}-1)^{2}+3=3$

Hence, function $f$ does not have a maximum value.

(ii) The given function is $f(x)=9 x^{2}+12 x+2=(3 x+2)^{2}-2$.

It can be observed that $(3 x+2)^{2} \geq 0$ for every $x \square \mathbf{R}$.

Therefore, $f(x)=(3 x+2)^{2}-2 \geq-2$ for every $x \square \mathbf{R}$.

The minimum value of $f$ is attained when $3 x+2=0$.

$3 x+2=0 \square^{x=\frac{-2}{3}}$

$\square$ Minimum value of $f=f(-\frac{2}{3})=(3(\frac{-2}{3})+2)^{2}-2=-2$

Hence, function $f$ does not have a maximum value.

(iii) The given function is $f(x)=-(x-1)^{2}+10$.

It can be observed that $(x-1)^{2} \geq 0$ for every $x \square \mathbf{R}$.

Therefore, $f(x)=-(x-1)^{2}+10 \leq 10$ for every $x \square \mathbf{R}$.

The maximum value of $f$ is attained when $(x-1)=0$.

$(x-1)=0 \square x=0$

$\square$ Maximum value of $f=f(1)=-(1-1)^{2}+10=10$

Hence, function $f$ does not have a minimum value.

(iv) The given function is $g(x)=x^{3}+1$.

Hence, function $g$ neither has a maximum value nor a minimum value.

2. Find the maximum and minimum values, if any, of the following functions given by

(i) $f(x)=|x+2|-1$

(ii) $g(x)=-|x+1|+3$

(iii) $h(x)=\sin (2 x)+5$

(iv) $f(x)=|\sin 4 x+3|$

(v) $h(x)=x+1, x \in(-1,1)$

Solution

(i) $f(x)=|x+2|-1$

We know that $|x+2| \geq 0$ for every $x \square \mathbf{R}$.

Therefore, $f(x)=|x+2|-1 \geq-1$ for every $x \square \mathbf{R}$.

The minimum value of $f$ is attained when $|x+2|=0$.

$|x+2|=0$

$\Rightarrow x=-2$

$\square$ Minimum value of $f=f(-2)=|-2+2|-1=-1$

Hence, function $f$ does not have a maximum value.

(ii) $g(x)=-|x+1|+3$

We know that $-|x+1| \leq 0$ for every $x \square \mathbf{R}$.

Therefore, $g(x)=-|x+1|+3 \leq 3$ for every $x \square \mathbf{R}$.

The maximum value of $g$ is attained when $|x+1|=0$.

$|x+1|=0$

$\Rightarrow x=-1$

$\square$ Maximum value of $g=g(-1)=-|-1+1|+3=3$

Hence, function $g$ does not have a minimum value. (iii) $h(x)=\sin 2 x+5$

We know that $-1 \leq \sin 2 x \leq 1$.

$\square-1+5 \leq \sin 2 x+5 \leq 1+5$

$\square 4 \leq \sin 2 x+5 \leq 6$

Hence, the maximum and minimum values of $h$ are 6 and 4 respectively.

(iv) $f(x)=|\sin 4 x+3|$

We know that $-1 \leq \sin 4 x \leq 1$.

$\square 2 \leq \sin 4 x+3 \leq 4$

$\square 2 \leq^{|\sin 4 x+3|} \leq 4$

Hence, the maximum and minimum values of $f$ are 4 and 2 respectively.

(v) $h(x)=x+1, x \square(-1,1)$

Here, if a point $x_0$ is closest to -1 , then we find $\frac{x_0}{2}+1<x_0+1$ for all $x_0 \square(-1,1)$.

Also, if $x_1$ is closest to 1 , then $x_1+1<\frac{x_1+1}{2}+1$ for all $x_1 \square(-1,1)$.

Hence, function $h(x)$ has neither maximum nor minimum value in $(-1,1)$.

3. Find the local maxima and local minima, if any, of the following functions. Find also the local maximum and the local minimum values, as the case may be:

(i) $f(x)=x^{2}$

(ii) $g(x)=x^{3}-3 x$

(iii) $h(x)=\sin x+\cos x, 0<x<\frac{\pi}{2}$

(iv) $f(x)=\sin x-\cos x, 0<x<2 \pi$

(v) $f(x)=x^{3}-6 x^{2}+9 x+15 \quad$ (vi) $g(x)=\frac{x}{2}+\frac{2}{x}, x>0$

(vii) $g(x)=\frac{1}{x^{2}+2}$

(viii) $f(x)=x \sqrt{1-x}, 0<x<1$

Solution

(i) $f(x)=x^{2}$

$\therefore f^{\prime}(x)=2 x$

Now,

$f^{\prime}(x)=0 \Rightarrow x=0$

Thus, $x=0$ is the only critical point which could possibly be the point of local maxima or local minima of $f$.

We have $f^{\prime \prime}(0)=2$, which is positive.

Therefore, by second derivative test, $x=0$ is a point of local minima and local minimum value of $f$ at $x=0$ is $f(0)=0$.

(ii) $g(x)=x^{3}-3 x$

$\therefore g^{\prime}(x)=3 x^{2}-3$

Now,

$g^{\prime}(x)=0 \Rightarrow 3 x^{2}=3 \Rightarrow x= \pm 1$

$g^{\prime}(x)=6 x$

$g^{\prime}(1)=6>0$

$g^{\prime}(-1)=-6<0$

By second derivative test, $x=1$ is a point of local minima and local minimum value of $g$ at $x=1$ is $g(1)=1^{3}-3=1-3=-2$. However, $x=-1$ is a point of local maxima and local maximum value of $g$ at $x=-1$ is $g(1)=(-1)^{3}-3(-1)=-1+3=2$.

(iii) $h(x)=\sin x+\cos x, 0<x<\frac{\pi}{2}$

$\therefore h^{\prime}(x)=\cos x-\sin x$

$h^{\prime}(x)=0 \Rightarrow \sin x=\cos x \Rightarrow \tan x=1 \Rightarrow x=\frac{\pi}{4} \in(0, \frac{\pi}{2})$

$h^{\prime \prime}(x)=-\sin x-\cos x=-(\sin x+\cos x)$

$h^{\prime \prime}(\frac{\pi}{4})=-(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}})=-\frac{2}{\sqrt{2}}=-\sqrt{2}<0$

Therefore, by second derivative test, $x=\frac{\pi}{4}$ is a point of local maxima and the local

maximum value of $h$ at $x=\frac{\pi}{4}$ is $h(\frac{\pi}{4})=\sin \frac{\pi}{4}+\cos \frac{\pi}{4}=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\sqrt{2}$.

(iv) $f(x)=\sin x-\cos x, 0<x<2 \pi$

$\therefore f^{\prime}(x)=\cos x+\sin x$

$f^{\prime}(x)=0 \Rightarrow \cos x=-\sin x \Rightarrow \tan x=-1 \Rightarrow x=\frac{3 \pi}{4}, \frac{7 \pi}{4} \in(0,2 \pi)$

$f^{\prime \prime}(x)=-\sin x+\cos x$

$f^{\prime \prime}(\frac{3 \pi}{4})=-\sin \frac{3 \pi}{4}+\cos \frac{3 \pi}{4}=-\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}=-\sqrt{2}>0$

$f^{\prime \prime}(\frac{7 \pi}{4})=-\sin \frac{7 \pi}{4}+\cos \frac{7 \pi}{4}=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\sqrt{2}>0$

Therefore, by second derivative test, $x=\frac{3 \pi}{4}$ is a point of local maxima and the local

maximum value of $f$ at $x=\frac{3 \pi}{4}$ is

$f(\frac{3 \pi}{4})=\sin \frac{3 \pi}{4}-\cos \frac{3 \pi}{4}=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\sqrt{2}$ However, $x=\frac{7 \pi}{4}$ is a point of local minima and

the local minimum value of $f$ at $x=\frac{7 \pi}{4}$ is $f(\frac{7 \pi}{4})=\sin \frac{7 \pi}{4}-\cos \frac{7 \pi}{4}=-\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}=-\sqrt{2}$.

(v) $f(x)=x^{3}-6 x^{2}+9 x+15$

$\therefore f^{\prime}(x)=3 x^{2}-12 x+9$

$f^{\prime}(x)=0 \Rightarrow 3(x^{2}-4 x+3)=0$

$\Rightarrow 3(x-1)(x-3)=0$

$\Rightarrow x=1,3$

Now, $f^{\prime \prime}$

$(x)=6 x-12=6(x-2)$

$f^{\prime \prime}(1)=6(1-2)=-6<0$

$f^{\prime \prime}(3)=6(3-2)=6>0$

Therefore, by second derivative test, $x=1$ is a point of local maxima and the local maximum value of $f$ at $x=1$ is $f(1)=1-6+9+15=19$. However, $x=3$ is a point of local minima and the local minimum value of $f$ at $x=3$ is $f(3)=27-54+27+15=$ 15.

(vi) $g(x)=\frac{x}{2}+\frac{2}{x}, x>0$

$\therefore g^{\prime}(x)=\frac{1}{2}-\frac{2}{x^{2}}$

Now,

$g^{\prime}(x)=0$ gives $\frac{2}{x^{2}}=\frac{1}{2} \Rightarrow x^{2}=4 \Rightarrow x= \pm 2$

Since $x>0$, we take $x=2$.

Now,

$g^{\prime \prime}(x)=\frac{4}{x^{3}}$

$g^{\prime \prime}(2)=\frac{4}{2^{3}}=\frac{1}{2}>0$

Therefore, by second derivative test, $x=2$ is a point of local minima and the local

minimum value of $g$ at $x=2$ is $g(2)=\frac{2}{2}+\frac{2}{2}=1+1=2$.

(vii) $g(x)=\frac{1}{x^{2}+2}$

$\therefore g^{\prime}(x)=\frac{-(2 x)}{(x^{2}+2)^{2}}$

$g^{\prime}(x)=0 \Rightarrow \frac{-2 x}{(x^{2}+2)^{2}}=0 \Rightarrow x=0$

Now, for values close to $x=0$ and to the left of $0, g^{\prime}(x)>0$. Also, for values close to $x=$ 0 and to the right of $0, g^{\prime}(x)<0$.

Therefore, by first derivative test, $x=0$ is a point of local maxima and the local maximum value of $g(0)$ is $\frac{1}{0+2}=\frac{1}{2}$.

(viii) $f(x)=x \sqrt{1-x}, x>0$

$\therefore f^{\prime}(x)=\sqrt{1-x}+x \cdot \frac{1}{2 \sqrt{1-x}}(-1)=\sqrt{1-x}-\frac{x}{2 \sqrt{1-x}}$

$=\frac{2(1-x)-x}{2 \sqrt{1-x}}=\frac{2-3 x}{2 \sqrt{1-x}}$

$f^{\prime}(x)=0 \Rightarrow \frac{2-3 x}{2 \sqrt{1-x}}=0 \Rightarrow 2-3 x=0 \Rightarrow x=\frac{2}{3}$

$f^{\prime \prime}(x)=\frac{1}{2}[\frac{\sqrt{1-x}(-3)-(2-3 x)(\frac{-1}{2 \sqrt{1-x}})}{1-x}]$

$=\frac{\sqrt{1-x}(-3)+(2-3 x)(\frac{1}{2 \sqrt{1-x}})}{2(1-x)}$

$=\frac{-6(1-x)+(2-3 x)}{4(1-x)^{\frac{3}{2}}}$

$=\frac{3 x-4}{4(1-x)^{\frac{3}{2}}}$

$f^{\prime \prime}(\frac{2}{3})=\frac{3(\frac{2}{3})-4}{4(1-\frac{2}{3})^{\frac{3}{2}}}=\frac{2-4}{4(\frac{1}{3})^{\frac{3}{2}}}=\frac{-1}{2(\frac{1}{3})^{\frac{3}{2}}}<0$

Therefore, by second derivative test, $x=\frac{2}{3}$ is a point of local maxima and the local

maximum value of $f$ at $x=\frac{2}{3}$ is $f(\frac{2}{3})=\frac{2}{3} \sqrt{1-\frac{2}{3}}=\frac{2}{3} \sqrt{\frac{1}{3}}=\frac{2}{3 \sqrt{3}}=\frac{2 \sqrt{3}}{9}$.

4. Prove that the following functions do not have maxima or minima:

(i) $f(x)=e^{x}$

(ii) $g(x)=\log x$

(iii) $h(x)=x^{3}+x^{2}+x+1$

Solution

i. We have,

$f(x)=e^{x}$

$\therefore f^{\prime}(x)=e^{x}$

Now, if $f^{\prime}(x)=0$, then $e^{x}=0$. But, the exponential function can never assume 0 for any value of $x$.

Therefore, there does not exist $c \square \mathbf{R}$ such that $f^{\prime}(c)=0$.

Hence, function $f$ does not have maxima or minima.

ii. We have,

$g(x)=\log x$

$\therefore g^{\prime}(x)=\frac{1}{x}$

Since $\log x$ is defined for a positive number $x, g^{\prime}(x)>0$ for any $x$.

Therefore, there does not exist $c \square \mathbf{R}$ such that $g^{\prime}(c)=0$.

Hence, function $g$ does not have maxima or minima.

iii. We have,

$h(x)=x^{3}+x^{2}+x+1$

$\therefore h^{\prime}(x)=3 x^{2}+2 x+1$

Now,

$h(x)=0 \square 3 x^{2}+2 x+1=0 \square x=\frac{-2 \pm 2 \sqrt{2} i}{6}=\frac{-1 \pm \sqrt{2} i}{3} \notin \mathbf{R}$

Therefore, there does not exist $c \square \mathbf{R}$ such that $h^{\prime}(c)=0$.

Hence, function $h$ does not have maxima or minima.

5. Find the absolute maximum value and the absolute minimum value of the following functions in the given intervals:

(i) $f(x)=x^{3}, x \in[-2,2]$

(ii) $f(x)=\sin x+\cos x, x \in[0, \pi]$

(iii) $f(x)=4 x-\frac{1}{2} x^{2}, x \in[-2, \frac{9}{2}]$

(iv) $.f(x)=(x-1)^{2}+3, x \in-3,1]$

Solution

(i) The given function is $f(x)=x^{3}$.

$\therefore f^{\prime}(x)=3 x^{2}$

Now,

$f^{\prime}(x)=0 \Rightarrow x=0$

Then, we evaluate the value of $f$ at critical point $x=0$ and at end points of the interval $[-2,2]$.

$f(0)=0$

$f(-2)=(-2)^{3}=-8$

$f(2)=(2)^{3}=8$

Hence, we can conclude that the absolute maximum value of $f$ on $[-2,2]$ is 8 occurring at $x=2$. Also, the absolute minimum value of $f$ on $[-2,2]$ is -8 occurring at $x=-2$.

(ii) The given function is $f(x)=\sin x+\cos x$.

$\therefore f^{\prime}(x)=\cos x-\sin x$

Now,

$f^{\prime}(x)=0 \Rightarrow \sin x=\cos x \Rightarrow \tan x=1 \Rightarrow x=\frac{\pi}{4}$

Then, we evaluate the value of $f$ at critical point $x=\frac{\pi}{4}$ and at the end points of the interval $[0, \pi]$.

6. Find the maximum profit that a company can make, if the profit function is given by

$ p(x)=41-72 x-18 x^{2} $

Solution

The profit function is given as $p(x)=41-24 x-18 x^{2}$.

$\therefore p^{\prime}(x)=-24-36 x$

$p^{\prime \prime}(x)=-36$

Now,

$p^{\prime}(x)=0 \Rightarrow x=\frac{-24}{36}=-\frac{2}{3}$

Also,

$p^{\prime \prime}(\frac{-2}{3})=-36<0$

By second derivative test, $x=-\frac{2}{3}$ is the point of local maxima of $p$.

$\therefore$ Maximum profit $=p(-\frac{2}{3})$

$ \begin{aligned} & =41-24(-\frac{2}{3})-18(-\frac{2}{3})^{2} \\ & =41+16-8 \\ & =49 \end{aligned} $

Hence, the maximum profit that the company can make is 49 units.

7. Find both the maximum value and the minimum value of $3 x^{4}-8 x^{3}+12 x^{2}-48 x+25$ on the interval $[0,3]$.

Solution

$f(x)=3 x^4-8 x^3+12 x^2-48 x+25$

$f^{\prime}(x)=0$ for finding critical points

$f^{\prime}(x)=12 x^3-24 x^2+24 x-48$

$12 x^3-24 x^2+24 x-48=0$

$12 x^2(x-2)+24(x-2)=0$

$\left(12 x^2+24\right)(x-2)=0$

Since $12 x^2+24 \neq 0$ and $x-2=0 \Longrightarrow x=2$

We need to check at $x=0,2,3$ $f(0)=25$

$f(2)=-39$

$f(3)=16$

$\therefore$ Maximum of $f(x)$ at $x=0$ is 25

Minimum of $f(x)$ at $x=2$ is -39

8. At what points in the interval $[0,2 \pi]$, does the function $\sin 2 x$ attain its maximum value?

Solution

Let $f(x)=\sin 2 x$.

$\therefore f^{\prime}(x)=2 \cos 2 x$

Now,

$ \begin{aligned} & f^{\prime}(x)=0 \Rightarrow \cos 2 x=0 \\ & \Rightarrow 2 x=\frac{\pi}{2}, \frac{3 \pi}{2}, \frac{5 \pi}{2}, \frac{7 \pi}{2} \\ & \Rightarrow x=\frac{\pi}{4}, \frac{3 \pi}{4}, \frac{5 \pi}{4}, \frac{7 \pi}{4} \end{aligned} $

Then, we evaluate the values of $f$ at critical points $x=\frac{\pi}{4}, \frac{3 \pi}{4}, \frac{5 \pi}{4}, \frac{7 \pi}{4}$ and at the end points of the interval $[0,2 \pi]$.

$f(\frac{\pi}{4})=\sin \frac{\pi}{2}=1, f(\frac{3 \pi}{4})=\sin \frac{3 \pi}{2}=-1$

$f(\frac{5 \pi}{4})=\sin \frac{5 \pi}{2}=1, f(\frac{7 \pi}{4})=\sin \frac{7 \pi}{2}=-1$

$f(0)=\sin 0=0, f(2 \pi)=\sin 2 \pi=0$

Hence, we can conclude that the absolute maximum value of $f$ on $[0,2 \pi]$ is occurring

at $x=\frac{\pi}{4}$ and $\quad x=\frac{5 \pi}{4}$.

9. What is the maximum value of the function $\sin x+\cos x$ ?

Solution

Let $f(x)=\sin x+\cos x$.

$\therefore f^{\prime}(x)=\cos x-\sin x$

$f^{\prime}(x)=0 \Rightarrow \sin x=\cos x \Rightarrow \tan x=1 \Rightarrow x=\frac{\pi}{4}, \frac{5 \pi}{4} \ldots$,

$f^{\prime \prime}(x)=-\sin x-\cos x=-(\sin x+\cos x)$

Now, $f^{\prime \prime}(x)$ will be negative when $(\sin x+\cos x)$ is positive i.e., when $\sin x$ and $\cos x$ are both positive. Also, we know that $\sin x$ and $\cos x$ both are positive in the first

quadrant. Then, $f^{\prime \prime}(x)$ will be negative when $x \in(0, \frac{\pi}{2})$.

Thus, we consider $x=\frac{\pi}{4}$.

$f^{\prime \prime}(\frac{\pi}{4})=-(\sin \frac{\pi}{4}+\cos \frac{\pi}{4})=-(\frac{2}{\sqrt{2}})=-\sqrt{2}<0$ $\square$ By second derivative test, $f$ will be the maximum at $x=\frac{\pi}{4}$ and the maximum value of $f$ is $f(\frac{\pi}{4})=\sin \frac{\pi}{4}+\cos \frac{\pi}{4}=\frac{1}{\sqrt{2}} \times \frac{1}{\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}$.

10. Find the maximum value of $2 x^{3}-24 x+107$ in the interval $[1,3]$. Find the maximum value of the same function in $[-3,-1]$.

Solution

Let $f(x)=2 x^{3}-24 x+107$.

$\therefore f^{\prime}(x)=6 x^{2}-24=6(x^{2}-4)$

Now,

$f^{\prime}(x)=0 \Rightarrow 6(x^{2}-4)=0 \Rightarrow x^{2}=4 \Rightarrow x= \pm 2$

We first consider the interval $[1,3]$.

Then, we evaluate the value of $f$ at the critical point $x=2 \square[1,3]$ and at the end points of the interval $[1,3]$.

$f(2)=2(8)-24(2)+107=16-48+107=75$

$f(1)=2(1)-24(1)+107=2-24+107=85$

$f(3)=2(27)-24(3)+107=54-72+107=89$

Hence, the absolute maximum value of $f(x)$ in the interval $[1,3]$ is 89 occurring at $x=$ 3.

Next, we consider the interval $[-3,-1]$.

Evaluate the value of $f$ at the critical point $x=-2 \square[-3,-1]$ and at the end points of the interval $[1,3]$.

$f(-3)=2(-27)-24(-3)+107=-54+72+107=125$

$f(-1)=2(-1)-24(-1)+107=-2+24+107=129$

$f(-2)=2(-8)-24(-2)+107=-16+48+107=139$

Hence, the absolute maximum value of $f(x)$ in the interval $[-3,-1]$ is 139 occurring at $x$ $=-2$.

11. It is given that at $x=1$, the function $x^{4}-62 x^{2}+a x+9$ attains its maximum value, on the interval $[0,2]$. Find the value of $a$.

Solution

Let $f(x)=x^{4}-62 x^{2}+a x+9$.

$\therefore f^{\prime}(x)=4 x^{3}-124 x+a$

It is given that function $f$ attains its maximum value on the interval $[0,2]$ at $x=1$.

$\therefore f^{\prime}(1)=0$

$\Rightarrow 4-124+a=0$

$\Rightarrow a=120$

Hence, the value of $a$ is 120 .

12. Find the maximum and minimum values of $x+\sin 2 x$ on $[0,2 \pi]$.

Solution

Let $f(x)=x+\sin 2 x$.

$\therefore f^{\prime}(x)=1+2 \cos 2 x$

Now, $f^{\prime}(x)=0 \Rightarrow \cos 2 x=-\frac{1}{2}=-\cos \frac{\pi}{3}=\cos (\pi-\frac{\pi}{3})=\cos \frac{2 \pi}{3}$

$2 x=2 \pi \pm \frac{2 \pi}{3} \quad n \in \mathbf{Z}$

$\Rightarrow x=n \pi \pm \frac{\pi}{3}, n \in \mathbf{Z}$

$\Rightarrow x=\frac{\pi}{3}, \frac{2 \pi}{3}, \frac{4 \pi}{3}, \frac{5 \pi}{3} \in[0,2 \pi]$

Then, we evaluate the value of $f$ at critical points $x=\frac{\pi}{3}, \frac{2 \pi}{3}, \frac{4 \pi}{3}, \frac{5 \pi}{3}$ and at the end points of the interval $[0,2 \pi]$. $f(\frac{\pi}{3})=\frac{\pi}{3}+\sin \frac{2 \pi}{3}=\frac{\pi}{3}+\frac{\sqrt{3}}{2}$

$f(\frac{2 \pi}{3})=\frac{2 \pi}{3}+\sin \frac{4 \pi}{3}=\frac{2 \pi}{3}-\frac{\sqrt{3}}{2}$

$f(\frac{4 \pi}{3})=\frac{4 \pi}{3}+\sin \frac{8 \pi}{3}=\frac{4 \pi}{3}+\frac{\sqrt{3}}{2}$

$f(\frac{5 \pi}{3})=\frac{5 \pi}{3}+\sin \frac{10 \pi}{3}=\frac{5 \pi}{3}-\frac{\sqrt{3}}{2}$

$f(0)=0+\sin 0=0$

$f(2 \pi)=2 \pi+\sin 4 \pi=2 \pi+0=2 \pi$

Hence, we can conclude that the absolute maximum value of $f(x)$ in the interval $[0,2 \pi]$ is $2 \pi$ occurring at $x=2 \pi$ and the absolute minimum value of $f(x)$ in the interval $[0,2 \pi]$ is 0 occurring at $x=0$.

13. Find two numbers whose sum is 24 and whose product is as large as possible.

Solution

Let one number be $x$. Then, the other number is $(24-x)$.

Let $P(x)$ denote the product of the two numbers. Thus, we have:

$ \begin{aligned} & P(x)=x(24-x)=24 x-x^{2} \\ & \therefore P^{\prime}(x)=24-2 x \\ & P^{\prime \prime}(x)=-2 \end{aligned} $

Now,

$P^{\prime}(x)=0 \Rightarrow x=12$

Also,

$P^{\prime \prime}(12)=-2<0$

$\square$ By second derivative test, $x=12$ is the point of local maxima of $P$. Hence, the product of the numbers is the maximum when the numbers are 12 and $24-12=12$.

14. Find two positive numbers $x$ and $y$ such that $x+y=60$ and $x y^{3}$ is maximum.

Solution

The two numbers are $x$ and $y$ such that $x+y=60$.

$\square y=60-x$

Let $f(x)=x y^{3}$.

$\Rightarrow f(x)=x(60-x)^{3}$

$\therefore f^{\prime}(x)=(60-x)^{3}-3 x(60-x)^{2}$

$=(60-x)^{2}[60-x-3 x]$

$=(60-x)^{2}(60-4 x)$

And, $f^{\prime \prime}(x)=-2(60-x)(60-4 x)-4(60-x)^{2}$

$ \begin{aligned} & =-2(60-x)[60-4 x+2(60-x)] \\ & =-2(60-x)(180-6 x) \\ & =-12(60-x)(30-x) \end{aligned} $

Now, $f^{\prime}(x)=0 \Rightarrow x=60$ or $x=15$

When $x=60, f^{\prime \prime}(x)=0$.

When $x=15, f^{\prime \prime}(x)=-12(60-15)(30-15)=-12 \times 45 \times 15<0$.

$\square$ By second derivative test, $x=15$ is a point of local maxima of $f$. Thus, function $x y^{3}$ is maximum when $x=15$ and $y=60-15=45$.

Hence, the required numbers are 15 and 45 .

15. Find two positive numbers $x$ and $y$ such that their sum is 35 and the product $x^{2} y^{5}$ is a maximum.

Solution

Let one number be $x$. Then, the other number is $y=(35-x)$.

Let $P(x)=x^{2} y^{5}$. Then, we have:

$ \begin{aligned} & P(x)=x^{2}(35-x)^{5} \\ & \begin{aligned} \therefore P^{\prime}(x) & =2 x(35-x)^{5}-5 x^{2}(35-x)^{4} \\ & =x(35-x)^{4}[2(35-x)-5 x] \\ & =x(35-x)^{4}(70-7 x) \\ & =7 x(35-x)^{4}(10-x) \end{aligned} \end{aligned} $

And, $P^{\prime \prime}(x)=7(35-x)^{4}(10-x)+7 x[-(35-x)^{4}-4(35-x)^{3}(10-x)]$

$ \begin{aligned} & =7(35-x)^{4}(10-x)-7 x(35-x)^{4}-28 x(35-x)^{3}(10-x) \\ & =7(35-x)^{3}[(35-x)(10-x)-x(35-x)-4 x(10-x)] \\ & =7(35-x)^{3}[350-45 x+x^{2}-35 x+x^{2}-40 x+4 x^{2}] \\ & =7(35-x)^{3}(6 x^{2}-120 x+350) \end{aligned} $

Now, $P^{\prime}(x)=0 \Rightarrow x=0, x=35, x=10$

When $x=35,{ }^{\prime}(x)=f(x)=0$ and $y=35-35=0$. This will make the product $x^{2} y^{5}$ equal to 0 .

When $x=0, y=35-0=35$ and the product $x^{2} y^{2}$ will be 0 .

$\square x=0$ and $x=35$ cannot be the possible values of $x$.

When $x=10$, we have:

$ \begin{aligned} P^{\prime \prime}(x) & =7(35-10)^{3}(6 \times 100-120 \times 10+350) \\ & =7(25)^{3}(-250)<0 \end{aligned} $

$\square$ By second derivative test, $P(x)$ will be the maximum when $x=10$ and $y=35-10=$ 25.

Hence, the required numbers are 10 and 25 .

16. Find two positive numbers whose sum is 16 and the sum of whose cubes is minimum.

Solution

Let one number be $x$. Then, the other number is $(16-x)$.

Let the sum of the cubes of these numbers be denoted by $S(x)$. Then,

$S(x)=x^{3}+(16-x)^{3}$

$\therefore S^{\prime}(x)=3 x^{2}-3(16-x)^{2}, S^{\prime \prime}(x)=6 x+6(16-x)$

Now, $S^{\prime}(x)=0 \Rightarrow 3 x^{2}-3(16-x)^{2}=0$

$\Rightarrow x^{2}-(16-x)^{2}=0$

$\Rightarrow x^{2}-256-x^{2}+32 x=0$

$\Rightarrow x=\frac{256}{32}=8$

Now, $S^{\prime \prime}(8)=6(8)+6(16-8)=48+48=96>0$

$\square$ By second derivative test, $x=8$ is the point of local minima of $S$.

Hence, the sum of the cubes of the numbers is the minimum when the numbers are 8 and $16-8=8$.

17. A square piece of tin of side $18 cm$ is to be made into a box without top, by cutting a square from each corner and folding up the flaps to form the box. What should be the side of the square to be cut off so that the volume of the box is the maximum possible.

Solution

Let the side of the square to be cut off be $x cm$. Then, the length and the breadth of the box will be $(18-2 x) cm$ each and the height of the box is $x cm$.

Therefore, the volume $V(x)$ of the box is given by,

$V(x)=x(18-2 x)^{2}$ $\therefore V^{\prime}(x)=(18-2 x)^{2}-4 x(18-2 x)$

$=(18-2 x)[18-2 x-4 x]$

$=(18-2 x)(18-6 x)$

$=6 \times 2(9-x)(3-x)$

$=12(9-x)(3-x)$

And, $V^{\prime \prime}(x)=12[-(9-x)-(3-x)]$

$=-12(9-x+3-x)$

$=-12(12-2 x)$

$=-24(6-x)$

Now, $V^{\prime}(x)=0 \Rightarrow x=9$ or $x=3$

If $x=9$, then the length and the breadth will become 0 .

$\therefore x \neq 9$.

$\Rightarrow x=3$.

Now, $V^{\prime \prime}(3)=-24(6-3)=-72<0$

$\therefore$ By second derivative test, $x=3$ is the point of maxima of $V$.

Hence, if we remove a square of side $3 cm$ from each corner of the square tin and make a box from the remaining sheet, then the volume of the box obtained is the largest possible.

18. A rectangular sheet of tin $45 cm$ by $24 cm$ is to be made into a box without top, by cutting off square from each corner and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is maximum?

Solution

Let the side of the square to be cut off be $x cm$. Then, the height of the box is $x$, the length is $45-2 x$, and the breadth is $24-2 x$.

Therefore, the volume $V(x)$ of the box is given by,

$ \begin{aligned} V(x) & =x(45-2 x)(24-2 x) \\ & =x(1080-90 x-48 x+4 x^{2}) \\ & =4 x^{3}-138 x^{2}+1080 x \end{aligned} $

$\therefore V^{\prime}(x)=12 x^{2}-276 x+1080$

$ =12(x^{2}-23 x+90) $

$ =12(x-18)(x-5) $

$V^{\prime \prime}(x)=24 x-276=12(2 x-23)$

Now, ${ }^{V^{\prime}}(x)=0 \Rightarrow x=18$ and $x=5$

It is not possible to cut off a square of side $18 cm$ from each corner of the rectangular sheet. Thus, $x$ cannot be equal to 18 .

$\square x=5$

Now, $V^{\prime \prime}(5)=12(10-23)=12(-13)=-156<0$

$\therefore$ By second derivative test, $x=5$ is the point of maxima.

Hence, the side of the square to be cut off to make the volume of the box maximum possible is $5 cm$.

19. Show that of all the rectangles inscribed in a given fixed circle, the square has the maximum area.

Solution

Let a rectangle of length / and breadth $b$ be inscribed in the given circle of radius $a$. Then, the diagonal passes through the centre and is of length $2 a cm$.

Now, by applying the Pythagoras theorem, we have:

$ \begin{aligned} & (2 a)^{2}=l^{2}+b^{2} \\ & \Rightarrow b^{2}=4 a^{2}-l^{2} \\ & \Rightarrow b=\sqrt{4 a^{2}-l^{2}} \end{aligned} $

$\square$ Area of the rectangle, $A=l \sqrt{4 a^{2}-l^{2}}$

$\therefore \frac{d A}{d l}=\sqrt{4 a^{2}-l^{2}}+l \frac{1}{2 \sqrt{4 a^{2}-l^{2}}}(-2 l)=\sqrt{4 a^{2}-l^{2}}-\frac{l^{2}}{\sqrt{4 a^{2}-l^{2}}}$

$ =\frac{4 a^{2}-2 l^{2}}{\sqrt{4 a^{2}-l^{2}}} $

$\frac{d^{2} A}{d l^{2}}=\frac{\sqrt{4 a^{2}-l^{2}}(-4 l)-(4 a^{2}-2 l^{2}) \frac{(-2 l)}{2 \sqrt{4 a^{2}-l^{2}}}}{(4 a^{2}-l^{2})}$

$ =\frac{(4 a^{2}-l^{2})(-4 l)+l(4 a^{2}-2 l^{2})}{(4 a^{2}-l^{2})^{\frac{3}{2}}} $

$ =\frac{-12 a^{2} l+2 l^{3}}{(4 a^{2}-l^{2})^{\frac{3}{2}}}=\frac{-2 l(6 a^{2}-l^{2})}{(4 a^{2}-l^{2})^{\frac{3}{2}}} $

Now, $\frac{d A}{d l}=0$ gives $4 a^{2}=2 l^{2} \Rightarrow l=\sqrt{2} a$

$ \Rightarrow b=\sqrt{4 a^{2}-2 a^{2}}=\sqrt{2 a^{2}}=\sqrt{2} a $

Now, when $l=\sqrt{2} a$,

$\frac{d^{2} A}{d l^{2}}=\frac{-2(\sqrt{2} a)(6 a^{2}-2 a^{2})}{2 \sqrt{2} a^{3}}=\frac{-8 \sqrt{2} a^{3}}{2 \sqrt{2} a^{3}}=-4<0$

$\therefore$ By the second derivative test, when $l=\sqrt{2} a$, then the area of the rectangle is the maximum.

Since $l=b=\sqrt{2} a$, the rectangle is a square.

Hence, it has been proved that of all the rectangles inscribed in the given fixed circle, the square has the maximum area.

20. Show that the right circular cylinder of given surface and maximum volume is such that its height is equal to the diameter of the base.

Solution

Let $r$ and $h$ be the radius and height of the cylinder respectively.

Then, the surface area $(S)$ of the cylinder is given by,

$ \begin{aligned} & S=2 \pi r^{2}+2 \pi r h \\ & \Rightarrow h=\frac{S-2 \pi r^{2}}{2 \pi r} \\ &=\frac{S}{2 \pi}(\frac{1}{r})-r \end{aligned} $

Let $V$ be the volume of the cylinder. Then,

$V=\pi r^{2} h=\pi r^{2}[\frac{S}{2 \pi}(\frac{1}{r})-r]=\frac{S r}{2}-\pi r^{3}$

Then, $\frac{d V}{d r}=\frac{S}{2}-3 \pi r^{2}, \frac{d^{2} V}{d r^{2}}=-6 \pi r$

Now, $\frac{d V}{d r}=0 \Rightarrow \frac{S}{2}=3 \pi r^{2} \Rightarrow r^{2}=\frac{S}{6 \pi}$

When $r^{2}=\frac{S}{6 \pi}$, then $\frac{d^{2} V}{d r^{2}}=-6 \pi(\sqrt{\frac{S}{6 \pi}})<0$.

By second derivative test, the volume is the maximum when $r^{2}=\frac{S}{6 \pi}$.

Now, when $r^{2}=\frac{S}{6 \pi}$, then $h=\frac{6 \pi r^{2}}{2 \pi}(\frac{1}{r})-r=3 r-r=2 r$.

Hence, the volume is the maximum when the height is twice the radius i.e., when the height is equal to the diameter.

21. Of all the closed cylindrical cans (right circular), of a given volume of 100 cubic centimetres, find the dimensions of the can which has the minimum surface area?

Solution

Let $r$ and $h$ be the radius and height of the cylinder respectively.

Then, volume $(V)$ of the cylinder is given by,

$V=\pi r^{2} h=100 \quad$ (given)

$\therefore h=\frac{100}{\pi r^{2}}$

Surface area $(S$ ) of the cylinder is given by,

$S=2 \pi r^{2}+2 \pi r h=2 \pi r^{2}+\frac{200}{r}$

$\therefore \frac{d S}{d r}=4 \pi r-\frac{200}{r^{2}}, \frac{d^{2} S}{d r^{2}}=4 \pi+\frac{400}{r^{3}}$

$\frac{d S}{d r}=0 \Rightarrow 4 \pi r=\frac{200}{r^{2}}$

$\Rightarrow r^{3}=\frac{200}{4 \pi}=\frac{50}{\pi}$

$\Rightarrow r=(\frac{50}{\pi})^{\frac{1}{3}}$

Now, it is observed that when $r=(\frac{50}{\pi})^{\frac{1}{3}}, \frac{d^{2} S}{d r^{2}}>0$.

$\square$ By second derivative test, the surface area is the minimum when the radius of the

cylinder is $(\frac{50}{\pi})^{\frac{1}{3}} cm$.

When $r=(\frac{50}{\pi})^{\frac{1}{3}}, h=\frac{100}{\pi(\frac{50}{\pi})^{\frac{2}{3}}}=\frac{2 \times 50}{(50)^{\frac{2}{3}}()^{1-\frac{2}{3}}}=2(\frac{50}{\pi})^{\frac{1}{3}} cm$.

Hence, the required dimensions of the can which has the minimum surface area is given

by radius $=(\frac{50}{\pi})^{\frac{1}{3}} cm$ and height $=2(\frac{50}{\pi})^{\frac{1}{3}} cm$.

22. A wire of length $28 m$ is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the square and the circle is minimum?

Solution

Let a piece of length / be cut from the given wire to make a square.

Then, the other piece of wire to be made into a circle is of length $(28-I) m$.

Now, side of square $=\frac{l}{4}$.

Let $r$ be the radius of the circle. Then,

$ 2 \pi r=28-l \Rightarrow r=\frac{1}{2 \pi}(28-l) \text{. } $

The combined areas of the square and the circle $(A)$ is given by,

$A=(\text{ side of the square })^{2}+r^{2}$

$=\frac{l^{2}}{16}+\pi[\frac{1}{2 \pi}(28-l)]^{2}$

$=\frac{l^{2}}{16}+\frac{1}{4 \pi}(28-l)^{2}$

$\therefore \frac{d A}{d l}=\frac{2 l}{16}+\frac{2}{4 \pi}(28-l)(-1)=\frac{l}{8}-\frac{1}{2 \pi}(28-l)$

$\frac{d^{2} A}{d l^{2}}=\frac{1}{8}+\frac{1}{2 \pi}>0$

Now, $\frac{d A}{d l}=0 \Rightarrow \frac{l}{8}-\frac{1}{2 \pi}(28-l)=0$

$\Rightarrow \frac{\pi l-4(28-l)}{8 \pi}=0$

$\Rightarrow(\pi+4) l-112=0$

$\Rightarrow l=\frac{112}{\pi+4}$

Thus, when $l=\frac{112}{\pi+4}, \frac{d^{2} A}{d l^{2}}>0$.

$\therefore$ By second derivative test, the area $(A)$ is the minimum when $l=\frac{112}{\pi+4}$.

Hence, the combined area is the minimum when the length of the wire in making the

square is $\frac{112}{\pi+4} cm$ while the length of the wire in making the circle

is $28-\frac{112}{\pi+4}=\frac{28 \pi}{\pi+4} cm$.

23. Prove that the volume of the largest cone that can be inscribed in a sphere of radius $R$ is $\frac{8}{27}$ of the volume of the sphere.

Solution

Let $r$ and $h$ be the radius and height of the cone respectively inscribed in a sphere of radius $R$.

Let $V$ be the volume of the cone.

Then, $V=\frac{1}{3} \pi r^{2} h$

Height of the cone is given by,

$h=R+AB=R+\sqrt{R^{2}-r^{2}} \quad$ [ $ABC$ is a right triangle]

$ \begin{aligned} & \therefore V=\frac{1}{3} \pi r^{2}(R+\sqrt{R^{2}-r^{2}}) \\ & =\frac{1}{3} \pi r^{2} R+\frac{1}{3} \pi r^{2} \sqrt{R^{2}-r^{2}} \\ & \therefore \frac{d V}{d r}=\frac{2}{3} \pi r R+\frac{2}{3} \pi r \sqrt{R^{2}-r^{2}}+\frac{1}{3} \pi r^{2} \cdot \frac{(-2 r)}{2 \sqrt{R^{2}-r^{2}}} \\ & =\frac{2}{3} \pi r R+\frac{2}{3} \pi r \sqrt{R^{2}-r^{2}}-\frac{1}{3} \pi \frac{r^{3}}{\sqrt{R^{2}-r^{2}}} \\ & =\frac{2}{3} \pi r R+\frac{2 \pi r(R^{2}-r^{2})-\pi r^{3}}{3 \sqrt{R^{2}-r^{2}}} \\ & =\frac{2}{3} \pi r R+\frac{2 \pi r R^{2}-3 \pi r^{3}}{3 \sqrt{R^{2}-r^{2}}} \\ & \frac{d^{2} V}{d r^{2}}=\frac{2 \pi R}{3}+\frac{3 \sqrt{R^{2}-r^{2}}(2 \pi R^{2}-9 \pi r^{2})-(2 \pi r R^{2}-3 \pi r^{3}) \cdot \frac{(-2 r)}{6 \sqrt{R^{2}-r^{2}}}}{9(R^{2}-r^{2})} \\ & =\frac{2}{3} \pi R+\frac{9(R^{2}-r^{2})(2 \pi R^{2}-9 \pi r^{2})+2 \pi r^{2} R^{2}+3 \pi r^{4}}{27(R^{2}-r^{2})^{\frac{3}{2}}} \end{aligned} $

Now, $\frac{d V}{d r}=0 \Rightarrow \frac{2}{3} \quad r R=\frac{3 \pi r^{3}-2 \pi r R^{2}}{3 \sqrt{R^{2}-r^{2}}}$

$\Rightarrow 2 R=\frac{3 r^{2}-2 R^{2}}{\sqrt{R^{2}-r^{2}}} \Rightarrow 2 R \sqrt{R^{2}-r^{2}}=3 r^{2}-2 R^{2}$

$\Rightarrow 4 R^{2}(R^{2}-r^{2})=(3 r^{2}-2 R^{2})^{2}$

$\Rightarrow 4 R^{4}-4 R^{2} r^{2}=9 r^{4}+4 R^{4}-12 r^{2} R^{2}$

$\Rightarrow 9 r^{4}=8 R^{2} r^{2}$

$\Rightarrow r^{2}=\frac{8}{9} R^{2}$

When $r^{2}=\frac{8}{9} R^{2}$, then $\frac{d^{2} V}{d r^{2}}<0$.

By second derivative test, the volume of the cone is the maximum when $r^{2}=\frac{8}{9} R^{2}$.

When $r^{2}=\frac{8}{9} R^{2}, h=R+\sqrt{R^{2}-\frac{8}{9} R^{2}}=R+\sqrt{\frac{1}{9} R^{2}}=R+\frac{R}{3}=\frac{4}{3} R$.

Therefore,

$=\frac{1}{3} \pi(\frac{8}{9} R^{2})(\frac{4}{3} R)$

$=\frac{8}{27}(\frac{4}{3} \pi R^{3})$

$=\frac{8}{27} \times($ Volume of the sphere $)$

Hence, the volume of the largest cone that can be inscribed in the sphere is $\frac{8}{27}$ the volume of the sphere.

24. Show that the right circular cone of least curved surface and given volume has an altitude equal to $\sqrt{2}$ time the radius of the base.

Solution

Let $r$ and $h$ be the radius and the height (altitude) of the cone respectively.

Then, the volume $(V)$ of the cone is given as:

$V=\frac{1}{3} \pi r^{2} h \Rightarrow h=\frac{3 V}{r^{2}}$

The surface area $(S)$ of the cone is given by,

$S=\pi r l$ (where $/$ is the slant height)

$=\pi r \sqrt{r^{2}+h^{2}}$

$=\pi r \sqrt{r^{2}+\frac{9 \hbar^{2}}{\pi^{2} r^{4}}} \stackrel{\pi}{=} \frac{r \sqrt{9^{2} r^{6}+V^{2}}}{\pi r^{2}}$

$=\frac{1}{r} \sqrt{\pi^{2} r^{6}+9 V^{2}}$

$ \begin{aligned} \therefore \frac{d S}{d r} & =\frac{r \cdot \frac{6 \pi^{2} r^{5}}{2 \sqrt{{ }^{2} r^{6} 9 V^{2}}}-\sqrt{\pi^{2} r^{6}+9 V^{2}}}{r^{2}} \\ & =\frac{3 \pi^{2} r^{6}-\pi^{2} r^{6}-9 V^{2}}{r^{2} \sqrt{\pi^{2} r^{6}+9 V^{2}}} \\ & =\frac{2 \pi^{2} r^{6}-9 V^{2}}{r^{2} \sqrt{\pi^{2} r^{6}+9 V^{2}}} \\ & =\frac{2 \pi^{2} r^{6}-9 V^{2}}{r^{2} \sqrt{\pi^{2} r^{6}+9 V^{2}}} \end{aligned} $

Now, $\frac{d S}{d r}=0 \Rightarrow 2 \pi^{2} r^{6}=9 V^{2} \Rightarrow r^{6}=\frac{9 V^{2}}{2 \pi^{2}}$

Thus, it can be easily verified that when $r^{6}=\frac{9 V^{2}}{2 \pi^{2}}, \frac{d^{2} S}{d r^{2}}>0$.

$\square$ By second derivative test, the surface area of the cone is the least when $r^{6}=\frac{9 V^{2}}{2 \pi^{2}}$.

When $r^{6}=\frac{9 V^{2}}{2 \pi^{2}}, h=\frac{3 V}{\pi r^{2}}=\frac{3}{\pi r^{2}}(\frac{2 \pi^{2} r^{6}}{9})^{\frac{1}{2}}=\frac{3}{\pi r^{2}} \cdot \frac{\sqrt{2} \pi r^{3}}{3}=\sqrt{2} r$.

Hence, for a given volume, the right circular cone of the least curved surface has an altitude equal to $\sqrt{2}$ times the radius of the base.

25. Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is $\tan ^{-1} \sqrt{2}$.

Solution

Let $\theta$ be the semi-vertical angle of the cone.

It is clear that

$ \theta \in[0, \frac{\pi}{2}] $

Let $r, h$, and $/$ be the radius, height, and the slant height of the cone respectively. The slant height of the cone is given as constant.

Now, $r=I \sin \theta$ and $h=I \cos \theta$

The volume $(V)$ of the cone is given by,

$ \begin{aligned} & V=\frac{1}{3} \pi r^{2} h \\ & =\frac{1}{3} \pi(l^{2} \sin ^{2} \theta)(l \cos \theta) \\ & =\frac{1}{3} \pi l^{3} \sin ^{2} \theta \cos \theta \\ & \begin{aligned} \therefore \frac{d V}{d \theta} & =\frac{l^{3} \pi}{3}[\sin ^{2} \theta(-\sin \theta)+\cos \theta(2 \sin \theta \cos \theta)] \\ & =\frac{l^{3} \pi}{3}[-\sin ^{3}+2 \sin \theta \cos ^{2} \theta] \end{aligned} \\ & \begin{aligned} \frac{d^{2} V}{d \theta^{2}} & =\frac{l^{3} \pi}{3}[-3 \sin ^{2} \theta \cos \theta+2 \cos ^{3} \theta-4 \sin ^{2} \theta \cos \theta] \\ & =\frac{l^{3} \pi}{3}[2 \cos ^{3} \theta-7 \sin ^{2} \theta \cos \theta] \end{aligned} \end{aligned} $

Now, $\frac{d V}{d \theta}=0$

$\Rightarrow \sin ^{3} \theta=2 \sin \theta \cos ^{2} \theta$

$\Rightarrow \tan ^{2} \theta=2$

$\Rightarrow \tan \theta=\sqrt{2}$

$\Rightarrow \theta=\tan ^{-1} \sqrt{2}$

Now, when $\theta=\tan ^{-1} \sqrt{2}$, then $\tan ^{2} \theta=2$ or $\sin ^{2} \theta=2 \cos ^{2} \theta$.

Then, we have:

$\frac{d^{2} V}{d \theta^{2}}=\frac{l^{3} \pi}{3}[2 \cos ^{3} \theta-14 \cos ^{3} \theta]=-4 \pi l^{3} \cos ^{3} \theta<0$ for $\theta \in[0, \frac{\pi}{2}]$

$\square$ By second derivative test, the volume $(V)$ is the maximum when $\theta=\tan ^{-1} \sqrt{2}$.

Hence, for a given slant height, the semi-vertical angle of the cone of the maximum volume is $\tan ^{-1} \sqrt{2}$.

26. Show that semi-vertical angle of right circular cone of given surface area and maximum volume is $\sin ^{-1} \frac{1}{3}$.

Solution

Let $\mathrm{r}, \mathrm{h}, \mathrm{l}$ be the radius, height and slant height of the right circular cone respectively. Let $S$ be the given surface area of the cone. We have, $l^2=\mathrm{r}^2+\mathrm{h}^2 \ldots .(1)$

$\begin{aligned} & S=\pi r l+\pi r^2 \ & S-\pi r^2=\pi r l \ & \Rightarrow l=\frac{S-\pi r^2}{\pi r} \ldots . . \end{aligned}$

$\begin{aligned} & \mathrm{V}=\frac{1}{3} \pi \mathrm{r}^2 \mathrm{~h} \\ & \Rightarrow \mathrm{V}=\frac{1}{3} \pi \mathrm{r}^2 \sqrt{1^2-\mathrm{r}^2}(\mathrm{by}(1)) \\ & \Rightarrow \mathrm{V}^2=\frac{1}{9} \pi^2 \mathrm{r}^4\left(\mathrm{l}^2-\mathrm{r}^2\right) \end{aligned}$

$\begin{aligned} & \Rightarrow \mathrm{V}^2=\frac{1}{9} \pi^2 \mathrm{r}^4\left[\left(\frac{\mathrm{S}-\pi \mathrm{r}^2}{\pi \mathrm{r}}\right)^2-\mathrm{r}^2\right] \\ & \Rightarrow \mathrm{V}^2=\frac{1}{9} \pi^2 \mathrm{r}^4\left[\frac{\left(\mathrm{S}-\pi \mathrm{r}^2\right)^2-\pi^2 \mathrm{r}^4}{\pi^2 \mathrm{r}^2}\right] \\ & \Rightarrow \mathrm{V}^2=\frac{1}{9} \mathrm{r}^2\left[\left(\mathrm{~S}-\pi \mathrm{r}^2\right)^2-\pi^2 \mathrm{r}^4\right] \\ & \Rightarrow \mathrm{V}^2=\frac{1}{9} \mathrm{r}^2\left[\mathrm{~S}^2-2 \pi \mathrm{Sr}^2+\pi^2 \mathrm{r}^4-\pi^2 \mathrm{r}^4\right] \\ & \Rightarrow \mathrm{V}^2=\frac{1}{9}\left(\mathrm{r}^2 \mathrm{~S}^2-2 \pi \mathrm{Sr}^4\right) \\ \end{aligned}$

$2 \mathrm{~V} \frac{\mathrm{dV}}{\mathrm{dr}}=\frac{\mathrm{S}^2}{9} 2 \mathrm{r}-\frac{2 \pi \mathrm{S}}{9} 4 \mathrm{r}^3$

$2 \mathrm{~V} \frac{\mathrm{dV}}{\mathrm{dr}}=\frac{2 \mathrm{rS}}{9}\left(\mathrm{~S}-4 \pi \mathrm{r}^2\right)$

For maximum volume, $\frac{\mathrm{dV}}{\mathrm{dr}}=0$

$\begin{aligned} & \Rightarrow \frac{2 \mathrm{rS}}{9}\left(\mathrm{~S}-4 \pi \mathrm{r}^2\right)=0 \\ & \Rightarrow \mathrm{r}=\mathrm{o} \text { or } \mathrm{S}-4 \pi \mathrm{r}^2=0 \end{aligned}$

Since, $r$ cannot be $o$

$\begin{aligned} & \Rightarrow \mathrm{S}=4 \pi \mathrm{r}^2 \ & \Rightarrow \mathrm{r}^2=\frac{\mathrm{S}}{4 \pi} \ & \Rightarrow \mathrm{r}^2=\frac{\pi \mathrm{rl}+\pi \mathrm{r}^2}{4 \pi} \end{aligned}$

$\begin{aligned} & \Rightarrow 4 \pi r^2=\pi r l+\pi r^2 \ & \Rightarrow 3 \pi r^2=\pi r l \ & \Rightarrow l=3 r \end{aligned}$

Let $\alpha$ be the semi-vertical angle.

$\begin{aligned} & \sin \alpha=\frac{r}{l} \\ & \sin \alpha=\frac{r}{3 r} \\ & \Rightarrow \alpha=\sin ^{-1}\left(\frac{1}{3}\right) \end{aligned}$

Choose the correct answer in Questions 27 and 29.

27. The point on the curve $x^{2}=2 y$ which is nearest to the point $(0,5)$ is

(A) $(2 \sqrt{2}, 4)$

(B) $(2 \sqrt{2}, 0)$

(C) $(0,0)$

(D) $(2,2)$

Solution

The given curve is $x^{2}=2 y$.

For each value of $x$, the position of the point will be $(x, \frac{x^{2}}{2})$.

The distance $d(x)$ between the points $(x, \frac{x^{2}}{2})$ and $(0,5)$ is given by,

$d(x)=\sqrt{(x-0)^{2}+(\frac{x^{2}}{2}-5)^{2}}=\sqrt{x^{2}+\frac{x^{4}}{4}+25-5 x^{2}}=\sqrt{\frac{x^{4}}{4}-4 x^{2}+25}$

$\therefore d^{\prime}(x)=\frac{(x^{3}-8 x)}{2 \sqrt{\frac{x^{4}}{4}-4 x^{2}+25}}=\frac{(x^{3}-8 x)}{\sqrt{x^{4}-16 x^{2}+100}}$

Now, $d^{\prime}(x)=0 \Rightarrow x^{3}-8 x=0$

$\Rightarrow x(x^{2}-8)=0$

$\Rightarrow x=0, \pm 2 \sqrt{2}$

$ \begin{aligned} & \begin{aligned} & \text{ And, } d^{\prime \prime}(x)= \frac{\sqrt{x^{4}-16 x^{2}+100}(3 x^{2}-8)-(x^{3}-8 x) \cdot \frac{4 x^{3}-32 x}{2 \sqrt{x^{4}-16 x^{2}+100}}}{(x^{4}-16 x^{2}+100)} \\ &=\frac{(x^{4}-16 x^{2}+100)(3 x^{2}-8)-2(x^{3}-8 x)(x^{3}-8 x)}{(x^{4}-16 x^{2}+100)^{\frac{3}{2}}} \\ &=\frac{(x^{4}-16 x^{2}+100)(3 x^{2}-8)-2(x^{3}-8 x)^{2}}{(x^{4}-16 x^{2}+100)^{\frac{3}{2}}} \\ & \text{ When, } x=0 \text{, then } d^{\prime \prime}(x)=\frac{36(-8)}{6^{3}}<0 . \end{aligned} \\ & \text{ When, } x= \pm 2 \sqrt{2}, d^{\prime \prime}(x)>0 . \end{aligned} $

$\square$ By second derivative test, $d(x)$ is the minimum at $x= \pm 2 \sqrt{2}$.

When $x= \pm 2 \sqrt{2}, y=\frac{(2 \sqrt{2})^{2}}{2}=4$.

Hence, the point on the curve $x^{2}=2 y$ which is nearest to the point $(0,5)$ is $( \pm 2 \sqrt{2}, 4)$. The correct answer is $A$.

28. For all real values of $x$, the minimum value of $\frac{1-x+x^{2}}{1+x+x^{2}}$ is

(A) 0

(B) 1

(C) 3

(D) $\frac{1}{3}$

Solution

Let $f(x)=\frac{1-x+x^{2}}{1+x+x^{2}}$.

$ \begin{aligned} \therefore f^{\prime}(x) & =\frac{(1+x+x^{2})(-1+2 x)-(1-x+x^{2})(1+2 x)}{(1+x+x^{2})^{2}} \\ & =\frac{-1+2 x-x+2 x^{2}-x^{2}+2 x^{3}-1-2 x+x+2 x^{2}-x^{2}-2 x^{3}}{(1+x+x^{2})^{2}} \\ & =\frac{2 x^{2}-2}{(1+x+x^{2})^{2}}=\frac{2(x^{2}-1)}{(1+x+x^{2})^{2}} \end{aligned} $

$\therefore f^{\prime}(x)=0 \Rightarrow x^{2}=1 \Rightarrow x= \pm 1$

Now, $f^{\prime \prime}(x)=\frac{2[(1+x+x^{2})^{2}(2 x)-(x^{2}-1)(2)(1+x+x^{2})(1+2 x)]}{(1+x+x^{2})^{4}}$

$ =\frac{4(1+x+x^{2})[(1+x+x^{2}) x-(x^{2}-1)(1+2 x)]}{(1+x+x^{2})^{4}} $

$ \begin{aligned} & =\frac{4[x+x^{2}+x^{3}-x^{2}-2 x^{3}+1+2 x]}{(1+x+x^{2})^{3}} \\ & =\frac{4(1+3 x-x^{3})}{(1+x+x^{2})^{3}} \end{aligned} $

And, $f^{\prime \prime}(1)=\frac{4(1+3-1)}{(1+1+1)^{3}}=\frac{4(3)}{(3)^{3}}=\frac{4}{9}>0$

Also, $f^{\prime \prime}(-1)=\frac{4(1-3+1)}{(1-1+1)^{3}}=4(-1)=-4<0$

$\square$ By second derivative test, $f$ is the minimum at $x=1$ and the minimum value is given

by $f(1)=\frac{1-1+1}{1+1+1}=\frac{1}{3}$.

The correct answer is $D$.

29. The maximum value of $[x(x-1)+1]^{\frac{1}{3}}, 0 \leq x \leq 1$ is

(A) $\frac{1}{3} \frac{1}{3}$

(B) $\frac{1}{2}$

(C) 1

(D) 0

Solution

Let $f(x)=[x(x-1)+1]^{\frac{1}{3}}$.

$\therefore f^{\prime}(x)=\frac{2 x-1}{3[x(x-1)+1]^{\frac{2}{3}}}$

Now, $f^{\prime}(x)=0 \Rightarrow x=\frac{1}{2}$

Then, we evaluate the value of $f$ at critical point $x=\frac{1}{2}$ and at the end points of the interval $[0,1]$ {i.e., at $x=0$ and $x=1}$.

$f(0)=[0(0-1)+1]^{\frac{1}{3}}=1$

$f(1)=[1(1-1)+1]^{\frac{1}{3}}=1$

$f(\frac{1}{2})=[\frac{1}{2}(\frac{-1}{2})+1]^{\frac{1}{3}}=(\frac{3}{4})^{\frac{1}{3}}$

Hence, we can conclude that the maximum value of $f$ in the interval $[0,1]$ is 1 .

The correct answer is $C$.

Miscellaneous Examples

Example 30 A car starts from a point $P$ at time $t=0$ seconds and stops at point $Q$. The distance $x$, in metres, covered by it, in $t$ seconds is given by

$ x=t^{2} \quad 2-\frac{t}{3} $

Find the time taken by it to reach $Q$ and also find distance between $P$ and $Q$.

Solution Let $v$ be the velocity of the car at $t$ seconds.

Now

$ x=t^{2}(2-\frac{t}{3}) $

Therefore

$ v=\frac{d x}{d t}=4 t-t^{2}=t(4-t) $

Thus, $v=0$ gives $t=0$ and/or $t=4$.

Now $v=0$ at $P$ as well as at $Q$ and at $P, t=0$. So, at $Q, t=4$. Thus, the car will reach the point $Q$ after 4 seconds. Also the distance travelled in 4 seconds is given by

$ x] _{t=4}=4^{2}(2-\frac{4}{3})=16(\frac{2}{3})=\frac{32}{3} m $

Example 31 A water tank has the shape of an inverted right circular cone with its axis vertical and vertex lowermost. Its semi-vertical angle is $\tan ^{-1}(0.5)$. Water is poured into it at a constant rate of 5 cubic metre per hour. Find the rate at which the level of the water is rising at the instant when the depth of water in the tank is $4 m$.

Solution Let $r, h$ and $\alpha$ be as in Fig 6.20. Then $\tan \alpha=\frac{r}{h}$.

So

$ \alpha=\tan ^{-1}(\frac{r}{h}) $

But

$ \alpha=\tan ^{-1}(0.5) $

(given)

or

$ \frac{r}{h}=0.5 $

or

$ r=\frac{h}{2} $

Let $V$ be the volume of the cone. Then

$ V=\frac{1}{3} \pi r^{2} h=\frac{1}{3} \pi(\frac{h}{2})^{2} h=\frac{\pi h^{3}}{12} $

Fig 6.20

Therefore

$ \begin{aligned} \frac{d V}{d t} & =\frac{d}{d h}(\frac{\pi h^{3}}{12}) \cdot \frac{d h}{d t} \\ & =\frac{\pi}{4} h^{2} \frac{d h}{d t} \end{aligned} $

Now rate of change of volume, i.e., $\frac{d V}{d t}=5 m^{3} / h$ and $h=4 m$.

Therefore

$ 5=\frac{\pi}{4}(4)^{2} \cdot \frac{d h}{d t} $

or

$ \frac{d h}{d t}=\frac{5}{4 \pi}=\frac{35}{88} m / h(\pi=\frac{22}{7}) $

Thus, the rate of change of water level is $\frac{35}{88} m / h$.

Example 32 A man of height 2 metres walks at a uniform speed of $5 km / h$ away from a lamp post which is 6 metres high. Find the rate at which the length of his shadow increases.

Solution In Fig 6.21, Let AB be the lamp-post, the lamp being at the position $B$ and let $MN$ be the man at a particular time $t$ and let $AM=l$ metres. Then, MS is the shadow of the man. Let MS $=s$ metres.

Note that

or

or

2 and $AB=6$ (given))

Thus

So

Therefore

$ \Delta MSN \sim \Delta ASB $

$ \frac{MS}{AS}=\frac{MN}{AB} $

$ AS=3 s(\text{ as } MN= $

Fig 6.21

Since $\frac{d l}{d t}=5 km / h$. Hence, the length of the shadow increases at the rate $\frac{5}{2} km / h$.

Example 33 Find intervals in which the function given by

$ f(x)=\frac{3}{10} x^{4}-\frac{4}{5} x^{3}-3 x^{2}+\frac{36}{5} x+11 $

is (a) increasing (b) decreasing.

Solution We have

$ f(x)=\frac{3}{10} x^{4}-\frac{4}{5} x^{3}-3 x^{2}+\frac{36}{5} x+11 $

Therefore

$ \begin{aligned} f^{\prime}(x) & =\frac{3}{10}(4 x^{3})-\frac{4}{5}(3 x^{2})-3(2 x)+\frac{36}{5} \\ & =\frac{6}{5}(x-1)(x+2)(x-3) \quad \text{ (on simplification) } \end{aligned} $

Now $f^{\prime}(x)=0$ gives $x=1, x=-2$, or $x=3$. The points $x=1,-2$, and 3 divide the real line into four disjoint intervals namely, $(-\infty,-2),(-2,1),(1,3)$ and $(3, \infty)$ (Fig 6.22).

Fig 6.22

Consider the interval $(-\infty,-2)$, i.e., when $-\infty<x<-2$.

In this case, we have $x-1<0, x+2<0$ and $x-3<0$.

(In particular, observe that for $x=-3, f^{\prime}(x)=(x-1)(x+2)(x-3)=(-4)(-1)$ $(-6)<0)$

Therefore, $\quad f^{\prime}(x)<0$ when $-\infty<x<-2$.

Thus, the function $f$ is decreasing in $(-\infty,-2)$.

Consider the interval $(-2,1)$, i.e., when $-2<x<1$.

In this case, we have $x-1<0, x+2>0$ and $x-3<0$

(In particular, observe that for $x=0, f^{\prime}(x)=(x-1)(x+2)(x-3)=(-1)(2)(-3)$ $=6>0)$

So

$ f^{\prime}(x)>0 \text{ when }-2<x<1 \text{. } $

Thus,

$ f \text{ is increasing in }(-2,1) \text{. } $

Now consider the interval $(1,3)$, i.e., when $1<x<3$. In this case, we have $x-1>0, x+2>0$ and $x-3<0$.

So,

$ f^{\prime}(x)<0 \text{ when } 1<x<3 \text{. } $

Thus, $f$ is decreasing in $(1,3)$.

Finally, consider the interval $(3, \infty)$, i.e., when $x>3$. In this case, we have $x-1>0$, $x+2>0$ and $x-3>0$. So $f^{\prime}(x)>0$ when $x>3$.

Thus, $f$ is increasing in the interval $(3, \infty)$.

Example 34 Show that the function $f$ given by

$ f(x)=\tan ^{-1}(\sin x+\cos x), x>0 $

is always an increasing function in $0, \frac{\pi}{4}$.

Solution We have

Therefore

$ f(x)=\tan ^{-1}(\sin x+\cos x), x>0 $

$ f^{\prime}(x)=\frac{1}{1+(\sin x+\cos x)^{2}}(\cos x-\sin x) $

$ =\frac{\cos x-\sin x}{2+\sin 2 x} $

Note that $2+\sin 2 x>0$ for all $x$ in $0, \frac{\pi}{4}$.

Therefore

$ f^{\prime}(x)>0 \text{ if } \cos x-\sin x>0 $

or

$ f^{\prime}(x)>0 \text{ if } \cos x>\sin x \text{ or } \cot x>1 $

Now

$ \cot x>1 \text{ if } \tan x<1 \text{, i.e., if } 0<x<\frac{\pi}{4} $

Thus

$ f^{\prime}(x)>0 \text{ in } 0, \frac{\pi}{4} $

Hence $f$ is increasing function in $(0, \frac{\pi}{4})$.

Example 35 A circular disc of radius $3 cm$ is being heated. Due to expansion, its radius increases at the rate of $0.05 cm / s$. Find the rate at which its area is increasing when radius is $3.2 cm$.

Solution Let $r$ be the radius of the given disc and $A$ be its area. Then

or

$ A=\pi r^{2} $

$ \frac{d A}{d t}=2 \pi r \frac{d r}{d t} $

Now approximate rate of increase of radius $=d r=\frac{d r}{d t} \Delta t=0.05 cm / s$.

Therefore, the approximate rate of increase in area is given by

$ \begin{aligned} d A & =\frac{d A}{d t}(\Delta t)=2 \pi r(\frac{d r}{d t} \Delta t) \\ & =2 \pi(3.2)(0.05)=0.320 \pi cm^{2} / s \quad(r=3.2 cm) \end{aligned} $

Example 36 An open topped box is to be constructed by removing equal squares from each corner of a 3 metre by 8 metre rectangular sheet of aluminium and folding up the sides. Find the volume of the largest such box.

Solution Let $x$ metre be the length of a side of the removed squares. Then, the height of the box is $x$, length is $8-2 x$ and breadth is $3-2 x$ (Fig 6.23). If $V(x)$ is the volume of the box, then

Fig 6.23

$ \begin{aligned} V(x) & =x(3-2 x)(8-2 x) \\ & =4 x^{3}-22 x^{2}+24 x \end{aligned} $

Therefore

$ \begin{cases} V^{\prime}(x)=12 x^{2}-44 x+24=4(x-3)(3 x-2) \\ V^{\prime \prime}(x)=24 x-44 \end{cases}. $

Now

$ V^{\prime}(x)=0 \text{ gives } x=3, \frac{2}{3} \text{. But } x \neq 3 \text{ (Why?) } $

Thus, we have $x=\frac{2}{3}$. Now $V^{\prime \prime}(\frac{2}{3})=24(\frac{2}{3})-44=-28<0$.

Therefore, $x=\frac{2}{3}$ is the point of maxima, i.e., if we remove a square of side $\frac{2}{3}$ metre from each corner of the sheet and make a box from the remaining sheet, then the volume of the box such obtained will be the largest and it is given by

$ \begin{aligned} V(\frac{2}{3}) & =4(\frac{2}{3})^{3}-22(\frac{2}{3})^{2}+24(\frac{2}{3}) \\ & =\frac{200}{27} m^{3} \end{aligned} $

Example 37 Manufacturer can sell $x$ items at a price of rupees $5-\frac{x}{100}$ each. The cost price of $x$ items is $Rs \frac{x}{5}+500$. Find the number of items he should sell to earn maximum profit.

Solution Let $S(x)$ be the selling price of $x$ items and let $C(x)$ be the cost price of $x$ items. Then, we have

$ S(x)=(5-\frac{x}{100}) x=5 x-\frac{x^{2}}{100} $

and

$ C(x)=\frac{x}{5}+500 $

Thus, the profit function $P(x)$ is given by

i.e.

$ \begin{aligned} & P(x)=S(x)-C(x)=5 x-\frac{x^{2}}{100}-\frac{x}{5}-500 \\ & P(x)=\frac{24}{5} x-\frac{x^{2}}{100}-500 \\ & P^{\prime}(x)=\frac{24}{5}-\frac{x}{50} \end{aligned} $

Now $P^{\prime}(x)=0$ gives $x=240$. Also $P^{\prime \prime}(x)=\frac{-1}{50}$. So $P^{\prime \prime}(240)=\frac{-1}{50}<0$

Thus, $x=240$ is a point of maxima. Hence, the manufacturer can earn maximum profit, if he sells 240 items.

Miscellaneous Exercise on Chapter 6

1. Show that the function given by $f(x)=\frac{\log x}{x}$ has maximum at $x=e$.

Solution

The given function is $f(x)=\frac{\log x}{x}$.

$ f^{\prime}(x)=\frac{x(\frac{1}{x})-\log x}{x^{2}}=\frac{1-\log x}{x^{2}} $

Now, $f^{\prime}(x)=0$

$\Rightarrow 1-\log x=0$ $\Rightarrow \log x=1$

$\Rightarrow \log x=\log e$

$\Rightarrow x=e$

Now, $f^{\prime \prime}(x)=\frac{x^{2}(-\frac{1}{x})-(1-\log x)(2 x)}{x^{4}}$

$ \begin{aligned} & =\frac{-x-2 x(1-\log x)}{x^{4}} \\ & =\frac{-3+2 \log x}{x^{3}} \end{aligned} $

Now, $f^{\prime \prime}(e)=\frac{-3+2 \log e}{e^{3}}=\frac{-3+2}{e^{3}}=\frac{-1}{e^{3}}<0$

Therefore, by second derivative test, $f$ is the maximum at $x=e$.

2. The two equal sides of an isosceles triangle with fixed base $b$ are decreasing at the rate of $3 cm$ per second. How fast is the area decreasing when the two equal sides are equal to the base?

Solution

Let $\triangle A B C$ be isosceles where $B C$ is the base of fixed length $b$.

Let the length of the two equal sides of $\triangle A B C$ be $a$.

Draw AD $\square BC$.

Now, in $\triangle A D C$, by applying the Pythagoras theorem, we have:

$AD=\sqrt{a^{2}-\frac{b^{2}}{4}}$

Area of triangle

$ (A)=\frac{1}{2} b \sqrt{a^{2}-\frac{b^{2}}{4}} $

The rate of change of the area with respect to time $(t)$ is given by,

$\frac{d A}{d t}=\frac{1}{2} b \cdot \frac{2 a}{2 \sqrt{a^{2}-\frac{b^{2}}{4}}} \frac{d a}{d t}=\frac{a b}{\sqrt{4 a^{2}-b^{2}}} \frac{d a}{d t}$

It is given that the two equal sides of the triangle are decreasing at the rate of $3 cm$ per second.

$ \begin{aligned} & \\ & \square \frac{d a}{d t}=-3 cm / s \\ & \therefore \frac{d A}{d t}=\frac{-3 a b}{\sqrt{4 a^{2}-b^{2}}} \end{aligned} $

Then, when $a=b$, we have:

$\frac{d A}{d t}=\frac{-3 b^{2}}{\sqrt{4 b^{2}-b^{2}}}=\frac{-3 b^{2}}{\sqrt{3 b^{2}}}=-\sqrt{3} b$

Hence, if the two equal sides are equal to the base, then the area of the triangle is decreasing at the rate of $\sqrt{3} bm cm^{2} / s$.

3. Find the intervals in which the function $f$ given by

$ f(x)=\frac{4 \sin x-2 x-x \cos x}{2+\cos x} $

is (i) increasing (ii) decreasing.

Solution

$f(x)=\frac{4 \sin x-2 x-x \cos x}{2+\cos x}$

$\therefore f^{\prime}(x)=\frac{(2+\cos x)(4 \cos x-2-\cos x+x \sin x)-(4 \sin x-2 x-x \cos x)(-\sin x)}{(2+\cos x)^{2}}$

$=\frac{(2+\cos x)(3 \cos x-2+x \sin x)+\sin x(4 \sin x-2 x-x \cos x)}{(2+\cos x)^{2}}$

$=\frac{6 \cos x-4+2 x \sin x+3 \cos ^{2} x-2 \cos x+x \sin x \cos x+4 \sin ^{2} x-2 x \sin x-x \sin x \cos x}{(2+\cos x)^{2}}$

$=\frac{4 \cos x-4+3 \cos ^{2} x+4 \sin ^{2} x}{(2+\cos x)^{2}}$

$=\frac{4 \cos x-4+3 \cos ^{2} x+4-4 \cos ^{2} x}{(2+\cos x)^{2}}$

$=\frac{4 \cos x-\cos ^{2} x}{(2+\cos x)^{2}}=\frac{\cos x(4-\cos x)}{(2+\cos x)^{2}}$

Now, $f^{\prime}(x)=0$

$\Rightarrow \cos x=0$ or $\cos x=4$

But, $\cos x \neq 4$

$\square \cos x=0$

$\Rightarrow x=\frac{\pi}{2}, \frac{3 \pi}{2}$

Now, $x=\frac{\pi}{2}$ and $x=\frac{3 \pi}{2}$ divides $(0,2 \pi)$ into three disjoint intervals i.e.,

$(0, \frac{\pi}{2}),(\frac{\pi}{2}, \frac{3 \pi}{2})$, and $(\frac{3 \pi}{2}, 2 \pi)$.

In intervals $(0, \frac{\pi}{2})$ and $(\frac{3 \pi}{2}, 2 \pi), f^{\prime}(x)>0$.

Thus, $f(x)$ is increasing for $0<x<\frac{x}{2}$ and $\frac{3 \pi}{2}<x<2 \pi$.

In the interval $(\frac{\pi}{2}, \frac{3 \pi}{2}), f^{\prime}(x)<0$.

Thus, $f(x)$ is decreasing for $\frac{\pi}{2}<x<\frac{3 \pi}{2}$.

4. Find the intervals in which the function $f$ given by $f(x)=x^{3}+\frac{1}{x^{3}}, x \neq 0$ is (i) increasing (ii) decreasing.

Solution

$f(x)=x^{3}+\frac{1}{x^{3}}$

$\therefore f^{\prime}(x)=3 x^{2}-\frac{3}{x^{4}}=\frac{3 x^{6}-3}{x^{4}}$

Then, $f^{\prime}(x)=0 \Rightarrow 3 x^{6}-3=0 \Rightarrow x^{6}=1 \Rightarrow x= \pm 1$

Now, the points $x=1$ and $x=-1$ divide the real line into three disjoint intervals

i.e., $(-\infty,-1),(-1,1)$, and $(1, \infty)$.

In intervals $(-\infty,-1)$ and $(1, \infty)$ i.e., when $x<-1$ and $x>1, f^{\prime}(x)>0$.

Thus, when $x<-1$ and $x>1, f$ is increasing.

In interval $(-1,1)$ i.e., when $-1<x<1, f^{\prime}(x)<0$.

Thus, when $-1<x<1, f$ is decreasing.

5. Find the maximum area of an isosceles triangle inscribed in the ellipse $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ with its vertex at one end of the major axis.

Solution

The given ellipse is $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$.

Let the major axis be along the $x$-axis.

Let $A B C$ be the triangle inscribed in the ellipse where vertex $C$ is at $(a, 0)$.

Since the ellipse is symmetrical with respect to the $x$-axis and $y$-axis, we can assume the coordinates of $A$ to be $(-x_1, y_1)$ and the coordinates of $B$ to be $(-x_1,-y_1)$.

Now, we have $y_1= \pm \frac{b}{a} \sqrt{a^{2}-x_1^{2}}$.

$\square$ Coordinates of $A$ are $(-x_1, \frac{b}{a} \sqrt{a^{2}-x_1^{2}})$ and the coordinates of $B$ are $(x_1,-\frac{b}{a} \sqrt{a^{2}-x_1^{2}})$.

As the point $(x_1, y_1)$ lies on the ellipse, the area of triangle $ABC(A)$ is given by,

$ \begin{aligned} & A=\frac{1}{2}|a(\frac{2 b}{a} \sqrt{a^{2}-x_1^{2}})+(-x_1)(-\frac{b}{a} \sqrt{a^{2}-x_1^{2}})+(-x_1)(-\frac{b}{a} \sqrt{a^{2}-x_1^{2}})| \\ & \Rightarrow A=b \sqrt{a^{2}-x_1^{2}}+x_1 \frac{b}{a} \sqrt{a^{2}-x_1^{2}} \\ & \therefore \frac{d A}{d x_1}=\frac{-2 x_1 b}{2 \sqrt{a^{2}-x_1^{2}}}+\frac{b}{a} \sqrt{a^{2}-x_1^{2}}-\frac{2 b x_1^{2}}{a 2 \sqrt{a^{2}-x_1^{2}}} \\ & =\frac{b}{a \sqrt{a^{2}-x_1^{2}}}[-x_1 a+(a^{2}-x_1^{2})-x_1^{2}] \\ & =\frac{b(-2 x_1^{2}-x_1 a+a^{2})}{a \sqrt{a^{2}-x_1^{2}}} \end{aligned} $

Now, $\frac{d A}{d x_1}=0$

$\Rightarrow-2 x_1^{2}-x_1 a+a^{2}=0$

$\Rightarrow x_1=\frac{a \pm \sqrt{a^{2}-4(-2)(a^{2})}}{2(-2)}$

$=\frac{a \pm \sqrt{9 a^{2}}}{-4}$

$=\frac{a \pm 3 a}{-4}$

$\Rightarrow x_1=-a, \frac{a}{2}$

But, $x_1$ cannot be equal to $a$. $\therefore x_1=\frac{a}{2} \Rightarrow y_1=\frac{b}{a} \sqrt{a^{2}-\frac{a^{2}}{4}}=\frac{b a}{2 a} \sqrt{3}=\frac{\sqrt{3} b}{2}$

Now, $\frac{d^{2} A}{d x_1^{2}}=\frac{b}{a}{\frac{\sqrt{a^{2}-x_1^{2}}(-4 x_1-a)-(-2 x_1^{2}-x_1 a+a^{2}) \frac{(-2 x_1)}{2 \sqrt{a^{2}-x_1^{2}}}}{a^{2}-x_1^{2}}}$

$ =\frac{b}{a}{\frac{(a^{2}-x_1^{2})(-4 x_1-a)+x_1(-2 x_1^{2}-x_1 a+a^{2})}{(a^{2}-x_1^{2})^{\frac{3}{2}}}} $

$ =\frac{b}{a}{\frac{2 x^{3}-3 a^{2} x-a^{3}}{(a^{2}-x_1^{2})^{\frac{3}{2}}}} $

Also, when $x_1=\frac{a}{2}$, then

$ \begin{aligned} \frac{d^{2} A}{d x_1^{2}} & =\frac{b}{a}{\frac{2 \frac{a^{3}}{8}-3 \frac{a^{3}}{2}-a^{3}}{(\frac{3 a^{2}}{4})^{\frac{3}{2}}}}=\frac{b}{a}{\frac{\frac{a^{3}}{4}-\frac{3}{2} a^{3}-a^{3}}{(\frac{3 a^{2}}{4})^{\frac{3}{2}}}} \\ & =-\frac{b}{a}{\frac{\frac{9}{4} a^{3}}{(\frac{3 a^{2}}{4})^{\frac{3}{2}}}}<0 \end{aligned} $

Thus, the area is the maximum when $x_1=\frac{a}{2}$.

$\square$ Maximum area of the triangle is given by,

$ \begin{aligned} A & =b \sqrt{a^{2}-\frac{a^{2}}{4}}+(\frac{a}{2}) \frac{b}{a} \sqrt{a^{2}-\frac{a^{2}}{4}} \\ & =a b \frac{\sqrt{3}}{2}+(\frac{a}{2}) \frac{b}{a} \times \frac{a \sqrt{3}}{2} \\ & =\frac{a b \sqrt{3}}{2}+\frac{a b \sqrt{3}}{4}=\frac{3 \sqrt{3}}{4} a b \end{aligned} $

6. A tank with rectangular base and rectangular sides, open at the top is to be constructed so that its depth is $2 m$ and volume is $8 m^{3}$. If building of tank costs Rs 70 per sq metres for the base and Rs 45 per square metre for sides. What is the cost of least expensive tank?

Solution

Let $l, b$, and $h$ represent the length, breadth, and height of the tank respectively.

Then, we have height $(h)=2 m$

Volume of the tank $=8 m^{3}$

Volume of the tank $=l \times b \times h$

$\square 8=l \times b \times 2$

$\Rightarrow l b=4 \Rightarrow b=\frac{4}{l}$

Now, area of the base $=I b=4$

Area of the 4 walls $(A)=2 h(I+b)$

$\therefore A=4(l+\frac{4}{l})$

$\Rightarrow \frac{d A}{d l}=4(1-\frac{4}{l^{2}})$

Now, $\frac{d A}{d l}=0$

$\Rightarrow 1-\frac{4}{l^{2}}=0$

$\Rightarrow l^{2}=4$

$\Rightarrow l= \pm 2$

However, the length cannot be negative.

Therefore, we have $I=4$.

$\therefore b=\frac{4}{l}=\frac{4}{2}=2$

Now, $\frac{d^{2} A}{d l^{2}}=\frac{32}{l^{3}}$

When $l=2, \frac{d^{2} A}{d l^{2}}=\frac{32}{8}=4>0$.

Thus, by second derivative test, the area is the minimum when $I=2$.

We have $I=b=h=2$.

$\square$ Cost of building the base $=Rs 70 \times(I b)=Rs 70(4)=Rs 280$

Cost of building the walls $=Rs 2 h(I+b) \times 45=Rs 90(2)(2+2)$

$=Rs 8(90)=Rs 720$

Required total cost $=Rs(280+720)=Rs 1000$

Hence, the total cost of the tank will be Rs 1000.

7. The sum of the perimeter of a circle and square is $k$, where $k$ is some constant. Prove that the sum of their areas is least when the side of square is double the radius of the circle.

Solution

Let $r$ be the radius of the circle and $a$ be the side of the square.

Then, we have:

$2 \pi r+4 a=k$ (where $k$ is constant)

$\Rightarrow a=\frac{k-2 \pi r}{4}$

The sum of the areas of the circle and the square $(A)$ is given by,

$A=\pi r^{2}+a^{2}=\pi r^{2}+\frac{(k-2 \pi r)^{2}}{16}$

$\therefore \frac{d A}{d r}=2 \pi r+\frac{2(k-2 \pi r)(-2 \pi)}{16}=2 \pi r-\frac{\pi(k-2 \pi r)}{4}$

Now, $\frac{d A}{d r}=0$

$\Rightarrow 2 \pi r=\frac{\pi(k-2 \pi r)}{4}$

$8 r=k-2 \pi r$

$\Rightarrow(8+2 \pi) r=k$

$\Rightarrow r=\frac{k}{8+2 \pi}=\frac{k}{2(4+\pi)}$

Now, $\frac{d^{2} A}{d r^{2}}=2 \pi+\frac{\pi^{2}}{2}>0$

$\therefore$ When $r=\frac{k}{2(4 \pi)}, \frac{d^{2} A}{d r^{2}}>0$.

When $r=\frac{k}{2(4 \pi)}, a=\frac{k-2 \pi[\frac{k}{2(4 \pi)}]}{4}=\frac{k(4 \pi) \pi k}{4(\pi)}=\frac{4 k}{4(\pi)}=\frac{k}{\pi}=2 r$.

Hence, it has been proved that the sum of their areas is least when the side of the square is double the radius of the circle.

8. A window is in the form of a rectangle surmounted by a semicircular opening. The total perimeter of the window is $10 m$. Find the dimensions of the window to admit maximum light through the whole opening.

Solution

Let $x$ and $y$ be the length and breadth of the rectangular window.

Radius of the semicircular opening $=\frac{x}{2}$

It is given that the perimeter of the window is $10 m$.

$\therefore x+2 y+\frac{\pi x}{2}=10$

$\Rightarrow x(1+\frac{\pi}{2})+2 y=10$

$\Rightarrow 2 y=10-x(1+\frac{\pi}{2})$

$\Rightarrow y=5-x(\frac{1 \pi}{2}+\frac{-}{4})$

$\square$ Area of the window $(A)$ is given by,

$ \begin{aligned} A & =x y+\frac{\pi}{2}(\frac{x}{2})^{2} \\ & =x[5-x(\frac{1 \pi}{2}+\frac{\pi}{4})]+\frac{x^{2}}{8} \\ & =5 x-x^{2}(\frac{1 \pi}{2}+\frac{\pi}{4})+\frac{\pi}{8} x^{2} \\ \therefore & \frac{d A}{d x}=5-2 x(\frac{1 \pi}{2}+\frac{\pi}{4})+\frac{\pi}{4} x \\ & =5-x(1+\frac{\pi}{2})+\frac{\pi}{4} x \\ \therefore & \frac{d^{2} A}{d x^{2}}=-(1+\frac{\pi}{2})+\frac{\pi}{4}=-1-\frac{\pi}{4} \end{aligned} $

Now, $\frac{d A}{d x}=0$

$\Rightarrow 5-x(1+\frac{\pi}{2})+\frac{\pi}{4} x=0$

$\Rightarrow 5-x-\frac{\pi}{4} x=0$

$\Rightarrow x(1+\frac{\pi}{4})=5$

$\Rightarrow x=\frac{5}{(1+\frac{\pi}{4})}=\frac{20}{\pi+4}$

Thus, when $x=\frac{20}{\pi+4}$ then $\frac{d^{2} A}{d x^{2}}<0$.

Therefore, by second derivative test, the area is the maximum when length $x=\frac{20}{\pi+4} m$. Now,

$y=5-\frac{20}{\pi+4}(\frac{2+\pi}{4})=5-\frac{5(2+\pi)}{\pi+4}=\frac{10}{\pi+4} m$

Hence, the required dimensions of the window to admit maximum light is given

by length $=\frac{20}{\pi+4} m$ and breadth $=\frac{10}{\pi+4} m$.

9. A point on the hypotenuse of a triangle is at distance $a$ and $b$ from the sides of the triangle.

Show that the minimum length of the hypotenuse is $(a^{\frac{2}{3}}+b^{\frac{2}{3}})^{\frac{3}{2}}$.

Solution

Let $\triangle A B C$ be right-angled at $B$. Let $A B=x$ and $B C=y$.

Let $P$ be a point on the hypotenuse of the triangle such that $P$ is at a distance of $a$ and $b$ from the sides $A B$ and $B C$ respectively.

Let $\square C=\theta$.

We have,

$AC=\sqrt{x^{2}+y^{2}}$

Now,

$PC=b cosec \theta$

And, $AP=a \sec \theta$

$\square AC=AP+PC$

$\square AC=b cosec \theta+a \sec \theta \ldots$ (1)

$\therefore \frac{d(AC)}{d \theta}=-b cosec \theta \cot \theta+a \sec \theta \tan \theta$

$\therefore \frac{d(AC)}{d \theta}=0$

$\Rightarrow a \sec \theta \tan \theta=b cosec \theta \cot \theta$

$\Rightarrow \frac{a}{\cos \theta} \cdot \frac{\sin \theta}{\cos \theta}=\frac{b}{\sin \theta} \frac{\cos \theta}{\sin \theta}$

$\Rightarrow a \sin ^{3} \theta=b \cos ^{3} \theta$

$\Rightarrow(a)^{\frac{1}{3}} \sin \theta=(b)^{\frac{1}{3}} \cos \theta$

$\Rightarrow \tan \theta=(\frac{b}{a})^{\frac{1}{3}}$

$\therefore \sin \theta=\frac{(b)^{\frac{1}{3}}}{\sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}}$ and $\cos \theta=\frac{(a)^{\frac{1}{3}}}{\sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}}$

It can be clearly shown that $\frac{d^{2}(AC)}{d \theta^{2}}<0$ when $\tan \theta=(\frac{b}{a})^{\frac{1}{3}}$.

Therefore, by second derivative test, the length of the hypotenuse is the maximum when

$\tan \theta=(\frac{b}{a})^{\frac{1}{3}}$.

Now, when $\tan \theta=(\frac{b}{a})^{\frac{1}{3}}$, we have:

$ \begin{aligned} AC & =\frac{b \sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}}{b^{\frac{1}{3}}}+\frac{a \sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}}{a^{\frac{1}{3}}} \\ & =\sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}(b^{\frac{2}{3}}+a^{\frac{2}{3}}) \\ & =(a^{\frac{2}{3}}+b^{\frac{2}{3}})^{\frac{3}{2}} \end{aligned} $

Hence, the maximum length of the hypotenuses is $(a^{\frac{2}{3}}+b^{\frac{2}{3}})^{\frac{3}{2}}$.

10. Find the points at which the function $f$ given by $f(x)=(x-2)^{4}(x+1)^{3}$ has

$\begin{matrix} \text{ (i) local maxima } & \text{ (ii) local minima }\end{matrix} $

(iii) point of inflexion

Solution

The given function is $f(x)=(x-2)^{4}(x+1)^{3}$.

$ \begin{aligned} \therefore f^{\prime}(x) & =4(x-2)^{3}(x+1)^{3}+3(x+1)^{2}(x-2)^{4} \\ & =(x-2)^{3}(x+1)^{2}[4(x+1)+3(x-2)] \\ & =(x-2)^{3}(x+1)^{2}(7 x-2) \end{aligned} $

Now, $f^{\prime}(x)=0 \Rightarrow x=-1$ and $x=\frac{2}{7}$ or $x=2$

Now, for values of $x$ close to $\frac{2}{7}$ and to the left of $\frac{2}{7}, f^{\prime}(x)>0$. Also, for values of $x$ close to $\frac{2}{7}$ and to the right of $\frac{2}{7}, f^{\prime}(x)<0$.

Thus, $x=\frac{2}{7}$ is the point of local maxima.

Now, for values of $x$ close to 2 and to the left of $2, f^{\prime}(x)<0$. Also, for values of $x$ close to 2 and to the right of $2, f^{\prime}(x)>0$.

Thus, $x=2$ is the point of local minima.

Now, as the value of $x$ varies through $-1, f^{\prime}(x)$ does not changes its sign.

Thus, $x=-1$ is the point of inflexion.

11. Find the absolute maximum and minimum values of the function $f$ given by

$ f(x)=\cos ^{2} x+\sin x, x \in[0, \pi] $

Solution

$ \begin{aligned} f(x) & =\cos ^{2} x+\sin x \\ f^{\prime}(x) & =2 \cos x(-\sin x)+\cos x \\ & =-2 \sin x \cos x+\cos x \end{aligned} $

Now, $f^{\prime}(x)=0$

$\Rightarrow 2 \sin x \cos x=\cos x \Rightarrow \cos x(2 \sin x-1)=0$

$\Rightarrow \sin x=\frac{1}{2}$ or $\cos x=0$

$\Rightarrow x=\frac{\pi}{6}$, or $\frac{\pi}{2}$ as $x \in[0, \pi]$

Now, evaluating the value of $f$ at critical points $x=\frac{\pi}{2}$ and $x=\frac{\pi}{6}$ and at the end points of

the interval $[0, \pi]$ (i.e., at $x=0$ and $x=\pi$ ), we have: $f(\frac{\pi}{6})=\cos ^{2} \frac{\pi}{6}+\sin \frac{\pi}{6}=(\frac{\sqrt{3}}{2})^{2}+\frac{1}{2}=\frac{5}{4}$

$f(0)=\cos ^{2} 0+\sin 0=1+0=1$

$f(\pi)=\cos ^{2} \pi+\sin \pi=(-1)^{2}+0=1$

$f(\frac{\pi}{2})=\cos ^{2} \frac{\pi}{2}+\sin \frac{\pi}{2}=0+1=1$

Hence, the absolute maximum value of $f$ is $\frac{5}{4}$ occurring at $x=\frac{\pi}{6}$ and the absolute minimum value of $f$ is 1 occurring at $x=0, \frac{\pi}{2}$, and $\pi$.

12. Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius $r$ is $\frac{4 r}{3}$.

Solution

A sphere of fixed radius $(r)$ is given.

Let $R$ and $h$ be the radius and the height of the cone respectively.

The volume $(V)$ of the cone is given by,

$V=\frac{1}{3} \pi R^{2} h$

Now, from the right triangle $B C D$, we have:

$BC=\sqrt{r^{2}-R^{2}}$

$\square h=r+\sqrt{r^{2}-R^{2}}$

$ \begin{aligned} & \therefore V=\frac{1}{3} \pi R^{2}(r+\sqrt{r^{2}-R^{2}})=\frac{1}{3} \pi R^{2} r+\frac{1}{3} \pi R^{2} \sqrt{r^{2}-R^{2}} \\ & \begin{aligned} \therefore \frac{d V}{d R} & =\frac{2}{3} \pi R r+\frac{2 \pi}{3} \pi R \sqrt{r^{2}-R^{2}}+\frac{R^{2}}{3} \cdot \frac{(-2 R)}{2 \sqrt{r^{2}-R^{2}}} \\ & =\frac{2}{3} \pi R r+\frac{2 \pi}{3} \pi R \sqrt{r^{2}-R^{2}}-\frac{R^{3}}{3 \sqrt{r^{2}-R^{2}}} \\ & =\frac{2}{3} \pi R r+\frac{2 \pi R(r^{2}-R^{2})-\pi R^{3}}{3 \sqrt{r^{2}-R^{2}}} \\ & =\frac{2}{3} \pi R r+\frac{2 \pi R r^{2}-3 \pi R^{3}}{3 \sqrt{r^{2}-R^{2}}} \end{aligned} \end{aligned} $

Now, $\frac{d V}{d R^{2}}=0$

$\Rightarrow \frac{2 \pi r R}{3}=\frac{3 \pi R^{3}-2 \pi R r^{2}}{3 \sqrt{r^{2}-R^{2}}}$

$\Rightarrow 2 r \sqrt{r^{2}-R^{2}}=3 R^{2}-2 r^{2}$

$\Rightarrow 4 r^{2}(r^{2}-R^{2})=(3 R^{2}-2 r^{2})^{2}$

$\Rightarrow 4 r^{4}-4 r^{2} R^{2}=9 R^{4}+4 r^{4}-12 R^{2} r^{2}$

$\Rightarrow 9 R^{4}-8 r^{2} R^{2}=0$

$\Rightarrow 9 R^{2}=8 r^{2}$

$\Rightarrow R^{2}=\frac{8 r^{2}}{9}$

Now, $\frac{d^{2} V}{d R^{2}}=\frac{2 \pi r}{3}+\frac{3 \sqrt{r^{2}-R^{2}}(2 \pi r^{2}-9 \pi R^{2})-(2 \pi R r^{2}-3 \pi R^{3})(-6 R) \frac{1}{2 \sqrt{r^{2}-R^{2}}}}{9(r^{2}-R^{2})}$

$ =\frac{2 \pi r}{3}+\frac{3 \sqrt{r^{2}-R^{2}}(2 \pi r^{2}-9 \pi R^{2})+(2 \pi R r^{2}-3 \pi R^{3})(3 R) \frac{1}{2 \sqrt{r^{2}-R^{2}}}}{9(r^{2}-R^{2})} $

Now, when $R^{2}=\frac{8 r^{2}}{9}$, it can be shown that $\frac{d^{2} V}{d R^{2}}<0$.

$\square$ The volume is the maximum when

$ R^{2}=\frac{8 r^{2}}{9} $

When $R^{2}=\frac{8 r^{2}}{9}$, height of the cone $=r+\sqrt{r^{2}-\frac{8 r^{2}}{9}}=r+\sqrt{\frac{r^{2}}{9}}=r+\frac{r}{3}=\frac{4 r}{3}$.

Hence, it can be seen that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius $r$ is $\frac{4 r}{3}$.

13. Let $f$ be a function defined on $[a, b]$ such that $f^{\prime}(x)>0$, for all $x \in(a, b)$. Then prove that $f$ is an increasing function on $(a, b)$.

Solution

Let us take any 2 points $\mathrm{c}_1$ and $\mathrm{c}_2$ such that

${\mathrm{c} _1, \mathrm{c} _2} \in(\mathrm{a}, \mathrm{b})$ and

$\mathrm{c} _2=\mathrm{c} _1+\mathrm{h}$,

where $\mathrm{h} \rightarrow \mathrm{O}$

Now, $f^{\prime}\left(c _1\right)=\lim _{h \rightarrow 0} \frac{f\left(c _1+h\right)-f\left(c _1\right)}{h}=\frac{f\left(c _2\right)-f\left(c _1\right)}{c _2-c _1}$

Now, it is given that $\mathrm{f}^{\prime}(\mathrm{x})>0 \quad \forall \mathrm{x} \in(\mathrm{a}, \mathrm{b})$. Therefore, $\mathrm{f}^{\prime}\left(\mathrm{c}_1\right)>0$

$\Rightarrow \frac{\mathrm{f}\left(\mathrm{c}_2\right)-\mathrm{f}\left(\mathrm{c}_1\right)}{\mathrm{c}_2-\mathrm{c}_1}>\mathrm{O}$

From the above fraction, we can conclude that:

1. For $\mathrm{c}_2>\mathrm{c}_1, \mathrm{f}\left(\mathrm{c}_2\right)>\mathrm{f}\left(\mathrm{c}_1\right)$
2. For $c_1>c_2, f\left(c_1\right)>f\left(c_2\right)$

Hence, $\mathrm{f}(\mathrm{x})$ is an increasing function in $(\mathrm{a}, \mathrm{b})$.

14. Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius $R$ is $\frac{2 R}{\sqrt{3}}$. Also find the maximum volume.

Solution

A sphere of fixed radius $(R)$ is given.

Let $r$ and $h$ be the radius and the height of the cylinder respectively.

From the given figure, we have $h=2 \sqrt{R^{2}-r^{2}}$.

The volume $(V)$ of the cylinder is given by,

$ \begin{aligned} & V=\pi r^{2} h=2 \pi r^{2} \sqrt{R^{2}-r^{2}} \\ & \begin{aligned} \therefore \frac{d V}{d r} & =4 \pi r \sqrt{R^{2}-r^{2}}+\frac{2 \pi r^{2}(-2 r)}{2 \sqrt{R^{2}-r^{2}}} \\ & =4 \pi r \sqrt{R^{2}-r^{2}}-\frac{2 \pi r^{3}}{\sqrt{R^{2}-r^{2}}} \\ & =\frac{4 \pi r(R^{2}-r^{2})-2 \pi r^{3}}{\sqrt{R^{2}-r^{2}}} \\ & =\frac{4 \pi r R^{2}-6 \pi r^{3}}{\sqrt{R^{2}-r^{2}}} \end{aligned} \end{aligned} $

Now, $\frac{d V}{d r}=0 \Rightarrow 4 \pi r R^{2}-6 \pi r^{3}=0$

$\Rightarrow r^{2}=\frac{2 R^{2}}{3}$

Now, $\frac{d^{2} V}{d r^{2}}=\frac{\sqrt{R^{2}-r^{2}}(4 \pi R^{2}-18 \pi r^{2})-(4 \pi r R^{2}-6 \pi r^{3}) \frac{(-2 r)}{2 \sqrt{R^{2}-r^{2}}}}{(R^{2}-r^{2})}$

$ \begin{aligned} & =\frac{(R^{2}-r^{2})(4 \pi R^{2}-18 \pi r^{2})+r(4 \pi r R^{2}-6 \pi r^{3})}{(R^{2}-r^{2})^{\frac{3}{2}}} \\ & =\frac{4 \pi R^{4}-22 \pi r^{2} R^{2}+12 \pi r^{4}+4 \pi r^{2} R^{2}}{(R^{2}-r^{2})^{\frac{3}{2}}} \end{aligned} $

Now, it can be observed that at $r^{2}=\frac{2 R^{2}}{3}, \frac{d^{2} V}{d r^{2}}<0$.

$\square$ The volume is the maximum when $r^{2}=\frac{2 R^{2}}{3}$.

When $r^{2}=\frac{2 R^{2}}{3}$, the height of the cylinder is $2 \sqrt{R^{2}-\frac{2 R^{2}}{3}}=2 \sqrt{\frac{R^{2}}{3}}=\frac{2 R}{\sqrt{3}}$.

Hence, the volume of the cylinder is the maximum when the height of the cylinder is $\frac{2 R}{\sqrt{3}}$.

15. Show that height of the cylinder of greatest volume which can be inscribed in a right circular cone of height $h$ and semi vertical angle $\alpha$ is one-third that of the cone and the greatest volume of cylinder is $\frac{4}{27} \pi h^{3} \tan ^{2} \alpha$.

Solution

The given right circular cone of fixed height $(h)$ and semi-vertical angle ( $a$ ) can be drawn as:

Here, a cylinder of radius $R$ and height $H$ is inscribed in the cone.

Then, $\square GAO=a, OG=r, OA=h, OE=R$, and $CE=H$.

We have,

$r=h \tan a$

Now, since $\triangle AOG$ is similar to $\triangle CEG$, we have:

$\frac{AO}{OG}=\frac{CE}{EG}$

$\Rightarrow \frac{h}{r}=\frac{H}{r-R} \quad[EG=OG-OE]$

$\Rightarrow H=\frac{h}{r}(r-R)=\frac{h}{h \tan \alpha}(h \tan \alpha-R)=\frac{1}{\tan \alpha}(h \tan \alpha-R)$

Now, the volume $(V)$ of the cylinder is given by,

$V=\pi R^{2} H=\frac{\pi R^{2}}{\tan \alpha}(h \tan \alpha-R)=\pi R^{2} h-\frac{\pi R^{3}}{\tan \alpha}$

$\therefore \frac{d V}{d R}=2 \pi R h-\frac{3 \pi R^{2}}{\tan \alpha}$

Now, $\frac{d V}{d R}=0$

$\Rightarrow 2 \pi R h=\frac{3 \pi R^{2}}{\tan \alpha}$

$\Rightarrow 2 h \tan \alpha=3 R$

$\Rightarrow R=\frac{2 h}{3} \tan \alpha$

Now, $\frac{d^{2} V}{d R^{2}}=2 \pi h-\frac{6 \pi R}{\tan \alpha}$

And, for $R=\frac{2 h}{3} \tan \alpha$, we have:

$\frac{d^{2} V}{d R^{2}}=2 \pi h-\frac{6 \pi}{\tan \alpha}(\frac{2 h}{3} \tan \alpha)=2 \pi h-4 \pi h=-2 \pi h<0$

$\square$ By second derivative test, the volume of the cylinder is the greatest when

$R=\frac{2 h}{3} \tan \alpha$.

When $R=\frac{2 h}{3} \tan \alpha, H=\frac{1}{\tan \alpha}(h \tan \alpha-\frac{2 h}{3} \tan \alpha)=\frac{1}{\tan \alpha}(\frac{h \tan \alpha}{3})=\frac{h}{3}$.

Thus, the height of the cylinder is one-third the height of the cone when the volume of the cylinder is the greatest.

Now, the maximum volume of the cylinder can be obtained as:

$\pi(\frac{2 h}{3} \tan \alpha)^{2}(\frac{h}{3})=\pi(\frac{4 h^{2}}{9} \tan ^{2} \alpha)(\frac{h}{3})=\frac{4}{27} \pi h^{3} \tan ^{2} \alpha$

Hence, the given result is proved.

16. A cylindrical tank of radius $10 m$ is being filled with wheat at the rate of 314 cubic metre per hour. Then the depth of the wheat is increasing at the rate of

(A) $1 m / h$

(B) $0.1 m / h$

(C) $1.1 m / h$

(D) $0.5 m / h$

Solution

Let $r$ be the radius of the cylinder.

Then, volume $(V)$ of the cylinder is given by,

$V=\pi(\text{ radius })^{2} \times$ height

$ \begin{matrix} =\pi(10)^{2} h & (\text{ radius }=10 m) \\ =100 \pi h \end{matrix} $

Differentiating with respect to time $t$, we have:

$\frac{d V}{d t}=100 \pi \frac{d h}{d t}$

The tank is being filled with wheat at the rate of 314 cubic metres per hour.

$ \square \frac{d V}{d t}=314 m^{3} / h $

Thus, we have:

$ \begin{aligned} & 314=100 \pi \frac{d h}{d t} \\ & \Rightarrow \frac{d h}{d t}=\frac{314}{100(3.14)}=\frac{314}{314}=1 \end{aligned} $

Hence, the depth of wheat is increasing at the rate of $1 m / h$.

The correct answer is $A$.

Summary

If a quantity y varies with another quantity x, satisfying some rule y= f(x),then $ \frac{dy}{dx}or (f’(x)) $ represents the rate of change of y with tespect to x and $ \frac{dy}dx _{x=x0} or(f’(x_0))$\ text{represents the rate of change of y with respect to x at}$ $ x=x+0 $ $

If two variables $x$ and $y$ are varying with respect to another variable $t$, i.e., if $x=f(t)$ and $y=g(t)$, then by Chain Rule

$ \frac{d y}{d x}=\frac{d y}{d t} / \frac{d x}{d t}, \text{ if } \frac{d x}{d t} \neq 0 . $

A function $f$ is said to be

(a) increasing on an interval $(a, b)$ if $x_1<x_2$ in $(a, b) \Rightarrow f(x_1)<f(x_2)$ for all $x_1, x_2 \in(a, b)$.

Alternatively, if $f^{\prime}(x) \geq 0$ for each $x$ in $(a, b)$

(b) decreasing on $(a, b)$ if

$ x_1<x_2 \text{ in }(a, b) \Rightarrow f(x_1)>f(x_2) \text{ for all } x_1, x_2 \in(a, b) \text{. } $

(c) constant in $(a, b)$, if $f(x)=c$ for all $x \in(a, b)$, where $c$ is a constant.

• A point $c$ in the domain of a function $f$ at which either $f^{\prime}(c)=0$ or $f$ is not differentiable is called a critical point of $f$.
• First Derivative Test Let $f$ be a function defined on an open interval I. Let $f$ be continuous at a critical point $c$ in $I$. Then

(i) If $f^{\prime}(x)$ changes sign from positive to negative as $x$ increases through $c$, i.e., if $f^{\prime}(x)>0$ at every point sufficiently close to and to the left of $c$, and $f^{\prime}(x)<0$ at every point sufficiently close to and to the right of $c$, then $c$ is a point of local maxima. (ii) If $f^{\prime}(x)$ changes sign from negative to positive as $x$ increases through $c$, i.e., if $f^{\prime}(x)<0$ at every point sufficiently close to and to the left of $c$, and $f^{\prime}(x)>0$ at every point sufficiently close to and to the right of $c$, then $c$ is a point of local minima.

(iii) If $f^{\prime}(x)$ does not change sign as $x$ increases through $c$, then $c$ is neither a point of local maxima nor a point of local minima. Infact, such a point is called point of inflexion.

Second Derivative Test Let $f$ be a function defined on an interval I and $c \in I$. Let $f$ be twice differentiable at $c$. Then

(i) $x=c$ is a point of local maxima if $f^{\prime}(c)=0$ and $f^{\prime \prime}(c)<0$

The values $f(c)$ is local maximum value of $f$.

(ii) $x=c$ is a point of local minima if $f^{\prime}(c)=0$ and $f^{\prime \prime}(c)>0$

In this case, $f(c)$ is local minimum value of $f$.

(iii) The test fails if $f^{\prime}(c)=0$ and $f^{\prime \prime}(c)=0$.

In this case, we go back to the first derivative test and find whether $c$ is a point of maxima, minima or a point of inflexion.

Working rule for finding absolute maxima and/or absolute minima

Step 1: Find all critical points of $f$ in the interval, i.e., find points $x$ where either $f^{\prime}(x)=0$ or $f$ is not differentiable.

Step 2:Take the end points of the interval.

Step 3: At all these points (listed in Step 1 and 2), calculate the values of $f$.

Step 4: Identify the maximum and minimum values of $f$ out of the values calculated in Step 3. This maximum value will be the absolute maximum value of $f$ and the minimum value will be the absolute minimum value of $f$.