DETERMINANTS

Introduction

In the previous chapter, we have studied about matrices and algebra of matrices. We have also learnt that a system of algebraic equations can be expressed in the form of matrices. This means, a system of linear equations like

$ \begin{aligned} & a_1 x+b_1 y=c_1 \\ & a_2 x+b_2 y=c_2 \end{aligned} $

can be represented as $\begin{vmatrix}a_1 & b_1 \\ a_2 & b_2\end{vmatrix}\begin{vmatrix}x \\ y\end{vmatrix}=\begin{vmatrix}c_1 \\ c_2\end{vmatrix}$. Now, this system of equations has a unique solution or not, is determined by the number $a_1 b_2-a_2 b_1$. (Recall that if $\frac{a_1}{a_2} \neq \frac{b_1}{b_2}$ or, $a_1 b_2-a_2 b_1 \neq 0$, then the system of linear

P.S. Laplace

$(1749-1827)$ equations has a unique solution). The number $a_1 b_2-a_2 b_1$ which determines uniqueness of solution is associated with the matrix $A=\begin{vmatrix}a_1 & b_1 \\ a_2 & b_2\end{vmatrix}$ and is called the determinant of A or det A. Determinants have wide applications in Engineering, Science, Economics, Social Science, etc.

In this chapter, we shall study determinants up to order three only with real entries. Also, we will study various properties of determinants, minors, cofactors and applications of determinants in finding the area of a triangle, adjoint and inverse of a square matrix, consistency and inconsistency of system of linear equations and solution of linear equations in two or three variables using inverse of a matrix.

Determinant

To every square matrix $A=[a _{i j}]$ of order $n$, we can associate a number (real or complex) called determinant of the square matrix A, where $a _{i j}=(i, j)^{\text{th }}$ element of A.

This may be thought of as a function which associates each square matrix with a unique number (real or complex). If $M$ is the set of square matrices, $K$ is the set of numbers (real or complex) and $f: M \to K$ is defined by $f(A)=k$, where $A \in M$ and $k \in K$, then $f(A)$ is called the determinant of $A$. It is also denoted by $|A|$ or $det A$ or $\Delta$.

$ \text{ If } A=\begin{vmatrix} a & b \\ c & d \end{vmatrix} \text{, then determinant of } A \text{ is written as }|A|=\begin{vmatrix} a & b \\ c & d \end{vmatrix}=det(A) $

Remarks

(i) For matrix A, $|A|$ is read as determinant of $A$ and not modulus of $A$.

(ii) Only square matrices have determinants.

Determinant of a matrix of order one

Let $A=[a]$ be the matrix of order 1, then determinant of $A$ is defined to be equal to $a$

Determinant of a matrix of order two

Let

$ A=\begin{vmatrix} a _{11} & a _{12} \\ a _{21} & a _{22} \end{vmatrix} \text{ be a matrix of order } 2 \times 2, $

then the determinant of $A$ is defined as:

$ det(A)=|A|=\Delta=\begin{vmatrix} a _{11} & & a _{12} \\ a _{21} & & a _{22} \end{vmatrix}=a _{11} a _{22}-a _{21} a _{12} $

Example 1 Evaluate $\begin{vmatrix}2 & 4 \\ -1 & 2\end{vmatrix}$.

Solution We have $\begin{vmatrix}2 & 4 \\ -1 & 2\end{vmatrix}=2(2)-4(-1)=4+4=8$.

Example 2 Evaluate $\begin{vmatrix}x & x+1 \\ x-1 & x\end{vmatrix}$

Solution We have

$ \begin{vmatrix} x & x+1 \\ x-1 & x \end{vmatrix}=x(x)-(x+1)(x-1)=x^{2}-(x^{2}-1)=x^{2}-x^{2}+1=1 $

Determinant of a matrix of order $3 \times 3$

Determinant of a matrix of order three can be determined by expressing it in terms of second order determinants. This is known as expansion of a determinant along a row (or a column). There are six ways of expanding a determinant of order

3 corresponding to each of three rows $(R_1, R_2.$ and $.R_3)$ and three columns $(C_1, C_2.$ and $C_3)$ giving the same value as shown below.

Consider the determinant of square matrix $A=[a _{i j}] _{3 \times 3}$

i.e.,

$ |A|=\begin{vmatrix} a _{11} & a _{12} & a _{13} \\ a _{21} & a _{22} & a _{23} \\ a _{31} & a _{32} & a _{33} \end{vmatrix} $

Expansion along first Row $(\mathbf{R} _1)$

Step 1 Multiply first element $ a _ {11}$ of $\mathbf{R} _ {1}$ by $(-1)^{(1+1)}[(-1)^{.\text{sum of suffixes in } a _ {11}}.$ and with the second order determinant obtained by deleting the elements of first row $(R_1)$ and first column $(C _ {1})$ of $|A|$ as $a _ {11}$ lies in $ R _ {1} $ and $ C _ {1} $,

i.e.,

$ (-1)^{1+1} a _{11}\begin{vmatrix} a _{22} & a _{23} \\ a _{32} & a _{33} \end{vmatrix} $

Step 2 Multiply 2 nd element $a _{12}$ of $R_1$ by $(-1)^{1+2}[(-1)^{\text{sum of suffixes in } a _{12}}]$ and the second order determinant obtained by deleting elements of first row $(R_1)$ and 2 nd column $(C_2)$ of $|A|$ as $a _{12}$ lies in $R_1$ and $C_2$,

i.e., $\quad(-1)^{1+2} a _{12}\begin{vmatrix}a _{21} & a _{23} \\ a _{31} & a _{33}\end{vmatrix}$

Step 3 Multiply third element $a _{13}$ of $R_1$ by $(-1)^{1+3}[(-1)^{\text{sum of suffixes in } a _{13}}]$ and the second order determinant obtained by deleting elements of first row $(R_1)$ and third column $(C_3)$ of $|A|$ as $a _{13}$ lies in $R_1$ and $C_3$,

i.e., $\quad(-1)^{1+3} a _{13}\begin{vmatrix}a _{21} & a _{22} \\ a _{31} & a _{32}\end{vmatrix}$

Step 4 Now the expansion of determinant of A, that is, $|A|$ written as sum of all three terms obtained in steps 1,2 and 3 above is given by

$ \begin{aligned} det A= & |A|=(-1)^{1+1} a _{11}\begin{vmatrix} a _{22} & a _{23} \\ a _{32} & a _{33} \end{vmatrix}+(-1)^{1+2} a _{12}\begin{vmatrix} a _{21} & a _{23} \\ a _{31} & a _{33} \end{vmatrix} \\ & +(-1)^{1+3} a _{13}\begin{vmatrix} a _{21} & a _{22} \\ a _{31} & a _{32} \end{vmatrix} \\ |A|= & a _{11}(a _{22} a _{33}-a _{32} a _{23})-a _{12}(a _{21} a _{33}-a _{31} a _{23}) \\ & +a _{13}(a _{21} a _{32}-a _{31} a _{22}) \end{aligned} $

or

$ \begin{aligned} |A|= & a _{11} a _{22} a _{33}-a _{11} a _{32} a _{23}-a _{12} a _{21} a _{33}+a _{12} a _{31} a _{23}+a _{13} a _{21} a _{32} \\ & -a _{13} a _{31} a _{22} \end{aligned} $

Note We shall apply all four steps together.

Expansion along second row $(\mathbf{R} _2)$

$ |A|=\begin{vmatrix} a_ {11} & a_ {12} & a_ {13} \\ a_ {21} & a_ {22} & a_ {23} \\ a_ {31} & a_ {32} & a_ {33} \end{vmatrix} $

Expanding along $R_2$, we get

$ \begin{aligned} |A|= & (-1)^{2+1} a _{21}\begin{vmatrix} a _{12} & a _{13} \\ a _{32} & a _{33} \end{vmatrix}+(-1)^{2+2} a _{22}\begin{vmatrix} a _{11} & a _{13} \\ a _{31} & a _{33} \end{vmatrix} \\ & +(-1)^{2+3} a _{23}\begin{vmatrix} a _{11} & a _{12} \\ a _{31} & a _{32} \end{vmatrix} \\ = & -a _{21}(a _{12} a _{33}-a _{32} a _{13})+a _{22}(a _{11} a _{33}-a _{31} a _{13}) \\ & -a _{23}(a _{11} a _{32}-a _{31} a _{12}) \\ |A|= & -a _{21} a _{12} a _{33}+a _{21} a _{32} a _{13}+a _{22} a _{11} a _{33}-a _{22} a _{31} a _{13}-a _{23} a _{11} a _{32} \\ & +a _{23} a _{31} a _{12} \\ = & a _{11} a _{22} a _{33}-a _{11} a _{23} a _{32}-a _{12} a _{21} a _{33}+a _{12} a _{23} a _{31}+a _{13} a _{21} a _{32} \\ & -a _{13} a _{31} a _{22} \end{aligned} $

Expansion along first Column $(C_1)$

$ |A|=\begin{vmatrix} a _{11} & a _{12} & a _{13} \\ a _{21} & a _{22} & a _{23} \\ a _{31} & a _{32} & a _{33} \end{vmatrix} $

By expanding along $C_1$, we get

$ \begin{aligned} |A|= & a _{11}(-1)^{1+1}\begin{vmatrix} a _{22} & a _{23} \\ a _{32} & a _{33} \end{vmatrix}+a _{21}(-1)^{2+1}\begin{vmatrix} a _{12} & a _{13} \\ a _{32} & a _{33} \end{vmatrix} \\ & +a _{31}(-1)^{3+1}\begin{vmatrix} a _{12} & a _{13} \\ a _{22} & a _{23} \end{vmatrix} \\ = & a _{11}(a _{22} a _{33}-a _{23} a _{32})-a _{21}(a _{12} a _{33}-a _{13} a _{32})+a _{31}(a _{12} a _{23}-a _{13} a _{22}) \end{aligned} $

$ \begin{aligned} |A|= & a _{11} a _{22} a _{33}-a _{11} a _{23} a _{32}-a _{21} a _{12} a _{33}+a _{21} a _{13} a _{32}+a _{31} a _{12} a _{23} \\ & -a _{31} a _{13} a _{22} \\ = & a _{11} a _{22} a _{33}-a _{11} a _{23} a _{32}-a _{12} a _{21} a _{33}+a _{12} a _{23} a _{31}+a _{13} a _{21} a _{32} \\ & -a _{13} a _{31} a _{22} \end{aligned} $

Clearly, values of $|A|$ in (1), (2) and (3) are equal. It is left as an exercise to the reader to verify that the values of $|A|$ by expanding along $R_3, C_2$ and $C_3$ are equal to the value of $|A|$ obtained in (1), (2) or (3).

Hence, expanding a determinant along any row or column gives same value.

Remarks

(i) For easier calculations, we shall expand the determinant along that row or column which contains maximum number of zeros.

(ii) While expanding, instead of multiplying by $(-1)^{i+j}$, we can multiply by +1 or -1 according as $(i+j)$ is even or odd.

(iii) Let $A=\begin{vmatrix}2 & 2 \\ 4 & 0\end{vmatrix}$ and $B=\begin{vmatrix}1 & 1 \\ 2 & 0\end{vmatrix}$. Then, it is easy to verify that $A=2 B$. Also $|A|=0-8=-8$ and $|B|=0-2=-2$.

Observe that, $|A|=4(-2)=2^{2}|B|$ or $|A|=2^{n}|B|$, where $n=2$ is the order of square matrices $A$ and $B$.

In general, if $A=k B$ where $A$ and $B$ are square matrices of order $n$, then $|A|=k^{n}$ $|B|$, where $n=1,2,3$

Example 3 Evaluate the determinant $\Delta=\begin{vmatrix}1 & 2 & 4 \\ -1 & 3 & 0 \\ 4 & 1 & 0\end{vmatrix}$.

Solution Note that in the third column, two entries are zero. So expanding along third column $(C_3)$, we get

$ \begin{aligned} \Delta & =4\begin{vmatrix} -1 & 3 \\ 4 & 1 \end{vmatrix}-0\begin{vmatrix} 1 & 2 \\ 4 & 1 \end{vmatrix}+0\begin{vmatrix} 1 & 2 \\ -1 & 3 \end{vmatrix} \\ & =4(-1-12)-0+0=-52 \end{aligned} $

Example 4 Evaluate $\Delta=\begin{vmatrix}0 & \sin \alpha & -\cos \alpha \\ -\sin \alpha & 0 & \sin \beta \\ \cos \alpha & -\sin \beta & 0\end{vmatrix}$

Solution Expanding along $R_1$, we get

$ \begin{aligned} \Delta & =0\begin{vmatrix} 0 & \sin \beta \\ -\sin \beta & 0 \end{vmatrix}-\sin \alpha\begin{vmatrix} -\sin \alpha & \sin \beta \\ \cos \alpha & 0 \end{vmatrix}-\cos \alpha\begin{vmatrix} -\sin \alpha & 0 \\ \cos \alpha & -\sin \beta \end{vmatrix} \\ & =0-\sin \alpha(0-\sin \beta \cos \alpha)-\cos \alpha(\sin \alpha \sin \beta-0) \\ & =\sin \alpha \sin \beta \cos \alpha-\cos \alpha \sin \alpha \sin \beta=0 \end{aligned} $

Example 5 Find values of $x$ for which $\begin{vmatrix}3 & x \\ x & 1\end{vmatrix}=\begin{vmatrix}3 & 2 \\ 4 & 1\end{vmatrix}$.

Solution We have $\begin{vmatrix}3 & x \\ x & 1\end{vmatrix}=\begin{vmatrix}3 & 2 \\ 4 & 1\end{vmatrix}$

i.e.

$ 3-x^{2}=3-8 $

i.e.

$ x^{2}=8 $

Hence

$ x= \pm 2 \sqrt{2} $

EXERCISE 4.1

Evaluate the determinants in Exercises 1 and 2.

1. $\begin{vmatrix}2 & 4 \\ -5 & -1\end{vmatrix}$

Solution

$ \begin{vmatrix} 2 & 4 \\ -5 & -1 \end{vmatrix} =2(-1)-4(-5)=-2+20=18 $

2. (i) $\begin{vmatrix}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta\end{vmatrix} \quad\quad $(ii) $\begin{vmatrix}x^{2}-x+1 & x-1 \\ x+1 & x+1\end{vmatrix}$

Solution

(i) $ \begin{vmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta\end{vmatrix} =(\cos \theta)(\cos \theta)-(-\sin \theta)(\sin \theta)=\cos ^{2} \theta+\sin ^{2} \theta=1$

(ii) $ \begin{vmatrix} x^{2}-x+1 & x-1 \\ x+1 & x+1\end{vmatrix} $

$=(x^{2}-x+1)(x+1)-(x-1)(x+1)$

$=x^{3}-x^{2}+x+x^{2}-x+1-(x^{2}-1)$

$=x^{3}+1-x^{2}+1$

$=x^{3}-x^{2}+2$

3. If $A=\begin{vmatrix}1 & 2 \\ 4 & 2\end{vmatrix}$, then show that $|2 A|=4|A|$

Solution

The given matrix is $A= \begin{vmatrix} 1 & 2 \\ 4 & 2 \end{vmatrix} $.

$\therefore 2 A=2 \begin{vmatrix} 1 & 2 \\ 4 & 2 \end{vmatrix} = \begin{vmatrix} 2 & 4 \\ 8 & 4 \end{vmatrix} $

$\therefore$ L.H.S. $=|2 A|= \begin{vmatrix} 2 & 4 \\ 8 & 4\end{vmatrix} =2 \times 4-4 \times 8=8-32=-24$

Now, $|A|= \begin{vmatrix} 1 & 2 \\ 4 & 2\end{vmatrix} =1 \times 2-2 \times 4=2-8=-6$

$\therefore$ R.H.S. $=4|A|=4 \times(-6)=-24$

$\therefore$ L.H.S. $=$ R.H.S.

4. If $A=\begin{vmatrix}1 & 0 & 1 \\ 0 & 1 & 2 \\ 0 & 0 & 4\end{vmatrix}$, then show that $|3 A|=27|A|$

Solution

The given matrix is $A= \begin{vmatrix} 1 & 0 & 1 \\ 0 & 1 & 2 \\ 0 & 0 & 4 \end{vmatrix} $

It can be observed that in the first column, two entries are zero. Thus, we expand along the first column $(C_1.$ ) for easier calculation.

$$ \begin{align*} & |A|=1 \begin{vmatrix} 1 & 2 \\ 0 & 4 \end{vmatrix} -0 \begin{vmatrix} 0 & 1 \\ 0 & 4 \end{vmatrix} +0 \begin{vmatrix} 0 & 1 \\ 1 & 2 \end{vmatrix} =1(4-0)-0+0=4 \\ & \therefore 27|A|=27(4)=108 \tag{i}\\ & \text{ Now, } 3 A=3 \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 2 \\ 0 & 0 & 4 \end{bmatrix} = \begin{bmatrix} 3 & 0 & 3 \\ 0 & 3 & 6 \\ 0 & 0 & 12 \end{bmatrix} \\ & \begin{align*} & \ldots A \mid=3 \begin{vmatrix} 3 & 6 \\ 0 & 12 \end{vmatrix} -0 \begin{vmatrix} 0 & 3 \\ 0 & 12 \end{vmatrix} +0 \begin{vmatrix} 0 & 3 \\ 3 & 6 \end{vmatrix} \\ & \quad=3(36-0)=3(36)=108 \end{align*} \end{align*} $$

From equations (i) and (ii), we have:

$|3 A|=27|A|$

Hence, the given result is proved.

5. Evaluate the determinants

(i) $\begin{vmatrix}3 & -1 & -2 \\ 0 & 0 & -1 \\ 3 & -5 & 0\end{vmatrix}\quad\quad \quad\quad$ (ii) $\begin{vmatrix}3 & -4 & 5 \\ 1 & 1 & -2 \\ 2 & 3 & 1\end{vmatrix}$

(iii) $\begin{vmatrix}0 & 1 & 2 \\ -1 & 0 & -3 \\ -2 & 3 & 0\end{vmatrix}\quad\quad \quad\quad$ (iv) $\begin{vmatrix}2 & -1 & -2 \\ 0 & 2 & -1 \\ 3 & -5 & 0\end{vmatrix}$

Solution

(i) Let $A= \begin{vmatrix} 3 & -1 & -2 \\ 0 & 0 & -1 \\ 3 & -5 & 0\end{vmatrix} $.

It can be observed that in the second row, two entries are zero. Thus, we expand along the second row for easier calculation.

$|A|=-0 \begin{vmatrix} -1 & -2 \\ -5 & 0\end{vmatrix} +0 \begin{vmatrix} 3 & -2 \\ 3 & 0\end{vmatrix} -(-1) \begin{vmatrix} 3 & -1 \\ 3 & -5\end{vmatrix} =(-15+3)=-12$

(ii) Let $A= \begin{cases} 3 & -4 & 5 \\ 1 & 1 & -2 \\ 2 & 3 & 1 \end{cases} $.

By expanding along the first row, we have:

$ \begin{aligned} |A| & =3 \begin{vmatrix} 1 & -2 \\ 3 & 1 \end{vmatrix} +4 \begin{vmatrix} 1 & -2 \\ 2 & 1 \end{vmatrix} +5 \begin{vmatrix} 1 & 1 \\ 2 & 3 \end{vmatrix} \\ & =3(1+6)+4(1+4)+5(3-2) \\ & =3(7)+4(5)+5(1) \\ & =21+20+5=46 \end{aligned} $

(iii) Let $A= \begin{cases} 0 & 1 & 2 \\ -1 & 0 & -3 \\ -2 & 3 & 0 \end{cases} $.

By expanding along the first row, we have:

$ \begin{aligned} |A| & =0 \begin{vmatrix} 0 & -3 \\ 3 & 0 \end{vmatrix} -1 \begin{vmatrix} -1 & -3 \\ -2 & 0 \end{vmatrix} +2 \begin{vmatrix} -1 & 0 \\ -2 & 3 \end{vmatrix} \\ & =0-1(0-6)+2(-3-0) \\ & =-1(-6)+2(-3) \\ & =6-6=0 \end{aligned} $

(iv) Let $A= \begin{cases} 2 & -1 & -2 \\ 0 & 2 & -1 \\ 3 & -5 & 0 \end{cases} $.

By expanding along the first column, we have:

$ \begin{aligned} |A| & =2 \begin{vmatrix} 2 & -1 \\ -5 & 0 \end{vmatrix} -0 \begin{vmatrix} -1 & -2 \\ -5 & 0 \end{vmatrix} +3 \begin{vmatrix} -1 & -2 \\ 2 & -1 \end{vmatrix} \\ & =2(0-5)-0+3(1+4) \\ & =-10+15=5 \end{aligned} $

6. If $A=\begin{vmatrix}1 & 1 & -2 \\ 2 & 1 & -3 \\ 5 & 4 & -9\end{vmatrix}$, find $|A|$

Solution

Let $A= \begin{cases} 1 & 1 & -2 \\ 2 & 1 & -3 \\ 5 & 4 & -9 \end{cases} $.

By expanding along the first row, we have:

$ \begin{aligned} |A| & =1 \begin{vmatrix} 1 & -3 \\ 4 & -9 \end{vmatrix} -1 \begin{vmatrix} 2 & -3 \\ 5 & -9 \end{vmatrix} -2 \begin{vmatrix} 2 & 1 \\ 5 & 4 \end{vmatrix} \\ & =1(-9+12)-1(-18+15)-2(8-5) \\ & =1(3)-1(-3)-2(3) \\ & =3+3-6 \\ & =6-6 \\ & =0 \end{aligned} $

7. Find values of $x$, if

(i) $\begin{vmatrix}2 & 4 \\ 5 & 1\end{vmatrix}=\begin{vmatrix}2 x & 4 \\ 6 & x\end{vmatrix}\quad\quad \quad\quad$ (ii) $\begin{vmatrix}2 & 3 \\ 4 & 5\end{vmatrix}=\begin{vmatrix}x & 3 \\ 2 x & 5\end{vmatrix}$

Solution

(i) $ \begin{vmatrix} 2 & 4 \\ 5 & 1\end{vmatrix} = \begin{vmatrix} 2 x & 4 \\ 6 & x\end{vmatrix} $

$\Rightarrow 2 \times 1-5 \times 4=2 x \times x-6 \times 4$

$\Rightarrow 2-20=2 x^{2}-24$

$\Rightarrow 2 x^{2}=6$

$\Rightarrow x^{2}=3$

$\Rightarrow x= \pm \sqrt{3}$

(ii) $ \begin{vmatrix} 2 & 3 \\ 4 & 5\end{vmatrix} = \begin{vmatrix} x & 3 \\ 2 x & 5\end{vmatrix} $

$\Rightarrow 2 \times 5-3 \times 4=x \times 5-3 \times 2 x$

$\Rightarrow 10-12=5 x-6 x$

$\Rightarrow-2=-x$

$\Rightarrow x=2$

8. If $\begin{vmatrix}x & 2 \\ 18 & x\end{vmatrix}=\begin{vmatrix}6 & 2 \\ 18 & 6\end{vmatrix}$, then $x$ is equal to

(A) 6 prope(B) $\pm 6$ (C) -6 (D) 0

Solution

$ \begin{vmatrix} x & 2 \\ 18 & x\end{vmatrix} = \begin{vmatrix} 6 & 2 \\ 18 & 6\end{vmatrix} $

$\Rightarrow x^{2}-36=36-36$

$\Rightarrow x^{2}-36=0$

$\Rightarrow x^{2}=36$

$\Rightarrow x= \pm 6$

Hence, the correct answer is B.

3. Properties of Determinants

In the previous section, we have learnt how to expand the determinants. In this section, we will study some properties of determinants which simplifies its evaluation by obtaining maximum number of zeros in a row or a column. These properties are true for determinants of any order. However, we shall restrict ourselves upto determinants of order 3 only.

Property 1 The value of the determinant remains unchanged if its rows and columns are interchanged.

Verification Let $\Delta=\left|\begin{array}{lll}a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3\end{array}\right|$ Expanding along first row, we get $$ \begin{aligned} \Delta & =a_1\left|\begin{array}{ll} b_2 & b_3 \\ c_2 & c_3 \end{array}\right|-a_2\left|\begin{array}{ll} b_1 & b_3 \\ c_1 & c_3 \end{array}\right|+a_3\left|\begin{array}{ll} b_1 & b_2 \\ c_1 & c_2 \end{array}\right| \\ & =a_1\left(b_2 c_3-b_3 c_2\right)-a_2\left(b_1 c_3-b_3 c_1\right)+a_3\left(b_1 c_2-b_2 c_1\right) \end{aligned} $$

By interchanging the rows and columns of $\Delta$, we get the determinant $$ \Delta_1=\left|\begin{array}{lll} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{array}\right| $$

Expanding $\Delta_1$ along first column, we get $$ \Delta_1=a_1\left(b_2 c_3-c_2 b_3\right)-a_2\left(b_1 c_3-b_3 c_1\right)+a_3\left(b_1 c_2-b_2 c_1\right) $$

Hence $\Delta=\Delta_1$ Remark It follows from above property that if $\mathrm{A}$ is a square matrix, then $\operatorname{det}(A)=\operatorname{det}\left(A^{\prime}\right)$, where $A^{\prime}=$ transpose of $A$.

Note If $\mathrm{R}_i=i$ th row and $\mathrm{C}_i=i$ th column, then for interchange of row and columns, we will symbolically write $\mathrm{C}_i \leftrightarrow \mathrm{R}_i$ Let us verify the above property by example.

Example 6 Verify Property 1 for $\Delta=\left|\begin{array}{ccc}2 & -3 & 5 \\ 6 & 0 & 4 \\ 1 & 5 & -7\end{array}\right|$

Solution Expanding the determinant along first row, we have $$ \begin{aligned} \Delta & =2\left|\begin{array}{rr} 0 & 4 \\ 5 & -7 \end{array}\right|-(-3)\left|\begin{array}{rr} 6 & 4 \\ 1 & -7 \end{array}\right|+5\left|\begin{array}{ll} 6 & 0 \\ 1 & 5 \end{array}\right| \\ & =2(0-20)+3(-42-4)+5(30-0) \\ & =-40-138+150=-28 \end{aligned} $$

By interchanging rows and columns, we get $$ \Delta_1=\left|\begin{array}{rrr} 2 & 6 & 1 \\ -3 & 0 & 5 \\ 5 & 4 & -7 \end{array}\right| $$ (Expanding along first column)

$$ \begin{aligned} & =2\left|\begin{array}{rr} 0 & 5 \ 4 & -7 \end{array}\right|-(-3)\left|\begin{array}{rr} 6 & 1 \\ 4 & -7 \end{array}\right|+5\left|\begin{array}{ll} 6 & 1 \\ 0 & 5 \end{array}\right| \\ & =2(0-20)+3(-42-4)+5(30-0) \\ & =-40-138+150=-28 \end{aligned} $$

Clearly $\Delta=\Delta_1$ Hence, Property 1 is verified. Property 2 If any two rows (or columns) of a determinant are interchanged, then sign of determinant changes. Verification Let $\Delta=\left|\begin{array}{lll}a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3\end{array}\right|$

Expanding along first row, we get $$ \Delta=a_1\left(b_2 c_3-b_3 c_2\right)-a_2\left(b_1 c_3-b_3 c_1\right)+a_3\left(b_1 c_2-b_2 c_1\right) $$

Interchanging first and third rows, the new determinant obtained is given by $$ \Delta_1=\left|\begin{array}{lll} c_1 & c_2 & c_3 \\ b_1 & b_2 & b_3 \\ a_1 & a_2 & a_3 \end{array}\right| $$

Expanding along third row, we get $$ \begin{aligned} \Delta_1 & =a_1\left(c_2 b_3-b_2 c_3\right)-a_2\left(c_1 b_3-c_3 b_1\right)+a_3\left(b_2 c_1-b_1 c_2\right) \\ & =-\left[a_1\left(b_2 c_3-b_3 c_2\right)-a_2\left(b_1 c_3-b_3 c_1\right)+a_3\left(b_1 c_2-b_2 c_1\right)\right] \end{aligned} $$

Clearly $\Delta_1=-\Delta$ Similarly, we can verify the result by interchanging any two columns. Note We can denote the interchange of rows by $\mathrm{R}_i \leftrightarrow \mathrm{R}_j$ and interchange of columns by $\mathrm{C}_i \leftrightarrow \mathrm{C}_j$.

Example 7 Verify Property 2 for $\Delta=\left|\begin{array}{rrr}2 & -3 & 5 \ 6 & 0 & 4 \ 1 & 5 & -7\end{array}\right|$.

Solution $\Delta=\left|\begin{array}{rrr}2 & -3 & 5 \\ 6 & 0 & 4 \\ 1 & 5 & -7\end{array}\right|=-28$

(See Example 6)

Interchanging rows $R_2$ and $R_3$ i.e., $R_2 \leftrightarrow R_3$, we have $$ \Delta_1=\left|\begin{array}{rrr} 2 & -3 & 5 \\ 1 & 5 & -7 \\ 6 & 0 & 4 \end{array}\right| $$

Expanding the determinant $\Delta_1$ along first row, we have $$ \begin{aligned} \Delta_1 & =2\left|\begin{array}{rr} 5 & -7 \\ 0 & 4 \end{array}\right|-(-3)\left|\begin{array}{rr} 1 & -7 \\ 6 & 4 \end{array}\right|+5\left|\begin{array}{ll} 1 & 5 \\ 6 & 0 \end{array}\right| \\ & =2(20-0)+3(4+42)+5(0-30) \\ & =40+138-150=28 \end{aligned} $$

Clearly $$ \Delta_1=-\Delta $$

Hence, Property 2 is verified. Property 3 If any two rows (or columns) of a determinant are identical (all corresponding elements are same), then value of determinant is zero. Proof If we interchange the identical rows (or columns) of the determinant $\Delta$, then $\Delta$ does not change. However, by Property 2, it follows that $\Delta$ has changed its sign Therefore $$ \begin{aligned} & \Delta=-\Delta \\ & \Delta=0 \end{aligned} $$ or Let us verify the above property by an example.

Example 8 Evaluate $\Delta=\left|\begin{array}{lll}3 & 2 & 3 \\ 2 & 2 & 3 \\ 3 & 2 & 3\end{array}\right|$

Solution Expanding along first row, we get $$ \begin{aligned} \Delta & =3(6-6)-2(6-9)+3(4-6) \\ & =0-2(-3)+3(-2)=6-6=0 \end{aligned} $$

Here $\mathrm{R}_1$ and $\mathrm{R}_3$ are identical. Property 4 If each element of a row (or a column) of a determinant is multiplied by a constant $k$, then its value gets multiplied by $k$

Verification Let $\Delta=\left|\begin{array}{lll}a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3\end{array}\right|$ and $\Delta_1$ be the determinant obtained by multiplying the elements of the first row by $k$. Then $$ \Delta_1=\left|\begin{array}{ccc} k a_1 & k b_1 & k c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{array}\right| $$

Expanding along first row, we get $$ \begin{aligned} \Delta_1 & =k a_1\left(b_2 c_3-b_3 c_2\right)-k b_1\left(a_2 c_3-c_2 a_3\right)+k c_1\left(a_2 b_3-b_2 a_3\right) \\ & =k\left[a_1\left(b_2 c_3-b_3 c_2\right)-b_1\left(a_2 c_3-c_2 a_3\right)+c_1\left(a_2 b_3-b_2 a_3\right)\right] \\ & =k \Delta \end{aligned} $$

Hence $$ \left|\begin{array}{ccc} k a_1 & k b_1 & k c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{array}\right|=k\left|\begin{array}{lll} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{array}\right| $$

Remarks (i) By this property, we can take out any common factor from any one row or any one column of a given determinant.

(ii) If corresponding elements of any two rows (or columns) of a determinant are proportional (in the same ratio), then its value is zero. For example $\Delta=\left|\begin{array}{ccc}a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ k a_1 & k a_2 & k a_3\end{array}\right|=0$ (rows $\mathrm{R}_1$ and $\mathrm{R}_2$ are proportional)

Example 9 Evaluate $\left|\begin{array}{ccc}102 & 18 & 36 \\ 1 & 3 & 4 \\ 17 & 3 & 6\end{array}\right|$

Solution Note that $\left|\begin{array}{ccc}102 & 18 & 36 \\ 1 & 3 & 4 \\ 17 & 3 & 6\end{array}\right|=\left|\begin{array}{ccc}6(17) & 6(3) & 6(6) \\ 1 & 3 & 4 \\ 17 & 3 & 6\end{array}\right|=6\left|\begin{array}{ccc}17 & 3 & 6 \\ 1 & 3 & 4 \\ 17 & 3 & 6\end{array}\right|=0$

(Using Properties 3 and 4) Property 5 If some or all elements of a row or column of a determinant are expressed as sum of two (or more) terms, then the determinant can be expressed as sum of two (or more) determinants.

For example, $\left|\begin{array}{ccc}a_1+\lambda_1 & a_2+\lambda_2 & a_3+\lambda_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3\end{array}\right|=\left|\begin{array}{ccc}a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3\end{array}\right|+\left|\begin{array}{ccc}\lambda_1 & \lambda_2 & \lambda_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3\end{array}\right|$ Verification L.H.S. $=\left|\begin{array}{ccc}a_1+\lambda_1 & a_2+\lambda_2 & a_3+\lambda_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3\end{array}\right|$

Expanding the determinants along the first row, we get $$ \begin{aligned} \Delta= & \left(a_1+\lambda_1\right)\left(b_2 c_3-c_2 b_3\right)-\left(a_2+\lambda_2\right)\left(b_1 c_3-b_3 c_1\right) \\ & +\left(a_3+\lambda_3\right)\left(b_1 c_2-b_2 c_1\right) \\ = & a_1\left(b_2 c_3-c_2 b_3\right)-a_2\left(b_1 c_3-b_3 c_1\right)+a_3\left(b_1 c_2-b_2 c_1\right) \\ & +\lambda_1\left(b_2 c_3-c_2 b_3\right)-\lambda_2\left(b_1 c_3-b_3 c_1\right)+\lambda_3\left(b_1 c_2-b_2 c_1\right) \end{aligned} $$ (by rearranging terms) $$ =\left|\begin{array}{lll} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{array}\right|+\left|\begin{array}{ccc} \lambda_1 & \lambda_2 & \lambda_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{array}\right|=\text { R.H.S. } $$

Similarly, we may verify Property 5 for other rows or columns.

Example 10 Show that $\left|\begin{array}{ccc}a & b & c \\ a+2 x & b+2 y & c+2 z \\ x & y & z\end{array}\right|=0$

Solution We have $\left|\begin{array}{ccc}a & b & c \\ a+2 x & b+2 y & c+2 z \\ x & y & z\end{array}\right|=\left|\begin{array}{ccc}a & b & c \\ a & b & c \\ x & y & z\end{array}\right|+\left|\begin{array}{ccc}a & b & c \\ 2 x & 2 y & 2 z \\ x & y & z\end{array}\right|$ (by Property 5) $=0+0=0$ (Using Property 3 and Property 4)

Property 6 If, to each element of any row or column of a determinant, the equimultiples of corresponding elements of other row (or column) are added, then value of determinant remains the same, i.e., the value of determinant remain same if we apply the operation $\mathrm{R}_i \rightarrow \mathrm{R}_i+k \mathrm{R}_j$ or $\mathrm{C}_i \rightarrow \mathrm{C}_i+k \mathrm{C}_j$. Verification

Let $$ \Delta=\left|\begin{array}{lll} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{array}\right| \text { and } \Delta_1=\left|\begin{array}{ccc} a_1+k c_1 & a_2+k c_2 & a_3+k c_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{array}\right| \text {, } $$ where $\Delta_1$ is obtained by the operation $\mathrm{R}_1 \rightarrow \mathrm{R}_1+k \mathrm{R}_3$. Here, we have multiplied the elements of the third row $\left(\mathrm{R}_3\right)$ by a constant $k$ and added them to the corresponding elements of the first row $\left(\mathrm{R}_1\right)$. Symbolically, we write this operation as $\mathrm{R}_1 \rightarrow \mathrm{R}_1+k \mathrm{R}_3$.

Now, again $$ \begin{aligned} & \Delta_1=\left|\begin{array}{lll} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{array}\right|+\left|\begin{array}{ccc} k c_1 & k c_2 & k c_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{array}\right| \text { (Using Property 5) } \\ & =\Delta+0 \\ & (\text { since } \mathrm{R}_1 \text { and } \mathrm{R}_3 \text { are proportional }) \\ & \end{aligned} $$

Hence $\Delta=\Delta_1$ Remarks (i) If $\Delta_1$ is the determinant obtained by applying $\mathrm{R}_i \rightarrow k \mathrm{R}_i$ or $\mathrm{C}_i \rightarrow k \mathrm{C}_i$ to the determinant $\Delta$, then $\Delta_1=k \Delta$. (ii) If more than one operation like $\mathrm{R}_i \rightarrow \mathrm{R}_i+k \mathrm{R}_j$ is done in one step, care should be taken to see that a row that is affected in one operation should not be used in another operation. A similar remark applies to column operations.

Example 11 Prove that $\left|\begin{array}{ccc}a & a+b & a+b+c \\ 2 a & 3 a+2 b & 4 a+3 b+2 c \\ 3 a & 6 a+3 b & 10 a+6 b+3 c\end{array}\right|=a^3$.

Solution Applying operations $\mathrm{R}_2 \rightarrow \mathrm{R}_2-2 \mathrm{R}_1$ and $\mathrm{R}_3 \rightarrow \mathrm{R}_3-3 \mathrm{R}_1$ to the given determinant $\Delta$, we have $$ \Delta=\left|\begin{array}{ccc} a & a+b & a+b+c \\ 0 & a & 2 a+b \\ 0 & 3 a & 7 a+3 b \end{array}\right| $$

Now applying $R_3 \rightarrow R_3-3 R_2$, we get $$ \Delta=\left|\begin{array}{ccc} a & a+b & a+b+c \\ 0 & a & 2 a+b \\ 0 & 0 & a \end{array}\right| $$

Expanding along $\mathrm{C}_1$, we obtain $$ \begin{aligned} \Delta & =a\left|\begin{array}{cc} a & 2 a+b \\ 0 & a \end{array}\right|+0+0 \\ & =a\left(a^2-0\right)=a\left(a^2\right)=a^3 \end{aligned} $$

Example 12 Without expanding, prove that $$ \Delta=\left|\begin{array}{ccc} x+y & y+z & z+x \\ z & x & y \\ 1 & 1 & 1 \end{array}\right|=0 $$

Solution Applying $\mathrm{R}_1 \rightarrow \mathrm{R}_1+\mathrm{R}_2$ to $\Delta$, we get $$ \Delta=\left|\begin{array}{ccc} x+y+z & x+y+z & x+y+z \\ z & x & y \\ 1 & 1 & 1 \end{array}\right| $$

Since the elements of $\mathrm{R}_1$ and $\mathrm{R}_3$ are proportional, $\Delta=0$.

Example 13 Evaluate $$ \Delta=\left|\begin{array}{lll} 1 & a & b c \\ 1 & b & c a \\ 1 & c & a b \end{array}\right| $$

Solution Applying $\mathrm{R}_2 \rightarrow \mathrm{R}_2-\mathrm{R}_1$ and $\mathrm{R}_3 \rightarrow \mathrm{R}_3-\mathrm{R}_1$, we get $$ \Delta=\left|\begin{array}{ccc} 1 & a & b c \\ 0 & b-a & c(a-b) \\ 0 & c-a & b(a-c) \end{array}\right| $$

Taking factors $(b-a)$ and $(c-a)$ common from $\mathrm{R}_2$ and $\mathrm{R}_3$, respectively, we get $$ \begin{aligned} & \Delta=(b-a)(c-a)\left|\begin{array}{lll} 1 & a & b c \\ 0 & 1 & -c \\ 0 & 1 & -b \end{array}\right| \\ & =(b-a)(c-a)[(-b+c)] \text { (Expanding along first column) } \\ & =(a-b)(b-c)(c-a) \\ & \text { Example } 14 \text { Prove that }\left|\begin{array}{ccc} b+c & a & a \\ b & c+a & b \\ c & c & a+b \end{array}\right|=4 a b c \\ & \end{aligned} $$ $$ \text { Solution Let } \Delta=\left|\begin{array}{ccc} b+c & a & a \\ b & c+a & b \\ c & c & a+b \end{array}\right| $$

Applying $\quad \mathrm{R}_1 \rightarrow \mathrm{R}_1-\mathrm{R}_2-\mathrm{R}_3$ to $\Delta$, we get $$ \Delta=\left|\begin{array}{ccc} 0 & -2 c & -2 b \\ b & c+a & b \\ c & c & a+b \end{array}\right| $$

Expanding along $\mathrm{R}_1$, we obtain $$ \begin{aligned} \Delta & =0\left|\begin{array}{cc} c+a & b \\ c & a+b \end{array}\right|-(-2 c)\left|\begin{array}{cc} b & b \\ c & a+b \end{array}\right|+(-2 b)\left|\begin{array}{cc} b & c+a \\ c & c \end{array}\right| \\ & =2 c\left(a b+b^2-b c\right)-2 b\left(b c-c^2-a c\right) \\ & =2 a b c+2 c b^2-2 b c^2-2 b^2 c+2 b c^2+2 a b c \\ & =4 a b c \end{aligned} $$

Example 15 If $x, y, z$ are different and $\Delta=\left|\begin{array}{lll}x & x^2 & 1+x^3 \\ y & y^2 & 1+y^3 \\ z & z^2 & 1+z^3\end{array}\right|=0$, then show that $1+x y z=0$

Solution We have $$ \Delta=\left|\begin{array}{ccc} x & x^2 & 1+x^3 \\ y & y^2 & 1+y^3 \\ z & z^2 & 1+z^3 \end{array}\right| $$

$=\left|\begin{array}{ccc}x & x^2 & 1 \\ y & y^2 & 1 \\ z & z^2 & 1\end{array}\right|+\left|\begin{array}{ccc}x & x^2 & x^3 \\ y & y^2 & y^3 \\ z & z^2 & z^3\end{array}\right| \quad$ (Using Property 5)

$=(-1)^2\left|\begin{array}{lll}1 & x & x^2 \\ 1 & y & y^2 \\ 1 & z & z^2\end{array}\right|+x y z\left|\begin{array}{ccc}1 & x & x^2 \\ 1 & y & y^2 \\ 1 & z & z^2\end{array}\right|$ (Using $\mathrm{C}_3 \leftrightarrow \mathrm{C}_2$ and then $\mathrm{C}_1 \leftrightarrow \mathrm{C}_2$ ) $$ =\left|\begin{array}{lll} 1 & x & x^2 \\ 1 & y & y^2 \\ 1 & z & z^2 \end{array}\right|(1+x y z) $$

$$ =(1+x y z)\left|\begin{array}{ccc} 1 & x & x^2 \\ 0 & y-x & y^2-x^2 \\ 0 & z-x & z^2-x^2 \end{array}\right| $$ (Using $\mathrm{R}_2 \rightarrow \mathrm{R}_2-\mathrm{R}_1$ and $\mathrm{R}_3 \rightarrow \mathrm{R}_3-\mathrm{R}_1$ )

Taking out common factor $(y-x)$ from $\mathrm{R}_2$ and $(z-x)$ from $\mathrm{R}_3$, we get $$ \begin{aligned} \Delta & =(1+x y z)(y-x)(z-x)\left|\begin{array}{ccc} 1 & x & x^2 \\ 0 & 1 & y+x \\ 0 & 1 & z+x \end{array}\right| \\ & \left.=(1+x y z)(y-x)(z-x)(z-y) \text { (on expanding along } C_1\right) \end{aligned} $$

Since $\Delta=0$ and $x, y, z$ are all different, i.e., $x-y \neq 0, y-z \neq 0, z-x \neq 0$, we get $1+x y z=0$

Example 16 Show that $$ \left|\begin{array}{ccc} 1+a & 1 & 1 \\ 1 & 1+b & 1 \\ 1 & 1 & 1+c \end{array}\right|=a b c\left(1+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)=a b c+b c+c a+a b $$

Solution Taking out factors $a, b, c$ common from $\mathrm{R}_1, \mathrm{R}_2$ and $\mathrm{R}_3$, we get

$$ \text { L.H.S. }=a b c\left|\begin{array}{ccc} \frac{1}{a}+1 & \frac{1}{a} & \frac{1}{a} \\ \frac{1}{b} & \frac{1}{b}+1 & \frac{1}{b} \\ \frac{1}{c} & \frac{1}{c} & \frac{1}{c}+1 \end{array}\right| $$

Applying $R_1 \rightarrow R_1+R_2+R_3$, we have $$ \Delta=a b c\left|\begin{array}{ccc} 1+\frac{1}{a}+\frac{1}{b}+\frac{1}{c} & 1+\frac{1}{a}+\frac{1}{b}+\frac{1}{c} & 1+\frac{1}{a}+\frac{1}{b}+\frac{1}{c} \\ \frac{1}{b} & \frac{1}{b}+1 & \frac{1}{b} \\ \frac{1}{c} & \frac{1}{c} & \frac{1}{c}+1 \end{array}\right| $$

$$ =a b c\left(1+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\left|\begin{array}{ccc} 1 & 1 & 1 \\ \frac{1}{b} & \frac{1}{b}+1 & \frac{1}{b} \\ \frac{1}{c} & \frac{1}{c} & \frac{1}{c}+1 \end{array}\right| $$

Now applying $\mathrm{C}_2 \rightarrow \mathrm{C}_2-\mathrm{C}_1, \mathrm{C}_3 \rightarrow \mathrm{C}_3-\mathrm{C}_1$, we get $$ \begin{aligned} \Delta & =a b c\left(1+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\left|\begin{array}{ccc} 1 & 0 & 0 \\ \frac{1}{b} & 1 & 0 \\ \frac{1}{c} & 0 & 1 \end{array}\right| \\ & =a b c\left(1+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)[1(1-0)] \ & =a b c\left(1+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)=a b c+b c+c a+a b=\text { R.H.S. } \end{aligned} $$

Note Alternately try by applying $\mathrm{C}_1 \rightarrow \mathrm{C}_1-\mathrm{C}_2$ and $\mathrm{C}_3 \rightarrow \mathrm{C}_3-\mathrm{C}_2$, then apply $$ \mathrm{C}_1 \rightarrow \mathrm{C}_1-a \mathrm{C}_3 $$

EXERCISE 4.2

Using the property of determinants and without expanding in Exercises 1 to 7, prove that:

1. $\left|\begin{array}{lll}x & a & x+a \\ y & b & y+b \\ z & c & z+c\end{array}\right|=0$ $\quad\quad$

Solution

$ \begin{vmatrix} x & a & x+a \\ y & b & y+b \\ z & c & z+c \end{vmatrix} = \begin{vmatrix} x & a & x \\ y & b & y \\ z & c & z \end{vmatrix} + \begin{vmatrix} x & a & a \\ y & b & b \\ z & c & c \end{vmatrix} =0+0=0 $

[Here, the two columns of the determinants are identical]

2. $\left|\begin{array}{lll}a-b & b-c & c-a \\ b-c & c-a & a-b \\ c-a & a-b & b-c\end{array}\right|=0$

Solution

$ \Delta= \begin{vmatrix} a-b & b-c & c-a \\ b-c & c-a & a-b \\ c-a & a-b & b-c \end{vmatrix} $

Applying $R_1 \to R_1+R_2$, we have:

$ \begin{aligned} \Delta & = \begin{vmatrix} a-c & b-a & c-b \\ b-c & c-a & a-b \\ -(a-c) & -(b-a) & -(c-b) \end{vmatrix} \\ & =- \begin{vmatrix} a-c & b-a & c-b \\ b-c & c-a & a-b \\ a-c & b-a & c-b \end{vmatrix} \end{aligned} $

Here, the two rows $R_1$ and $R_3$ are identical.

$\therefore \Delta=0$.

3. $\left|\begin{array}{lll}2 & 7 & 65 \\ 3 & 8 & 75 \\ 5 & 9 & 86\end{array}\right|=0$ $\quad\quad\quad\quad$

Solution

$ \begin{vmatrix} 2 & 7 & 65 \\ 3 & 8 & 75 \\ 5 & 9 & 86\end{vmatrix} = \begin{vmatrix} 2 & 7 & 63+2 \\ 3 & 8 & 72+3 \\ 5 & 9 & 81+5\end{vmatrix} $

$= \begin{vmatrix} 2 & 7 & 63 \\ 3 & 8 & 72 \\ 5 & 9 & 81\end{vmatrix} + \begin{vmatrix} 2 & 7 & 2 \\ 3 & 8 & 3 \\ 5 & 9 & 5\end{vmatrix} $

$= \begin{vmatrix} 2 & 7 & 9(7) \\ 3 & 8 & 9(8)\end{vmatrix} +0 \quad$ [Two columns are identical]

$\begin{matrix} 5 & 9 & 9(9)\end{matrix} $

$=9 \begin{vmatrix} 2 & 7 & 7 \\ 3 & 8 & 8 \\ 5 & 9 & 9\end{vmatrix} $

$=0 \quad$ [Two columns are identical]

4. $\left|\begin{array}{lll}1 & b c & a(b+c) \\ 1 & c a & b(c+a) \\ 1 & a b & c(a+b)\end{array}\right|=0$

Solution

$\Delta= \begin{vmatrix} 1 & b c & a(b+c) \\ 1 & c a & b(c+a) \\ 1 & a b & c(a+b)\end{vmatrix} $

By applying $C_3 \to C_3+C_2$, we have:

$\Delta= \begin{vmatrix} 1 & b c & a b+b c+c a \\ 1 & c a & a b+b c+c a \\ 1 & a b & a b+b c+c a\end{vmatrix} $

Here, two columns $C_1$ and $C_3$ are proportional.

$\therefore \Delta=0$.

5. $\left|\begin{array}{ccc}b+c & q+r & y+z \\ c+a & r+p & z+x \\ a+b & p+q & x+y\end{array}\right|=2\left|\begin{array}{ccc}a & p & x \\ b & q & y \\ c & r & z\end{array}\right|$

Solution

$$ \begin{align*} \Delta & = \begin{vmatrix} b+c & q+r & y+z \\ c+a & r+p & z+x \\ a+b & p+q & x+y \end{vmatrix} \\ & = \begin{vmatrix} b+c & q+r & y+z \\ c+a & r+p & z+x \\ a & p & x \end{vmatrix} + \begin{vmatrix} b+c & q+r & y+z \\ c+a & r+p & z+x \\ b & q & y \end{vmatrix} \\ & =\Delta_1+\Delta_2 \text{ (say) } \tag{1} \end{align*} $$

Now, $\Delta_1= \begin{vmatrix} b+c & q+r & y+z \\ c+a & r+p & z+x \\ a & p & x\end{vmatrix} $

Applying $R_2 \to R_2-R_3$, we have:

$\Delta_1= \begin{vmatrix} b+c & q+r & y+z \\ c & r & z \\ a & p & x\end{vmatrix} $

Applying $R_1 \to R_1-R_2$, we have:

$\Delta_1= \begin{vmatrix} b & q & y \\ c & r & z \\ a & p & x\end{vmatrix} $

Applying $R_1 rightarrow R_3$ and $R_2 rightarrow R_3$, we have:

$\Delta_1=(-1)^{2} \begin{vmatrix} a & p & x \\ b & q & y \\ c & r & z\end{vmatrix} = \begin{vmatrix} a & p & x \\ b & q & y \\ c & r & z\end{vmatrix} $

$\Delta_2= \begin{vmatrix} b+c & q+r & y+z \\ c+a & r+p & z+x \\ b & q & y\end{vmatrix} $

Applying $R_1 \to R_1-R_3$, we have:

$\Delta_2= \begin{vmatrix} c & r & z \\ c+a & r+p & z+x \\ b & q & y\end{vmatrix} $

Applying $R_2 \to R_2-R_1$, we have:

$\Delta_2= \begin{vmatrix} c & r & z \\ a & p & x \\ b & q & y\end{vmatrix} $

Applying $R_1 rightarrow R_2$ and $R_2 rightarrow R_3$, we have:

$\Delta_2=(-1)^{2} \begin{vmatrix} a & p & x \\ b & q & y \\ c & r & z\end{vmatrix} = \begin{vmatrix} a & p & x \\ b & q & y \\ c & r & z\end{vmatrix} $

From (1), (2), and (3), we have:

$\Delta=2 \begin{vmatrix} a & p & x \\ b & q & y \\ c & r & z\end{vmatrix} $

Hence, the given result is proved.

6. $ \begin{vmatrix} 0 & a & -b \\ -a & 0 & -c \\ b & c & 0\end{vmatrix} =0$

Solution

We have,

$\Delta= \begin{vmatrix} 0 & a & -b \\ -a & 0 & -c \\ b & c & 0\end{vmatrix} $

Applying $R_1 \to c R_1$, we have:

$\Delta=\frac{1}{c} \begin{vmatrix} 0 & a c & -b c \\ -a & 0 & -c \\ b & c & 0\end{vmatrix} $

Applying $R_1 \to R_1-b R_2$, we have:

$\Delta=\frac{1}{c} \begin{vmatrix} a b & a c & 0 \\ -a & 0 & -c \\ b & c & 0\end{vmatrix} $

$=\frac{a}{c} \begin{vmatrix} b & c & 0 \\ -a & 0 & -c \\ b & c & 0\end{vmatrix} $

Here, the two rows $R_1$ and $R_3$ are identical.

$\therefore \Delta=0$.

7. $\left|\begin{array}{ccc}-a^2 & a b & a c \\ b a & -b^2 & b c \\ c a & c b & -c^2\end{array}\right|=4 a^2 b^2 c^2$

By using properties of determinants, in Exercises 8 to 14, show that:

(i) $\left|\begin{array}{lll}1 & a & a^2 \\ 1 & b & b^2 \\ 1 & c & c^2\end{array}\right|=(a-b)(b-c)(c-a)$

(ii) $\left|\begin{array}{lll}1 & 1 & 1 \\ a & b & c \\ a^3 & b^3 & c^3\end{array}\right|=(a-b)(b-c)(c-a)(a+b+c)$

Solution

$ \begin{aligned} & \Delta= \begin{vmatrix} -a^{2} & a b & a c \\ b a & -b^{2} & b c \\ c a & c b & -c^{2} \end{vmatrix} \\ & =a b c \begin{vmatrix} -a & b & c \\ a & -b & c \\ a & b & -c \end{vmatrix} \quad \text{ [Taking out factors } a, b, c \text{ from } R_1, R_2 \text{, and } R_3 \text{ ] } \\ & =a^{2} b^{2} c^{2} \begin{vmatrix} -1 & 1 & 1 \\ 1 & -1 & 1 \\ 1 & 1 & -1 \end{vmatrix} \quad \text{ [Taking out factors } a, b, c \text{ from } C_1, C_2 \text{, and } C_3 \text{ ] } \end{aligned} $

Applying $R_2 \to R_2+R_1$ and $R_3 \to R_3+R_1$, we have:

$ \begin{aligned} \Delta & =a^{2} b^{2} c^{2} \begin{vmatrix} -1 & 1 & 1 \\ 0 & 0 & 2 \\ 0 & 2 & 0 \end{vmatrix} \\ & =a^{2} b^{2} c^{2}(-1) \begin{vmatrix} 0 & 2 \\ 2 & 0 \end{vmatrix} \\ & =-a^{2} b^{2} c^{2}(0-4)=4 a^{2} b^{2} c^{2} \end{aligned} $

8. $\left|\begin{array}{lll}x & x^2 & y z \\ y & y^2 & z x \\ z & z^2 & x y\end{array}\right|=(x-y)(y-z)(z-x)(x y+y z+z x)$

Solution

Let $\Delta= \begin{vmatrix} x & x^{2} & y z \\ y & y^{2} & z x \\ z & z^{2} & x y\end{vmatrix} $.

Applying $R_2 \to R_2-R_1$ and $R_3 \to R_3-R_1$, we have:

$\Delta= \begin{vmatrix} x & x^{2} & y z \\ y-x & y^{2}-x^{2} & z x-y z \\ z-x & z^{2}-x^{2} & x y-y z\end{vmatrix} $

$= \begin{vmatrix} x & x^{2} & y z \\ -(x-y) & -(x-y)(x+y) & z(x-y) \\ (z-x) & (z-x)(z+x) & -y(z-x)\end{vmatrix} $

$=(x-y)(z-x) \begin{vmatrix} x & x^{2} & y z \\ -1 & -x-y & z \\ 1 & z+x & -y\end{vmatrix} $

Applying $R_3 \to R_3+R_2$, we have:

$ \begin{aligned} \Delta & =(x-y)(z-x) \begin{vmatrix} x & x^{2} & y z \\ -1 & -x-y & z \\ 0 & z-y & z-y \end{vmatrix} \\ & =(x-y)(z-x)(z-y) \begin{vmatrix} x & x^{2} & y z \\ -1 & -x-y & z \\ 0 & 1 & 1 \end{vmatrix} \end{aligned} $

Expanding along $R_3$, we have:

$$ \begin{aligned} \Delta & =[(x-y)(z-x)(z-y)][(-1)] \begin{vmatrix} x & y z \\ -1 & z \\ \end{vmatrix} +1 \begin{vmatrix} x & x^{2} \\ -1 & -x-y \\ \end{vmatrix} \\ & =(x-y)(z-x)(z-y)[(-x z-y z)+(-x^{2}-x y+x^{2})] \\ & =-(x-y)(z-x)(z-y)(x y+y z+z x) \\ & =(x-y)(y-z)(z-x)(x y+y z+z x) \end{aligned} $$

Hence, the given result is proved.

9. (i) $\left|\begin{array}{ccc}x+4 & 2 x & 2 x \\ 2 x & x+4 & 2 x \\ 2 x & 2 x & x+4\end{array}\right|=(5 x+4)(4-x)^2$

(ii) $\left|\begin{array}{ccc}y+k & y & y \\ y & y+k & y \\ y & y & y+k\end{array}\right|=k^2(3 y+k)$

Solution

(i) $\Delta= \begin{vmatrix} x+4 & 2 x & 2 x \\ 2 x & x+4 & 2 x \\ 2 x & 2 x & x+4\end{vmatrix} $

Applying $R_1 \to R_1+R_2+R_3$, we have:

$ \begin{aligned} & \Delta= \begin{vmatrix} 5 x+4 & 5 x+4 & 5 x+4 \\ 2 x & x+4 & 2 x \\ 2 x & 2 x & x+4 \end{vmatrix} \\ & =(5 x+4) \begin{vmatrix} 1 & 1 & 1 \\ 2 x & x+4 & 2 x \\ 2 x & 2 x & x+4 \end{vmatrix} \end{aligned} $

Applying $C_2 \to C_2-C_1, C_3 \to C_3-C_1$, we have:

$ \begin{aligned} \Delta & =(5 x+4) \begin{vmatrix} 1 & 0 & 0 \\ 2 x & -x+4 & 0 \\ 2 x & 0 & -x+4 \end{vmatrix} \\ & =(5 x+4)(4-x)(4-x) \begin{vmatrix} 1 & 0 & 0 \\ 2 x & 1 & 0 \\ 2 x & 0 & 1 \end{vmatrix} \end{aligned} $

Expanding along $C_3$, we have:

$ \begin{aligned} \Delta & =(5 x+4)(4-x)^{2} \begin{vmatrix} 1 & 0 \\ 2 x & 1 \end{vmatrix} \\ & =(5 x+4)(4-x)^{2} \end{aligned} $

Hence, the given result is proved.

(ii) $\Delta= \begin{vmatrix} y+k & y & y \\ y & y+k & y \\ y & y & y+k\end{vmatrix} $

Applying $R_1 \to R_1+R_2+R_3$, we have:

$ \begin{aligned} \Delta & = \begin{vmatrix} 3 y+k & 3 y+k & 3 y+k \\ y & y+k & y \\ y & y & y+k \end{vmatrix} \\ & =(3 y+k) \begin{vmatrix} 1 & 1 & 1 \\ y & y+k & y \\ y & y & y+k \end{vmatrix} \end{aligned} $

Applying $C_2 \to C_2-C_1$ and $C_3 \to C_3-C_1$, we have:

$ \begin{aligned} \Delta & =(3 y+k) \begin{vmatrix} 1 & 0 & 0 \\ y & k & 0 \\ y & 0 & k \end{vmatrix} \\ & =k^{2}(3 y+k) \begin{vmatrix} 1 & 0 & 0 \\ y & 1 & 0 \\ y & 0 & 1 \end{vmatrix} \end{aligned} $

Expanding along $C_3$, we have: $\Delta=k^{2}(3 y+k) \begin{vmatrix} 1 & 0 \\ y & 1\end{vmatrix} =k^{2}(3 y+k)$

Hence, the given result is proved.

10.(i) $\left|\begin{array}{ccc}a-b-c & 2 a & 2 a \\ 2 b & b-c-a & 2 b \\ 2 c & 2 c & c-a-b\end{array}\right|=(a+b+c)^3$

(ii) $\left|\begin{array}{ccc}x+y+2 z & x & y \\ z & y+z+2 x & y \\ z & x & z+x+2 y\end{array}\right|=2(x+y+z)^3$

Solution

(i) $\Delta= \begin{vmatrix} a-b-c & 2 a & 2 a \\ 2 b & b-c-a & 2 b \\ 2 c & 2 c & c-a-b\end{vmatrix} $

Applying $R_1 \to R_1+R_2+R_3$, we have:

$\begin{aligned} \Delta & = \begin{vmatrix} a+b+c & a+b+c & a+b+c \\ 2 b & b-c-a & 2 b \\ 2 c & 2 c & c-a-b\end{vmatrix} \\ & =(a+b+c) \begin{vmatrix} 1 & 1 & 1 \\ 2 b & b-c-a & 2 b \\ 2 c & 2 c & c-a-b\end{vmatrix} \end{aligned}$

Applying $C_2 \to C_2-C_1, C_3 \to C_3-C_1$, we have:

$\begin{aligned} \Delta & =(a+b+c) \begin{vmatrix} 1 & 0 & 0 \\ 2 b & -(a+b+c) & 0 \\ 2 c & 0 & -(a+b+c)\end{vmatrix} \\ & =(a+b+c)^{3} \begin{vmatrix} 1 & 0 & 0 \\ 2 b & -1 & 0 \\ 2 c & 0 & -1\end{vmatrix} \end{aligned}$

Expanding along $C_3$, we have:

$\Delta=(a+b+c)^{3}(-1)(-1)=(a+b+c)^{3}$

Hence, the given result is proved.

(ii) $\Delta= \begin{vmatrix} x+y+2 z & x & y \\ z & y+z+2 x & y \\ z & x & z+x+2 y\end{vmatrix} $

Applying $C_1 \to C_1+C_2+C_3$, we have:

$ \begin{aligned} \Delta & = \begin{vmatrix} 2(x+y+z) & x & y \\ 2(x+y+z) & y+z+2 x & y \\ 2(x+y+z) & x & z+x+2 y \end{vmatrix} \\ & =2(x+y+z) \begin{vmatrix} 1 & x & y \\ 1 & y+z+2 x & y \\ 1 & x & z+x+2 y \end{vmatrix} \end{aligned} $

Applying $R_2 \to R_2-R_1$ and $R_3 \to R_3-R_1$, we have:

$ \begin{aligned} & \Delta=2(x+y+z) \begin{vmatrix} 1 & x & y \\ 0 & x+y+z & 0 \\ 0 & 0 & x+y+z \end{vmatrix} \\ & =2(x+y+z)^{3} \begin{vmatrix} 1 & x & y \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{vmatrix} \end{aligned} $

Expanding along $R_3$, we have:

$\Delta=2(x+y+z)^{3}(1)(1-0)=2(x+y+z)^{3}$

Hence, the given result is proved.

11. $\left|\begin{array}{ccc}1 & x & x^2 \\ x^2 & 1 & x \\ x & x^2 & 1\end{array}\right|=\left(1-x^3\right)^2$

Solution

$\Delta= \begin{vmatrix} 1 & x & x^{2} \\ x^{2} & 1 & x \\ x & x^{2} & 1\end{vmatrix} $

Applying $R_1 \to R_1+R_2+R_3$, we have:

$ \begin{aligned} \Delta & = \begin{vmatrix} 1+x+x^{2} & 1+x+x^{2} & 1+x+x^{2} \\ x^{2} & 1 & x \\ x & x^{2} & 1 \end{vmatrix} \\ & =(1+x+x^{2}) \begin{vmatrix} 1 & 1 & 1 \\ x^{2} & 1 & x \\ x & x^{2} & 1 \end{vmatrix} \end{aligned} $

Applying $C_2 \to C_2-C_1$ and $C_3 \to C_3-C_1$, we have:

$ \begin{aligned} \Delta & =(1+x+x^{2}) \begin{vmatrix} 1 & 0 & 0 \\ x^{2} & 1-x^{2} & x-x^{2} \\ x & x^{2}-x & 1-x \end{vmatrix} \\ & =(1+x+x^{2})(1-x)(1-x) \begin{vmatrix} 1 & 0 & 0 \\ x^{2} & 1+x & x \\ x & -x & 1 \end{vmatrix} \\ & =(1-x^{3})(1-x) \begin{vmatrix} 1 & 0 & 0 \\ x^{2} & 1+x & x \\ x & -x & 1 \end{vmatrix} \end{aligned} $

Expanding along $R_1$, we have:

$ \begin{aligned} \Delta & =(1-x^{3})(1-x)(1) \begin{vmatrix} 1+x & x \\ -x & 1 \end{vmatrix} \\ & =(1-x^{3})(1-x)(1+x+x^{2}) \\ & =(1-x^{3})(1-x^{3}) \\ & =(1-x^{3})^{2} \end{aligned} $

Hence, the given result is proved.

12. $\left|\begin{array}{ccc}1+a^2-b^2 & 2 a b & -2 b \\ 2 a b & 1-a^2+b^2 & 2 a \\ 2 b & -2 a & 1-a^2-b^2\end{array}\right|=\left(1+a^2+b^2\right)^3$

Solution

$ \Delta= \begin{vmatrix} 1+a^{2}-b^{2} & 2 a b & -2 b \\ 2 a b & 1-a^{2}+b^{2} & 2 a \\ 2 b & -2 a & 1-a^{2}-b^{2} \end{vmatrix} $

Applying $R_1 \to R_1+b R_3$ and $R_2 \to R_2-a R_3$, we have:

$ \begin{aligned} \Delta & = \begin{vmatrix} 1+a^{2}+b^{2} & 0 & -b(1+a^{2}+b^{2}) \\ 0 & 1+a^{2}+b^{2} & a(1+a^{2}+b^{2}) \\ 2 b & -2 a & 1-a^{2}-b^{2} \end{vmatrix} \\ & =(1+a^{2}+b^{2})^{2} \begin{vmatrix} 1 & 0 & -b \\ 0 & 1 & a \\ 2 b & -2 a & 1-a^{2}-b^{2} \end{vmatrix} \end{aligned} $

Expanding along $R_1$, we have:

$ \begin{aligned} \Delta & =(1+a^{2}+b^{2})^{2}[(1) \begin{vmatrix} 1 & a \\ -2 a & 1-a^{2}-b^{2} \end{vmatrix} -b \begin{vmatrix} 0 & 1 \\ 2 b & -2 a \end{vmatrix} ] \\ & =(1+a^{2}+b^{2})^{2}[1-a^{2}-b^{2}+2 a^{2}-b(-2 b)] \\ & =(1+a^{2}+b^{2})^{2}(1+a^{2}+b^{2}) \\ & =(1+a^{2}+b^{2})^{3} \end{aligned} $

13. $\left|\begin{array}{ccc}a^2+1 & a b & a c \\ a b & b^2+1 & b c \\ c a & c b & c^2+1\end{array}\right|=1+a^2+b^2+c^2$

Solution

$ \Delta= \begin{vmatrix} a^{2}+1 & a b & a c \\ a b & b^{2}+1 & b c \\ c a & c b & c^{2}+1 \end{vmatrix} $

Taking out common factors $a, b$, and $c$ from $R_1, R_2$, and $R_3$ respectively, we have:

$ \Delta=a b c \begin{vmatrix} a+\frac{1}{a} & b & c \\ a & b+\frac{1}{b} & c \\ a & b & c+\frac{1}{c} \end{vmatrix} $

Applying $R_2 \to R_2-R_1$ and $R_3 \to R_3-R_1$, we have:

$\Delta=a b c \begin{vmatrix} a+\frac{1}{a} & b & c \\ -\frac{1}{a} & \frac{1}{b} & 0 \\ -\frac{1}{a} & 0 & \frac{1}{c}\end{vmatrix} $

Applying $C_1 \to a C_1, C_2 \to b C_2$, and $C_3 \to c C_3$, we have:

$ \begin{aligned} \Delta & =a b c \times \frac{1}{a b c} \lvert, \begin{matrix} a^{2}+1 & b \\ -1 & 1 \\ -1 & \end{matrix} . \\ & = \begin{vmatrix} a^{2}+1 & b^{2} & c^{2} \\ -1 & 1 & 0 \\ -1 & 0 & 1 \end{vmatrix} \end{aligned} $

Expanding along $R_3$, we have:

$ \begin{aligned} \Delta & =-1 \begin{vmatrix} b^{2} & c^{2} \\ 1 & 0 \end{vmatrix} +1 \begin{vmatrix} a^{2}+1 & b^{2} \\ -1 & 1 \end{vmatrix} \\ & =-1(-c^{2})+(a^{2}+1+b^{2})=1+a^{2}+b^{2}+c^{2} \end{aligned} $

Hence, the given result is proved.

Choose the correct answer in Exercises 15 and 16.

14. Let $\mathrm{A}$ be a square matrix of order $3 \times 3$, then $|k \mathrm{~A}|$ is equal to (A) $k|\mathrm{~A}|$ (B) $k^2|\mathrm{~A}|$ (C) $k^3|\mathrm{~A}|$ (D) $3 k|\mathrm{~A}|$

Solution

$A$ is a square matrix of order $3 \times 3$.

Let $A= \begin{vmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{vmatrix} $.

Then, $k A= \begin{vmatrix} k a_1 & k b_1 & k c_1 \\ k a_2 & k b_2 & k c_2 \\ k a_3 & k b_3 & k c_3 \end{vmatrix} $.

$\therefore|k A|= \begin{vmatrix} k a_1 & k b_1 & k c_1 \\ k a_2 & k b_2 & k c_2 \\ k a_3 & k b_3 & k c_3\end{vmatrix} $

$=k^{3} \begin{vmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3\end{vmatrix} $

$=k^{3}|A|$

$\therefore|k A|=k^{3}|A|$

Hence, the correct answer is C.

15. Which of the following is correct (A) Determinant is a square matrix. (B) Determinant is a number associated to a matrix. (C) Determinant is a number associated to a square matrix. (D) None of these

$f(n)=\frac{n 1}{2}$, if $n$ is odd $\frac{n}{2}$, if $n$ is even

Solution

We know that to every square matrix, $A=[a i j]$ of order $n$. We can associate a number

called the determinant of square matrix $A$, where $a i j=(i, j)^{\text{th }}$ element of $A$.

Thus, the determinant is a number associated to a square matrix.

Hence, the correct answer is $C$.

Area of a Triangle

In earlier classes, we have studied that the area of a triangle whose vertices are $(x_1, y_1),(x_2, y_2)$ and $(x_3, y_3)$, is given by the expression $\frac{1}{2}[x_1(y_2-y_3)+x_2(y_3-y_1)+.$ $.x_3(y_1-y_2)]$. Now this expression can be written in the form of a determinant as

$ \Delta=\frac{1}{2}\begin{vmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{vmatrix} $

Remarks

(i) Since area is a positive quantity, we always take the absolute value of the determinant in (1).

(ii) If area is given, use both positive and negative values of the determinant for calculation.

(iii) The area of the triangle formed by three collinear points is zero.

Example 6 Find the area of the triangle whose vertices are $(3,8),(-4,2)$ and $(5,1)$.

Solution The area of triangle is given by

$ \Delta=\frac{1}{2}\begin{vmatrix} 3 & 8 & 1 \\ -4 & 2 & 1 \\ 5 & 1 & 1 \end{vmatrix} $

$ \begin{aligned} & =\frac{1}{2}[3(2-1)-8(-4-5)+1(-4-10)] \\ & =\frac{1}{2}(3+72-14)=\frac{61}{2} \end{aligned} $

Example 7 Find the equation of the line joining $A(1,3)$ and $B(0,0)$ using determinants and find $k$ if $D(k, 0)$ is a point such that area of triangle ABD is 3sq units.

Solution Let $P(x, y)$ be any point on $AB$. Then, area of triangle ABP is zero (Why?). So

$ \frac{1}{2}\begin{vmatrix} 0 & 0 & 1 \\ 1 & 3 & 1 \\ x & y & 1 \end{vmatrix}=0 $

This gives

$ \frac{1}{2}(y-3 x)=0 \text{ or } y=3 x $

which is the equation of required line $AB$.

Also, since the area of the triangle ABD is 3 sq. units, we have

$ \frac{1}{2}\begin{vmatrix} 1 & 3 & 1 \\ 0 & 0 & 1 \\ k & 0 & 1 \end{vmatrix}= \pm 3 $

This gives, $\frac{-3 k}{2}= \pm 3$, i.e., $k=\mp 2$.

EXERCISE 4.2

1. Find area of the triangle with vertices at the point given in each of the following :

(i) $(1,0),(6,0),(4,3)$

(ii) $(2,7),(1,1),(10,8)$

(iii) $(-2,-3),(3,2),(-1,-8)$

Solution

2. Show that points

$A(a, b+c), B(b, c+a), C(c, a+b)$ are collinear.

Solution

3. Find values of $k$ if area of triangle is 4 sq. units and vertices are

(i) $(k, 0),(4,0),(0,2)$

(ii) $(-2,0),(0,4),(0, k)$

Solution

4. (i) Find equation of line joining $(1,2)$ and $(3,6)$ using determinants.

(ii) Find equation of line joining $(3,1)$ and $(9,3)$ using determinants.

Solution

5. If area of triangle is 35 sq units with vertices $(2,-6),(5,4)$ and $(k, 4)$. Then $k$ is (A) 12 (B) -2 (C) $-12,-2$ (D) $12,-2$

Solution

Minors and Cofactors

In this section, we will learn to write the expansion of a determinant in compact form using minors and cofactors.

Definition 1 Minor of an element $a _{i j}$ of a determinant is the determinant obtained by deleting its $i$ th row and $j$ th column in which element $a _{i j}$ lies. Minor of an element $a _{i j}$ is denoted by $M _{i j}$.

Remark Minor of an element of a determinant of order $n(n \geq 2)$ is a determinant of order $n-1$.

Example 8 Find the minor of element 6 in the determinant $\Delta=\begin{vmatrix}1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9\end{vmatrix}$

Solution Since 6 lies in the second row and third column, its minor $M _{23}$ is given by

$ M _{23}=\begin{vmatrix} 1 & 2 \\ 7 & 8 \end{vmatrix}=8-14=-6 \text{ (obtained by deleting } R_2 \text{ and } C_3 \text{ in } \Delta \text{ ). } $

Definition 2 Cofactor of an element $a _{i j}$, denoted by $A _{i j}$ is defined by

$ A _{i j}=(-1)^{i+j} M _{i j} \text{, where } M _{i j} \text{ is minor of } a _{i j} \text{. } $

Example 9 Find minors and cofactors of all the elements of the determinant $\begin{vmatrix}1 & -2 \\ 4 & 3\end{vmatrix}$

Solution Minor of the element $a _{i j}$ is $M _{i j}$

Here $a _{11}=1$. So $M _{11}=$ Minor of $a _{11}=3$

$M _{12}=$ Minor of the element $a _{12}=4$

$M _{21}=$ Minor of the element $a _{21}=-2$

$M _{22}=$ Minor of the element $a _{22}=1$

Now, cofactor of $a _{i j}$ is $A _{i j}$. So

$A _{11}=(-1)^{1+1} \quad M _{11}=(-1)^{2}(3)=3$

$A _{12}=(-1)^{1+2} \quad M _{12}=(-1)^{3}(4)=-4$

$A _{21}=(-1)^{2+1} \quad M _{21}=(-1)^{3}(-2)=2$

$A _{22}=(-1)^{2+2} \quad M _{22}=(-1)^{4}(1)=1$

Example 10 Find minors and cofactors of the elements $a _{11}, a _{21}$ in the determinant

$ \Delta=\begin{vmatrix} a _{11} & a _{12} & a _{13} \\ a _{21} & a _{22} & a _{23} \\ a _{31} & a _{32} & a _{33} \end{vmatrix} $

Solution By definition of minors and cofactors, we have

Minor of $a _{11}=M _{11}=\begin{vmatrix}a _{22} & a _{23} \\ a _{32} & a _{33}\end{vmatrix}=a _{22} a _{33}-a _{23} a _{32}$

Cofactor of $a _{11}=A _{11}=(-1)^{1+1} \quad M _{11}=a _{22} a _{33}-a _{23} a _{32}$

Minor of $a _{21}=M _{21}=\begin{vmatrix}a _{12} & a _{13} \\ a _{32} & a _{33}\end{vmatrix}=a _{12} a _{33}-a _{13} a _{32}$

Cofactor of $a _{21}=A _{21}=(-1)^{2+1} \quad M _{21}=(-1)(a _{12} a _{33}-a _{13} a _{32})=-a _{12} a _{33}+a _{13} a _{32}$

Remark Expanding the determinant $\Delta$, in Example 21 , along $R_1$, we have

$ \begin{aligned} \Delta & =(-1)^{1+1} a _{11}\begin{vmatrix} a _{22} & a _{23} \\ a _{32} & a _{33} \end{vmatrix}+(-1)^{1+2} a _{12}\begin{vmatrix} a _{21} & a _{23} \\ a _{31} & a _{33} \end{vmatrix}+(-1)^{1+3} a _{13}\begin{vmatrix} a _{21} & a _{22} \\ a _{31} & a _{32} \end{vmatrix} \\ & =a _{11} A _{11}+a _{12} A _{12}+a _{13} A _{13} \text{, where } A _{i j} \text{ is cofactor of } a _{i j} \\ & =\text{ sum of product of elements of } R_1 \text{ with their corresponding cofactors } \end{aligned} $

Similarly, $\Delta$ can be calculated by other five ways of expansion that is along $R_2, R_3$, $C_1, C_2$ and $C_3$.

Hence $\Delta$ = sum of the product of elements of any row (or column) with their corresponding cofactors.

Note If elements of a row (or column) are multiplied with cofactors of any other row (or column), then their sum is zero. For example,

$ \begin{aligned} \Delta & =a _{11} A _{21}+a _{12} A _{22}+a _{13} A _{23} \\ & =a _{11}(-1)^{1+1}\begin{vmatrix} a _{12} & a _{13} \\ a _{32} & a _{33} \end{vmatrix}+a _{12}(-1)^{1+2}\begin{vmatrix} a _{11} & a _{13} \\ a _{31} & a _{33} \end{vmatrix}+a _{13}(-1)^{1+3}\begin{vmatrix} a _{11} & a _{12} \\ a _{31} & a _{32} \end{vmatrix} \\ & =\begin{vmatrix} a _{11} & a _{12} & a _{13} \\ a _{11} & a _{12} & a _{13} \\ a _{31} & a _{32} & a _{33} \end{vmatrix}=0 \text{ since } R_1 \text{ and } R_2 \text{ are identical } \end{aligned} $

Similarly, we can try for other rows and columns.

Example 11 Find minors and cofactors of the elements of the determinant

$ \begin{vmatrix} 2 & -3 & 5 \\ 6 & 0 & 4 \\ 1 & 5 & -7 \end{vmatrix} \text{ and verify that } a _{11} A _{31}+a _{12} A _{32}+a _{13} A _{33}=0 $

Solution We have $M _{11}=\begin{vmatrix}0 & 4 \\ 5 & -7\end{vmatrix}=0-20=-20 ; A _{11}=(-1)^{1+1}(-20)=-20$

$M _{12}=\begin{vmatrix}6 & 4 \\ 1 & -7\end{vmatrix}=-42-4=-46 ; \quad A _{12}=(-1)^{1+2}(-46)=46$

$M _{13}=\begin{vmatrix}6 & 0 \\ 1 & 5\end{vmatrix}=30-0=30 ; \quad A _{13}=(-1)^{1+3}(30)=30$

$M _{21}=\begin{vmatrix}-3 & 5 \\ 5 & -7\end{vmatrix}=21-25=-4 ; \quad A _{21}=(-1)^{2+1}(-4)=4$

$M _{22}=\begin{vmatrix}2 & 5 \\ 1 & -7\end{vmatrix}=-14-5=-19 ; \quad A _{22}=(-1)^{2+2}(-19)=-19$

$M _{23}=\begin{vmatrix}2 & -3 \\ 1 & 5\end{vmatrix}=10+3=13 ; \quad A _{23}=(-1)^{2+3}(13)=-13$

$M _{31}=\begin{vmatrix}-3 & 5 \\ 0 & 4\end{vmatrix}=-12-0=-12 ; \quad A _{31}=(-1)^{3+1}(-12)=-12$

$M _{32}=\begin{vmatrix}2 & 5 \\ 6 & 4\end{vmatrix}=8-30=-22 ; \quad A _{32}=(-1)^{3+2}(-22)=22$

and $\quad M _{33}=\begin{vmatrix}2 & -3 \\ 6 & 0\end{vmatrix}=0+18=18 ; \quad A _{33}=(-1)^{3+3}(18)=18$

Now $\quad a _{11}=2, a _{12}=-3, a _{13}=5 ; A _{31}=-12, A _{32}=22, A _{33}=18$

So $\quad a _{11} A _{31}+a _{12} A _{32}+a _{13} A _{33}$

$=2(-12)+(-3)(22)+5(18)=-24-66+90=0$

EXERCISE 4.3

Write Minors and Cofactors of the elements of following determinants:

1. (i) $\begin{vmatrix}2 & -4 \\ 0 & 3\end{vmatrix}$ $\quad\quad\quad$(ii) $\begin{vmatrix}a & c \\ b & d\end{vmatrix}$

Solution

(i) The given determinants is $\begin{vmatrix}2 & -4 \\ 0 & 3\end{vmatrix}$

Minor of element $a_{ij}$ is $M_{ij}$

$\therefore M _{11}=$ minor of element $a _{11}=3$

$M _{12}=$ minor of element $a _{12}=0$

$M _{21}=$ minor of element $a _{21}=-4$

$M _{22}=$ minor of element $a _{22}=2$

Cofactor of $a _{i j}$ is $A _{i j}=(-1)^{i+j} M _{i j}$.

$\therefore A _{11}=(-1)^{1+1} M _{11}=(-1)^{2}(3)=3$

$A _{12}=(-1)^{1+2} M _{12}=(-1)^{3}(0)=0$

$A _{21}=(-1)^{2+1} M _{21}=(-1)^{3}(-4)=4$

$A _{22}=(-1)^{2+2} M _{22}=(-1)^{4}(2)=2$

(ii) The given determinant is $ \begin{vmatrix} a & c \\ b & d\end{vmatrix} $. Minor of element $a _{i j}$ is $M _{i j}$. $\therefore M _{11}=$ minor of element $a _{11}=d$

$M _{12}=$ minor of element $a _{12}=b$

$M _{21}=$ minor of element $a _{21}=c$

$M _{22}=$ minor of element $a _{22}=a$

Cofactor of $a _{i j}$ is $A _{i j}=(-1)^{i+j} M _{i j}$.

$ \therefore A _{11}=(-1)^{1+1} M _{11}=(-1)^{2}(d)=d $

$A _{12}=(-1)^{1+2} M _{12}=(-1)^{3}(b)=-b$

$A _{21}=(-1)^{2+1} M _{21}=(-1)^{3}(c)=-c$

$A _{22}=(-1)^{2+2} M _{22}=(-1)^{4}(a)=a$

2. (i) $\begin{vmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{vmatrix}$ $\quad\quad\quad$(ii) $\begin{vmatrix}1 & 0 & 4 \\ 3 & 5 & -1 \\ 0 & 1 & 2\end{vmatrix}$

Solution

(i) The given determinant is $ \begin{vmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{vmatrix} $.

By the definition of minors and cofactors, we have:

$M _{11}=$ minor of $a _{11}= \begin{vmatrix} 1 & 0 \\ 0 & 1\end{vmatrix} =1$

$M _{12}=$ minor of $a _{12}= \begin{vmatrix} 0 & 0 \\ 0 & 1\end{vmatrix} =0$

$ \begin{aligned} & M _{13}=\text{ minor of } a _{13}= \begin{vmatrix} 0 & 1 \\ 0 & 0 \end{vmatrix} =0 \\ & M _{21}=\text{ minor of } a _{21}= \begin{vmatrix} 0 & 0 \\ 0 & 1 \end{vmatrix} =0 \\ & M _{22}=\text{ minor of } a _{22}= \begin{vmatrix} 1 & 0 \\ 0 & 1 \end{vmatrix} =1 \\ & M _{23}=\text{ minor of } a _{23}= \begin{vmatrix} 1 & 0 \\ 0 & 0 \end{vmatrix} =0 \\ & M _{31}=\text{ minor of } a _{31}= \begin{vmatrix} 0 & 0 \\ 1 & 0 \end{vmatrix} =0 \\ & M _{32}=\text{ minor of } a _{32}= \begin{vmatrix} 1 & 0 \\ 0 & 0 \end{vmatrix} =0 \\ & M _{33}=\text{ minor of } a _{33}= \begin{vmatrix} 1 & 0 \\ 0 & 1 \end{vmatrix} =1 \\ & A _{11}=\text{ cofactor of } a _{11}=(-1)^{1+1} M _{11}=1 \\ & A _{12}=\text{ cofactor of } a _{12}=(-1)^{1+2} M _{12}=0 \\ & A _{13}=\text{ cofactor of } a _{13}=(-1)^{1+3} M _{13}=0 \\ & A _{21}=\text{ cofactor of } a _{21}=(-1)^{2+1} M _{21}=0 \\ & A _{22}=\text{ cofactor of } a _{22}=(-1)^{2+2} M _{22}=1 \\ & A _{23}=\text{ cofactor of } a _{23}=(-1)^{2+3} M _{23}=0 \\ & A _{31}=\text{ cofactor of } a _{31}=(-1)^{3+1} M _{31}=0 \\ & A _{32}=\text{ cofactor of } a _{32}=(-1)^{3+2} M _{32}=0 \\ & A _{33}=\text{ cofactor of } a _{33}=(-1)^{3+3} M _{33}=1 \\ & \text{ (ii) The given determinant is } \begin{vmatrix} 1 & 0 & 4 \\ 3 & 5 & -1 \\ 0 & 1 & 2 \end{vmatrix} \text{. } \end{aligned} $

By definition of minors and cofactors, we have:

$ M _{11}=\text{ minor of } a _{11}= \begin{vmatrix} 5 & -1 \\ 1 & 2 \end{vmatrix} =10+1=11 $

$ \begin{aligned} & M _{12}=\text{ minor of } a _{12}= \begin{vmatrix} 3 & -1 \\ 0 & 2 \end{vmatrix} =6-0=6 \\ & M _{13}=\text{ minor of } a _{13}= \begin{vmatrix} 3 & 5 \\ 0 & 1 \end{vmatrix} =3-0=3 \\ & M _{21}=\text{ minor of } a _{21}= \begin{vmatrix} 0 & 4 \\ 1 & 2 \end{vmatrix} =0-4=-4 \\ & M _{22}=\text{ minor of } a _{22}= \begin{vmatrix} 1 & 4 \\ 0 & 2 \end{vmatrix} =2-0=2 \\ & M _{23}=\text{ minor of } a _{23}= \begin{vmatrix} 1 & 0 \\ 0 & 1 \end{vmatrix} =1-0=1 \\ & M _{31}=\text{ minor of } a _{31}= \begin{vmatrix} 0 & 4 \\ 5 & -1 \end{vmatrix} =0-20=-20 \\ & M _{32}=\text{ minor of } a _{32}= \begin{vmatrix} 1 & 4 \\ 3 & -1 \end{vmatrix} =-1-12=-13 \\ & A _{33}= \begin{vmatrix} 1 & 0 \\ 3 & 5 \end{vmatrix} =5-0=5 \\ & A _{32}=\text{ cofactor of } a _{32}=(-1)^{3+2} M _{32}=13 \\ & A _{11}=\text{ cofactor of } a _{33}=(-1)^{3+3} M _{33}=5 \\ & A _{12}=\text{ cofactor of } a _{12}=(-1)^{1+2} M _{12}=-6 \\ & A _{13}=\text{ cofactor of } a _{13}=(-1)^{1+3} M _{13}=3 \\ & A _{21}=\text{ cofactor of } a _{21}=(-1)^{2+1} M _{21}=4 \\ & A _{22}=\text{ cofactor of } a _{22}=(-1)^{2+2} M _{22}=2 \\ & A _{23}=\text{ cofactor of } a _{23}=(-1)^{2+3} M _{23}=-1 \\ & M _{11}=11 \end{aligned} $

3. Using Cofactors of elements of second row, evaluate $\Delta=\begin{vmatrix}5 & 3 & 8 \\ 2 & 0 & 1 \\ 1 & 2 & 3\end{vmatrix}$.

Solution

We have:

$M _{21}= \begin{vmatrix} 3 & 8 \\ 2 & 3\end{vmatrix} =9-16=-7$

$\therefore A _{21}=$ cofactor of $a _{21}=(-1)^{2+1} M _{21}=7$

$M _{22}= \begin{vmatrix} 5 & 8 \\ 1 & 3\end{vmatrix} =15-8=7$

$\therefore A _{22}=$ cofactor of $a _{22}=(-1)^{2+2} M _{22}=7$

$M _{23}= \begin{vmatrix} 5 & 3 \\ 1 & 2\end{vmatrix} =10-3=7$

$\therefore A _{23}=$ cofactor of $a _{23}=(-1)^{2+3} M _{23}=-7$

We know that $\Delta$ is equal to the sum of the product of the elements of the second row with their corresponding cofactors. $\therefore \Delta=a _{21} A _{21}+a _{22} A _{22}+a _{23} A _{23}=2(7)+0(7)+1(-7)=14-7=7$

4. Using Cofactors of elements of third column, evaluate $\Delta=\begin{vmatrix}1 & x & y z \\ 1 & y & z x \\ 1 & z & x y\end{vmatrix}$.

Solution

The given determinant is $ \begin{vmatrix} 1 & x & y z \\ 1 & y & z x \\ 1 & z & x y\end{vmatrix} $.

We have:

$ \begin{aligned} & M _{13}= \begin{vmatrix} 1 & y \\ 1 & z \end{vmatrix} =z-y \\ & M _{23}= \begin{vmatrix} 1 & x \\ 1 & z \end{vmatrix} =z-x \\ & M _{33}= \begin{vmatrix} 1 & x \\ 1 & y \end{vmatrix} =y-x \\ & \therefore A _{13}=\text{ cofactor of } a _{13}=(-1)^{1+3} M _{13}=(z-y) \end{aligned} $

$A _{23}=$ cofactor of $a _{23}=(-1)^{2+3} M _{23}=-(z-x)=(x-z)$

$A _{33}=$ cofactor of $a _{33}=(-1)^{3+3} M _{33}=(y-x)$

We know that $\Delta$ is equal to the sum of the product of the elements of the second row with their corresponding cofactors.

$ \begin{aligned} \therefore \Delta & =a _{13} A _{13}+a _{23} A _{23}+a _{33} A _{33} \\ & =y z(z-y)+z x(x-z)+x y(y-x) \\ & =y z^{2}-y^{2} z+x^{2} z-x z^{2}+x y^{2}-x^{2} y \\ & =(x^{2} z-y^{2} z)+(y z^{2}-x z^{2})+(x y^{2}-x^{2} y) \\ & =z(x^{2}-y^{2})+z^{2}(y-x)+x y(y-x) \\ & =z(x-y)(x+y)+z^{2}(y-x)+x y(y-x) \\ & =(x-y)[z x+z y-z^{2}-x y] \\ & =(x-y)[z(x-z)+y(z-x)] \\ & =(x-y)(z-x)[-z+y] \\ & =(x-y)(y-z)(z-x) \end{aligned} $

Hence, $\Delta=(x-y)(y-z)(z-x)$.

5. If $\Delta=\begin{vmatrix}a _{11} & a _{12} & a _{13} \\ a _{21} & a _{22} & a _{23} \\ a _{31} & a _{32} & a _{33}\end{vmatrix}$ and $A _{i j}$ is Cofactors of $a _{i j}$, then value of $\Delta$ is given by

(A) $a _{11} A _{31}+a _{12} A _{32}+a _{13} A _{33}$

(B) $a _{11} A _{11}+a _{12} A _{21}+a _{13} A _{31}$

(C) $a _{21} A _{11}+a _{22} A _{12}+a _{23} A _{13}$

(D) $a _{11} A _{11}+a _{21} A _{21}+a _{31} A _{31}$

Solution

Given,

$\begin{aligned} & \Delta=\left|\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right| \\ & =a_{11}\left|\begin{array}{ll} a_{22} & a_{23} \\ a_{32} & a_{33} \end{array}\right|-a_{12}\left|\begin{array}{ll} a_{21} & a_{23} \\ a_{31} & a_{33} \end{array}\right|+a_{13}\left|\begin{array}{ll} a_{21} & a_{22} \\ a_{31} & a_{32} \end{array}\right| \\ & =a_{11}(-1)^{1+1}\left|\begin{array}{ll} a_{22} & a_{23} \\ a_{32} & a_{33} \end{array}\right|+a_{12}(-1)^{1+2}\left|\begin{array}{ll} a_{21} & a_{23} \\ a_{31} & a_{33} \end{array}\right|+a_{13}(-1)^{1+3} & \left|\begin{array}{ll} a_{21} & a_{22} \\ a_{31} & a_{32} \end{array}\right| \\ & =a_{11} A_{11}+a_{21} A_{21}+a_{31} A_{31} \end{aligned}$

So, the correct option is D.

Adjoint and Inverse of a Matrix

In the previous chapter, we have studied inverse of a matrix. In this section, we shall discuss the condition for existence of inverse of a matrix.

To find inverse of a matrix A, i.e., $A^{-1}$ we shall first define adjoint of a matrix.

Adjoint of a matrix

Definition 3 The adjoint of a square matrix $A=[a _{i j}] _{n \times n}$ is defined as the transpose of the matrix $[A _{i j}] _{n \times n}$, where $A _{i j}$ is the cofactor of the element $a _{i j}$. Adjoint of the matrix A is denoted by adj $A$.

Let

$ A=\begin{vmatrix} a _{11} & a _{12} & a _{13} \\ a _{21} & a _{22} & a _{23} \\ a _{31} & a _{32} & a _{33} \end{vmatrix} $

Then $\quad adj A=$ Transpose of $\begin{vmatrix}A _{11} & A _{12} & A _{13} \\ A _{21} & A _{22} & A _{23} \\ A _{31} & A _{32} & A _{33}\end{vmatrix}=\begin{vmatrix}A _{11} & A _{21} & A _{31} \\ A _{12} & A _{22} & A _{32} \\ A _{13} & A _{23} & A _{33}\end{vmatrix}$

Example 12 Find $adj A$ for $A=\begin{vmatrix}2 & 3 \\ 1 & 4\end{vmatrix}$

Solution We have $A _{11}=4, A _{12}=-1, A _{21}=-3, A _{22}=2$

Hence

$ adj A=\begin{vmatrix} A _{11} & A _{21} \\ A _{12} & A _{22} \end{vmatrix}=\begin{vmatrix} 4 & -3 \\ -1 & 2 \end{vmatrix} $

Remark For a square matrix of order 2, given by

$ A=\begin{vmatrix} a _{11} & a _{12} \\ a _{21} & a _{22} \end{vmatrix} $

The $a d j$ A can also be obtained by interchanging $a _{11}$ and $a _{22}$ and by changing signs of $a _{12}$ and $a _{21}$, i.e.,

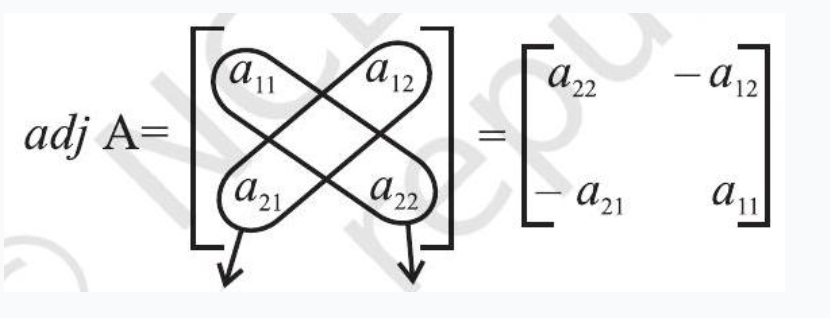
Change sign Interchange

We state the following theorem without proof.

Theorem 1 If $A$ be any given square matrix of order $n$, then

$ A(adj A)=(adj A) A=|A| I, $

where I is the identity matrix of order $n$

Verification

Let $\quad A=\begin{vmatrix}a _{11} & a _{12} & a _{13} \\ a _{21} & a _{22} & a _{23} \\ a _{31} & a _{32} & a _{33}\end{vmatrix}$, then $adj A=\begin{vmatrix}A _{11} & A _{21} & A _{31} \\ A _{12} & A _{22} & A _{32} \\ A _{13} & A _{23} & A _{33}\end{vmatrix}$

Since sum of product of elements of a row (or a column) with corresponding cofactors is equal to $|A|$ and otherwise zero, we have

$ A(adj A)=\begin{vmatrix} |A| & 0 & 0 \\ 0 & |A| & 0 \\ 0 & 0 & |A| \end{vmatrix}=|A\begin{vmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{vmatrix}=|A| I $

Similarly, we can show $(adj A) A=|A| I$

Hence $A(adj A)=(adj A) A=|A| I$

Definition 4 A square matrix $A$ is said to be singular if $|A|=0$.

For example, the determinant of matrix $A=\begin{vmatrix}1 & 2 \\ 4 & 8\end{vmatrix}$ is zero

Hence $A$ is a singular matrix.

Definition 5 A square matrix $A$ is said to be non-singular if $|A| \neq 0$

Let

$ A=\begin{vmatrix} 1 & 2 \\ 3 & 4 \end{vmatrix} . \text{ Then }|A|=\begin{vmatrix} 1 & 2 \\ 3 & 4 \end{vmatrix}=4-6=-2 \neq 0 $

Hence $A$ is a nonsingular matrix

We state the following theorems without proof.

Theorem 2 If $A$ and $B$ are nonsingular matrices of the same order, then $AB$ and $BA$ are also nonsingular matrices of the same order.

Theorem 3 The determinant of the product of matrices is equal to product of their respective determinants, that is, $|AB|=|A||B|$, where $A$ and $B$ are square matrices of the same order

Remark We know that (adj A) A= $ \begin{vmatrix} |A| & 0 & 0\\ 0 & |A| & 0\\ 0 & 0 & |A| \end{vmatrix} $

Writing determinants of matrices on both sides, we have

$ |(adj A) A|=\begin{vmatrix} |A| & 0 & 0 \\ 0 & |A| & 0 \\ 0 & 0 & |A| \end{vmatrix} $ i.e.

$ |(adj A)||A|=|A|^{3}\begin{vmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{vmatrix} $ i.e.

$ |(adj A)||A|=|A|^{3}(1) $ i.e.

$ |(adj A)|=|A|^{2} $

In general, if $A$ is $a$ square matrix of order $n$, then $|adj(A)|=|A|^{n-1}$.

Theorem 4 A square matrix $A$ is invertible if and only if $A$ is nonsingular matrix.

Proof Let A be invertible matrix of order $n$ and I be the identity matrix of order $n$.

Then, there exists a square matrix $B$ of order $n$ such that $AB=BA=I$

Now

$ AB=I \text{. So }|AB|=|I| \text{ or }|A||B|=1 \quad \text{ (since }|I|=1,|AB|=|A||B| \text{ ) } $

This gives $\quad|A| \neq 0$. Hence $A$ is nonsingular.

Conversely, let A be nonsingular. Then $|A| \neq 0$

Now

$ A(adj A)=(adj A) A=|A| I $

(Theorem 1)

or

$ A(\frac{1}{|A|} adj A)=(\frac{1}{|A|} adj A) A=I $

or

$ AB=BA=I \text{, where } B=\frac{1}{|A|} adj A $

Thus

$A$ is invertible and $A^{-1}=\frac{1}{|A|}$ adj $A$

$ 133 $

Example 13 If $A=\begin{matrix}1 & 3 & 3 \\ 1 & 4 & 3 \\ 1 & 3 & 4 \end{matrix}$, then verify that $A adj A=|A| I$. Also find $A^{-1}$.

4

Solution We have $|A|=1(16-9)-3(4-3)+3(3-4)=1 \neq 0$

Now $A _{11}=7, A _{12}=-1, A _{13}=-1, A _{21}=-3, A _{22}=1, A _{23}=0, A _{31}=-3, A _{32}=0$, $A _{33}=1$

Therefore

$ adj A=\begin{vmatrix} 7 & -3 & -3 \\ -1 & 1 & 0 \\ -1 & 0 & 1 \end{vmatrix} $

Now

$ \begin{aligned} A(adj A) & =\begin{vmatrix} 1 & 3 & 3 \\ 1 & 4 & 3 \\ 1 & 3 & 4 \end{vmatrix}\begin{vmatrix} 7 & -3 & -3 \\ -1 & 1 & 0 \\ -1 & 0 & 1 \end{vmatrix} \\ & =\begin{vmatrix} 7-3-3 & -3+3+0 & -3+0+3 \\ 7-4-3 & -3+4+0 & -3+0+3 \\ 7-3-4 & -3+3+0 & -3+0+4 \end{vmatrix} \\ & =\begin{vmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{vmatrix}=(1)\begin{vmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{vmatrix}=|A| . I \\ A^{-1}=\frac{1}{|A|} \text{ adj } A & =\frac{1}{1}\begin{vmatrix} 7 & -3 & -3 \\ -1 & 1 & 0 \\ -1 & 0 & 1 \end{vmatrix}=\begin{vmatrix} 7 & -3 & -3 \\ -1 & 1 & 0 \\ -1 & 0 & 1 \end{vmatrix} \end{aligned} $

Example 14 If $A=\begin{vmatrix}2 & 3 \\ 1 & -4\end{vmatrix}$ and $B=\begin{vmatrix}1 & -2 \\ -1 & 3\end{vmatrix}$, then verify that $(AB)^{-1}=B^{-1} A^{-1}$.

Solution We have $A B=\begin{vmatrix}2 & 3 \\ 1 & -4\end{vmatrix}\begin{vmatrix}1 & -2 \\ -1 & 3\end{vmatrix}=\begin{vmatrix}-1 & 5 \\ 5 & -14\end{vmatrix}$

Since, $|AB|=-11 \neq 0,(AB)^{-1}$ exists and is given by

$ (AB)^{-1}=\frac{1}{|AB|} adj(AB)=-\frac{1}{11}\begin{vmatrix} -14 & -5 \\ -5 & -1 \end{vmatrix}=\frac{1}{11}\begin{vmatrix} 14 & 5 \\ 5 & 1 \end{vmatrix} $

Further, $|A|=-11 \neq 0$ and $|B|=1 \neq 0$. Therefore, $A^{-1}$ and $B^{-1}$ both exist and are given by

$ A^{-1}=-\frac{1}{11} \begin{vmatrix} -4 & -3 \\ -1 & 2 \end{vmatrix}, B^{-1}=\begin{vmatrix} 3 & 2 \\ 1 & 1 \end{vmatrix} $

Therefore

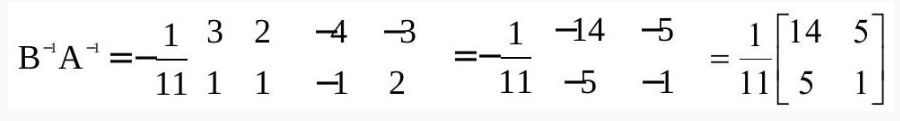
Hence $(AB)^{-1}=B^{-1} A^{-1}$

Example 15 Show that the matrix $A=\begin{vmatrix}2 & 3 \\ 1 & 2\end{vmatrix}$ satisfies the equation $A^{2}-4 A+I=O$, where $I$ is $2 \times 2$ identity matrix and $O$ is $2 \times 2$ zero matrix. Using this equation, find $A^{-1}$.

Solution We have $A^{2}=A . A=\begin{vmatrix}2 & 3 \\ 1 & 2\end{vmatrix}\begin{vmatrix}2 & 3 \\ 1 & 2\end{vmatrix}=\begin{vmatrix}7 & 12 \\ 4 & 7\end{vmatrix}$

Hence

$ A^{2}-4 A+I=\begin{vmatrix} 7 & 12 \\ 4 & 7 \end{vmatrix}-\begin{vmatrix} 8 & 12 \\ 4 & 8 \end{vmatrix}+\begin{vmatrix} 1 & 0 \\ 0 & 1 \end{vmatrix}=\begin{vmatrix} 0 & 0 \\ 0 & 0 \end{vmatrix}=O $

Now $\quad A^{2}-4 A+I=O$

Therefore

$ A A-4 A=-I $

or

A $A(A^{-1})-4 AA^{-1}=-IA^{-1}$ (Post multiplying by $A^{-1}$ because $|A| \neq 0$ )

or

$A(A A^{-1})-4 I=-A^{-1}$

or

$AI-4 I=-A^{-1}$

or

$A^{-1}=4 I-A=\begin{vmatrix}4 & 0 \\ 0 & 4\end{vmatrix}-\begin{vmatrix}2 & 3 \\ 1 & 2\end{vmatrix}=\begin{vmatrix}2 & -3 \\ -1 & 2\end{vmatrix}$

Hence

$ A^{-1}=\begin{vmatrix} 2 & -3 \\ -1 & 2 \end{vmatrix} $

EXERCISE 4.4

Find adjoint of each of the matrices in Exercises 1 and 2.

1. $\begin{vmatrix}1 & 2 \\ 3 & 4\end{vmatrix}$ $\quad\quad\quad$

Solution

Let $A= \begin{vmatrix} 1 & 2 \\ 3 & 4 \end{vmatrix} $.

We have,

$A _{11}=4, A _{12}=-3, A _{21}=-2, A _{22}=1$

$\therefore adj A= \begin{vmatrix} A _{11} & A _{21} \\ A _{12} & A _{22}\end{vmatrix} = \begin{vmatrix} 4 & -2 \\ -3 & 1 \end{vmatrix} $

2. $\begin{vmatrix}1 & -1 & 2 \\ 2 & 3 & 5\\ -2 & 0 & 1 \end{vmatrix}$ Verify $A(adj A)=(adj A) A=|A| I$ in Exercises 3 and 4

Solution

Let $A= \begin{cases} 1 & -1 & 2 \\ 2 & 3 & 5 \\ -2 & 0 & 1 \end{cases} $.

We have,

$A _{11}= \begin{vmatrix} 3 & 5 \\ 0 & 1\end{vmatrix} =3-0=3$

$A _{12}=- \begin{vmatrix} 2 & 5 \\ -2 & 1\end{vmatrix} =-(2+10)=-12$

$A _{13}= \begin{vmatrix} 2 & 3 \\ -2 & 0\end{vmatrix} =0+6=6$ $A _{21}=- \begin{vmatrix} -1 & 2 \\ 0 & 1\end{vmatrix} =-(-1-0)=1$

$A _{22}= \begin{vmatrix} 1 & 2 \\ -2 & 1\end{vmatrix} =1+4=5$

$A _{23}=- \begin{vmatrix} 1 & -1 \\ -2 & 0\end{vmatrix} =-(0-2)=2$

$A _{31}= \begin{vmatrix} -1 & 2 \\ 3 & 5\end{vmatrix} =-5-6=-11$

$A _{32}=- \begin{vmatrix} 1 & 2 \\ 2 & 5\end{vmatrix} =-(5-4)=-1$

$A _{33}= \begin{vmatrix} 1 & -1 \\ 2 & 3\end{vmatrix} =3+2=5$

Hence, adj $A= \begin{vmatrix} A _{11} & A _{21} & A _{31} \\ A _{12} & A _{22} & A _{32} \\ A _{13} & A _{23} & A _{33}\end{vmatrix} = \begin{vmatrix} 3 & 1 & -11 \\ -12 & 5 & -1 \\ 6 & 2 & 5 \end{vmatrix} $.

3. $\begin{vmatrix} 2 & 3 \\ -4 & -6 \end{vmatrix} $

Solution

$A= \begin{vmatrix} 2 & 3 \\ -4 & -6 \end{vmatrix} $

we have,

$|A|=-12-(-12)=-12+12=0$

$\therefore|A| I=0 \begin{vmatrix} 1 & 0 \\ 0 & 1\end{vmatrix} = \begin{vmatrix} 0 & 0 \\ 0 & 0 \end{vmatrix} $

Now,

$A _{11}=-6, A _{12}=4, A _{21}=-3, A _{22}=2$

$\therefore adj A= \begin{vmatrix} -6 & -3 \\ 4 & 2 \end{vmatrix} $

Now,

$ \begin{aligned} A(adj A) & = \begin{bmatrix} 2 & 3 \\ -4 & -6 \end{bmatrix} \begin{bmatrix} -6 & -3 \\ 4 & 2 \end{bmatrix} \\ & = \begin{bmatrix} -12+12 & -6+6 \\ 24-24 & 12-12 \end{bmatrix} = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} \end{aligned} $

Also, $(adj A) A= \begin{vmatrix} -6 & -3 \\ 4 & 2\end{vmatrix} \begin{vmatrix} 2 & 3 \\ -4 & -6 \end{vmatrix} $

$ = \begin{bmatrix} -12+12 & -18+18 \\ 8-8 & 12-12 \end{bmatrix} = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} $

Hence, $A(adj A)=(adj A) A=|A| I$.

4. $ \begin{vmatrix} 1 & -1 & 2\\ 3 & 0 & -2 \\ 1& 0 & 3 \end{vmatrix} $

Solution

$ \begin{aligned} & A= \begin{bmatrix} 1 & -1 & 2 \\ 3 & 0 & -2 \\ 1 & 0 & 3 \end{bmatrix} \\ & |A|=1(0-0)+1(9+2)+2(0-0)=11 \\ & \therefore|A| I=11 \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 11 & 0 & 0 \\ 0 & 11 & 0 \\ 0 & 0 & 11 \end{bmatrix} \end{aligned} $

Now,

$ \begin{aligned} & A _{11}=0, A _{12}=-(9+2)=-11, A _{13}=0 \\ & A _{21}=-(-3-0)=3, A _{22}=3-2=1, A _{23}=-(0+1)=-1 \\ & A _{31}=2-0=2, A _{32}=-(-2-6)=8, A _{33}=0+3=3 \end{aligned} $

$\therefore adj A= \begin{cases} 0 & 3 & 2 \\ -11 & 1 & 8 \\ 0 & -1 & 3 \end{cases} $

Now,

$ \begin{aligned} A(adj A) & = \begin{bmatrix} 1 & -1 & 2 \\ 3 & 0 & -2 \\ 1 & 0 & 3 \end{bmatrix} \begin{bmatrix} 0 & 3 & 2 \\ -11 & 1 & 8 \\ 0 & -1 & 3 \end{bmatrix} \\ & = \begin{bmatrix} 0+11+0 & 3-1-2 & 2-8+6 \\ 0+0+0 & 9+0+2 & 6+0-6 \\ 0+0+0 & 3+0-3 & 2+0+9 \end{bmatrix} \\ & = \begin{bmatrix} 11 & 0 & 0 \\ 0 & 11 & 0 \\ 0 & 0 & 11 \end{bmatrix} \end{aligned} $

Also,

$ \begin{aligned} (adj A) \cdot A & = \begin{bmatrix} 0 & 3 & 2 \\ -11 & 1 & 8 \\ 0 & -1 & 3 \end{bmatrix} \begin{bmatrix} 1 & -1 & 2 \\ 3 & 0 & -2 \\ 1 & 0 & 3 \end{bmatrix} \\ & = \begin{bmatrix} 0+9+2 & 0+0+0 & 0-6+6 \\ -11+3+8 & 11+0+0 & -22-2+24 \\ 0-3+3 & 0+0+0 & 0+2+9 \end{bmatrix} \\ & = \begin{bmatrix} 11 & 0 & 0 \\ 0 & 11 & 0 \\ 0 & 0 & 11 \end{bmatrix} \end{aligned} $

Hence, $A(adj A)=(adj A) A=|A| I$.

Find the inverse of each of the matrices (if it exists) given in Exercises 5 to 11.

5. $\begin{vmatrix}2 & -2 \\ 4 & 3\end{vmatrix}$

Solution

$|A|=2 \times 3-4 \times-2=14$

Minors are $M_{11}=3 M_{12}=4 M_{21}=-2 M_{22}=2$

Cofactors are $C_{11}=3 C_{12}=-4 C_{21}=2 C_{22}=2$

Adj. $A=\left[\begin{array}{cc}3 & 2 \\ -4 & 2\end{array}\right]$

$A^{-1}=\frac{1}{|A|} A d j . A=\frac{1}{14}\left[\begin{array}{cc} 3 & 2 \\ -4 & 2 \end{array}\right]$

6. $\begin{vmatrix}-1 & 5 \\ -3 & 2\end{vmatrix}$

Solution

Let $A= \begin{vmatrix} -1 & 5 \\ -3 & 2 \end{vmatrix} $.

we have,

$|A|=-2+15=13$

Now,

$A _{11}=2, A _{12}=3, A _{21}=-5, A _{22}=-1$

$\therefore adj A= \begin{vmatrix} 2 & -5 \\ 3 & -1 \end{vmatrix} $

$\therefore A^{-1}=\frac{1}{|A|} adj A=\frac{1}{13} \begin{vmatrix} 2 & -5 \\ 3 & -1 \end{vmatrix} $

7. $\begin{vmatrix}1 & 2 & 3 \\0 & 2 & 4\\0 & 0 & 5 \end{vmatrix}$

Solution

Let $A= \begin{vmatrix} 1 & 2 & 3 \\ 0 & 2 & 4 \\ 0 & 0 & 5 \end{vmatrix} $.

We have,

$|A|=1(10-0)-2(0-0)+3(0-0)=10$

Now,

$A _{11}=10-0=10, A _{12}=-(0-0)=0, A _{13}=0-0=0$

$A _{21}=-(10-0)=-10, A _{22}=5-0=5, A _{23}=-(0-0)=0$

$A _{31}=8-6=2, A _{32}=-(4-0)=-4, A _{33}=2-0=2$

$\therefore adj A= \begin{vmatrix} 10 & -10 & 2 \\ 0 & 5 & -4 \\ 0 & 0 & 2 \end{vmatrix} $

$\therefore A^{-1}=\frac{1}{|A|} adj A=\frac{1}{10} \begin{vmatrix} 10 & -10 & 2 \\ 0 & 5 & -4 \\ 0 & 0 & 2 \end{vmatrix} $

8. $\begin{vmatrix}1 & 0 & 0\\ 3 & 3 & 0\\ 5 & 2 & -1\end{vmatrix}$

Solution

Let $A= \begin{vmatrix} 1 & 0 & 0 \\ 3 & 3 & 0 \\ 5 & 2 & -1 \end{vmatrix} $.

We have,

$|A|=1(-3-0)-0+0=-3$

Now,

$A _{11}=-3-0=-3, A _{12}=-(-3-0)=3, A _{13}=6-15=-9$

$A _{21}=-(0-0)=0, A _{22}=-1-0=-1, A _{23}=-(2-0)=-2$

$A _{31}=0-0=0, A _{32}=-(0-0)=0, A _{33}=3-0=3$

$\therefore adj A= \begin{vmatrix} -3 & 0 & 0 \\ 3 & -1 & 0 \\ -9 & -2 & 3 \end{vmatrix} $

$\therefore A^{-1}=\frac{1}{|A|}$ adj $A=-\frac{1}{3} \begin{vmatrix} -3 & 0 & 0 \\ 3 & -1 & 0 \\ -9 & -2 & 3 \end{vmatrix} $

9. $\begin{vmatrix}2 & 1 & 3\\ 4 & -1 & 0\\ -7 & 2 & 1\end{vmatrix}$

Solution

Let $A= \begin{vmatrix} 2 & 1 & 3 \\ 4 & -1 & 0 \\ -7 & 2 & 1 \end{vmatrix} $.

We have,

$ \begin{aligned} |A| & =2(-1-0)-1(4-0)+3(8-7) \\ & =2(-1)-1(4)+3(1) \\ & =-2-4+3 \\ & =-3 \end{aligned} $

Now,

$ \begin{aligned} & A _{11}=-1-0=-1, A _{12}=-(4-0)=-4, A _{13}=8-7=1 \\ & A _{21}=-(1-6)=5, A _{22}=2+21=23, A _{23}=-(4+7)=-11 \\ & A _{31}=0+3=3, A _{32}=-(0-12)=12, A _{33}=-2-4=-6 \\ & \therefore \text{ adj } A= \begin{bmatrix} -1 & 5 & 3 \\ -4 & 23 & 12 \\ 1 & -11 & -6 \end{bmatrix} \\ & \therefore A^{-1}=\frac{1}{|A|} \text{ adjA }=-\frac{1}{3} \begin{bmatrix} -1 & 5 & 3 \\ -4 & 23 & 12 \\ 1 & -11 & -6 \end{bmatrix} \end{aligned} $

10. $\begin{vmatrix}1 & -1 & 2\\ 0 & 2 & -3\\ 3 & -2 & 4\end{vmatrix}$

Solution

Let $A= \begin{vmatrix} 1 & -1 & 2 \\ 0 & 2 & -3 \\ 3 & -2 & 4 \end{vmatrix} $.

By expanding along $C_1$, we have:

$|A|=1(8-6)-0+3(3-4)=2-3=-1$

Now,

$A _{11}=8-6=2, A _{12}=-(0+9)=-9, A _{13}=0-6=-6$

$A _{21}=-(-4+4)=0, A _{22}=4-6=-2, A _{23}=-(-2+3)=-1$

$A _{31}=3-4=-1, A _{32}=-(-3-0)=3, A _{33}=2-0=2$

$\therefore adj A= \begin{vmatrix} 2 & 0 & -1 \\ -9 & -2 & 3 \\ -6 & -1 & 2 \end{vmatrix} $

$\therefore A^{-1}=\frac{1}{|A|}$ adj $A=- \begin{vmatrix} 2 & 0 & -1 \\ -9 & -2 & 3 \\ -6 & -1 & 2\end{vmatrix} = \begin{vmatrix} -2 & 0 & 1 \\ 9 & 2 & -3 \\ 6 & 1 & -2 \end{vmatrix} $

11. $\begin{vmatrix}1 & 0 & 0 \\ 0 & \cos \alpha & \sin \alpha \\ 0 & \sin \alpha & -\cos \alpha\end{vmatrix}$

Solution

Let $A= \begin{vmatrix} 1 & 0 & 0 \\ 0 & \cos \alpha & \sin \alpha \\ 0 & \sin \alpha & -\cos \alpha \end{vmatrix} $.

We have,

$|A|=1(-\cos ^{2} \alpha-\sin ^{2} \alpha)=-(\cos ^{2} \alpha+\sin ^{2} \alpha)=-1$

Now,

$A _{11}=-\cos ^{2} \alpha-\sin ^{2} \alpha=-1, A _{12}=0, A _{13}=0$

$A _{21}=0, A _{22}=-\cos \alpha, A _{23}=-\sin \alpha$

$A _{31}=0, A _{32}=-\sin \alpha, A _{33}=\cos \alpha$

$\therefore adj A= \begin{vmatrix} -1 & 0 & 0 \\ 0 & -\cos \alpha & -\sin \alpha \\ 0 & -\sin \alpha & \cos \alpha \end{vmatrix} $

$\therefore A^{-1}=\frac{1}{|A|} \cdot adj A=- \begin{vmatrix} -1 & 0 & 0 \\ 0 & -\cos \alpha & -\sin \alpha \\ 0 & -\sin \alpha & \cos \alpha\end{vmatrix} = \begin{vmatrix} 1 & 0 & 0 \\ 0 & \cos \alpha & \sin \alpha \\ 0 & \sin \alpha & -\cos \alpha \end{vmatrix} $

12. Let $A=\begin{vmatrix}3 & 7 \\ 2 & 5\end{vmatrix}$ and $B=\begin{vmatrix}6 & 8 \\ 7 & 9\end{vmatrix}$. Verify that $(A B)^{-1}=B^{-1} A^{-1}$.

Solution

Let $A= \begin{vmatrix} 3 & 7 \\ 2 & 5 \end{vmatrix} $.

We have,

$|A|=15-14=1$

Now,

$A _{11}=5, A _{12}=-2, A _{21}=-7, A _{22}=3$

$\therefore adj A= \begin{vmatrix} 5 & -7 \\ -2 & 3 \end{vmatrix} $

$\therefore A^{-1}=\frac{1}{|A|} \cdot adj A= \begin{vmatrix} 5 & -7 \\ -2 & 3 \end{vmatrix} $

Now, let $B= \begin{vmatrix} 6 & 8 \\ 7 & 9 \end{vmatrix} $.

We have,

$|B|=54-56=-2$

$\therefore adj B= \begin{vmatrix} 9 & -8 \\ -7 & 6 \end{vmatrix} $

$\therefore B^{-1}=\frac{1}{|B|} adj B=-\frac{1}{2} \begin{vmatrix} 9 & -8 \\ -7 & 6\end{vmatrix} = \begin{vmatrix} -\frac{9}{2} & 4 \\ \frac{7}{2} & -3 \end{vmatrix} $

Now,

$$ \begin{align*} B^{-1} A^{-1} & = \begin{bmatrix} -\frac{9}{2} & 4 \\ \frac{7}{2} & -3 \end{bmatrix} \begin{bmatrix} 5 & -7 \\ -2 & 3 \end{bmatrix} \\ & = \begin{bmatrix} -\frac{45}{2}-8 & \frac{63}{2}+12 \\ \frac{35}{2}+6 & -\frac{49}{2}-9 \end{bmatrix} = \begin{bmatrix} -\frac{61}{2} & \frac{87}{2} \\ \frac{47}{2} & -\frac{67}{2} \end{bmatrix} \tag{1} \end{align*} $$

Then,

$ \begin{aligned} A B & = \begin{bmatrix} 3 & 7 \\ 2 & 5 \end{bmatrix} \begin{bmatrix} 6 & 8 \\ 7 & 9 \end{bmatrix} \\ & = \begin{bmatrix} 18+49 & 24+63 \\ 12+35 & 16+45 \end{bmatrix} \\ & = \begin{bmatrix} 67 & 87 \\ 47 & 61 \end{bmatrix} \end{aligned} $

Therefore, we have $|A B|=67 \times 61-87 \times 47=4087-4089=-2$.

Also,

$$ \begin{align*} & adj(A B)= \begin{bmatrix} 61 & -87 \\ -47 & 67 \end{bmatrix} \\ & \begin{align*} \therefore(A B)^{-1}=\frac{1}{|A B|} adj(A B) & =-\frac{1}{2} \begin{bmatrix} 61 & -87 \\ -47 & 67 \end{bmatrix} \\ & = \begin{bmatrix} -\frac{61}{2} & \frac{87}{2} \\ \frac{47}{2} & -\frac{67}{2} \end{bmatrix} . \end{align*} \end{align*} $$

From (1) and (2), we have:

$(A B)^{-1}=B^{-1} A^{-1}$

Hence, the given result is proved.

13. If $A=\begin{vmatrix}3 & 1 \\ -1 & 2\end{vmatrix}$, show that $A^{2}-5 A+7 I=O$. Hence find $A^{-1}$.

Solution

$A= \begin{vmatrix} 3 & 1 \\ -1 & 2 \end{vmatrix} $

$A^{2}=A \cdot A= \begin{vmatrix} 3 & 1 \\ -1 & 2\end{vmatrix} \begin{vmatrix} 3 & 1 \\ -1 & 2\end{vmatrix} = \begin{vmatrix} 9-1 & 3+2 \\ -3-2 & -1+4\end{vmatrix} = \begin{vmatrix} 8 & 5 \\ -5 & 3 \end{vmatrix} $

$\therefore A^{2}-5 A+7 I$

$= \begin{vmatrix} 8 & 5 \\ -5 & 3\end{vmatrix} -5 \begin{vmatrix} 3 & 1 \\ -1 & 2\end{vmatrix} +7 \begin{vmatrix} 1 & 0 \\ 0 & 1 \end{vmatrix} $

$= \begin{vmatrix} 8 & 5 \\ -5 & 3\end{vmatrix} - \begin{vmatrix} 15 & 5 \\ -5 & 10\end{vmatrix} + \begin{vmatrix} 7 & 0 \\ 0 & 7 \end{vmatrix} $

$= \begin{vmatrix} -7 & 0 \\ 0 & -7\end{vmatrix} + \begin{vmatrix} 7 & 0 \\ 0 & 7\end{vmatrix} = \begin{vmatrix} 0 & 0 \\ 0 & 0 \end{vmatrix} $

Hence, $A^{2}-5 A+7 I=O$.

$\therefore A \cdot A-5 A=-7 I$

$\Rightarrow A \cdot A(A^{-1})-5 A A^{-1}=-7 I A^{-1} \quad[.$ Post-multiplying by $A^{-1}$ as $.|A| \neq 0]$

$\Rightarrow A(A A^{-1})-5 I=-7 A^{-1}$

$\Rightarrow A I-5 I=-7 A^{-1}$

$\Rightarrow A^{-1}=-\frac{1}{7}(A-5 I)$

$\Rightarrow A^{-1}=\frac{1}{7}(5 I-A)$

$=\frac{1}{7}( \begin{vmatrix} 5 & 0 \\ 0 & 5\end{vmatrix} - \begin{vmatrix} 3 & 1 \\ -1 & 2\end{vmatrix} )=\frac{1}{7} \begin{vmatrix} 2 & -1 \\ 1 & 3 \end{vmatrix} $

$\therefore A^{-1}=\frac{1}{7} \begin{vmatrix} 2 & -1 \\ 1 & 3 \end{vmatrix} $

14. For the matrix $A=\begin{vmatrix}3 & 2 \\ 1 & 1\end{vmatrix}$, find the numbers $a$ and $b$ such that $A^{2}+a A+b I=O$.

Solution

$A= \begin{vmatrix} 3 & 2 \\ 1 & 1 \end{vmatrix} $

$\therefore A^{2}= \begin{vmatrix} 3 & 2 \\ 1 & 1\end{vmatrix} \begin{vmatrix} 3 & 2 \\ 1 & 1\end{vmatrix} = \begin{vmatrix} 9+2 & 6+2 \\ 3+1 & 2+1\end{vmatrix} = \begin{vmatrix} 11 & 8 \\ 4 & 3 \end{vmatrix} $

Now,

$A^{2}+a A+b I=O$

$\Rightarrow(A A) A^{-1}+a A A^{-1}+b I A^{-1}=O \quad \quad[$ Post-multiplying by $A^{-1}$ as $.|A| \neq 0]$

$\Rightarrow A(A A^{-1})+a I+b(I A^{-1})=O$

$\Rightarrow A I+a I+b A^{-1}=O$

$\Rightarrow A+a I=-b A^{-1}$

$\Rightarrow A^{-1}=-\frac{1}{b}(A+a I)$

Now,

$A^{-1}=\frac{1}{|A|}$ adj $A=\frac{1}{1} \begin{vmatrix} 1 & -2 \\ -1 & 3\end{vmatrix} = \begin{vmatrix} 1 & -2 \\ -1 & 3 \end{vmatrix} $

We have:

$ \begin{vmatrix} 1 & -2 \\ -1 & 3\end{vmatrix} =-\frac{1}{b}( \begin{vmatrix} 3 & 2 \\ 1 & 1\end{vmatrix} + \begin{vmatrix} a & 0 \\ 0 & a\end{vmatrix} )=-\frac{1}{b} \begin{vmatrix} 3+a & 2 \\ 1 & 1+a\end{vmatrix} = \begin{vmatrix} \frac{-3-a}{b} & -\frac{2}{b} \\ -\frac{1}{b} & \frac{-1-a}{b} \end{vmatrix} $

Comparing the corresponding elements of the two matrices, we have:

$-\frac{1}{b}=-1 \Rightarrow b=1$

$\frac{-3-a}{b}=1 \Rightarrow-3-a=1 \Rightarrow a=-4$

Hence, -4 and 1 are the required values of $a$ and $b$ respectively.

15. For the matrix $A=\begin{vmatrix}1 & 1 & 1\\ 1 & 2 & -3\\ 2 & -1 & 3\end{vmatrix}$

Show that $A^{3}-6 A^{2}+5 A+11 I=O$. Hence, find $A^{-1}$.

Solution

$ \begin{aligned} & A= \begin{bmatrix} 1 & 1 & 1 \\ 1 & 2 & -3 \\ 2 & -1 & 3 \end{bmatrix} \\ & A^{2}= \begin{bmatrix} 1 & 1 & 1 \\ 1 & 2 & -3 \\ 2 & -1 & 3 \end{bmatrix} \begin{bmatrix} 1 & 1 & 1 \\ 1 & 2 & -3 \\ 2 & -1 & 3 \end{bmatrix} \end{aligned} $

$= \begin{bmatrix} 1+1+2 & 1+2-1 & 1-3+3 \\ 1+2-6 & 1+4+3 & 1-6-9 \\ 2-1+6 & 2-2-3 & 2+3+9 \end{bmatrix}$

$= \begin{bmatrix} 4 & 2 & 1 \\ -3 & 8 & -14 \\ 7 & -3 & 14 \end{bmatrix}$

$ \begin{aligned} & A^{3}=A^{2} \cdot A= \begin{bmatrix} 4 & 2 & 1 \\ -3 & 8 & -14 \\ 7 & -3 & 14 \end{bmatrix} \begin{bmatrix} 1 & 1 & 1 \\ 1 & 2 & -3 \\ 2 & -1 & 3 \end{bmatrix} \\ & = \begin{bmatrix} 4+2+2 & 4+4-1 & 4-6+3 \\ -3+8-28 & -3+16+14 & -3-24-42 \\ 7-3+28 & 7-6-14 & 7+9+42 \end{bmatrix} \\ & = \begin{bmatrix} 8 & 7 & 1 \\ -23 & 27 & -69 \\ 32 & -13 & 58 \end{bmatrix} \end{aligned} $

$\therefore A^{3}-6 A^{2}+5 A+11 I$

$= \begin{bmatrix} 8 & 7 & 1 \\ -23 & 27 & -69 \\ 32 & -13 & 58\end{bmatrix} -6 \begin{bmatrix} 4 & 2 & 1 \\ -3 & 8 & -14 \\ 7 & -3 & 14\end{bmatrix} +5 \begin{bmatrix} 1 & 1 & 1 \\ 1 & 2 & -3 \\ 2 & -1 & 3\end{bmatrix} +11 \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} $

$= \begin{bmatrix} 8 & 7 & 1 \\ -23 & 27 & -69 \\ 32 & -13 & 58\end{bmatrix} - \begin{bmatrix} 24 & 12 & 6 \\ -18 & 48 & -84 \\ 42 & -18 & 84\end{bmatrix} + \begin{bmatrix} 5 & 5 & 5 \\ 5 & 10 & -15 \\ 10 & -5 & 15\end{bmatrix} + \begin{bmatrix} 11 & 0 & 0 \\ 0 & 11 & 0 \\ 0 & 0 & 11 \end{bmatrix} $

$= \begin{bmatrix} 24 & 12 & 6 \\ -18 & 48 & -84 \\ 42 & -18 & 84\end{bmatrix} - \begin{bmatrix} 24 & 12 & 6 \\ -18 & 48 & -84 \\ 42 & -18 & 84 \end{bmatrix} $

$= \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} =O$

Thus, $A^{3}-6 A^{2}+5 A+11 I=O$.

Now,

$A^{3}-6 A^{2}+5 A+11 I=O$

$\Rightarrow(A A A) A^{-1}-6(A A) A^{-1}+5 A A^{-1}+11 I A^{-1}=0 \quad[.$ Post-multiplying by $A^{-1}$ as $|A| \neq 0$ ]

$\Rightarrow A A(A A^{-1})-6 A(A A^{-1})+5(A A^{-1})=-11(I A^{-1})$

$\Rightarrow A^{2}-6 A+5 I=-11 A^{-1}$

$\Rightarrow A^{-1}=-\frac{1}{11}(A^{2}-6 A+5 I)$

Now,

$ \begin{aligned} & A^{2}-6 A+5 I \\ & = \begin{bmatrix} 4 & 2 & 1 \\ -3 & 8 & -14 \\ 7 & -3 & 14 \end{bmatrix} -6 \begin{bmatrix} 1 & 1 & 1 \\ 1 & 2 & -3 \\ 2 & -1 & 3 \end{bmatrix} +5 \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \\ & = \begin{bmatrix} 4 & 2 & 1 \\ -3 & 8 & -14 \\ 7 & -3 & 14 \end{bmatrix} - \begin{bmatrix} 6 & 6 & 6 \\ 6 & 12 & -18 \\ 12 & -6 & 18 \end{bmatrix} + \begin{bmatrix} 5 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 5 \end{bmatrix} \\ & = \begin{bmatrix} 9 & 2 & 1 \\ -3 & 13 & -14 \\ 7 & -3 & 19 \end{bmatrix} - \begin{bmatrix} 6 & 6 & 6 \\ 6 & 12 & -18 \\ 12 & -6 & 18 \end{bmatrix} \\ & = \begin{bmatrix} 3 & -4 & -5 \\ -9 & 1 & 4 \\ -5 & 3 & 1 \end{bmatrix} \end{aligned} $

From equation (1), we have:

$ A^{-1}=-\frac{1}{11} \begin{bmatrix} 3 & -4 & -5 \\ -9 & 1 & 4 \\ -5 & 3 & 1 \end{bmatrix} =\frac{1}{11} \begin{bmatrix} -3 & 4 & 5 \\ 9 & -1 & -4 \\ 5 & -3 & -1 \end{bmatrix} $

16. If $A=\begin{vmatrix}2 & -1 & 1\\ -1 & 2 & -1\\ 1 & -1 & 2\end{vmatrix}$

Verify that $A^{3}-6 A^{2}+9 A-4 I=O$ and hence find $A^{-1}$

Solution

$$ \begin{aligned} & A= \begin{bmatrix} 2 & -1 & 1 \\ -1 & 2 & -1 \\ 1 & -1 & 2 \end{bmatrix} \\ & .A^{2}=\begin{bmatrix} { \begin{bmatrix} 2 \\ -1 \\ 1 \end{bmatrix} .} & \begin{bmatrix} -1 \\ 2 \\ -1 \end{bmatrix} & .\begin{bmatrix} 1 \\ -1 \\ 2 \end{bmatrix} \end{bmatrix} \begin{bmatrix} 2 & -1 & 1 \\ -1 \\ 1 & 2 & -1 \\ -1 & 2 \end{bmatrix} \\ & = \begin{bmatrix} 4+1+1 & -2-2-1 & 2+1+2 \\ -2-2-1 & 1+4+1 & -1-2-2 \\ 2+1+2 & -1-2-2 & 1+1+4 \end{bmatrix} \\ & = \begin{bmatrix} 6 & -5 & 5 \\ -5 & 6 & -5 \\ 5 & -5 & 6 \end{bmatrix} \\ & A^{3}=A^{2} A= \begin{bmatrix} 6 & -5 & 5 \\ -5 & 6 & -5 \\ 5 & -5 & 6 \end{bmatrix} \begin{bmatrix} 2 & -1 & 1 \\ -1 & 2 & -1 \\ 1 & -1 & 2 \end{bmatrix} \\ & = \begin{bmatrix} 12+5+5 & -6-10-5 & 6+5+10 \\ -10-6-5 & 5+12+5 & -5-6-10 \\ 10+5+6 & -5-10-6 & 5+5+12 \end{bmatrix} \\ & = \begin{bmatrix} 22 & -21 & 21 \\ -21 & 22 & -21 \\ 21 & -21 & 22 \end{bmatrix} \end{aligned} $$

Now,

$ \begin{aligned} & A^{3}-6 A^{2}+9 A-4 I \\ & = \begin{bmatrix} 22 & -21 & 21 \\ -21 & 22 & -21 \\ 21 & -21 & 22 \end{bmatrix} -6 \begin{bmatrix} 6 & -5 & 5 \\ -5 & 6 & -5 \\ 5 & -5 & 6 \end{bmatrix} +9 \begin{bmatrix} 2 & -1 & 1 \\ -1 & 2 & -1 \\ 1 & -1 & 2 \end{bmatrix} -4 \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \\ & = \begin{bmatrix} 22 & -21 & 21 \\ -21 & 22 & -21 \\ 21 & -21 & 22 \end{bmatrix} - \begin{bmatrix} 36 & -30 & 30 \\ -30 & 36 & -30 \\ 30 & -30 & 36 \end{bmatrix} + \begin{bmatrix} 18 & -9 & 9 \\ -9 & 18 & -9 \\ 9 & -9 & 18 \end{bmatrix} - \begin{bmatrix} 4 & 0 & 0 \\ 0 & 4 & 0 \\ 0 & 0 & 4 \end{bmatrix} \\ & = \begin{bmatrix} 40 & -30 & 30 \\ -30 & 40 & -30 \\ 30 & -30 & 40 \end{bmatrix} - \begin{bmatrix} 40 & -30 & 30 \\ -30 & 40 & -30 \\ 30 & -30 & 40 \end{bmatrix} = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} \end{aligned} $

$\therefore A^{3}-6 A^{2}+9 A-4 I=O$

Now,

$$ \begin{align*} & A^{3}-6 A^{2}+9 A-4 I=O \\ & \Rightarrow(A A A) A^{-1}-6(A A) A^{-1}+9 A A^{-1}-4 I A^{-1}=O \\ & \Rightarrow A A(A A^{-1})-6 A(A A^{-1})+9(A A^{-1})=4(I A^{-1}) \\ & \Rightarrow A A I-6 A I+9 I=4 A^{-1} \\ & \Rightarrow A^{2}-6 A+9 I=4 A^{-1} \tag{1}\\ & \Rightarrow A^{-1}=\frac{1}{4}(A^{2}-6 A+9 I) \end{align*} $$

$ \Rightarrow(A A A) A^{-1}-6(A A) A^{-1}+9 A A^{-1}-4 I A^{-1}=O \quad \quad[\text{ Post-multiplying by } A^{-1} \text{ as }|A| \neq 0] $

$A^{2}-6 A+9 I$

$= \begin{bmatrix} 6 & -5 & 5 \\ -5 & 6 & -5 \\ 5 & -5 & 6\end{bmatrix} -6 \begin{bmatrix} 2 & -1 & 1 \\ -1 & 2 & -1 \\ 1 & -1 & 2\end{bmatrix} +9 \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} $

$= \begin{bmatrix} 6 & -5 & 5 \\ -5 & 6 & -5 \\ 5 & -5 & 6\end{bmatrix} - \begin{bmatrix} 12 & -6 & 6 \\ -6 & 12 & -6 \\ 6 & -6 & 12\end{bmatrix} + \begin{bmatrix} 9 & 0 & 0 \\ 0 & 9 & 0 \\ 0 & 0 & 9 \end{bmatrix} $

$= \begin{bmatrix} 3 & 1 & -1 \\ 1 & 3 & 1 \\ -1 & 1 & 3 \end{bmatrix} $

From equation (1), we have:

$ A^{-1}=\frac{1}{4} \begin{bmatrix} 3 & 1 & -1 \\ 1 & 3 & 1 \\ -1 & 1 & 3 \end{bmatrix} $

17. Let $A$ be a nonsingular square matrix of order $3 \times 3$. Then $|adj A|$ is equal to

(A) $|A|$

(B) $|A|^{2}$

(C) $|A|^{3}$

(D) $3|A|$

Solution

We know that,

$(adj A) A=|A| I= \begin{bmatrix} |A| & 0 & 0 \\ 0 & |A| & 0 \\ 0 & 0 & |A| \end{bmatrix} $

$\Rightarrow|(adj A) A|= \begin{vmatrix} |A| & 0 & 0 \\ 0 & |A| & 0 \\ 0 & 0 & |A|\end{vmatrix} $

$\Rightarrow|adj A||A|=|A|^{3} \begin{vmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{vmatrix} =|A|^{3}(I)$

$\therefore|adj A|=|A|^{2}$

Hence, the correct answer is B.

18. If $A$ is an invertible matrix of order 2 , then $det(A^{-1})$ is equal to

(A) $det(A)$

(B) $\frac{1}{det(A)}$

(C) 1

(D) 0

Solution

Since $A$ is an invertible matrix, $A^{-1}$ exists and $A^{-1}=\frac{1}{|A|}$ adj $A$.

As matrix $A$ is of order 2, let $A= \begin{vmatrix} a & b \\ c & d \end{vmatrix} $.

Then, $|A|=a d-b c$ and $a d j A= \begin{vmatrix} d & -b \\ -c & a \end{vmatrix}$.

Now,

$ \begin{aligned} & A^{-1}=\frac{1}{|A|} \text{ adj } A= \begin{vmatrix} \frac{d}{|A|} & \frac{-b}{|A|} \\ \frac{-c}{|A|} & \frac{a}{|A|} \end{vmatrix} \\ & \therefore|A^{-1}|= \begin{vmatrix} \frac{d}{|A|} & \frac{-b}{|A|} \\ \frac{-c}{|A|} & \frac{a}{|A|} \end{vmatrix} =\frac{1}{|A|^{2}} \begin{vmatrix} d & -b \\ -c & a \end{vmatrix} =\frac{1}{|A|^{2}}(a d-b c)=\frac{1}{|A|^{2}} \cdot|A|=\frac{1}{|A|} \\ & \therefore det(A^{-1})=\frac{1}{det(A)} \end{aligned} $

Hence, the correct answer is B.

Applications of Determinants and Matrices

In this section, we shall discuss application of determinants and matrices for solving the system of linear equations in two or three variables and for checking the consistency of the system of linear equations.

Consistent system A system of equations is said to be consistent if its solution (one or more) exists.

Inconsistent system A system of equations is said to be inconsistent if its solution does not exist.

Note In this chapter, we restrict ourselves to the system of linear equations having unique solutions only.

4.6.1 Solution of system of linear equations using inverse of a matrix

Let us express the system of linear equations as matrix equations and solve them using inverse of the coefficient matrix.

Consider the system of equations

$ \begin{gathered} a_1 x+b_1 y+c_1 z=d_1 \\ a_2 x+b_2 y+c_2 z=d_2 \\ a_3 x+b_3 y+c_3 z=d_3 \\ \text{ Let } \quad A=\begin{vmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{vmatrix}, X=\begin{vmatrix} x \\ y \\ z \end{vmatrix} \text{ and } B=\begin{vmatrix} d_1 \\ d_2 \\ d_3 \end{vmatrix} \end{gathered} $

Then, the system of equations can be written as, $AX=B$, i.e.,

$ \begin{vmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{vmatrix}\begin{vmatrix} x \\ y \\ z \end{vmatrix}=\begin{vmatrix} d_1 \\ d_2 \\ d_3 \end{vmatrix} $

Case I If $A$ is a nonsingular matrix, then its inverse exists. Now

$ A X=B $

or

$ \begin{aligned} A^{-1}(AX) & =A^{-1} B \\ (A^{-1} A) X & =A^{-1} B \\ IX & =A^{-1} B \\ X & =A^{-1} B \end{aligned} $ (premultiplying by A–1) (by associative property) $ \text{ or } $

or

This matrix equation provides unique solution for the given system of equations as inverse of a matrix is unique. This method of solving system of equations is known as Matrix Method.

Case II If $A$ is a singular matrix, then $|A|=0$.

In this case, we calculate $(adj A) B$.

If (adj A) B $\neq O$, ( $O$ being zero matrix), then solution does not exist and the system of equations is called inconsistent.

If $(adj A) B=O$, then system may be either consistent or inconsistent according as the system have either infinitely many solutions or no solution.

Example 16 Solve the system of equations

$ \begin{aligned} & 2 x+5 y=1 \\ & 3 x+2 y=7 \end{aligned} $

Solution The system of equations can be written in the form AX = B, where

$ A=\begin{vmatrix} 2 & 5 \\ 3 & 2 \end{vmatrix}, X=\begin{vmatrix} x \\ y \end{vmatrix} \text{ and } B=\begin{vmatrix} 1 \\ 7 \end{vmatrix} $

Now, $|A|=-11 \neq 0$, Hence, $A$ is nonsingular matrix and so has a unique solution.

Note that

$\begin{aligned}A^{-1} & =-\frac{1}{11} \begin{vmatrix} 2 & -5\\ -3 & 2 \end{vmatrix}\end{aligned}$

$ \text {Therefore} \quad\quad\begin{aligned} X & =A^{-1} B=-\frac{1}{11}\begin{vmatrix} 2 & -5 & \\ -3 & 2 \end{vmatrix} \end{aligned}\frac{1}{7} $

$ \text {i.e.} \quad\quad \begin{aligned} \begin{vmatrix} x \\ y \end{vmatrix}=-\frac{1}{11}\begin{vmatrix} -33 \\ 11 \end{vmatrix}=\begin{vmatrix} 3\\ 1 \end{vmatrix} \end{aligned} $

Hence $\quad\quad$$ x=3, y=-1

Example 17 Solve the following system of equations by matrix method.

$ \begin{vmatrix}{r} 3 x-2 y+3 z=8 \\ 2 x+y-z=1 \\ 4 x-3 y+2 z=4 \end{vmatrix} $

Solution The system of equations can be written in the form $AX=B$, where

$ A=\begin{vmatrix} 3 & -2 & 3 \\ 2 & 1 & -1 \\ 4 & -3 & 2 \end{vmatrix}, X=\begin{vmatrix} x \\ y \\ z \end{vmatrix} \text{ and } B=\begin{vmatrix} 8 \\ 1 \\ 4 \end{vmatrix} $

We see that

$ |A|=3(2-3)+2(4+4)+3(-6-4)=-17 \neq 0 $

Hence, $A$ is nonsingular and so its inverse exists. Now $A _{11}=-1$, $A _{12}=-8$, $A _{13}=-10$ $A _{21}=-5$ $A _{22}=-6$, $A _{23}=1$ $A _{31}=-1$, $A _{32}=9$, $A _{33}=7$

Therefore

$ \begin{aligned} & A^{-1}=-\frac{1}{17}\begin{vmatrix} -1 & -5 & -1 \\ -8 & -6 & 9 \\ -10 & 1 & 7 \end{vmatrix} \\ & X=A^{-1} B=-\frac{1}{17}\begin{vmatrix} -1 & -5 & -1 \\ -8 & -6 & 9 \\ -10 & 1 & 7 \end{vmatrix}\begin{vmatrix} 8 \\ 1 \\ 4 \end{vmatrix} \\ & {\begin{vmatrix}{l} x \\ y \\ z \end{vmatrix}=-\frac{1}{17}\begin{vmatrix}{l} -17 \\ -34 \\ -51 \end{vmatrix}=\begin{vmatrix} 2 \\ 3 \end{vmatrix} } \end{aligned} $

Hence

$ x=1, y=2 \text{ and } z=3 \text{. } $

Example 18 ** The sum of three numbers is 6 . If we multiply third number by 3 and add second number to it, we get 11 . By adding first and third numbers, we get double of the second number. Represent it algebraically and find the numbers using matrix method.

Solution Let first, second and third numbers be denoted by $x, y$ and $z$, respectively. Then, according to given conditions, we have

$ \begin{aligned} x+y+z & =6 \\ y+3 z & =11 \\ x+z & =2 y \text{ or } x-2 y+z=0 \end{aligned} $

This system can be written as $AX=B$, where

$ A=\begin{vmatrix} 1 & 1 & 1 \\ 0 & 1 & 3 \\ 1 & 2 & 1 \end{vmatrix}, X=\begin{gathered} x \\ y \\ z \end{gathered} \text{ and } B=\begin{gathered} 6 \\ 11 \\ 0 \end{gathered} $

Here $|A|=1(1+6)-(0-3)+(0-1)=9 \neq 0$. Now we find $adj A$

$ \begin{vmatrix} A _{11}=1(1+6)=7, & A _{12}=-(0-3)=3, & A _{13}=-1 \\ A _{21}=-(1+2)=-3, & A _{22}=0, & A _{23}=-(-2-1)=3 \\ A _{31}=(3-1)=2, & A _{32}=-(3-0)=-3, & A _{33}=(1-0)=1 \\ & \text{ adj } A=\begin{vmatrix} 7 & -3 & 2 \\ 3 & 0 & -3 \\ -1 & 3 & 1 \end{vmatrix} \end{vmatrix} $

Hence

Thus

Since

or

Thus

$ A^{-1}=\frac{1}{|A|} adj(A)=\frac{1}{9}\begin{vmatrix} 7 & -3 & 2 \\ 3 & 0 & -3 \\ -1 & 3 & 1 \end{vmatrix} $

$ X=A^{-1} B $

$ X=\frac{1}{9}\begin{vmatrix} 7 & -3 & 2 \\ 3 & 0 & -3 \\ -1 & 3 & 1 \end{vmatrix}\begin{vmatrix}{c} 6 \\ 11 \\ 0 \end{vmatrix} $

$ \begin{aligned} & x \\ & y \\ & z \end{aligned}=\frac{1}{9}\begin{vmatrix}{l} 42-33+0 \\ 18+0+0 \\ -6+33+0 \end{vmatrix}=\frac{1}{9} \quad \begin{gathered} 9 \\ 27 \end{gathered}=\begin{aligned} & 1 \\ & 3 \end{aligned} $

$ x=1, y=2, z=3 $

EXERCISE 4.5

Examine the consistency of the system of equations in Exercises 1 to 6.

1. $x+2 y=2$

$\quad\quad$$2 x+3 y=3$

Solution

The given system of equations is:

$x+2 y=2$

$2 x+3 y=3$

The given system of equations can be written in the form of $A X=B$, where

$A= \begin{bmatrix} 1 & 2 \\ 2 & 3\end{bmatrix} , X= \begin{bmatrix} x \\ y\end{bmatrix} $ and $B= \begin{bmatrix} 2 \\ 3 \end{bmatrix} $.

Now,

$|A|=1(3)-2(2)=3-4=-1 \neq 0$

$\therefore A$ is non-singular.

Therefore, $A^{-1}$ exists.

Hence, the given system of equations is consistent.

2. $2 x-y=5$

$\quad\quad$$x+y=4$

Solution

The given system of equations is:

$2 x-y=5$

$x+y=4$

The given system of equations can be written in the form of $A X=B$, where

$A= \begin{bmatrix} 2 & -1 \\ 1 & 1\end{bmatrix} , X= \begin{bmatrix} x \\ z\end{bmatrix} $ and $B= \begin{bmatrix} 5 \\ 4 \end{bmatrix} $.

Now,

$|A|=2(1)-(-1)(1)=2+1=3 \neq 0$

$\therefore A$ is non-singular.

Therefore, $A^{-1}$ exists.

Hence, the given system of equations is consistent.

3. $x+3 y=5$

$\quad\quad$$2 x+6 y=8$

Solution

Answer

The given system of equations is:

$x+3 y=5$

$2 x+6 y=8$

The given system of equations can be written in the form of $A X=B$, where

$A= \begin{bmatrix} 1 & 3 \\ 2 & 6\end{bmatrix} , X= \begin{bmatrix} x \\ y\end{bmatrix} $ and $B= \begin{bmatrix} 5 \\ 8 \end{bmatrixs} $.

Now,

$|A|=1(6)-3(2)=6-6=0$

$\therefore A$ is a singular matrix.

Now,

$(adj A)= \begin{bmatrix} 6 & -3 \\ -2 & 1 \end{bmatrix} $

$(adj A) B= \begin{bmatrix} 6 & -3 \\ -2 & 1\end{bmatrix} \begin{bmatrix} 5 \\ 8\end{bmatrix} = \begin{bmatrix} 30-24 \\ -10+8\end{bmatrix} = \begin{bmatrix} 6 \\ -2 \end{bmatrix} \neq O$

Thus, the solution of the given system of equations does not exist. Hence, the system of equations is inconsistent.

4. $x+y+z=1$

$\quad\quad$$2 x+3 y+2 z=2$

$\quad\quad$$a x+a y+2 a z=4$

Solution

The given system of equations is:

$x+y+z=1$

$2 x+3 y+2 z=2$

$a x+a y+2 a z=4$

This system of equations can be written in the form $A X=B$, where

$ A= \begin{bmatrix} 1 & 1 & 1 \\ 2 & 3 & 2 \\ a & a & 2 a \end{bmatrix} , X= \begin{bmatrix} x \\ y \\ z \end{bmatrix} \text{ and } B= \begin{bmatrix} 1 \\ 2 \\ 4 \end{bmatrix} \text{. } $

Now,

$ \begin{aligned} |A| & =1(6 a-2 a)-1(4 a-2 a)+1(2 a-3 a) \\ & =4 a-2 a-a=4 a-3 a=a \neq 0 \end{aligned} $

$\therefore A$ is non-singular.

Therefore, $A^{-1}$ exists.

Hence, the given system of equations is consistent.

5. $3 x-y-2 z=2$

$\quad\quad$$2 y-z=-1$

$\quad\quad$$3 x-5 y=3$

Solution

The given system of equations is:

$3 x-y-2 z=2$

$2 y-z=-1$

$3 x-5 y=3$

This system of equations can be written in the form of $A X=B$, where

$A= \begin{bmatrix} 3 & -1 & -2 \\ 0 & 2 & -1 \\ 3 & -5 & 0\end{bmatrix} , X= \begin{bmatrix} x \\ y \\ z\end{bmatrix} $ and $B= \begin{bmatrix} 2 \\ -1 \\ 3 \end{bmatrix} $.

Now,

$|A|=3(0-5)-0+3(1+4)=-15+15=0$

$\therefore A$ is a singular matrix.

Now,

$(adj A)= \begin{bmatrix} -5 & 10 & 5 \\ -3 & 6 & 3 \\ -6 & 12 & 6 \end{bmatrix} $

$\therefore(adj A) B= \begin{bmatrix} -5 & 10 & 5 \\ -3 & 6 & 3 \\ -6 & 12 & 6\end{bmatrix} \begin{bmatrix} 2 \\ -1 \\ 3\end{bmatrix} = \begin{bmatrix} -10-10+15 \\ -6-6+9 \\ -12-12+18\end{bmatrix} = \begin{bmatrix} -5 \\ -3 \\ -6 \end{bmatrix} \neq O$

Thus, the solution of the given system of equations does not exist. Hence, the system of equations is inconsistent.

6. $5 x-y+4 z=5$

$\quad\quad$$2 x+ 3y+5z=2$

$\quad\quad$$5 x-2 y+6 z=-1$

Solution

The given system of equations is:

$5 x-y+4 z=5$

$2 x+3 y+5 z=2$

$5 x-2 y+6 z=-1$

This system of equations can be written in the form of $A X=B$, where

$A= \begin{bmatrix} 5 & -1 & 4 \\ 2 & 3 & 5 \\ 5 & -2 & 6\end{bmatrix} , X= \begin{bmatrix} x \\ y \\ z\end{bmatrix} $ and $B= \begin{bmatrix} 5 \\ 2 \\ -1 \end{bmatrix} $.

Now,

$$ \begin{aligned} |A| & =5(18+10)+1(12-25)+4(-4-15) \\ & =5(28)+1(-13)+4(-19) \\ & =140-13-76 \\ & =51 \neq 0 \end{aligned} $$

$\therefore A$ is non-singular.

Therefore, $A^{-1}$ exists.

Hence, the given system of equations is consistent.

Solve system of linear equations, using matrix method, in Exercises 7 to 14.

7. $5 x+2 y=4$

$\quad\quad$$7 x+3 y=5$

Solution

The given system of equations can be written in the form of $A X=B$, where

$A= \begin{bmatrix} 5 & 2 \\ 7 & 3\end{bmatrix} , X= \begin{bmatrix} x \\ y\end{bmatrix} $ and $B= \begin{bmatrix} 4 \\ 5 \end{bmatrix} $.

Now, $|A|=15-14=1 \neq 0$.

Thus, $A$ is non-singular. Therefore, its inverse exists.

Now,

$A^{-1}=\frac{1}{|A|}(adj A)$

$\therefore A^{-1}= \begin{bmatrix} 3 & -2 \\ -7 & 5 \end{bmatrix} $

$\therefore X=A^{-1} B= \begin{bmatrix} 3 & -2 \\ -7 & 5\end{bmatrix} \begin{bmatrix} 4 \\ 5 \end{bmatrix} $

$\Rightarrow \begin{bmatrix} x \\ y\end{bmatrix} = \begin{bmatrix} 12-10 \\ -28+25\end{bmatrix} = \begin{bmatrix} 2 \\ -3 \end{bmatrix} $

Hence, $x=2$ and $y=-3$.

8. $2 x-y=-2$

$\quad\quad$$3 x+4 y=3$

Solution

The given system of equations can be written in the form of $A X=B$, where

$A= \begin{bmatrix} 2 & -1 \\ 3 & 4\end{bmatrix} , X= \begin{bmatrix} x \\ y\end{bmatrix} $ and $B= \begin{bmatrix} -2 \\ 3 \end{bmatrix} $.

Now,

$|A|=8+3=11 \neq 0$

Thus, $A$ is non-singular. Therefore, its inverse exists.

Now,

$A^{-1}=\frac{1}{|A|} adj A=\frac{1}{11} \begin{bmatrix} 4 & 1 \\ -3 & 2 \end{bmatrix} $

$\therefore X=A^{-1} B=\frac{1}{11} \begin{bmatrix} 4 & 1 \\ -3 & 2\end{bmatrix} \begin{bmatrix} -2 \\ 3 \end{bmatrix} $

$\Rightarrow \begin{bmatrix} x \\ y\end{bmatrix} =\frac{1}{11} \begin{bmatrix} -8+3 \\ 6+6\end{bmatrix} =\frac{1}{11} \begin{bmatrix} -5 \\ 12\end{bmatrix} = \begin{bmatrix} -\frac{5}{11} \\ \frac{12}{11} \end{bmatrix} $

Hence, $x=\frac{-5}{11}$ and $y=\frac{12}{11}$.

9. $4 x-3 y=3$

$\quad\quad$$3 x-5 y=7$

Solution

The given system of equations can be written in the form of $A X=B$, where

$ A= \begin{bmatrix} 4 & -3 \\ 3 & -5 \end{bmatrix} , X= \begin{bmatrix} x \\ y \end{bmatrix} \text{ and } B= \begin{bmatrix} 3 \\ 7 \end{bmatrix} \text{. } $

Now,

$|A|=-20+9=-11 \neq 0$

Thus, $A$ is non-singular. Therefore, its inverse exists.

Now,

$A^{-1}=\frac{1}{|A|}(adj A)=-\frac{1}{11} \begin{bmatrix} -5 & 3 \\ -3 & 4\end{bmatrix} =\frac{1}{11} \begin{bmatrix} 5 & -3 \\ 3 & -4 \end{bmatrix} $

$\therefore X=A^{-1} B=\frac{1}{11} \begin{bmatrix} 5 & -3 \\ 3 & -4\end{bmatrix} \begin{bmatrix} 3 \\ 7 \end{bmatrix} $

$\Rightarrow \begin{bmatrix} x \\ y\end{bmatrix} =\frac{1}{11} \begin{bmatrix} 5 & -3 \\ 3 & -4\end{bmatrix} \begin{bmatrix} 3 \\ 7\end{bmatrix} =\frac{1}{11} \begin{bmatrix} 15-21 \\ 9-28\end{bmatrix} =\frac{1}{11} \begin{bmatrix} -6 \\ -19\end{bmatrix} = \begin{bmatrix} -\frac{6}{11} \\ -\frac{19}{11} \end{bmatrix} $

Hence, $x=\frac{-6}{11}$ and $y=\frac{-19}{11}$.

10. $5 x+2 y=3$

$\quad\quad$$3 x+2 y=5$

Solution

The given system of equations can be written in the form of $A X=B$, where

$A= \begin{bmatrix} 5 & 2 \\ 3 & 2\end{bmatrix} , X= \begin{bmatrix} x \\ y\end{bmatrix} $ and $B= \begin{bmatrix} 3 \\ 5 \end{bmatrix} $.

Now,

$|A|=10-6=4 \neq 0$

Thus, $A$ is non-singular. Therefore, its inverse exists.

11. $2 x+y+z=1$

$\quad\quad$$x-2 y-z=\frac{3}{2}$

$\quad\quad$$3 y-5 z=9$

Solution

The given system of equations can be written in the form of $A X=B$, where

$A= \begin{bmatrix} 2 & 1 & 1 \\ 1 & -2 & -1 \\ 0 & 3 & -5\end{bmatrix} , X= \begin{bmatrix} x \\ y \\ z \end{bmatrix} $ and $B= \begin{bmatrix} 1 \\ \frac{3}{2} \\ 9 \end{bmatrix} $.

Now,

$|A|=2(10+3)-1(-5-3)+0=2(13)-1(-8)=26+8=34 \neq 0$

Thus, $A$ is non-singular. Therefore, its inverse exists.

$\begin{aligned} & \operatorname{adj}(A)=\left[\begin{array}{lll}A_{11} & A_{12} & A_{13} \\ A_{21} & A_{22} & A_{23} \\ A_{31} & A_{32} & A_{33}\end{array}\right]^{\top} \\ & =\left[\begin{array}{ccc}M_{11} & -M_{21} & M_{31} \\ -M_{12} & M_{22} & -M_{32} \\ M_{13} & -M_{23} & M_{33}\end{array}\right]=\left[\begin{array}{ccc}13 & 8 & 1 \\ 5 & -10 & 3 \\ 3 & -6 & -5 \\ \end{array}\right]\end{aligned}$

$\begin{aligned} & A^{-1}=\frac{1}{|A|} \operatorname{adj} A \\ & =\frac{1}{34}\left[\begin{array}{ccc} 13 & 8 & 1 \\ 5 & -10 & 3 \\ 3 & -6 & -5 \end{array}\right] \end{aligned}$

Solve for the values of $x, y$ and $z$

$A X=B \Rightarrow X=A^{-1} B$

$\begin{aligned} & \Rightarrow\left[\begin{array}{l} x \\ y \\ z \end{array}\right]=\frac{1}{34}\left[\begin{array}{ccc} 13 & 8 & 1 \\ 5 & -10 & 3 \\ 3 & -6 & -5 \end{array}\right]\left[\begin{array}{l} 1 \\ \frac{3}{2} \\ 9 \end{array}\right] \\ & \Rightarrow\left[\begin{array}{l} x \\ y \\ z \end{array}\right]=\frac{1}{34}\left[\begin{array}{c} 13(1)+8\left(\frac{3}{2}\right)+1(9) \\ 5(1)+(-10)\left(\frac{3}{2}\right)+3(9) \\ 3(1)+(-6)\left(\frac{3}{2}\right)+(-5)(9) \end{array}\right] \end{aligned}$

$\begin{aligned} & \Rightarrow\left[\begin{array}{l} x \\ y \\ z \end{array}\right]=\frac{1}{34}\left[\begin{array}{c} 13+12+9 \\ 5-15+27 \\ 3-9-45 \end{array}\right] \\ & \Rightarrow\left[\begin{array}{l} x \\ y \\ z \end{array}\right]=\frac{1}{34}\left[\begin{array}{c} 34 \\ 17 \\ -51 \end{array}\right] \Rightarrow\left[\begin{array}{l} x \\ y \\ z \end{array}\right]=\left[\begin{array}{c} 1 \\ \frac{1}{2} \\ \frac{-3}{2} \end{array}\right] \end{aligned}$

Hence, $x=1, y=\frac{1}{2}$, and $z=-\frac{3}{2}$.

12. $x-y+z=4$

$\quad\quad$$2 x+y-3 z=0$

$\quad\quad$$x+y+z=2$

Solution

The given system of equations can be written in the form of $A X=B$, where

$A= \begin{bmatrix} 1 & -1 & 1 \\ 2 & 1 & -3 \\ 1 & 1 & 1\end{bmatrix} , X= \begin{bmatrix} x \\ y \\ z\end{bmatrix} $ and $B= \begin{bmatrix} 4 \\ 0 \\ 2 \end{bmatrix} $.

Now,

$|A|=1(1+3)+1(2+3)+1(2-1)=4+5+1=10 \neq 0$

Thus, $A$ is non-singular. Therefore, its inverse exists.

$ \begin{aligned} & \text{ Now, } A _{11}=4, A _{12}=-5, A _{13}=1 \\ & A _{21}=2, A _{22}=0, A _{23}=-2 \\ & A _{31}=2, A _{32}=5, A _{33}=3 \\ & \therefore A^{-1}=\frac{1}{|A|}(adj A)=\frac{1}{10} \begin{bmatrix} 4 & 2 & 2 \\ -5 & 0 & 5 \\ 1 & -2 & 3 \end{bmatrix} \\ & \therefore X=A^{-1} B=\frac{1}{10} \begin{bmatrix} 4 & 2 & 2 \\ -5 & 0 & 5 \\ 1 & -2 & 3 \end{bmatrix} \begin{bmatrix} 4 \\ 0 \\ 2 \end{bmatrix} \\ & \Rightarrow \begin{bmatrix} x \\ y \\ z \end{bmatrix} =\frac{1}{10} \begin{bmatrix} 16+0+4 \\ -20+0+10 \\ 4+0+6 \end{bmatrix} \\ & \quad=\frac{1}{10} \begin{bmatrix} 20 \\ -10 \\ 10 \end{bmatrix} \\ & \quad= \begin{bmatrix} 2 \\ -1 \\ 1 \end{bmatrix} \end{aligned} $

Hence, $x=2, y=-1$, and $z=1$.

13. $2 x+3 y+3 z=5$

$\quad\quad$$x-2 y+z=-4$

$\quad\quad$$3 x-y-2 z=3$

Solution

The given system of equations can be written in the form $A X=B$, where

$A= \begin{bmatrix} 2 & 3 & 3 \\ 1 & -2 & 1 \\ 3 & -1 & -2\end{bmatrix} , X= \begin{bmatrix} x \\ y \\ z\end{bmatrix} $ and $B= \begin{bmatrix} 5 \\ -4 \\ 3 \end{bmatrix} $.

Now,

$|A|=2(4+1)-3(-2-3)+3(-1+6)=2(5)-3(-5)+3(5)=10+15+15=40 \neq 0$

Thus, $A$ is non-singular. Therefore, its inverse exists.

Now, $A _{11}=5, A _{12}=5, A _{13}=5$

$A _{21}=3, A _{22}=-13, A _{23}=11$

$A _{31}=9, A _{32}=1, A _{33}=-7$

$\therefore A^{-1}=\frac{1}{|A|}(adj A)=\frac{1}{40} \begin{bmatrix} 5 & 3 & 9 \\ 5 & -13 & 1 \\ 5 & 11 & -7 \end{bmatrix} $

$\therefore X=A^{-1} B=\frac{1}{40} \begin{bmatrix} 5 & 3 & 9 \\ 5 & -13 & 1 \\ 5 & 11 & -7\end{bmatrix} \begin{bmatrix} 5 \\ -4 \\ 3 \end{bmatrix} $

$\Rightarrow \begin{bmatrix} x \\ y \\ z\end{bmatrix} =\frac{1}{40} \begin{bmatrix} 25-12+27 \\ 25+52+3 \\ 25-44-21 \end{bmatrix} $

$=\frac{1}{40} \begin{bmatrix} 40 \\ 80 \\ -40 \end{bmatrix} $

$= \begin{bmatrix} 1 \\ 2 \\ -1 \end{bmatrix} $

Hence, $x=1, y=2$, and $z=-1$.

14. $x-y+2 z=7$

$\quad\quad$$3 x+4 y-5 z=-5$

$\quad\quad$$2 x-y+3 z=12$

Solution

The given system of equations can be written in the form of $A X=B$, where

$ A= \begin{bmatrix} 1 & -1 & 2 \\ 3 & 4 & -5 \\ 2 & -1 & 3 \end{bmatrix} , X= \begin{bmatrix} x \\ y \\ z \end{bmatrix} \text{ and } B= \begin{bmatrix} 7 \\ -5 \\ 12 \end{bmatrix} \text{. } $

Now,

$|A|=1(12-5)+1(9+10)+2(-3-8)=7+19-22=4 \neq 0$

Thus, $A$ is non-singular. Therefore, its inverse exists.

$ \begin{aligned} & \text{ Now, } A _{11}=7, A _{12}=-19, A _{13}=-11 \\ & A _{21}=1, A _{22}=-1, A _{23}=-1 \\ & A _{31}=-3, A _{32}=11, A _{33}=7 \\ & \therefore A^{-1}=\frac{1}{|A|}(\text{ adj } A)=\frac{1}{4} \begin{bmatrix} 7 & 1 & -3 \\ -19 & -1 & 11 \\ -11 & -1 & 7 \end{bmatrix} \\ & \therefore X=A^{-1} B=\frac{1}{4} \begin{bmatrix} 7 & 1 & -3 \\ -19 & -1 & 11 \\ -11 & -1 & 7 \end{bmatrix} \begin{bmatrix} 7 \\ -5 \\ 12 \end{bmatrix} \\ & \Rightarrow \begin{bmatrix} x \\ y \\ z \end{bmatrix} =\frac{1}{4} \begin{bmatrix} 49-5-36 \\ -133+5+132 \\ -77+5+84 \end{bmatrix} \\ & \quad=\frac{1}{4} \begin{bmatrix} 8 \\ 4 \\ 12 \end{bmatrix} = \begin{bmatrix} 2 \\ 1 \\ 3 \end{bmatrix} \end{aligned} $

Hence, $x=2, y=1$, and $z=3$.

15. If $A=\begin{vmatrix}2 & -3 & 5 \\ 3 & 2 & -4 \\ 1 & 1 & -2\end{vmatrix}$, find $A^{-1}$. Using $A^{-1}$ solve the system of equations

$ \begin{aligned}\quad\quad 2 x-3 y+5 z & =11 \\ 3 x+2 y-4 z & =-5 \\ x+y-2 z & =-3 \end{aligned} $

Solution

$ \begin{aligned} & A= \begin{bmatrix} 2 & -3 & 5 \\ 3 & 2 & -4 \\ 1 & 1 & -2 \end{bmatrix} \\ & \therefore|A|=2(-4+4)+3(-6+4)+5(3-2)=0-6+5=-1 \neq 0 \end{aligned} $

Now, $A _{11}=0, A _{12}=2, A _{13}=1$

$A _{21}=-1, A _{22}=-9, A _{23}=-5$

$A _{31}=2, A _{32}=23, A _{33}=13$

$\therefore A^{-1}=\frac{1}{|A|}(adj A)=- \begin{bmatrix} 0 & -1 & 2 \\ 2 & -9 & 23 \\ 1 & -5 & 13\end{bmatrix} = \begin{bmatrix} 0 & 1 & -2 \\ -2 & 9 & -23 \\ -1 & 5 & -13 \end{bmatrix} $

Now, the given system of equations can be written in the form of $A X=B$, where

$ A= \begin{bmatrix} 2 & -3 & 5 \\ 3 & 2 & -4 \\ 1 & 1 & -2 \end{bmatrix} , X= \begin{bmatrix} x \\ y \\ z \end{bmatrix} \text{ and } B= \begin{bmatrix} 11 \\ -5 \\ -3 \end{bmatrix} \text{. } $

The solution of the system of equations is given by $X=A^{-1} B$.

$ \begin{aligned} & X=A^{-1} B \end{aligned} $

$\Rightarrow \begin{bmatrix}x \\ y \\ z \end{bmatrix}=\begin{bmatrix}0 & 1 & -2 \\ -2 & 9 & -23 \\ -1 & 5 & -13 \end{bmatrix} \begin{bmatrix}11 \\ -5 \\ -3 \end{bmatrix}$

$ \begin{aligned} & = \begin{bmatrix} 0-5+6 \\ -22-45+69 \\ -11-25+39 \end{bmatrix} \\ & = \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} \end{aligned} $

Hence, $x=1, y=2$, and $z=3$.

16. The cost of $4 kg$ onion, $3 kg$ wheat and $2 kg$ rice is ₹ 60 . The cost of $2 kg$ onion, $4 kg$ wheat and $6 kg$ rice is ₹ 90 . The cost of $6 kg$ onion $2 kg$ wheat and $3 kg$ rice is ₹ 70. Find cost of each item per $kg$ by matrix method.

Solution

Let the cost of onions, wheat, and rice per $kg$ be $Rs x, Rs y$, and $Rs z$ respectively.

Then, the given situation can be represented by a system of equations as:

$4 x+3 y+2 z=60$

$2 x+4 y+6 z=90$

$6 x+2 y+3 z=70$

This system of equations can be written in the form of $A X=B$, where

$ \begin{aligned} & A= \begin{bmatrix} 4 & 3 & 2 \\ 2 & 4 & 6 \\ 6 & 2 & 3 \end{bmatrix} , X= \begin{bmatrix} x \\ y \\ z \end{bmatrix} \text{ and } B= \begin{bmatrix} 60 \\ 90 \\ 70 \end{bmatrix} \text{. } \\ & |A|=4(12-12)-3(6-36)+2(4-24)=0+90 \\ & \text{ Now, } \quad \begin{matrix} A _{11}=0, A _{12}=30, A _{13}=-20 \\ A _{21}=-5, A _{22}=0, A _{23}=10 \\ A _{31}=10, A _{32}=-20, A _{33}=10 \end{matrix} \end{aligned} $

$ |A|=4(12-12)-3(6-36)+2(4-24)=0+90-40=50 \neq 0 $

$ \begin{aligned} & \therefore adj A= \begin{bmatrix} 0 & -5 & 10 \\ 30 & 0 & -20 \\ -20 & 10 & 10 \end{bmatrix} \\ & \therefore A^{-1}=\frac{1}{|A|} \text{ adj } A=\frac{1}{50} \begin{bmatrix} 0 & -5 & 10 \\ 30 & 0 & -20 \\ -20 & 10 & 10 \end{bmatrix} \end{aligned} $

Now,

$ \begin{aligned} & X=A^{-1} B \\ & \Rightarrow X=\frac{1}{50} \begin{bmatrix} 0 & -5 & 10 \\ 30 & 0 & -20 \\ -20 & 10 & 10 \end{bmatrix} \begin{bmatrix} 60 \\ 90 \\ 70 \end{bmatrix} \\ & \Rightarrow \begin{bmatrix} x \\ y \\ z \end{bmatrix} =\frac{1}{50} \begin{bmatrix} 0-450+700 \\ 1800+0-1400 \\ -1200+900+700 \end{bmatrix} \\ & =\frac{1}{50} \begin{bmatrix} 250 \\ 400 \\ 400 \end{bmatrix} \\ & = \begin{bmatrix} 5 \\ 8 \\ 8 \end{bmatrix} \\ & \therefore x=5, y=8 \text{ and } z=8 . \end{aligned} $

Hence, the cost of onions is Rs 5 per kg, the cost of wheat is Rs 8 per kg, and the cost of rice is Rs 8 per kg.

Example 19 Use product $\begin{vmatrix}1 & 1 & 2\\ 0 & 2 & 3 \\3 & 2 & 4 \end{vmatrix}$ $\begin{vmatrix}-2 & 0 & 1\\ 9 & 2 & 3 \\6 & 1 & 2 \end{vmatrix}$ to solve the system of equations

$ \begin{aligned} & x-y+2 z=1 \\ & 2 y-3 z=1 \\ & 3 x-2 y+4 z=2 \end{aligned} $

Solution Consider the product $\begin{vmatrix}1 & -1 & 2 \\ 0 & 2 & -3 \\ 3 & -2 & 4\end{vmatrix}\begin{vmatrix}-2 & 0 & 1 \\ 9 & 2 & -3 \\ 6 & 1 & -2\end{vmatrix}$

$ =\begin{vmatrix} -2-9+12 & 0-2+2 & 1+3-4 \\ 0+18-18 & 0+4-3 & 0-6+6 \\ -6-18+24 & 0-4+4 & 3+6-8 \end{vmatrix}=\begin{vmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{vmatrix} $

$ \begin{vmatrix} 1 & -1 & 2^{-1} & -2 & 0 & 1 \end{vmatrix} $

Hence

$ \begin{vmatrix}1 & 1 & 2\\ 0 & 2 & 3 \\3 & 2 & 4 \end{vmatrix} =\begin{vmatrix}-2 & 0 & 1\\ 9 & 2 & 3 \\6 & 1 & 2 \end{vmatrix} $

Now, given system of equations can be written, in matrix form, as follows

$ \begin{vmatrix} 1 & -1 & 2 \\ 0 & 2 & -3 \\ 3 & -2 & 4 \end{vmatrix}\begin{vmatrix}{l} x \\ y \\ z \end{vmatrix}=\begin{vmatrix}{l} 1 \\ 1 \\ 2 \end{vmatrix} $ or

Hence

$ \begin{aligned} & \begin{vmatrix} x \\ y \\ z \end{vmatrix}=\begin{vmatrix} 1 & -1 & 2 \\ 0 & 2 & -3 \\ 3 & -2 & 4 \end{vmatrix} ^{-1}\begin{vmatrix} 1 \\ 1 \\ 2 \end{vmatrix}=\begin{vmatrix} 2 & 0 & 1 \\ 9 & 2 & 3 \\ 6 & 1 & 2 \end{vmatrix}\begin{vmatrix} 1 \\ 1 \\ 2 \end{vmatrix} \\ & =\begin{vmatrix} -2+0+2 \\ 9+2-6 \\ 6+1-4 \end{vmatrix}=\begin{vmatrix} 0 \\ 5 \\ 3 \end{vmatrix} \end{aligned} $

$ x=0, y=5 \text{ and } z=3 $

Miscellaneous Exercises on Chapter 4

1. Prove that the determinant $\begin{vmatrix}x & \sin \theta & \cos \theta \\ -\sin \theta & -x & 1 \\ \cos \theta & 1 & x\end{vmatrix}$ is independent of $\theta$.

Solution

$ \begin{aligned} \Delta & = \begin{vmatrix} x & \sin \theta & \cos \theta \\ -\sin \theta & -x & 1 \\ \cos \theta & 1 & x \end{vmatrix} \\ & =x(x^{2}-1)-\sin \theta(-x \sin \theta-\cos \theta)+\cos \theta(-\sin \theta+x \cos \theta) \\ & =x^{3}-x+x \sin ^{2} \theta+\sin \theta \cos \theta-\sin \theta \cos \theta+x \cos ^{2} \theta \\ & =x^{3}-x+x(\sin ^{2} \theta+\cos ^{2} \theta) \\ & =x^{3}-x+x \\ & =x^{3} \text{ (Independent of } \theta \text{ ) } \end{aligned} $

Hence, $\Delta$ is independent of $\theta$.

2. Evaluate $\begin{vmatrix}\cos \alpha \cos \beta & \cos \alpha \sin \beta & -\sin \alpha \\ -\sin \beta & \cos \beta & 0 \\ \sin \alpha \cos \beta & \sin \alpha \sin \beta & \cos \alpha\end{vmatrix}$.

Solution

$ \Delta= \begin{vmatrix} \cos \alpha \cos \beta & \cos \alpha \sin \beta & -\sin \alpha \\ -\sin \beta & \cos \beta & 0 \\ \sin \alpha \cos \beta & \sin \alpha \sin \beta & \cos \alpha \end{vmatrix} $

Expanding along $C_3$, we have:

$ \begin{aligned} \Delta & =-\sin \alpha(-\sin \alpha \sin ^{2} \beta-\cos ^{2} \beta \sin \alpha)+\cos \alpha(\cos \alpha \cos ^{2} \beta+\cos \alpha \sin ^{2} \beta) \\ & =\sin ^{2} \alpha(\sin ^{2} \beta+\cos ^{2} \beta)+\cos ^{2} \alpha(\cos ^{2} \beta+\sin ^{2} \beta) \\ & =\sin ^{2} \alpha(1)+\cos ^{2} \alpha(1) \\ & =1 \end{aligned} $

3. If $A^{-1}=\begin{vmatrix}3 & -1 & 1 \\ -15 & 6 & -5 \\ 5 & -2 & 2\end{vmatrix}$ and $B=\begin{vmatrix}1 & 2 & -2 \\ -1 & 3 & 0 \\ 0 & -2 & 1\end{vmatrix}$, find $(A B)^{-1}$

Solution

Given: $A^{-1}=\begin{vmatrix}3 & -1 & 1 \\ -15 & 6 & -5 \\ 5 & -2 & 2\end{vmatrix}$ and $B=\begin{vmatrix}1 & 2 & -2 \\ -1 & 3 & 0 \\ 0 & -2 & 1\end{vmatrix}$

We know that $(A B)^{-1}=B^{-1} A^{-1}$

$\begin{aligned} & |B|=\begin{vmatrix} 1 & 2 & -2 \\ -1 & 3 & 0 \\ 0 & -2 & 1 \end{vmatrix} \\ & \Rightarrow|B|=1(3-0)-2(-1-0)-2(2-0) \\ & \Rightarrow|B|=1(3)-2(-1)-2(2) \\ & \Rightarrow|B|=3+2-4=1 \end{aligned}$

Since, $|B| \neq 0$

Thus,$B^{-1}$ exists.

$\begin{aligned} & B=\begin{vmatrix} 1 & 2 & -2 \\ -1 & 3 & 0 \\ 0 & -2 & 1 \end{vmatrix} \\ & M_{11}=\begin{vmatrix} 3 & 0 \\ -2 & 1 \end{vmatrix}=3(1)-(-2) 0=3 \\ & M_{12}=\begin{vmatrix} -1 & 0 \\ 0 & 1 \end{vmatrix}=1(1)-(0) 0=-1 \\ & M_{13}=\begin{vmatrix} -1 & 3 \\ 0 & -2 \end{vmatrix}=(-1)(-2)-O(3)=2 \\ & M_{21}=\begin{vmatrix} 2 & -2 \\ -2 & 1 \end{vmatrix}=2(1)-(-2)(-2)=-2 \end{aligned}$

$\begin{aligned} & M_{22}=\begin{vmatrix} 1 & -2 \\ 0 & 1 \end{vmatrix}=1(1) O(-2)=1 \\ & M_{23}=\begin{vmatrix} 1 & 2 \\ 0 & -2 \end{vmatrix}=1(-2)-0(2)=-2 \\ & M_{31}=\begin{vmatrix} 2 & -2 \\ 3 & 0 \end{vmatrix}=2(0)-3(-2)=6 \\ & M_{32}=\begin{vmatrix} 1 & -2 \\ -1 & 0 \end{vmatrix}=1(0)-(-1)(-2)=-2 \\ & M_{33}=\begin{vmatrix} 1 & 2 \\ -1 & 3 \end{vmatrix}=1(3)-(-1) 2=5 \end{aligned}$

$\begin{aligned} & \therefore \operatorname{adj}(B)=\begin{vmatrix} M_{11} & -M_{21} & M_{31} \\ -M_{12} & M_{22} & -M_{31} \\ M_{13} & -M_{23} & M_{33} \end{vmatrix} \\ & \begin{vmatrix} 3 & 2 & 6 \\ 1 & 1 & 2 \\ 2 & 2 & 5 \end{vmatrix} \end{aligned}$

Now,

$B^{-1}=\frac{1}{|B|} \operatorname{adj}(B)$

$\Rightarrow B^{-1}=\frac{1}{1}\begin{vmatrix} 3 & 2 & 6 \\ 1 & 1 & 2 \\ 2 & 2 & 5 \end{vmatrix}$

$\begin{aligned} &\Rightarrow B^{-1}=\begin{vmatrix} 3 & 2 & 6 \\ 1 & 1 & 2 \\ 2 & 2 & 5 \end{vmatrix}\\ &B^{-1} A^{-1}=\begin{vmatrix} 3 & 2 & 6 \\ 1 & 1 & 2 \\ 2 & 2 & 5 \end{vmatrix}\begin{vmatrix} 3 & -1 & 1 \\ -15 & 6 & -5 \\ 5 & -2 & 2 \end{vmatrix}\\ &\Rightarrow \mathrm{B}^{-1} \mathrm{~A}^{-1}\\ &=\begin{vmatrix} 9-30+30 & -3+12-12 & 3-10+12 \\ 3-15+10 & -1+6-4 & 1-5+4 \\ 6-30+25 & -2+12-10 & 2-10+10 \end{vmatrix}\\ &B^{-1} A^{-1}=\begin{vmatrix} 9 & -3 & 5 \\ -2 & 1 & 0 \\ 1 & 0 & 2 \\ \end{vmatrix} \end{aligned}$

So, $(A B)^{-1}=B^{-1} A^{-1}=\begin{vmatrix}9 & -3 & 5 \\ -2 & 1 & 0 \\ 1 & 0 & 2\end{vmatrix}$

Therefore, $(A B)^{-1}=\begin{vmatrix}9 & -3 & 5 \\ -2 & 1 & 0 \\ 1 & 0 & 2\end{vmatrix}$

4. Let $A= \begin{vmatrix} 1 & -2 & 1 \\ -2 & 3 & 1 \\ 1 & 1 & 5 \end{vmatrix} $ verify that

(i) $[adj A]^{-1}=adj(A^{-1})$

(ii) $(A^{-1})^{-1}=A$

Solution

$ \begin{aligned} & A= \begin{vmatrix} 1 & -2 & 1 \\ -2 & 3 & 1 \\ 1 & 1 & 5 \end{vmatrix} \\ & \therefore|A|=1(15-1)+2(-10-1)+1(-2-3)=14-22-5=-13 \end{aligned} $

$ \begin{aligned} & \text{ Now, } A _{11}=14, A _{12}=11, A _{13}=-5 \\ & A _{21}=11, A _{22}=4, A _{23}=-3 \\ & A _{31}=-5, A _{32}=-3, A _{13}=-1 \\ & \therefore \text{ adj } A= \begin{vmatrix} 14 & 11 & -5 \\ 11 & 4 & -3 \\ -5 & -3 & -1 \end{vmatrix} \\ & \therefore A^{-1}=\frac{1}{|A|}(\text{ adj } A) \\ & \quad=-\frac{1}{13} \begin{vmatrix} 14 & 11 & -5 \\ 11 & 4 & -3 \\ -5 & -3 & -1 \end{vmatrix} =\frac{1}{13} \begin{vmatrix} -14 & -11 & 5 \\ -11 & -4 & 3 \\ 5 & 3 & 1 \end{vmatrix} \end{aligned} $

(i)

$ \begin{aligned} \text{ adj } A & =14(-4-9)-11(-11-15)-5(-33+20) \\ & =14(-13)-11(-26)-5(-13) \\ & =-182+286+65=169 \end{aligned} $

We have,

$ \begin{aligned} & adj(adj A)= \begin{vmatrix} -13 & 26 & -13 \\ 26 & -39 & -13 \\ -13 & -13 & -65 \end{vmatrix} \\ & \therefore[adj A]^{-1}=\frac{1}{|adj A|}(adj(adj A)) \\ & =\frac{1}{169} \begin{vmatrix} -13 & 26 & -13 \\ 26 & -39 & -13 \\ -13 & -13 & -65 \end{vmatrix} \\ & =\frac{1}{13} \begin{vmatrix} -1 & 2 & -1 \\ 2 & -3 & -1 \\ -1 & -1 & -5 \end{vmatrix} \\ & \text{ Now, } A^{-1}=\frac{1}{13} \begin{vmatrix} -14 & -11 & 5 \\ -11 & -4 & 3 \\ 5 & 3 & 1 \end{vmatrix} = \begin{vmatrix} -\frac{14}{13} & -\frac{11}{13} & \frac{5}{13} \\ -\frac{11}{13} & -\frac{4}{13} & \frac{3}{13} \\ \frac{5}{13} & \frac{3}{13} & \frac{1}{13} \end{vmatrix} \\ & \therefore adj(A^{-1})= \begin{vmatrix} -\frac{4}{169}-\frac{9}{169} & -(-\frac{11}{169}-\frac{15}{169}) & -\frac{33}{169}+\frac{20}{169} \\ -(-\frac{11}{169}-\frac{15}{169}) & -\frac{14}{169}-\frac{25}{169} & -(-\frac{42}{169}+\frac{55}{169}) \\ -\frac{33}{169}+\frac{20}{169} & -(-\frac{42}{169}+\frac{55}{169}) & \frac{56}{169}-\frac{121}{169} \end{vmatrix} \\ & =\frac{1}{169} \begin{vmatrix} -13 & 26 & -13 \\ 26 & -39 & -13 \\ -13 & -13 & -65 \end{vmatrix} =\frac{1}{13} \begin{vmatrix} -1 & 2 & -1 \\ 2 & -3 & -1 \\ -1 & -1 & -5 \end{vmatrix} \end{aligned} $

Hence, $[adj A]^{-1}=adj(A^{-1})$.

(ii)

We have shown that:

$A^{-1}=\frac{1}{13} \begin{vmatrix} -14 & -11 & 5 \\ -11 & -4 & 3 \\ 5 & 3 & 1 \end{vmatrix} $

And, $adj A^{-1}=\frac{1}{13} \begin{vmatrix} -1 & 2 & -1 \\ 2 & -3 & -1 \\ -1 & -1 & -5 \end{vmatrix} $

Now,

$|A^{-1}|=(\frac{1}{13})^{3}[-14 \times(-13)+11 \times(-26)+5 \times(-13)]=(\frac{1}{13})^{3} \times(-169)=-\frac{1}{13}$

$\therefore(A^{-1})^{-1}=\frac{\text{ adj } A^{-1}}{|A^{-1}|}=\frac{1}{(-\frac{1}{13})} \times \frac{1}{13} \begin{vmatrix} -1 & 2 & -1 \\ 2 & -3 & -1 \\ -1 & -1 & -5\end{vmatrix} = \begin{vmatrix} 1 & -2 & 1 \\ -2 & 3 & 1 \\ 1 & 1 & 5 \end{vmatrix} =A$

$\therefore(A^{-1})^{-1}=A$

5. Evaluate $\begin{vmatrix}x & y & x+y \\ y & x+y & x \\ x+y & x & y\end{vmatrix}$

Solution

$\Delta= \begin{vmatrix} x & y & x+y \\ y & x+y & x \\ x+y & x & y\end{vmatrix} $

Applying $R_1 \to R_1+R_2+R_3$, we have:

$\Delta= \begin{vmatrix} 2(x+y) & 2(x+y) & 2(x+y) \\ y & x+y & x \\ x+y & x & y\end{vmatrix} $

$=2(x+y) \begin{vmatrix} 1 & 1 & 1 \\ y & x+y & x \\ x+y & x & y\end{vmatrix} $

Applying $C_2 \to C_2-C_1$ and $C_3 \to C_3-C_1$, we have:

$\Delta=2(x+y) \begin{vmatrix} 1 & 0 & 0 \\ y & x & x-y \\ x+y & -y & -x\end{vmatrix} $

Expanding along $R_1$, we have:

$ \begin{aligned} \Delta & =2(x+y)[-x^{2}+y(x-y)] \\ & =-2(x+y)(x^{2}+y^{2}-y x) \\ & =-2(x^{3}+y^{3}) \end{aligned} $

6. Evaluate $\begin{vmatrix}1 & x & y \\ 1 & x+y & y \\ 1 & x & x+y\end{vmatrix}$

Solution

Applying $R_2 \to R_2-R_1$ and $R_3 \to R_3-R_1$, we have:

$\Delta= \begin{vmatrix} 1 & x & y \\ 0 & y & 0 \\ 0 & 0 & x\end{vmatrix} $

Expanding along $C_1$, we have:

$\Delta=1(x y-0)=x y$

Using properties of determinants in Exercises 11 to 15, prove that:

7. Solve the system of equations

$ \begin{aligned} & \frac{2}{x}+\frac{3}{y}+\frac{10}{z}=4 \\ & \frac{4}{x}-\frac{6}{y}+\frac{5}{z}=1 \\ & \frac{6}{x}+\frac{9}{y}-\frac{20}{z}=2 \end{aligned} $

Solution

Let $\frac{1}{x}=p, \frac{1}{y}=q, \frac{1}{z}=r$.

Then the given system of equations is as follows:

$2 p+3 q+10 r=4$

$4 p-6 q+5 r=1$

$6 p+9 q-20 r=2$

This system can be written in the form of $A X=B$, where

$A= \begin{bmatrix} 2 & 3 & 10 \\ 4 & -6 & 5 \\ 6 & 9 & -20\end{bmatrix} , X= \begin{bmatrix} p \\ q \\ r\end{bmatrix} $ and $B= \begin{bmatrix} 4 \\ 1 \\ 2 \end{bmatrix} $.

Now,

$ \begin{aligned} |A| & =2(120-45)-3(-80-30)+10(36+36) \\ & =150+330+720 \\ & =1200 \end{aligned} $

Thus, $A$ is non-singular. Therefore, its inverse exists.

Now,

$A _{11}=75, A _{12}=110, A _{13}=72$

$A _{21}=150, A _{22}=-100, A _{23}=0$

$A _{31}=75, A _{32}=30, A _{33}=-24$

$\therefore A^{-1}=\frac{1}{|A|}$ adj $A$

$ =\frac{1}{1200} \begin{bmatrix} 75 & 150 & 75 \\ 110 & -100 & 30 \\ 72 & 0 & -24 \end{bmatrix} $

Now,

$ \begin{aligned} & X=A^{-1} B \\ & \begin{aligned} \Rightarrow \begin{bmatrix} p \\ q \\ r \end{bmatrix} & =\frac{1}{1200} \begin{bmatrix} 75 & 150 & 75 \\ 110 & -100 & 30 \\ 72 & 0 & -24 \end{bmatrix} \begin{bmatrix} 4 \\ 1 \\ 2 \end{bmatrix} \\ & =\frac{1}{1200} \begin{bmatrix} 300+150+150 \\ 440-100+60 \\ 288+0-48 \end{bmatrix} \\ & =\frac{1}{1200} \begin{bmatrix} 600 \\ 400 \\ 240 \end{bmatrix} = \begin{bmatrix} \frac{1}{2} \\ \frac{1}{3} \\ \frac{1}{5} \end{bmatrix} \end{aligned} \\ & \therefore p=\frac{1}{2}, q=\frac{1}{3} \text{, and } r=\frac{1}{5} \end{aligned} $

Hence, $x=2, y=3$, and $z=5$.

Choose the correct answer in Exercise 17 to 19.

8. If $x, y, z$ are nonzero real numbers, then the inverse of matrix $A=\begin{vmatrix}x & 0 & 0 \\ 0 & y & 0 \\ 0 & 0 & z\end{vmatrix}$ is

(A) $\begin{vmatrix}x^{-1} & 0 & 0 \\ 0 & y^{-1} & 0 \\ 0 & 0 & z^{-1}\end{vmatrix}$

(B) $x y z\begin{vmatrix}x^{-1} & 0 & 0 \\ 0 & y^{-1} & 0 \\ 0 & 0 & z^{-1}\end{vmatrix}$

(C) $\frac{1}{x y z}\begin{vmatrix}x & 0 & 0 \\ 0 & y & 0 \\ 0 & 0 & z\end{vmatrix}$

(D) $\frac{1}{x y z}\begin{vmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{vmatrix}$

Solution

$A= \begin{vmatrix} x & 0 & 0 \\ 0 & y & 0 \\ 0 & 0 & z \end{vmatrix} $

$\therefore|A|=x(y z-0)=x y z \neq 0$

Now, $A _{11}=y z, A _{12}=0, A _{13}=0$

$A _{21}=0, A _{22}=x z, A _{23}=0$

$A _{31}=0, A _{32}=0, A _{33}=x y$

$\therefore adj A= \begin{vmatrix} y z & 0 & 0 \\ 0 & x z & 0 \\ 0 & 0 & x y \end{vmatrix} $

$\therefore A^{-1}=\frac{1}{|A|}$ adj $A$

$ \begin{aligned} &=\frac{1}{x y z} \begin{vmatrix} y z & 0 & 0 \\ 0 & x z & 0 \\ 0 & 0 & x y \end{vmatrix} \\ &= \begin{vmatrix} \frac{y z}{x y z} & 0 & 0 \\ 0 & \frac{x z}{x y z} & 0 \\ 0 & 0 & \frac{x y}{x y z} \end{vmatrix} \\ &= \begin{vmatrix} \frac{1}{x} & 0 & 0 \\ 0 & \frac{1}{y} & 0 \\ 0 & 0 & \frac{1}{z} \end{vmatrix} = \begin{vmatrix} x^{-1} & 0 & 0 \\ 0 & y^{-1} & 0 \\ 0 & 0 & z^{-1} \end{vmatrix} \end{aligned} $

The correct answer is A.

9. Let $A=\begin{vmatrix}1 & \sin \theta & 1 \\ -\sin \theta & 1 & \sin \theta \\ -1 & -\sin \theta & 1\end{vmatrix}$, where $0 \leq \theta \leq 2 \pi$. Then

(A) $Det(A)=0$

(B) $Det(A) \in(2, \infty)$

(C) $Det(A) \in(2,4)$

(D) $Det(A) \in[2,4]$

Solution

$ \begin{aligned} & A= \begin{vmatrix} 1 & \sin \theta & 1 \\ -\sin \theta & 1 & \sin \theta \\ -1 & -\sin \theta & 1 \end{vmatrix} \\ & \therefore|A|=1(1+\sin ^{2} \theta)-\sin \theta(-\sin \theta+\sin \theta)+1(\sin ^{2} \theta+1) \\ & \quad=1+\sin ^{2} \theta+\sin ^{2} \theta+1 \\ & \quad=2+2 \sin ^{2} \theta \\ & \quad=2(1+\sin ^{2} \theta) \end{aligned} $

Now, $0 \leq \theta \leq 2 \pi$

$\Rightarrow 0 \leq \sin \theta \leq 1$

$\Rightarrow 0 \leq \sin ^{2} \theta \leq 1$

$\Rightarrow 1 \leq 1+\sin ^{2} \theta \leq 2$

$\Rightarrow 2 \leq 2(1+\sin ^{2} \theta) \leq 4$

$\therefore Det(A) \in[2,4]$

The correct answer is D.

Summary

$\Delta $ Determinant of a matrix $A=[a _{11}] _{1 \times 1}$ is given by $|a _{11}|=a _{11}$

$\Delta $ Determinant of a matrix $A=\begin{vmatrix}a _{11} & a _{12} \\ a _{21} & a _{22}\end{vmatrix}$ is given by

$ |A|=\begin{vmatrix} a _{11} & a _{12} \\ a _{21} & a _{22} \end{vmatrix}=a _{11} a _{22}-a _{12} a _{21} $

$ a_1 \quad b_1 \quad c_1 $

$\Delta $ Determinant of a matrix $A=a_2 \quad b_2 \quad c_2$ is given by (expanding along $R_1$ )

$ \begin{vmatrix} a_3 & b_3 & c_3 \end{vmatrix} $

$ |A|=\begin{vmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{vmatrix}=a_1\begin{vmatrix} b_2 & c_2 \\ b_3 & c_3 \end{vmatrix}-b_1\begin{vmatrix} a_2 & c_2 \\ a_3 & c_3 \end{vmatrix}+c_1\begin{vmatrix} a_2 & b_2 \\ a_3 & b_3 \end{vmatrix} $

For any square matrix $\mathbf{A}$, the $|\mathbf{A}|$ satisfy following properties.

Area of a triangle with vertices $(x_1, y_1),(x_2, y_2)$ and $(x_3, y_3)$ is given by

$ \Delta=\frac{1}{2}\begin{vmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{vmatrix} $

• Minor of an element $a _{i j}$ of the determinant of matrix A is the determinant obtained by deleting $i^{i^{h}}$ row and $j^{\text{th }}$ column and denoted by $M _{i j}$.

Cofactor of $a _{i j}$ of given by $A _{i j}=(-1)^{i+j} M _{i j}$

• Value of determinant of a matrix A is obtained by sum of product of elements of a row (or a column) with corresponding cofactors. For example,

$ |A|=a _{11} A _{11}+a _{12} A _{12}+a _{13} A _{13} . $

• If elements of one row (or column) are multiplied with cofactors of elements of any other row (or column), then their sum is zero. For example, $a _{11} A _{21}+a _{12}$ $A _{22}+a _{13} A _{23}=0$

If $A=\begin{vmatrix}a _{11} & a _{12} & a _{13} \\ a _{21} & a _{22} & a _{23} \\ a _{31} & a _{32} & a _{33}\end{vmatrix}$, then $adj A=\begin{vmatrix}A _{11} & A _{21} & A _{31} \\ A _{12} & A _{22} & A _{32} \\ A _{13} & A _{23} & A _{33}\end{vmatrix}$, where $A _{i j}$ is cofactor of $a _{i j}$

• $A(adj A)=(adj A) A=|A| I$, where $A$ is square matrix of order $n$.
• A square matrix A is said to be singular or non-singular according as $|A|=0$ or $|A| \neq 0$.
• If $AB=BA=I$, where $B$ is square matrix, then $B$ is called inverse of $A$. Also $A^{-1}=B$ or $B^{-1}=A$ and hence $(A^{-1})^{-1}=A$.
• A square matrix $A$ has inverse if and only if $A$ is non-singular.

$A^{-1}=\frac{1}{|A|}(adj A)$

$\checkmark$ If $a_1 x+b_1 y+c_1 z=d_1$

$ \begin{aligned} & a_2 x+b_2 y+c_2 z=d_2 \\ & a_3 x+b_3 y+c_3 z=d_3, \end{aligned} $

then these equations can be written as $AX=B$, where

$ A=\begin{vmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{vmatrix}, X=\begin{vmatrix}{l} x \\ y \\ z \end{vmatrix} \text{ and } B=\begin{vmatrix}{l} d_1 \\ d_2 \\ d_3 \end{vmatrix} $

• Unique solution of equation $A X=B$ is given by $X=A^{-1} B$, where $|A| \neq 0$.
• A system of equation is consistent or inconsistent according as its solution exists or not.
• For a square matrix $A$ in matrix equation $AX=B$

(i) $|A| \neq 0$, there exists unique solution

(ii) $|A|=0$ and $(adj A) B \neq 0$, then there exists no solution

(iii) $|A|=0$ and $(adj A) B=0$, then system may or may not be consistent.

Historical Note

The Chinese method of representing the coefficients of the unknowns of several linear equations by using rods on a calculating board naturally led to the discovery of simple method of elimination. The arrangement of rods was precisely that of the numbers in a determinant. The Chinese, therefore, early developed the idea of subtracting columns and rows as in simplification of a determinant Mikami, China, pp 30, 93.

Seki Kowa, the greatest of the Japanese Mathematicians of seventeenth century in his work ‘Kai Fukudai no Ho’ in 1683 showed that he had the idea of determinants and of their expansion. But he used this device only in eliminating a quantity from two equations and not directly in the solution of a set of simultaneous linear equations. T. Hayashi, “The Fakudoi and Determinants in Japanese Mathematics,” in the proc. of the Tokyo Math. Soc., V.

Vendermonde was the first to recognise determinants as independent functions. He may be called the formal founder. Laplace (1772), gave general method of expanding a determinant in terms of its complementary minors. In 1773 Lagrange treated determinants of the second and third orders and used them for purpose other than the solution of equations. In 1801, Gauss used determinants in his theory of numbers.

The next great contributor was Jacques - Philippe - Marie Binet, (1812) who stated the theorem relating to the product of two matrices of $m$-columns and $n$ rows, which for the special case of $m=n$ reduces to the multiplication theorem.

Also on the same day, Cauchy (1812) presented one on the same subject. He used the word ‘determinant’ in its present sense. He gave the proof of multiplication theorem more satisfactory than Binet’s.

The greatest contributor to the theory was Carl Gustav Jacob Jacobi, after this the word determinant received its final acceptance.