MATRICES

The essence of Mathematics lies in its freedom. - CANTOR

Introduction

The knowledge of matrices is necessary in various branches of mathematics. Matrices are one of the most powerful tools in mathematics. This mathematical tool simplifies our work to a great extent when compared with other straight forward methods. The evolution of concept of matrices is the result of an attempt to obtain compact and simple methods of solving system of linear equations. Matrices are not only used as a representation of the coefficients in system of linear equations, but utility of matrices far exceeds that use. Matrix notation and operations are used in electronic spreadsheet programs for personal computer, which in turn is used in different areas of business and science like budgeting, sales projection, cost estimation, analysing the results of an experiment etc. Also, many physical operations such as magnification, rotation and reflection through a plane can be represented mathematically by matrices. Matrices are also used in cryptography. This mathematical tool is not only used in certain branches of sciences, but also in genetics, economics, sociology, modern psychology and industrial management.

In this chapter, we shall find it interesting to become acquainted with the fundamentals of matrix and matrix algebra.

3.1 Matrix

Suppose we wish to express the information that Radha has 15 notebooks. We may express it as [15] with the understanding that the number inside [ ] is the number of notebooks that Radha has. Now, if we have to express that Radha has 15 notebooks and 6 pens. We may express it as $\begin{bmatrix}15 & 6\end{bmatrix}$ with the understanding that first number inside [ ] is the number of notebooks while the other one is the number of pens possessed by Radha. Let us now suppose that we wish to express the information of possession of notebooks and pens by Radha and her two friends Fauzia and Simran which is as follows:

$$ \begin{array}{llllll} \text { Radha } & \text { has } & 15 & \text { notebooks } & \text { and } & 6 \text { pens, } \\ \text { Fauzia } & \text { has } & 10 & \text { notebooks } & \text { and } & 2 \text { pens, } \\ \text { Simran } & \text { has } & 13 & \text { notebooks } & \text { and } & 5 \text { pens. } \end{array} $$

Now this could be arranged in the tabular form as follows: $$ \begin{array}{lcc} & \text { Notebooks } & \text { Pens } \\ \text { Radha } & 15 & 6 \\ \text { Fauzia } & 10 & 2 \\ \text { Simran } & 13 & 5 \end{array} $$ and this can be expressed as

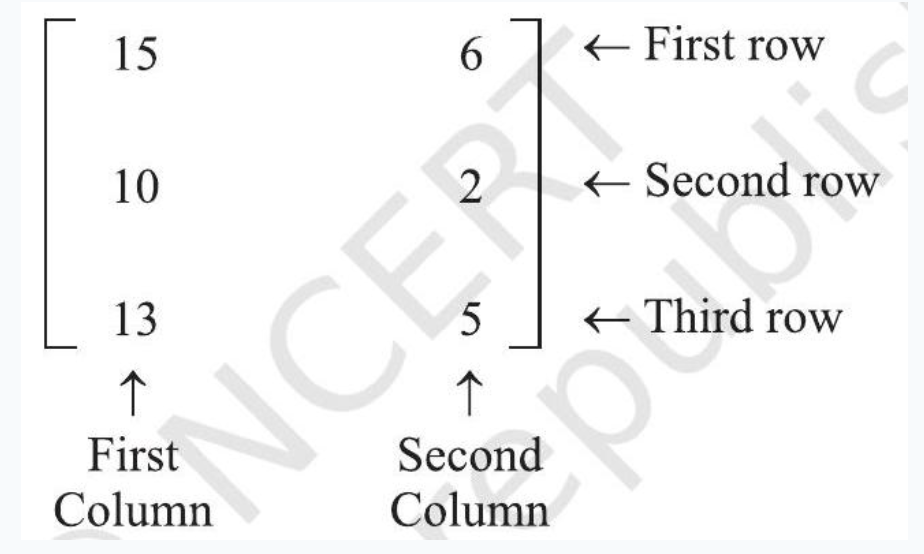
or

	Radha	Fauzia	Simran
Notebooks	15	10	13
Pens	6	2	5

which can be expressed as:

15	10	13
6	2	5

In the first arrangement the entries in the first column represent the number of note books possessed by Radha, Fauzia and Simran, respectively and the entries in the second column represent the number of pens possessed by Radha, Fauzia and Simran, respectively. Similarly, in the second arrangement, the entries in the first row represent the number of notebooks possessed by Radha, Fauzia and Simran, respectively. The entries in the second row represent the number of pens possessed by Radha, Fauzia and Simran, respectively. An arrangement or display of the above kind is called a matrix. Formally, we define matrix as:

Definition 1 A matrix is an ordered rectangular bmatrix of numbers or functions. The numbers or functions are called the elements or the entries of the matrix.

We denote matrices by capital letters. The following are some examples of matrices:

$$ A=\begin{bmatrix} -2 & 5 \\ 0 & \sqrt{5} \\ 3 & 6 \end{bmatrix}, B=\begin{bmatrix} 2+i & 3 & -\frac{1}{2} \\ 3.5 & -1 & 2 \\ \sqrt{3} & 5 & \frac{5}{7} \end{bmatrix}, C=\begin{bmatrix} 1+x & x^{3} & 3 \\ \cos x & \sin x+2 & \tan x \end{bmatrix} $$

In the above examples, the horizontal lines of elements are said to constitute, rows of the matrix and the vertical lines of elements are said to constitute, columns of the matrix. Thus $A$ has 3 rows and 2 columns, $B$ has 3 rows and 3 columns while $C$ has 2 rows and 3 columns.

3.1.1 Order of a matrix

A matrix having $m$ rows and $n$ columns is called a matrix of order $m \times n$ or simply $m \times n$ matrix (read as an $m$ by $n$ matrix). So referring to the above examples of matrices, we have $A$ as $3 \times 2$ matrix, $B$ as $3 \times 3$ matrix and $C$ as $2 \times 3$ matrix. We observe that $A$ has $3 \times 2=6$ elements, $B$ and $C$ have 9 and 6 elements, respectively.

In general, an $m \times n$ matrix has the following rectangular bmatrix:

$ \begin{bmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1j} & \cdots & a_{1n} \\ a_{21} & a_{22} & a_{23} & \cdots & a_{2j} & \cdots & a_{2n} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ a_{i1} & a_{i2} & a_{i3} & \cdots & a_{ij} & \cdots & a_{in} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ a_{m1} & a_{m2} & a_{m3} & \cdots & a_{mj} & \cdots & a_{mn} \end{bmatrix} _{m \times n} $

or $ A=[a_{i j}]_{m \times n}, 1 \leq i \leq m, 1 \leq j \leq n \quad i, j \in N $

Thus the $i^{\text {th }}$ row consists of the elements $a_{i 1}, a_{i 2}, a_{i 3}, \ldots, a_{i n}$, while the $j^{\text {th }}$ column consists of the elements $a_{1 j}, a_{2 j}, a_{3 j}, \ldots, a_{m j}$,

In general $a_{i j}$, is an element lying in the $i^{\text {th }}$ row and $j^{\text {th }}$ column. We can also call it as the $(i, j)^{\text {th }}$ element of $A$. The number of elements in an $m \times n$ matrix will be equal to $m n$.

Note In this chapter

1. We shall follow the notation, namely $A=[a_{i j}]_{m \times n}$ to indicate that $A$ is a matrix of order $m \times n$.

2. We shall consider only those matrices whose elements are real numbers or functions taking real values.

We can also represent any point $(x, y)$ in a plane by a matrix (column or row) as $\begin{bmatrix}x \\ y\end{bmatrix}$ (or $.[x, y]$). For example point $P(0,1)$ as a matrix representation may be given as

$$ \mathbf{P}=\begin{bmatrix} 0 \\ 1 \end{bmatrix} \text { or }\begin{bmatrix} 0 & 1 \end{bmatrix} $$

Observe that in this way we can also express the vertices of a closed rectilinear figure in the form of a matrix. For example, consider a quadrilateral $A B C D$ with vertices A $(1,0), B(3,2), C(1,3), D(-1,2)$.

Now, quadrilateral $ABCD$ in the matrix form, can be represented as

Thus, matrices can be used as representation of vertices of geometrical figures in a plane.

Now, let us consider some examples.

Example 1 Consider the following information regarding the number of men and women workers in three factories I, II and III

	Men workers	Women workers
I	30	25
II	25	31
III	27	26

Represent the above information in the form of a $3 \times 2$ matrix. What does the entry in the third row and second column represent?

Solution The information is represented in the form of a $3 \times 2$ matrix as follows:

$ A=\begin{bmatrix} 30 & 25 \\ 25 & 31 \\ 27 & 26 \end{bmatrix} $

The entry in the third row and second column represents the number of women workers in factory III.

Example 2 If a matrix has 8 elements, what are the possible orders it can have?

Solution We know that if a matrix is of order $m \times n$, it has $m n$ elements. Thus, to find all possible orders of a matrix with 8 elements, we will find all ordered pairs of natural numbers, whose product is 8 .

Thus, all possible ordered pairs are $(1,8),(8,1),(4,2),(2,4)$

Hence, possible orders are $1 \times 8,8 \times 1,4 \times 2,2 \times 4$

Example 3 Construct a $3 \times 2$ matrix whose elements are given by $a_{i j}=\frac{1}{2}|i-3 j|$.

Solution In general a $3 \times 2$ matrix is given by $A=\begin{bmatrix}a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32}\end{bmatrix}$.

Now $\quad$ $a_{i j}=\frac{1}{2}|i-3 j|, i=1,2,3 \text { and } j=1,2 $

Therefore $\quad a_{11}=\frac{1}{2}|1-3 \times 1|=1 \quad a_{12}=\frac{1}{2}|1-3 \times 2|=\frac{5}{2}$

$ \begin{matrix} a_{21}= \frac{1}{2}|2-3 \times 1|=\frac{1}{2} & a_{22}=\frac{1}{2}|2-3 \times 2|=2 \\ \\ a_{31} =\frac{1}{2}|3-3 \times 1|=0 & a_{32} =\frac{1}{2}|3-3 \times 2|=\frac{3}{2} \end{matrix} $

Hence the required matrix is given by $A=\begin{bmatrix}1 & \frac{5}{2} \\ \frac{1}{2} & 2 \\ 0 & \frac{3}{2}\end{bmatrix}$.

3.2 Types of Matrices

In this section, we shall discuss different types of matrices.

(i) Column matrix

A matrix is said to be a column matrix if it has only one column.

For example, $A=\begin{bmatrix}{c}0 \\ \sqrt{3} \\ -1 \\ 1 / 2\end{bmatrix}$ is a column matrix of order $4 \times 1$.

In general, $A=[a_{i j}]_{m \times 1}$ is a column matrix of order $m \times 1$.

(ii) Row matrix

A matrix is said to be a row matrix if it has only one row.

For example, $B=[\begin{bmatrix}-\frac{1}{2} & \sqrt{5} & 2 & 3\end{bmatrix}]_{1 \times 4}$ is a row matrix.

In general, $B=[b_{i j}]_{1 \times n}$ is a row matrix of order $1 \times n$.

(iii) Square matrix

A matrix in which the number of rows are equal to the number of columns, is said to be a square matrix. Thus an $m \times n$ matrix is said to be a square matrix if $m=n$ and is known as a square matrix of order ’ $n$ ‘.

For example $A=\begin{bmatrix}3 & -1 & 0 \\ \frac{3}{2} & 3 \sqrt{2} & 1 \\ 4 & 3 & -1\end{bmatrix}$ is a square matrix of order 3.

In general, $A=[a_{i j}]_{m \times m}$ is a square matrix of order $m$.

Note If $A=[a_{i j}]$ is a square matrix of order $n$, then elements (entries) $a_{11}, a_{22}, \ldots, a_{n n}$ are said to constitute the diagonal, of the matrix A. Thus, if $A=\begin{bmatrix}1 & -3 & 1 \\ 2 & 4 & -1 \\ 3 & 5 & 6\end{bmatrix}$.

Then the elements of the diagonal of A are 1, 4, 6 .

(iv) Diagonal matrix

A square matrix $B=[b_{ij}]_ {m\times m} $ is said to be a diagonal matrix if all its non diagonal elements are zero, that is a matrix $B=[b_{ij}]_ {m\times m} $ is said to be a diagonal matrix if $b_{i j}=0$, when $i \neq j$.

For example, $A=[4], B=\begin{bmatrix}-1 & 0 \\ 0 & 2\end{bmatrix}, C=\begin{bmatrix}-1.1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3\end{bmatrix}$, are diagonal matrices of order 1,2,3, respectively.

(v) Scalar matrix

A diagonal matrix is said to be a scalar matrix if its diagonal elements are equal, that is, a square matrix $B=[b_{i j}]_{n \times n}$ is said to be a scalar matrix if

$$ \begin{aligned} & b_{i j}=0, \quad \text { when } i \neq j \\ & b_{i j}=k, \quad \text { when } i=j, \text { for some constant } k . \end{aligned} $$

For example

$A=[3], \quad B=[\begin{bmatrix}-1 & 0 \\ 0 & -1\end{bmatrix}], \quad C=\begin{bmatrix}\sqrt{3} & 0 & 0 \\ 0 & \sqrt{3} & 0 \\ 0 & 0 & \sqrt{3}\end{bmatrix}$

are scalar matrices of order 1,2 and 3, respectively.

(vi) Identity matrix

A square matrix in which elements in the diagonal are all 1 and rest are all zero is called an identity matrix. In other words, the square matrix $A=[a_{i j}]_{n \times n}$ is an

identity matrix, if $a_{ij}=\begin{cases}1 & \text { if } & i=j \\ 0 & \text { if } & i \neq j\end{cases}.$.

We denote the identity matrix of order $n$ by $I_{n}$. When order is clear from the context, we simply write it as I.

For example [1], $\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix}$ $\begin{bmatrix}\sqrt 3 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & \sqrt 3\end{bmatrix}$ are identity matrices of order 1, 2 and 3, respectively.

Observe that a scalar matrix is an identity matrix when $k=1$. But every identity matrix is clearly a scalar matrix.

(vii) Zero matrix

A matrix is said to be zero matrix or null matrix if all its elements are zero.

For example, $[0],\begin{bmatrix}0 & 0 \\ 0 & 0\end{bmatrix},\begin{bmatrix}0 & 0 & 0 \\ 0 & 0 & 0\end{bmatrix},[0,0]$ are all zero matrices. We denote zero matrix by $O$. Its order will be clear from the context.

3.2.1 _Equality of matrices

Definition 2 Two matrices $A=[a_{i j}]$ and $B=[b_{i j}]$ are said to be equal if

(i) they are of the same order

(ii) each element of $A$ is equal to the corresponding element of $B$, that is $a_{i j}=b_{i j}$ for all $i$ and $j$.

For example, $\begin{bmatrix}2 & 3 \\ 0 & 1\end{bmatrix}$ and $\begin{bmatrix}2 & 3 \\ 0 & 1\end{bmatrix}$ are equal matrices but $\begin{bmatrix}3 & 2 \\ 0 & 1\end{bmatrix}$ and $\begin{bmatrix}2 & 3 \\ 0 & 1\end{bmatrix}$ are not equal matrices. Symbolically, if two matrices $A$ and $B$ are equal, we write $A=B$.

$$ \text { If }\begin{bmatrix} x & y \\ z & a \\ b & c \end{bmatrix}=\begin{bmatrix} -1.5 & 0 \\ 2 & \sqrt{6} \\ 3 & 2 \end{bmatrix} \text {, then } x=-1.5, y=0, z=2, a=\sqrt{6}, b=3, c=2 $$

Example 4 If $\begin{bmatrix}x+3 & z+4 & 2 y-7 \\ -6 & a-1 & 0 \\ b-3 & -21 & 0\end{bmatrix}=\begin{bmatrix}0 & 6 & 3 y-2 \\ -6 & -3 & 2 c+2 \\ 2 b+4 & -21 & 0\end{bmatrix}$

Find the values of $a, b, c, x, y$ and $z$.

Solution As the given matrices are equal, therefore, their corresponding elements must be equal. Comparing the corresponding elements, we get

$$ \begin{aligned} & x+3=0, \\ & z+4=6 \\ & 2 y-7=3 y-2 \\ & a-1=-3, \\ & 0=2 c+2 \\ & b-3=2 b+4 \text {, } \end{aligned} $$

Simplifying, we get

$$ a=-2, b=-7, c=-1, x=-3, y=-5, z=2 $$

Example 5 Find the values of $a, b, c$, and $d$ from the following equation:

$$ \begin{bmatrix} 2 a+b & a-2 b \\ 5 c-d & 4 c+3 d \end{bmatrix}=\begin{bmatrix} 4 & -3 \\ 11 & 24 \end{bmatrix} $$

Solution By equality of two matrices, equating the corresponding elements, we get

$$ \begin{bmatrix} 2 a+b & =4 & 5 c-d & =11 \\ a-2 b & =-3 & 4 c+3 d & =24 \end{bmatrix} $$

Solving these equations, we get

$$ a=1, b=2, c=3 \text { and } d=4 $$

EXERCISE 3.1

1. In the matrix $A=\begin{bmatrix}2 & 5 & 19 & -7 \\ 35 & -2 & \frac{5}{2} & 12 \\ \sqrt{3} & 1 & -5 & 17\end{bmatrix}$, write:

(i) The order of the matrix, (ii) The number of elements,

(iii) Write the elements $a_{13}, a_{21}, a_{33}, a_{24}, a_{23}$.

Solution

(i) In the given matrix, the number of rows is 3 and the number of columns is 4 .

Therefore, the order of the matrix is $3 \times 4$.

(ii) Since the order of the matrix is $3 \times 4$, there are $3 \times 4=12$ elements in it.

(iii) $a _{13}=19, a _{21}=35, a _{33}=-5, a _{24}=12, a _{23}=\frac{5}{2}$

2. If a matrix has 24 elements, what are the possible orders it can have? What, if it has 13 elements?

Solution

We know that if a matrix is of the order $m \times n$, it has $m n$ elements. Thus, to find all the possible orders of a matrix having 24 elements, we have to find all the ordered pairs of natural numbers whose product is 24 .

The ordered pairs are: $(1,24),(24,1),(2,12),(12,2),(3,8),(8,3),(4,6)$, and $(6,4)$

Hence, the possible orders of a matrix having 24 elements are:

$1 \times 24,24 \times 1,2 \times 12,12 \times 2,3 \times 8,8 \times 3,4 \times 6$, and $6 \times 4$

$(1,13)$ and $(13,1)$ are the ordered pairs of natural numbers whose product is 13 .

Hence, the possible orders of a matrix having 13 elements are $1 \times 13$ and $13 \times 1$.

3. If a matrix has 18 elements, what are the possible orders it can have? What, if it has 5 elements?

Solution

We know that if a matrix is of the order $m \times n$, it has $m n$ elements. Thus, to find all the possible orders of a matrix having 18 elements, we have to find all the ordered pairs of natural numbers whose product is 18 .

The ordered pairs are: $(1,18),(18,1),(2,9),(9,2),(3,6$,$) , and (6,3)$

Hence, the possible orders of a matrix having 18 elements are:

$1 \times 18,18 \times 1,2 \times 9,9 \times 2,3 \times 6$, and $6 \times 3$

$(1,5)$ and $(5,1)$ are the ordered pairs of natural numbers whose product is 5 .

Hence, the possible orders of a matrix having 5 elements are $1 \times 5$ and $5 \times 1$.

4. Construct a $2 \times 2$ matrix, $A=[a_{i j}]$, whose elements are given by:

(i) $a_{i j}=\frac{(i+j)^{2}}{2}$

(ii) $a_{i j}=\frac{i}{j}$

(iii) $a_{i j}=\frac{(i+2 j)^{2}}{2}$

Solution

(i) Since it is a $2 \times 2$ matrix it has 2 rows and 2 column. Let matrix be $\mathrm{A}$ Where $A=\left[\begin{array}{ll}a_{11} & a_{12} \ a_{21} & a_{22}\end{array}\right]$ Now it is given that $$ a_{i j}=\frac{(i+j)^2}{2} $$

$$ \begin{array}{|c|c|c|} \hline a_{i j} & i=, j= & a_{i j}=\frac{(i+j)^2}{2} \\ \hline a_{11} & i=1, j=1 & a_{11}=\frac{(1+1)^2}{2}=\frac{(2)^2}{2}=\frac{4}{2}=2 \\ \hline a_{12} & i=1, j=2 & a_{12}=\frac{(1+2)^2}{2}=\frac{(3)^2}{2}=\frac{9}{2} \\ \hline a_{21} & i=2, j=1 & a_{21}=\frac{(2+1)^2}{2}=\frac{(3)^2}{2}=\frac{9}{2} \\ \hline a_{22} & i=2, j=2 & a_{22}=\frac{(2+2)^2}{2}=\frac{(4)^2}{2}=\frac{16}{2}=8\\ \hline \end{array} $$

Hence, the required matrix $\mathrm{A}$ ia $A\left[\begin{array}{ll}a_{11} & a_{12} \ a_{21} & a_{22}\end{array}\right]=\left[\begin{array}{cc}2 & \frac{9}{2} \ \frac{9}{2} & 8\end{array}\right]$ (ii) Since it is a $2 \times 2$ matrix it has 2 rows and 2 column.

Let matrix be A Where $A=\left[\begin{array}{ll}a_{11} & a_{12} \ a_{21} & a_{22}\end{array}\right]$ Now it is given that $\mathrm{a}_{\mathrm{ij}}=\frac{\mathrm{i}}{\mathrm{j}}$

$$ \begin{array}{|c|c|c|} \hline \mathrm{a} _{\mathrm{ij}} & \mathrm{i}=, \mathrm{j}= & \mathrm{a} _{\mathrm{ij}}=\frac{\mathrm{i}}{\mathrm{j}} \\ \hline \mathrm{a} _{11} & \mathrm{i}=1, \mathrm{j}=1 & \mathrm{a} _{11}=\frac{1}{1}=1 \\ \hline \mathrm{a} _{12} & \mathrm{i}=1, \mathrm{j}=2 & \mathrm{a} _{12}=\frac{1}{2} \\ \hline \mathrm{a} _{21} & \mathrm{i}=2, \mathrm{j}=1 & \mathrm{a} _{21}=\frac{2}{1}=2 \\ \hline \mathrm{a} _{22} & \mathrm{i}=2, \mathrm{j}=2 & \mathrm{a} _{22}=\frac{2}{2}=1 \\ \hline \end{array} $$

Hence, the required matrix $\mathrm{A}$ is $$ A\left[\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right]=\left[\begin{array}{ll} 1 & \frac{1}{2} \\ 2 & 1 \\ \end{array}\right] $$

(iii) Since it is a $2 \times 2$ matrix it has 2 rows and 2 column. Let matrix be $\mathrm{A}$ Where $A=\left[\begin{array}{ll}a_{11} & a_{12} \\ a_{21} & a_{22}\end{array}\right]$ Now it is given that $$ a_{i j}=\frac{(i+2 j)^2}{2} $$

$$ \begin{array}{|c|c|c|} \hline a_{i j} & i=, j= & a_{i j}=\frac{(i+2 j)^2}{2} \\ \hline a_{11} & i=1, j=1 & a_{11}=\frac{(1+2(1))^2}{2}=\frac{(1+2)^2}{2}=\frac{(3)^2}{2}=\frac{9}{2} \\ \hline a_{12} & i=1, j=2 & a_{12}=\frac{(1+2(2))^2}{2}=\frac{(1+4)^2}{2}=\frac{(5)^2}{2}=\frac{25}{2} \\ \hline a_{21} & i=2, j=1 & a_{21}=\frac{(2+2(1))^2}{2}=\frac{(2+2)^2}{2}=\frac{(4)^2}{2}=\frac{16}{2}=8 \\ \hline a_{22} & i=2, j=2 & a_{22}=\frac{(2+2(2))^2}{2}=\frac{(2+4)^2}{2}=\frac{(6)^2}{2}=\frac{36}{2}=18 \\ \hline \end{array} $$

Hence, the required matrix $\mathrm{A}$ ia $$ A\left[\begin{array}{ll} \mathrm{a} _{11} & \mathrm{a} _{12} \\ \mathrm{a} _{21} & \mathrm{a} _{22} \end{array}\right]=\left[\begin{array}{cc} \frac{9}{2} & \frac{25}{2} \\ 8 & 18 \\ \end{array}\right] $$

5. Construct a $3 \times 4$ matrix, whose elements are given by:

$\begin{matrix}\text { (i) } a_{i j}=\frac{1}{2}|-3 i+j| & \text { (ii) } a_{i j}=2 i-j\end{matrix}$

Solution

In general, a $3 \times 4$ matrix is given by $A= \begin{cases} a _{11} & a _{12} & a _{13} & a _{14} \\ a _{21} & a _{22} & a _{23} & a _{24} \\ a _{31} & a _{32} & a _{33} & a _{34} \end{cases} $

(i) $a _{i j}=\frac{1}{2}|-3 i+j|, i=1,2,3$ and $j=1,2,3,4$

$ \begin{aligned} & \therefore a _{11}=\frac{1}{2}|-3 \times 1+1|=\frac{1}{2}|-3+1|=\frac{1}{2}|-2|=\frac{2}{2}=1 \\ & a _{21}=\frac{1}{2}|-3 \times 2+1|=\frac{1}{2}|-6+1|=\frac{1}{2}|-5|=\frac{5}{2} \\ & a _{31}=\frac{1}{2}|-3 \times 3+1|=\frac{1}{2}|-9+1|=\frac{1}{2}|-8|=\frac{8}{2}=4 \\ & a _{12}=\frac{1}{2}|-3 \times 1+2|=\frac{1}{2}|-3+2|=\frac{1}{2}|-1|=\frac{1}{2} \\ & a _{22}=\frac{1}{2}|-3 \times 2+2|=\frac{1}{2}|-6+2|=\frac{1}{2}|-4|=\frac{4}{2}=2 \\ & a _{32}=\frac{1}{2}|-3 \times 3+2|=\frac{1}{2}|-9+2|=\frac{1}{2}|-7|=\frac{7}{2} \\ & a _{13}=\frac{1}{2}|-3 \times 1+3|=\frac{1}{2}|-3+3|=0 \\ & a _{23}=\frac{1}{2}|-3 \times 2+3|=\frac{1}{2}|-6+3|=\frac{1}{2}|-3|=\frac{3}{2} \\ & a _{33}=\frac{1}{2}|-3 \times 3+3|=\frac{1}{2}|-9+3|=\frac{1}{2}|-6|=\frac{6}{2}=3 \\ & a _{14}=\frac{1}{2}|-3 \times 1+4|=\frac{1}{2}|-3+4|=\frac{1}{2}|1|=\frac{1}{2} \\ & a _{24}=\frac{1}{2}|-3 \times 2+4|=\frac{1}{2}|-6+4|=\frac{1}{2}|-2|=\frac{2}{2}=1 \\ & a _{34}=\frac{1}{2}|-3 \times 3+4|=\frac{1}{2}|-9+4|=\frac{1}{2}|-5|=\frac{5}{2} \end{aligned} $

Therefore, the required matrix is $A= \begin{cases} 1 & \frac{1}{2} & 0 & \frac{1}{2} \\ \frac{5}{2} & 2 & \frac{3}{2} & 1 \\ 4 & \frac{7}{2} & 3 & \frac{5}{2} \end{cases} $

(ii) $a _{i j}=2 i-j, i=1,2,3$ and $j=1,2,3,4$

$ \begin{aligned} & \therefore a _{11}=2 \times 1-1=2-1=1 \\ & a _{21}=2 \times 2-1=4-1=3 \\ & a _{31}=2 \times 3-1=6-1=5 \\ & a _{12}=2 \times 1-2=2-2=0 \\ & a _{22}=2 \times 2-2=4-2=2 \\ & a _{32}=2 \times 3-2=6-2=4 \\ & a _{13}=2 \times 1-3=2-3=-1 \\ & a _{23}=2 \times 2-3=4-3=1 \\ & a _{33}=2 \times 3-3=6-3=3 \\ & a _{14}=2 \times 1-4=2-4=-2 \\ & a _{24}=2 \times 2-4=4-4=0 \\ & a _{34}=2 \times 3-4=6-4=2 \end{aligned} $

Therefore, the required matrix is $A= \begin{cases} 1 & 0 & -1 & -2 \\ 3 & 2 & 1 & 0 \\ 5 & 4 & 3 & 2 \end{cases} $

6. Find the values of $x, y$ and $z$ from the following equations:

(i) $\begin{bmatrix}4 & 3 \\ x & 5\end{bmatrix}=\begin{bmatrix}y & z \\ 1 & 5\end{bmatrix}$

(ii) $\begin{bmatrix}x+y & 2 \\ 5+z & x y\end{bmatrix}=\begin{bmatrix}6 & 2 \\ 5 & 8\end{bmatrix}$

(iii)$\begin{bmatrix}x+y+z \\ x+z \\ y+z\end{bmatrix}=\begin{bmatrix}{l}9 \\ 5 \\ 7\end{bmatrix}$

Solution

(i) $\begin{bmatrix}4 & 3 \\ x & 5\end{bmatrix}=\begin{bmatrix}y & z \\ 1 & 5\end{bmatrix}$

As the given matrices are equal, their corresponding elements are also equal.

Comparing the corresponding elements, we get: $x=1, y=4$, and $z=3$

(ii) $\begin{bmatrix}x+y & 2 \\ 5+z & x y\end{bmatrix}=\begin{bmatrix}6 & 2 \\ 5 & 8\end{bmatrix}$

As the given matrices are equal, their corresponding elements are also equal.

Comparing the corresponding elements, we get:

$x+y=6, x y=8,5+z=5$

Now, $5+z=5 \Rightarrow z=0$

We know that:

$(x-y)^{2}=(x+y)^{2}-4 x y$

$\Rightarrow(x-y)^{2}=36-32=4$

$\Rightarrow x-y= \pm 2$

Now, when $x-y=2$ and $x+y=6$, we get $x=4$ and $y=2$

When $x-y=-2$ and $x+y=6$, we get $x=2$ and $y=4$

$\therefore x=4, y=2$, and $z=0$ or $x=2, y=4$, and $z=0$

(iii) $\begin{bmatrix}x+y+z \\ x+z \\ y+z\end{bmatrix}=\begin{bmatrix}{l}9 \\ 5 \\ 7\end{bmatrix}$

As the two matrices are equal, their corresponding elements are also equal.

Comparing the corresponding elements, we get:

$x+y+z=9$

$x+z=5$

$y+z=7$

From (1) and (2), we have:

$y+5=9$

$\Rightarrow y=4$

Then, from (3), we have:

$4+z=7$

$\Rightarrow z=3$

$\therefore x+z=5$

$\Rightarrow x=2$

$\therefore x=2, y=4$, and $z=3$

7. Find the value of $a, b, c$ and $d$ from the equation:

$$ \begin{bmatrix} a-b & 2 a+c \\ 2 a-b & 3 c+d \end{bmatrix}=\begin{bmatrix} -1 & 5 \\ 0 & 13 \end{bmatrix} $$

Solution

$ \begin{bmatrix} a-b & 2 a+c \\ 2 a-b & 3 c+d \end{bmatrix} = \begin{bmatrix} -1 & 5 \\ 0 & 13 \end{bmatrix} $

As the two matrices are equal, their corresponding elements are also equal.

Comparing the corresponding elements, we get:

$a-b=-1$

$2 a-b=0$

$2 a+c=5$

$3 c+d=13$

From (2), we have:

$b=2 a$

Then, from (1), we have:

$a-2 a=-1$

$\Rightarrow a=1$

$\Rightarrow b=2$

Now, from (3), we have:

$2 \times 1+c=5$

$\Rightarrow c=3$

From (4) we have:

$3 \times 3+d=13$

$\Rightarrow 9+d=13 \Rightarrow d=4$

$\therefore a=1, b=2, c=3$, and $d=4$

8. $A=[a_{i j}]_{m \times n 1}$ is a square matrix, if

(A) $m<n$

(B) $m>n$

(C) $m=n$

(D) None of these

Solution

The correct answer is $C$.

It is known that a given matrix is said to be a square matrix if the number of rows is equal to the number of columns.

Therefore, $A=[a _{i j}] _{m \times n}$ is a square matrix, if $m=n$.

9. Which of the given values of $x$ and $y$ make the following pair of matrices equal $\begin{bmatrix}3 x+7 & 5 \\ y+1 & 2-3 x\end{bmatrix},\begin{bmatrix}0 & y-2 \\ 8 & 4\end{bmatrix}$

(A) $x=\frac{-1}{3}, y=7$

(B) Not possible to find

(C) $y=7, \quad x=\frac{-2}{3}$

(D) $x=\frac{1}{3}, y=\frac{2}{3}$

Solution

The correct answer is B.

It is given that $ \begin{bmatrix} 3 x+7 & 5 \\ y+1 & 2-3 x\end{bmatrix} = \begin{bmatrix} 0 & y-2 \\ 8 & 4 \end{bmatrix} $

Equating the corresponding elements, we get:

$ \begin{aligned} & 3 x+7=0 \Rightarrow x=-\frac{7}{3} \\ & 5=y-2 \Rightarrow y=7 \\ & y+1=8 \Rightarrow y=7 \\ & 2-3 x=4 \Rightarrow x=-\frac{2}{3} \end{aligned} $

We find that on comparing the corresponding elements of the two matrices, we get two different values of $x$, which is not possible.

Hence, it is not possible to find the values of $x$ and $y$ for which the given matrices are equal.

10. The number of all possible matrices of order $3 \times 3$ with each entry 0 or 1 is:

(A) 27

(B) 18

(C) 81

(D) 512

Solution

The correct answer is D.

The given matrix of the order $3 \times 3$ has 9 elements and each of these elements can be either 0 or 1 .

Now, each of the 9 elements can be filled in two possible ways.

Therefore, by the multiplication principle, the required number of possible matrices is $2^{9}$ $=512$

3.3 Operations on Matrices

In this section, we shall introduce certain operations on matrices, namely, addition of matrices, multiplication of a matrix by a scalar, difference and multiplication of matrices.

3.3.1 Addition of matrices

Suppose Fatima has two factories at places A and B. Each factory produces sport shoes for boys and girls in three different price categories labelled 1,2 and 3. The quantities produced by each factory are represented as matrices given below:

Factory at A

Girls

$.\begin{bmatrix}{l}60 \\ 65 \\ 85\end{bmatrix}$

Factory at B

Suppose Fatima wants to know the total production of sport shoes in each price category. Then the total production

In category 1 : for boys $(80+90)$, for girls $(60+50)$

In category 2 : for boys $(75+70)$, for girls $(65+55)$

In category 3 : for boys $(90+75)$, for girls $(85+75)$

This can be represented in the matrix form as $\begin{bmatrix}80+90 & 60+50 \\ 75+70 & 65+55 \\ 90+75 & 85+75\end{bmatrix}$.

This new matrix is the sum of the above two matrices. We observe that the sum of two matrices is a matrix obtained by adding the corresponding elements of the given matrices. Furthermore, the two matrices have to be of the same order.

Thus, if $A=\begin{bmatrix}a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23}\end{bmatrix}$ is a $2 \times 3$ matrix and $B=\begin{bmatrix}b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23}\end{bmatrix}$ is another

$2 \times 3$ matrix. Then, we define $A+B=\begin{bmatrix}a_{11}+b_{11} & a_{12}+b_{12} & a_{13}+b_{13} \\ a_{21}+b_{21} & a_{22}+b_{22} & a_{23}+b_{23}\end{bmatrix}$.

In general, if $A=[a_{i j}]$ and $B=[b_{i j}]$ are two matrices of the same order, say $m \times n$. Then, the sum of the two matrices A and B is defined as a matrix $= [c _{ij}] _{m \times n} $, where $ c _{i j} = a _{ij} + b _{ij} $, for all possible values of i and j.

Example 6 Given $A=\begin{bmatrix}\sqrt{3} & 1 & -1 \\ 2 & 3 & 0\end{bmatrix}$ and $B=\begin{bmatrix}2 & \sqrt{5} & 1 \\ -2 & 3 & \frac{1}{2}\end{bmatrix}$, find $A+B$

Since A, B are of the same order $2 \times 3$. Therefore, addition of A and B is defined and is given by

$$ A+B=\begin{bmatrix} 2+\sqrt{3} & 1+\sqrt{5} & 1-1 \\ 2-2 & 3+3 & 0+\frac{1}{2} \end{bmatrix}=\begin{bmatrix} 2+\sqrt{3} & 1+\sqrt{5} & 0 \\ 0 & 6 & \frac{1}{2} \end{bmatrix} $$

Note

1. We emphasise that if A and B are not of the same order, then A + B is not defined. For example if $A=\begin{bmatrix}2 & 3 \\ 1 & 0\end{bmatrix}, B=\begin{bmatrix}1 & 2 & 3 \\ 1 & 0 & 1\end{bmatrix}$, then $A+B$ is not defined.

2. We may observe that addition of matrices is an example of binary operation on the set of matrices of the same order.

Multiplication of a matrix by a scalar

Now suppose that Fatima has doubled the production at a factory A in all categories (refer to 3.4.1).

Previously quantities (in standard units) produced by factory A were

$ \hspace{2mm} \text{Boys Girls} $

$\begin{matrix}1\\2\\3 \end{matrix} \begin{bmatrix}80 & 23\\ 75 & 60 \\90 & 65\end{bmatrix}$

Revised quantities produced by factory $A$ are as given below:

$ \quad \quad $Boys Girls

$\begin{matrix}1\\2\\3\end{matrix} \begin{bmatrix}2 \times 80 & 2 \times 60 \\ 2 \times 75 & 2 \times 65 \\ 2 \times 90 & 2 \times 85\end{bmatrix}$

This can be represented in the matrix form as $\begin{bmatrix}160 & 120 \\ 150 & 130 \\ 180 & 170\end{bmatrix}$. We observe that

the new matrix is obtained by multiplying each element of the previous matrix by 2 .

In general, we may define multiplication of a matrix by a scalar as follows: if $ A=[a_{ij}]_{m\times n} $ is a matrix and k is a scalar, then k A is another matrix which is obtained by multiplying each element of A by the scalar k.

In other words, $ kA = k[a_{ij}]_ {m\times n} $ $ =[k(a _{ij})] _{m\times n} $ that is, $ (i,j)^{th} $ element of kA is $ka _ {ij} $ for all possible values of i and j

For example, if $A=\begin{bmatrix}3 & 1 & 1.5 \\ \sqrt{5} & 7 & -3 \\ 2 & 0 & 5\end{bmatrix}$, then

$$ 3 A=3[\begin{bmatrix} 3 & 1 & 1.5 \\ \sqrt{5} & 7 & -3 \\ 2 & 0 & 5 \end{bmatrix}]=[\begin{bmatrix} 9 & 3 & 4.5 \\ 3 \sqrt{5} & 21 & -9 \\ 6 & 0 & 15 \end{bmatrix}] $$

Negative of a matrix The negative of a matrix is denoted by $-A$. We define $-A=(-1) A$.

For example, let

$$ \begin{aligned} A & =\begin{bmatrix} 3 & 1 \\ -5 & x \end{bmatrix}, \text { then }-A \text { is given by } \\ -A & =(-1) A=(-1)\begin{bmatrix} 3 & 1 \\ -5 & x \end{bmatrix}=\begin{bmatrix} -3 & -1 \\ 5 & -x \end{bmatrix} \end{aligned} $$

Difference of matrices If $A=[a_{i j}], B=[b_{i j}]$ are two matrices of the same order, say $m \times n$, then difference $A-B$ is defined as a matrix $D=[d_{i j}]$, where $d_{i j}=a_{i j}-b_{i j}$, for all value of $i$ and $j$. In other words, $D=A-B=A+(-1) B$, that is sum of the matrix $A$ and the matrix - B.

Example 7 If $A=\begin{bmatrix}1 & 2 & 3 \\ 2 & 3 & 1\end{bmatrix}$ and $B=\begin{bmatrix}3 & -1 & 3 \\ -1 & 0 & 2\end{bmatrix}$, then find $2 A-B$.

Solution We have

$$ \begin{aligned} & 2 A-B=2 \begin{bmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{bmatrix}-\begin{bmatrix} 3 & -1 & 3 \\ -1 & 0 & 2 \end{bmatrix} \\ & =\begin{bmatrix} 2 & 4 & 6 \\ 4 & 6 & 2 \end{bmatrix}+\begin{bmatrix} -3 & 1 & -3 \\ 1 & 0 & -2 \end{bmatrix} \\ & \begin{bmatrix} 2-3 & 4+1 & 6-3 \\ 4+1 & 6+0 & 2-2 \end{bmatrix}=\begin{bmatrix} -1 & 5 & 3 \\ 5 & 6 & 0 \end{bmatrix} \end{aligned} $$

Properties of matrix addition

The addition of matrices satisfy the following properties:

(i) Commutative Law If $A=[a_{i j}], B=[b_{i j}]$ are matrices of the same order, say $m \times n$, then $A+B=B+A$.

Now

$$ \begin{aligned} A+B & =[a_{i j}]+[b_{i j}]=[a_{i j}+b_{i j}] \\ & =[b_{i j}+a_{i j}] \text { (addition of numbers is commutative) } \\ & =([b_{i j}]+[a_{i j}])=B+A \end{aligned} $$

(ii) Associative Law For any three matrices $A=[a_{i j}], B=[b_{i j}], C=[c_{i j}]$ of the same order, say $m \times n,(A+B)+C=A+(B+C)$.

Now

$$ \begin{aligned} (A+B)+C & =([a_{i j}]+[b_{i j}])+[c_{i j}] \\ & =[a_{i j}+b_{i j}]+[c_{i j}]=[(a_{i j}+b_{i j})+c_{i j}] \\ & =[a_{i j}+(b_{i j}+c_{i j})] \quad(\text { Why? }) \\ & =[a_{i j}]+[(b_{i j}+c_{i j})]=[a_{i j}]+([b_{i j}]+[c_{i j}])=A+(B+C) \end{aligned} $$ (iii) Existence of additive identity Let $A=[a_{i j}]$ be an $m \times n$ matrix and $O$ be an $m \times n$ zero matrix, then $A+O=O+A=A$. In other words, $O$ is the additive identity for matrix addition.

(iv) The existence of additive inverse Let $A=[a_{ij}]_{m \times n}$

be any matrix, then we have another matrix as $-A=[-a_{ij}]_{m \times n}$ such that $A+(-A)=(-A)+A=O$. So $-A$ is the additive inverse of $A$ or negative of $A$.

Properties of scalar multiplication of a matrix

If $A=[a_{i j}]$ and $B=[b_{i j}]$ be two matrices of the same order, say $m \times n$, and $k$ and $l$ are scalars, then

(i) $k(A+B)=k A+k B$, (ii) $(k+l) A=k A+l A$

(ii) $k(A+B)=k([a_{i j}]+[b_{i j}])$

$$ \begin{aligned} & =k[a_{i j}+b_{i j}]=[k(a_{i j}+b_{i j})]=[(k a_{i j})+(k b_{i j})] \\ & =[k a_{i j}]+[k b_{i j}]=k[a_{i j}]+k[b_{i j}]=k A+k B \end{aligned} $$

(iii) $(k+l) A=(k+l)[a_{i j}]$

$$ =[(k+l) a_{i j}]+[k a_{i j}]+[l a_{i j}]=k[a_{i j}]+l[a_{i j}]=k A+l A $$

Example 8 If $A=\begin{bmatrix}8 & 0 \\ 4 & -2 \\ 3 & 6\end{bmatrix}$ and $B=\begin{bmatrix}2 & -2 \\ 4 & 2 \\ -5 & 1\end{bmatrix}$, then find the matrix $X$, such that

$2 A+3 X=5 B$.

Solution We have $2 A+3 X=5 B$

or $\hspace{17 mm}$$ 2 A+3 X-2 A=5 B-2 A $

or$\hspace{17 mm}$$2 A-2 A+3 X=5 B-2 A$ $\quad \quad$ (Matrix addition is commutative)

or$\hspace{17 mm}$$O+3 X=5 B-2 A$ $\hspace{17 mm}$(– 2A is the additive inverse of 2A)

or$\hspace{17 mm}$$3 X=5 B-2 A$ $\hspace{25 mm}$(O is the additive identity)

or $\hspace{17 mm}$$X=\frac{1}{3}(5 B-2 A)$

$$ X=\frac{1}{3}\begin{pmatrix}5\begin{bmatrix} 2 & -2 \\ 4 & 2 \\ -5 & 1 \end{bmatrix}-2\begin{bmatrix} 8 & 0 \\ 4 & -2 \\ 3 & 6 \end{bmatrix}\end{pmatrix}=\frac{1}{3}\begin{pmatrix}\begin{bmatrix} 10 & -10 \\ 20 & 10 \\ -25 & 5 \end{bmatrix}+\begin{bmatrix} -16 & 0 \\ -8 & 4 \\ -6 & -12 \end{bmatrix}\end{pmatrix} $$

$$ =\frac{1}{3}\begin{bmatrix} 10-16 & -10+0 \\ 20-8 & 10+4 \\ -25-6 & 5-12 \end{bmatrix}=\frac{1}{3}\begin{bmatrix} -6 & -10 \\ 12 & 14 \\ -31 & -7 \end{bmatrix}=\begin{bmatrix} -2 & \frac{-10}{3} \\ \\ 4 & \frac{14}{3} \\ \\ \frac{-31}{3} & \frac{-7}{3} \end{bmatrix} $$

Example 9 Find $X$ and $Y$, if $X+Y=\begin{bmatrix}5 & 2 \\ 0 & 9\end{bmatrix}$ and $X-Y=\begin{bmatrix}3 & 6 \\ 0 & -1\end{bmatrix}$.

Solution We have $(X+Y)+(X-Y)=\begin{bmatrix}5 & 2 \\ 0 & 9\end{bmatrix}+\begin{bmatrix}3 & 6 \\ 0 & -1\end{bmatrix}$.

or

$$ \begin{gathered} (X+X)+(Y-Y)=\begin{bmatrix} 8 & 8 \\ 0 & 8 \end{bmatrix} \Rightarrow 2 X=\begin{bmatrix} 8 & 8 \\ 0 & 8 \end{bmatrix} \\ X=\frac{1}{2}\begin{bmatrix} 8 & 8 \\ 0 & 8 \end{bmatrix}\begin{bmatrix} 4 & 4 \\ 0 & 4 \end{bmatrix} \end{gathered} $$

Also

$$ (X+Y)-(X-Y)=\begin{bmatrix} 5 & 2 \\ 0 & 9 \end{bmatrix}-\begin{bmatrix} 3 & 6 \\ 0 & -1 \end{bmatrix} $$

or

$$ (X-X)+(Y+Y)=\begin{bmatrix} 5-3 & 2-6 \\ 0 & 9+1 \end{bmatrix} \Rightarrow 2 Y=\begin{bmatrix} 2 & -4 \\ 0 & 10 \end{bmatrix} $$

or

$$ Y=\frac{1}{2}\begin{bmatrix} 2 & -4 \\ 0 & 10 \end{bmatrix}=\begin{bmatrix} 1 & -2 \\ 0 & 5 \end{bmatrix} $$

Example 10 Find the values of $x$ and $y$ from the following equation:

$$ 2\begin{bmatrix} x & 5 \\ 7 & y-3 \end{bmatrix}+\begin{bmatrix} 3 & -4 \\ 1 & 2 \end{bmatrix}=\begin{bmatrix} 7 & 6 \\ 15 & 14 \end{bmatrix} $$

Solution We have

$$ 2\begin{bmatrix} x & 5 \\ 7 & y-3 \end{bmatrix}+\begin{bmatrix} 3 & -4 \\ 1 & 2 \end{bmatrix}=\begin{bmatrix} 7 & 6 \\ 15 & 14 \end{bmatrix} \Rightarrow\begin{bmatrix} 2 x & 10 \\ 14 & 2 y-6 \end{bmatrix}+\begin{bmatrix} 3 & -4 \\ 1 & 2 \end{bmatrix}=\begin{bmatrix} 7 & 6 \\ 15 & 14 \end{bmatrix} $$

$$\begin{aligned} & \text { or }\begin{bmatrix} 2 x+3 & 10-4 \\ 14+1 & 2 y-6+2 \end{bmatrix}=\begin{bmatrix} 7 & 6 \\ 15 & 14 \end{bmatrix} \Rightarrow\begin{bmatrix} 2 x+3 & 6 \\ 15 & 2 y-4 \end{bmatrix}=\begin{bmatrix} 7 & 6 \\ 15 & 14 \end{bmatrix} \\ & \text { or } \quad 2 x+3=7 \quad \text { and } \quad 2 y-4=14 \quad \text { (Why?) } \\ & \text { or } \quad 2 x=7-3 \quad \text { and } \quad 2 y=18 \\ & \text { or } x=\frac{4}{2} \quad \text { and } \quad y=\frac{18}{2} \\ & \text { i.e. } x=2 \quad \text { and } \quad y=9 \text {. } \end{aligned} $$

Example 11 Two farmers Ramkishan and Gurcharan Singh cultivates only three varieties of rice namely Basmati, Permal and Naura. The sale (in Rupees) of these varieties of rice by both the farmers in the month of September and October are given by the following matrices $A$ and $B$.

September Sales (in Rupees)

$$ A=\begin{bmatrix} \text { Basmati } & \text { Permal } & \text { Naura } \\ 10,000 & 20,000 & 30,000 \\ 50,000 & 30,000 & 10,000 \end{bmatrix} \substack{ { }\\ \\ \substack{\text { Ramkishan } \\ \\ \text { Gurcharan Singh }}} $$

October Sales (in Rupees)

$$ B=\begin{bmatrix} \text { Basmati } & \text { Permal } & \text { Naura } \\ 5000 & 10,000 & 6000 \\ 20,000 & 10,000 & 10,000 \end{bmatrix} \substack{ { }\\ \\ \substack{\text { Ramkishan } \\ \\ \text { Gurcharan Singh }}} $$

(i) Find the combined sales in September and October for each farmer in each variety.

(ii) Find the decrease in sales from September to October.

(iii) If both farmers receive $2 %$ profit on gross sales, compute the profit for each farmer and for each variety sold in October.

Solution

(i) Combined sales in September and October for each farmer in each variety is given by

$$ A+B=\begin{bmatrix} \text { Basmati } & \text { Permal } & \text { Naura } \\ 15,000 & 30,000 & 36,000 \\ 70,000 & 40,000 & 20,000 \end{bmatrix} \substack{ { }\\ \\ \substack{\text { Ramkishan } \\ \\ \text { Gurcharan Singh }}} $$ (ii) Change in sales from September to October is given by

$$ A-B=\begin{bmatrix} \text { Basmati } & \text { Permal } & \text { Naura } \\ 5000 & 10,000 & 24,000 \\ 30,000 & 20,000 & 0 \end{bmatrix} \substack{ { }\\ \\ \substack{\text { Ramkishan } \\ \\ \text { Gurcharan Singh }}} $$

(iii) $2 %$ of $B=\frac{2}{100} \times B=0.02 \times B$

$$ =0.02\begin{bmatrix} \text { Basmati } & \text { Permal } & \text { Naura } \\ 5000 & 10,000 & 6000 \\ 20,000 & 10,000 & 10,000 \end{bmatrix} \substack{ { }\\ \\ \substack{\text { Ramkishan } \\ \\ \text { Gurcharan Singh }}} $$

$$ =\begin{bmatrix} \text { Basmati } & \text { Permal } & \text { Naura } \\ 100 & 200 & 120 \\ 400 & 200 & 200 \end{bmatrix} \substack{ { }\\ \\ \substack{\text { Ramkishan } \\ \\ \text { Gurcharan Singh }}} $$

Thus, in October Ramkishan receives ₹ 100, ₹ 200 and ₹ 120 as profit in the sale of each variety of rice, respectively, and Grucharan Singh receives profit of ₹ 400, ₹ 200 and ₹ 200 in the sale of each variety of rice, respectively.

Multiplication of matrices

Suppose Meera and Nadeem are two friends. Meera wants to buy 2 pens and 5 story books, while Nadeem needs 8 pens and 10 story books. They both go to a shop to enquire about the rates which are quoted as follows:

$$ \text { Pen - ₹ } 5 \text { each, story book - ₹ } 50 \text { each. } $$

How much money does each need to spend? Clearly, Meera needs ₹ $(5 \times 2+50 \times 5)$ that is ₹ 260 , while Nadeem needs $(8 \times 5+50 \times 10)$ ₹, that is ₹ 540 . In terms of matrix representation, we can write the above information as follows:

Requirements $\quad$Prices per piece (in Rupees) $\quad$Money needed (in Rupees)

$ \begin{bmatrix} 2 & 5 \\ 8 & 10 \end{bmatrix} \quad\quad\quad\quad\quad\quad\begin{bmatrix} 5 \\ 50 \end{bmatrix} \quad\quad\quad\quad\quad\quad\quad\begin{bmatrix}{l} 5 \times 2+5 \times 50 \\ 8 \times 5+10 \times 50 \end{bmatrix}=\begin{bmatrix} 260 \\ 540 \end{bmatrix} $

Suppose that they enquire about the rates from another shop, quoted as follows:

$$ \text { pen }-₹ 4 \text { each, story book }-₹ 40 \text { each. } $$

Now, the money required by Meera and Nadeem to make purchases will be respectively ₹ $(4 \times 2+40 \times 5)=₹ 208$ and ₹ $(8 \times 4+10 \times 40)=₹ 432$

Again, the above information can be represented as follows:

Requirements $\quad$Prices per piece (in Rupees) $\quad$Money needed (in Rupees)

$$ \begin{bmatrix} 2 & 5 \\ 8 & 10 \end{bmatrix} \quad\quad\quad\quad\quad\quad\begin{bmatrix} 4 \\ 40 \end{bmatrix} \quad\quad\quad\quad\quad\quad\quad\begin{bmatrix} 4 \times 2+40 \times 5 \\ 8 \times 4+10 \times 40 \end{bmatrix}=\begin{bmatrix} 208 \\ 432 \end{bmatrix} $$

Now, the information in both the cases can be combined and expressed in terms of matrices as follows:

Requirements $\quad$Prices per piece (in Rupees) $\quad$Money needed (in Rupees)

$\begin{aligned} {\begin{bmatrix} 2 & 5 \\ 8 & 10 \end{bmatrix} \quad\quad\quad\quad \begin{bmatrix} 5 & 4 \\ 50 & 40 \end{bmatrix} } \quad\quad\quad\quad\quad \begin{bmatrix} 5 \times 2+5 \times 50 & 4 \times 2+40 \times 5 \\ 8 \times 5+10 \times 50 & 8 \times 4+10 \times 40 \end{bmatrix} \\ = \begin{bmatrix} 260 & 208 \\ 540 & 432 \end{bmatrix} \end{aligned}$

The above is an example of multiplication of matrices. We observe that, for multiplication of two matrices A and B, the number of columns in A should be equal to the number of rows in B. Furthermore for getting the elements of the product matrix, we take rows of A and columns of B, multiply them element-wise and take the sum. Formally, we define multiplication of matrices as follows:

The product of two matrices A and B is defined if the number of columns of A is equal to the number of rows of $B$. Let $A=[a_{i j}]$ be an $m \times n$ matrix and $B=[b_{j k}]$ be an $n \times p$ matrix. Then the product of the matrices $A$ and $B$ is the matrix $C$ of order $m \times p$. To get the $(i, k)^{\text {th }}$ element $c_{i k}$ of the matrix C, we take the $i^{t h}$ row of A and $k^{\text {th }}$ column of $B$, multiply them elementwise and take the sum of all these products. In other words, if $A=[a _ {ij}] _ {m \times n}, B = [b _ {jk} ]_ {n \times p} $, then the $i^{th}$ row of A is $[a _ {i1} a_{i2} \ldots a _ {in}]$ and the $k^t {th}$ column of

B is $\begin{bmatrix}{c}b_{1 k} \\ b_{2 k} \\ \vdots \\ b_{n k}\end{bmatrix}$, then $c_{i k}=a_{i 1} b_{1 k}+a_{i 2} b_{2 k}+a_{i 3} b_{3 k}+\ldots+a_{i n} b_{n k}=\sum_{j=1}^{n} a_{i j} b_{j k}$.

The matrix $C=[c_{i k}]_{m \times p}$ is the product of $A$ and $B$.

For example, if $C=\begin{bmatrix}1 & -1 & 2 \\ 0 & 3 & 4\end{bmatrix}$ and $D=\begin{bmatrix}2 & 7 \\ -1 & 1 \\ 5 & -4\end{bmatrix}$, then the product $C D$ is defined and is given by $C D=\begin{bmatrix}1 & -1 & 2 \\ 0 & 3 & 4\end{bmatrix}\begin{bmatrix}2 & 7 \\ -1 & 1 \\ 5 & -4\end{bmatrix}$. This is a $2 \times 2$ matrix in which each entry is the sum of the products across some row of $C$ with the corresponding entries down some column of $D$. These four computations are

$\begin{aligned} & \text { Entry in } \\ & \text { first row } \\ & \text { first column }\end{aligned}\begin{bmatrix}1 & -1 & 2 \\ 0 & 3 & 4\end{bmatrix}\begin{bmatrix}2 & 7 \\ -1 & 1 \\ 5 & -4\end{bmatrix}=\begin{bmatrix}(1)(2)+(-1)(-1)+(2)(5) & ? \\ ? & ?\end{bmatrix}$

$\begin{aligned} & \text { Entry in } \\ & \text { first row } \\ & \text { second column }\end{aligned}\begin{bmatrix}1 & -1 & 2 \\ 0 & 3 & 4\end{bmatrix}\begin{bmatrix}2 & 7 \\ -1 & 1 \\ 5 & -4\end{bmatrix}=\begin{bmatrix}13 & (1)(7)+(-1)(1)+2(-4) \\ ? & ?\end{bmatrix}$

$\begin{aligned} & \text { Entry in } \\ & \text { second row } \\ & \text { first column }\end{aligned}\begin{bmatrix}1 & -1 & 2 \\ 0 & 3 & 4\end{bmatrix}\begin{bmatrix}2 & 7 \\ -1 & 1 \\ 5 & -4\end{bmatrix}=\begin{bmatrix}13 & -2 \\ 0(2)+3(-1)+4(5) & ?\end{bmatrix}$

$\begin{aligned} &\begin{bmatrix}\text { Entry in } \\ \text { second row } \\ \text { second column }\end{bmatrix}\end{aligned}\begin{bmatrix}1 & -1 & 2 \\ 0 & 3 & 4\end{bmatrix}\begin{bmatrix}2 & 7 \\ -1 & 1 \\ 5 & -4\end{bmatrix}=\begin{bmatrix}13 & -2 \\ 17 & 0(7)+3(1)+4(-4)\end{bmatrix}$

Thus $CD=\begin{bmatrix}13 & -2 \\ 17 & -13\end{bmatrix}$

Example 12 Find $AB$, if $A=\begin{bmatrix}6 & 9 \\ 2 & 3\end{bmatrix}$ and $B=\begin{bmatrix}2 & 6 & 0 \\ 7 & 9 & 8\end{bmatrix}$.

Solution The matrix A has 2 columns which is equal to the number of rows of B. Hence AB is defined. Now

$$\begin{aligned} AB & =\begin{bmatrix} 6(2)+9(7) & 6(6)+9(9) & 6(0)+9(8) \\ 2(2)+3(7) & 2(6)+3(9) & 2(0)+3(8) \end{bmatrix} \\ & =\begin{bmatrix} 12+63 & 36+81 & 0+72 \\ 4+21 & 12+27 & 0+24 \end{bmatrix}=\begin{bmatrix} 75 & 117 & 72 \\ 25 & 39 & 24 \end{bmatrix} \end{aligned} $$

Remark If $AB$ is defined, then $BA$ need not be defined. In the above example, $AB$ is defined but $BA$ is not defined because $B$ has 3 column while $A$ has only 2 (and not 3 ) rows. If $A, B$ are, respectively $m \times n, k \times l$ matrices, then both $AB$ and $BA$ are defined if and only if $n=k$ and $l=m$. In particular, if both $A$ and $B$ are square matrices of the same order, then both $AB$ and $BA$ are defined.

Non-commutativity of multiplication of matrices

Now, we shall see by an example that even if $AB$ and $BA$ are both defined, it is not necessary that $AB=BA$.

Example 13 If $A=\begin{bmatrix}1 & -2 & 3 \\ -4 & 2 & 5\end{bmatrix}$ and $B=\begin{bmatrix}2 & 3 \\ 4 & 5 \\ 2 & 1\end{bmatrix}$, then find $A B$, $B A$. Show that $AB \neq BA$.

Solution Since A is a $2 \times 3$ matrix and B is $3 \times 2$ matrix. Hence AB and BA are both defined and are matrices of order $2 \times 2$ and $3 \times 3$, respectively. Note that

$$\begin{aligned} & AB=\begin{bmatrix}{rcc} 1 & -2 & 3 \\ -4 & 2 & 5 \end{bmatrix}\begin{bmatrix} 2 & 3 \\ 4 & 5 \\ 2 & 1 \end{bmatrix}=\begin{bmatrix} 2-8+6 & 3-10+3 \\ -8+8+10 & -12+10+5 \end{bmatrix}=\begin{bmatrix} 0 & -4 \\ 10 & 3 \end{bmatrix} \\ & BA=\begin{bmatrix} 2 & 3 \\ 4 & 5 \\ 2 & 1 \end{bmatrix}\begin{bmatrix} 1 & -2 & 3 \\ -4 & 2 & 5 \end{bmatrix}=\begin{bmatrix} 2-12 & -4+6 & 6+15 \\ 4-20 & -8+10 & 12+25 \\ 2-4 & -4+2 & 6+5 \end{bmatrix}=\begin{bmatrix} -10 & 2 & 21 \\ -16 & 2 & 37 \\ -2 & -2 & 11 \end{bmatrix} \end{aligned} $$

Clearly $AB \neq BA$

In the above example both $AB$ and $BA$ are of different order and so $AB \neq BA$. But one may think that perhaps $A B$ and $B A$ could be the same if they were of the same order. But it is not so, here we give an example to show that even if AB and BA are of same order they may not be same.

Example 14 If $A=\begin{bmatrix}1 & 0 \\ 0 & -1\end{bmatrix}$ and $B=\begin{bmatrix}0 & 1 \\ 1 & 0\end{bmatrix}$, then $A B=\begin{bmatrix}0 & 1 \\ -1 & 0\end{bmatrix}$.

and

$$ BA=\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} . \text { Clearly } AB \neq BA . $$

Thus matrix multiplication is not commutative.

Note This does not mean that $AB \neq BA$ for every pair of matrices $A, B$ for which $AB$ and $BA$, are defined. For instance,

If $A=\begin{bmatrix}1 & 0 \\ 0 & 2\end{bmatrix}, B=\begin{bmatrix}3 & 0 \\ 0 & 4\end{bmatrix}$, then $A B=B A=\begin{bmatrix}3 & 0 \\ 0 & 8\end{bmatrix}$

Observe that multiplication of diagonal matrices of same order will be commutative.

Zero matrix as the product of two non zero matrices

We know that, for real numbers $a, b$ if $a b=0$, then either $a=0$ or $b=0$. This need not be true for matrices, we will observe this through an example.

Example 15 Find $A B$, if $A=\begin{bmatrix}0 & -1 \\ 0 & 2\end{bmatrix}$ and $B=\begin{bmatrix}3 & 5 \\ 0 & 0\end{bmatrix}$.

Solution We have $AB=\begin{bmatrix}0 & -1 \\ 0 & 2\end{bmatrix}\begin{bmatrix}3 & 5 \\ 0 & 0\end{bmatrix}=\begin{bmatrix}0 & 0 \\ 0 & 0\end{bmatrix}$.

Thus, if the product of two matrices is a zero matrix, it is not necessary that one of the matrices is a zero matrix.

Properties of multiplication of matrices

The multiplication of matrices possesses the following properties, which we state without proof.

1. The associative law For any three matrices $A, B$ and $C$. We have $(AB) C=A(BC)$, whenever both sides of the equality are defined.

2. The distributive law For three matrices $A, B$ and $C$.

(i) $A(B+C)=AB+AC$

(ii) $(A+B) C=AC+BC$, whenever both sides of equality are defined.

3. The existence of multiplicative identity For every square matrix A, there exist an identity matrix of same order such that $IA=AI=A$.

Now, we shall verify these properties by examples.

Example 16 If $A=\begin{bmatrix}1 & 1 & -1 \\ 2 & 0 & 3 \\ 3 & -1 & 2\end{bmatrix}, B=\begin{bmatrix}1 & 3 \\ 0 & 2 \\ -1 & 4\end{bmatrix}$ and $C=\begin{bmatrix}1 & 2 & 3 & -4 \\ 2 & 0 & -2 & 1\end{bmatrix}$, find $A(BC),(AB) C$ and show that $(AB) C=A(BC)$.

Solution We have

$A B=\begin{bmatrix}1 & 1 & -1 \\ 2 & 0 & 3 \\ 3 & -1 & 2\end{bmatrix}\begin{bmatrix}1 & 3 \\ 0 & 2 \\ -1 & 4\end{bmatrix}=\begin{bmatrix}1+0+1 & 3+2-4 \\ 2+0-3 & 6+0+12 \\ 3+0-2 & 9-2+8\end{bmatrix}=\begin{bmatrix}2 & 1 \\ -1 & 18 \\ 1 & 15\end{bmatrix}$

$(AB)(C)=\begin{bmatrix}2 & 1 \\ -1 & 18 \\ 1 & 15\end{bmatrix}\begin{bmatrix}1 & 2 & 3 & -4 \\ 2 & 0 & -2 & 1\end{bmatrix}=\begin{bmatrix}2+2 & 4+0 & 6-2 & -8+1 \\ -1+36 & -2+0 & -3-36 & 4+18 \\ 1+30 & 2+0 & 3-30 & -4+15\end{bmatrix}$

$=\begin{bmatrix}4 & 4 & 4 & -7 \\ 35 & -2 & -39 & 22 \\ 31 & 2 & -27 & 11\end{bmatrix}$

Now $\quad BC=\begin{bmatrix}1 & 3 \\ 0 & 2 \\ -1 & 4\end{bmatrix}\begin{bmatrix}1 & 2 & 3 & -4 \\ 2 & 0 & -2 & 1\end{bmatrix}=\begin{bmatrix}1+6 & 2+0 & 3-6 & -4+3 \\ 0+4 & 0+0 & 0-4 & 0+2 \\ -1+8 & -2+0 & -3-8 & 4+4\end{bmatrix}$

$$ =\begin{bmatrix} 7 & 2 & -3 & -1 \\ 4 & 0 & -4 & 2 \\ 7 & -2 & -11 & 8 \end{bmatrix} $$

Therefore $\quad A(BC)=\begin{bmatrix}1 & 1 & -1 \\ 2 & 0 & 3 \\ 3 & -1 & 2\end{bmatrix}\begin{bmatrix}7 & 2 & -3 & -1 \\ 4 & 0 & -4 & 2 \\ 7 & -2 & -11 & 8\end{bmatrix}$

$$\begin{aligned} & =\begin{bmatrix} 7+4-7 & 2+0+2 & -3-4+11 & -1+2-8 \\ 14+0+21 & 4+0-6 & -6+0-33 & -2+0+24 \\ 21-4+14 & 6+0-4 & -9+4-22 & -3-2+16 \end{bmatrix} \\ & =\begin{bmatrix} 4 & 4 & 4 & -7 \\ 35 & -2 & -39 & 22 \\ 31 & 2 & -27 & 11 \end{bmatrix} . \text { Clearly, (AB) C =A (BC) } \end{aligned} $$

Example 17 If $A=\begin{bmatrix}0 & 6 & 7 \\ -6 & 0 & 8 \\ 7 & -8 & 0\end{bmatrix}, B=\begin{bmatrix}0 & 1 & 1 \\ 1 & 0 & 2 \\ 1 & 2 & 0\end{bmatrix}, C=\begin{bmatrix}2 \\ -2 \\ 3\end{bmatrix}$

Calculate $AC, BC$ and $(A+B) C$. Also, verify that $(A+B) C=AC+BC$

Solution Now, $A+B=\begin{bmatrix}0 & 7 & 8 \\ -5 & 0 & 10 \\ 8 & -6 & 0\end{bmatrix}$

So $\quad(A+B) C=\begin{bmatrix}0 & 7 & 8 \\ -5 & 0 & 10 \\ 8 & -6 & 0\end{bmatrix}\begin{bmatrix}2 \\ -2 \\ 3\end{bmatrix}=\begin{bmatrix}0-14+24 \\ -10+0+30 \\ 16+12+0\end{bmatrix}=\begin{bmatrix}0 \\ 20 \\ 28\end{bmatrix}$

Further $\quad AC=\begin{bmatrix}0 & 6 & 7 \\ -6 & 0 & 8 \\ 7 & -8 & 0\end{bmatrix}\begin{bmatrix}2 \\ -2 \\ 3\end{bmatrix}=\begin{bmatrix}0-12+21 \\ -12+0+24 \\ 14+16+0\end{bmatrix}=\begin{bmatrix}9 \\ 12 \\ 30\end{bmatrix}$

and $\quad BC=\begin{bmatrix}0 & 1 & 1 \\ 1 & 0 & 2 \\ 1 & 2 & 0\end{bmatrix}\begin{bmatrix}2 \\ -2 \\ 3\end{bmatrix}=\begin{bmatrix}0-2+3 \\ 2+0+6 \\ 2-4+0\end{bmatrix}=\begin{bmatrix}1 \\ 8 \\ -2\end{bmatrix}$

So $\quad AC+BC=\begin{bmatrix}9 \\ 12 \\ 30\end{bmatrix}+\begin{bmatrix}1 \\ 8 \\ -2\end{bmatrix}=\begin{bmatrix}10 \\ 20 \\ 28\end{bmatrix}$

Clearly, $\quad(A+B) C=AC+BC$

Example 18 If $A=\begin{bmatrix}1 & 2 & 3 \\ 3 & -2 & 1 \\ 4 & 2 & 1\end{bmatrix}$, then show that $A^{3}-23 A-40 I=O$

Solution We have $A^{2}=A \cdot A=\begin{bmatrix}1 & 2 & 3 \\ 3 & -2 & 1 \\ 4 & 2 & 1\end{bmatrix}\begin{bmatrix}1 & 2 & 3 \\ 3 & -2 & 1 \\ 4 & 2 & 1\end{bmatrix}=\begin{bmatrix}19 & 4 & 8 \\ 1 & 12 & 8 \\ 14 & 6 & 15\end{bmatrix}$

So

$$ A^{3}=A A^{2}=\begin{bmatrix} 1 & 2 & 3 \\ 3 & -2 & 1 \\ 4 & 2 & 1 \end{bmatrix}\begin{bmatrix} 19 & 4 & 8 \\ 1 & 12 & 8 \\ 14 & 6 & 15 \end{bmatrix}=\begin{bmatrix} 63 & 46 & 69 \\ 69 & -6 & 23 \\ 92 & 46 & 63 \end{bmatrix} $$

Now

$$\begin{aligned} A^{3}-23 A-40 I & =\begin{bmatrix} 63 & 46 & 69 \\ 69 & -6 & 23 \\ 92 & 46 & 63 \end{bmatrix}-23\begin{bmatrix} 1 & 2 & 3 \\ 3 & -2 & 1 \\ 4 & 2 & 1 \end{bmatrix}-40\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \\ & =\begin{bmatrix} 63 & 46 & 69 \\ 69 & -6 & 23 \\ 92 & 46 & 63 \end{bmatrix}+\begin{bmatrix} -23 & -46 & -69 \\ -69 & 46 & -23 \\ -92 & -46 & -23 \end{bmatrix}+\begin{bmatrix} -40 & 0 & 0 \\ 0 & -40 & 0 \\ 0 & 0 & -40 \end{bmatrix} \\ & =\begin{bmatrix} 63-23-40 & 46-46+0 & 69-69+0 \\ 69-69+0 & -6+46-40 & 23-23+0 \\ 92-92+0 & 46-46+0 & 63-23-40 \end{bmatrix} \\ & =\begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}=O \end{aligned} $$

Example 19 In a legislative assembly election, a political group hired a public relations firm to promote its candidate in three ways: telephone, house calls, and letters. The cost per contact (in paise) is given in matrix $A$ as

$$ A=\text { Cost per contact } \\ \quad\quad\quad\quad \begin{bmatrix} 40 \\ 100 \\ 50 \end{bmatrix} \large{\substack{ {}\\ \\ \substack{\text { Telephone } \\ \\ \text { House Call } \\ \\ \text { Letter }}}} $$

The number of contacts of each type made in two cities $X$ and $Y$ is given by Telephone $\quad$ Housecall $\quad$ Letter

$B=\begin{bmatrix}1000 & 500 & 5000 \\ 3000 & 1000 & 10,000\end{bmatrix} \rightarrow \large{\substack{ {} \substack{ X \\ \\ Y}}}$ Find the total amount spent by the group in the two cities $X$ and $Y$.

Solution We have

$$\begin{aligned} BA & =\begin{bmatrix} 40,000+50,000+250,000 \\ 120,000+100,000+500,000 \end{bmatrix} \rightarrow \large{\substack{ {} \substack{ X \\ \\ Y}}} \\ & =\begin{bmatrix} 340,000 \\ 720,000 \end{bmatrix} \rightarrow \large{\substack{ {} \substack{ X \\ \\ Y}}} \end{aligned} $$

So the total amount spent by the group in the two cities is 340,000 paise and 720,000 paise, i.e., $₹ 3400$ and $₹ 7200$, respectively.

EXERCISE 3.2

1. Let $A=\begin{bmatrix}2 & 4 \\ 3 & 2\end{bmatrix}, B=\begin{bmatrix}1 & 3 \\ -2 & 5\end{bmatrix}, C=\begin{bmatrix}-2 & 5 \\ 3 & 4\end{bmatrix}$

Find each of the following:

(i) $A+B$ $\quad$ (ii) $A-B$ $\quad$ (iii) $3 A-C$

(iv) $AB$ $\quad$ (v) $BA$

Solution

(i) $\quad A+B= \begin{bmatrix} 2 & 4 \\ 3 & 2\end{bmatrix} + \begin{bmatrix} 1 & 3 \\ -2 & 5\end{bmatrix} = \begin{bmatrix} 2+1 & 4+3 \\ 3-2 & 2+5\end{bmatrix} = \begin{bmatrix} 3 & 7 \\ 1 & 7 \end{bmatrix} $

(ii) $A-B= \begin{bmatrix} 2 & 4 \\ 3 & 2\end{bmatrix} - \begin{bmatrix} 1 & 3 \\ -2 & 5 \end{bmatrix} =$ (iii) $3 A-C=3 \begin{bmatrix} 2 & 4 \\ 3 & 2\end{bmatrix} - \begin{bmatrix} -2 & 5 \\ 3 & 4 \end{bmatrix} $

$= \begin{bmatrix} 3 \times 2 & 3 \times 4 \\ 3 \times 3 & 3 \times 2\end{bmatrix} - \begin{bmatrix} -2 & 5 \\ 3 & 4 \end{bmatrix} $

$= \begin{bmatrix} 6 & 12 \\ 9 & 6\end{bmatrix} - \begin{bmatrix} -2 & 5 \\ 3 & 4 \end{bmatrix} $

$= \begin{bmatrix} 6+2 & 12-5 \\ 9-3 & 6-4 \end{bmatrix} $

$= \begin{bmatrix} 8 & 7 \\ 6 & 2 \end{bmatrix} $

(iv) Matrix $A$ has 2 columns. This number is equal to the number of rows in matrix $B$.

Therefore, $A B$ is defined as:

$ \begin{aligned} A B & = \begin{bmatrix} 2 & 4 \\ 3 & 2 \end{bmatrix} \begin{bmatrix} 1 & 3 \\ -2 & 5 \end{bmatrix} = \begin{bmatrix} 2(1)+4(-2) & 2(3)+4(5) \\ 3(1)+2(-2) & 3(3)+2(5) \end{bmatrix} \\ & = \begin{bmatrix} 2-8 & 6+20 \\ 3-4 & 9+10 \end{bmatrix} = \begin{bmatrix} -6 & 26 \\ -1 & 19 \end{bmatrix} \end{aligned} $

(v) Matrix $B$ has 2 columns. This number is equal to the number of rows in matrix $A$. Therefore, $B A$ is defined as:

$ \begin{aligned} B A & = \begin{bmatrix} 1 & 3 \\ -2 & 5 \end{bmatrix} \begin{bmatrix} 2 & 4 \\ 3 & 2 \end{bmatrix} = \begin{bmatrix} 1(2)+3(3) & 1(4)+3(2) \\ -2(2)+5(3) & -2(4)+5(2) \end{bmatrix} \\ & = \begin{bmatrix} 2+9 & 4+6 \\ -4+15 & -8+10 \end{bmatrix} = \begin{bmatrix} 11 & 10 \\ 11 & 2 \end{bmatrix} \end{aligned} $

2. Compute the following:

(i) $\begin{bmatrix}a & b \\ -b & a\end{bmatrix}+\begin{bmatrix}a & b \\ b & a\end{bmatrix}$ $\quad$ (ii) $\begin{bmatrix}a^{2}+b^{2} & b^{2}+c^{2} \\ a^{2}+c^{2} & a^{2}+b^{2}\end{bmatrix}+\begin{bmatrix}2 a b & 2 b c \\ -2 a c & -2 a b\end{bmatrix}$

(iii) $\begin{bmatrix}-1 & 4 & -6 \\ 8 & 5 & 16 \\ 2 & 8 & 5\end{bmatrix}+\begin{bmatrix}12 & 7 & 6 \\ 8 & 0 & 5 \\ 3 & 2 & 4\end{bmatrix}$ $\quad$ (iv) $\begin{bmatrix}\cos ^{2} x & \sin ^{2} x \\ \sin ^{2} x & \cos ^{2} x\end{bmatrix}+\begin{bmatrix}\sin ^{2} x & \cos ^{2} x \\ \cos ^{2} x & \sin ^{2} x\end{bmatrix}$

Solution

(i) $ \begin{bmatrix} a & b \\ -b & a\end{bmatrix} + \begin{bmatrix} a & b \\ b & a\end{bmatrix} = \begin{bmatrix} a+a & b+b \\ -b+b & a+a\end{bmatrix} = \begin{bmatrix} 2 a & 2 b \\ 0 & 2 a \end{bmatrix} $

(ii) $ \begin{bmatrix} a^{2}+b^{2} & b^{2}+c^{2} \\ a^{2}+c^{2} & a^{2}+b^{2}\end{bmatrix} + \begin{bmatrix} 2 a b & 2 b c \\ -2 a c & -2 a b \end{bmatrix} $

$ \begin{aligned} & = \begin{bmatrix} a^{2}+b^{2}+2 a b & b^{2}+c^{2}+2 b c \\ a^{2}+c^{2}-2 a c & a^{2}+b^{2}-2 a b \end{bmatrix} \\ & = \begin{bmatrix} (a+b)^{2} & (b+c)^{2} \\ (a-c)^{2} & (a-b)^{2} \end{bmatrix} \end{aligned} $

(iii) $ \begin{bmatrix} -1 & 4 & -6 \\ 8 & 5 & 16 \\ 2 & 8 & 5\end{bmatrix} + \begin{bmatrix} 12 & 7 & 6 \\ 8 & 0 & 5 \\ 3 & 2 & 4 \end{bmatrix} $

$= \begin{bmatrix} -1+12 & 4+7 & -6+6 \\ 8+8 & 5+0 & 16+5 \\ 2+3 & 8+2 & 5+4 \end{bmatrix} $

$= \begin{bmatrix} 11 & 11 & 0 \\ 16 & 5 & 21 \\ 5 & 10 & 9 \end{bmatrix} $

(iv) $ \begin{bmatrix} \cos ^{2} x & \sin ^{2} x \\ \sin ^{2} x & \cos ^{2} x\end{bmatrix} + \begin{bmatrix} \sin ^{2} x & \cos ^{2} x \\ \cos ^{2} x & \sin ^{2} x \end{bmatrix} $

$= \begin{bmatrix} \cos ^{2} x+\sin ^{2} x & \sin ^{2} x+\cos ^{2} x \\ \sin ^{2} x+\cos ^{2} x & \cos ^{2} x+\sin ^{2} x \end{bmatrix} $

$= \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix} \quad(\because \sin ^{2} x+\cos ^{2} x=1)$

3. Compute the indicated products.

(i) $\begin{bmatrix}a & b \\ -b & a\end{bmatrix}\begin{bmatrix}a & -b \\ b & a\end{bmatrix}$ (ii) $\begin{bmatrix}1 \\ 2 \\ 3\end{bmatrix}\begin{bmatrix}2 & 3 & 4\end{bmatrix}$ (iii) $\begin{bmatrix}1 & -2 \\ 2 & 3\end{bmatrix}\begin{bmatrix}1 & 2 & 3 \\ 2 & 3 & 1\end{bmatrix}$

(iv) $\begin{bmatrix}2 & 3 & 4 \\ 3 & 4 & 5 \\ 4 & 5 & 6\end{bmatrix}\begin{bmatrix}1 & -3 & 5 \\ 0 & 2 & 4 \\ 3 & 0 & 5\end{bmatrix}$ (v) $\begin{bmatrix}2 & 1 \\ 3 & 2 \\ -1 & 1\end{bmatrix}\begin{bmatrix}1 & 0 & 1 \\ -1 & 2 & 1\end{bmatrix}$

(vi) $\begin{bmatrix}3 & -1 & 3 \\ -1 & 0 & 2\end{bmatrix}\begin{bmatrix}2 & -3 \\ 1 & 0 \\ 3 & 1\end{bmatrix}$

Solution

(i) $ \begin{bmatrix} a & b \\ -b & a\end{bmatrix} \begin{bmatrix} a & -b \\ b & a \end{bmatrix} $

$= \begin{bmatrix} a(a)+b(b) & a(-b)+b(a) \\ -b(a)+a(b) & -b(-b)+a(a) \end{bmatrix} $

$= \begin{bmatrix} a^{2}+b^{2} & -a b+a b \\ -a b+a b & b^{2}+a^{2}\end{bmatrix} = \begin{bmatrix} a^{2}+b^{2} & 0 \\ 0 & a^{2}+b^{2} \end{bmatrix} $

(ii) $ \begin{bmatrix} 1 \\ 2 \\ 3\end{bmatrix} \begin{bmatrix} 2 & 3 & 4\end{bmatrix} = \begin{bmatrix} 1(2) & 1(3) & 1(4) \\ 2(2) & 2(3) & 2(4) \\ 3(2) & 3(3) & 3(4)\end{bmatrix} = \begin{bmatrix} 2 & 3 & 4 \\ 4 & 6 & 8 \\ 6 & 9 & 12 \end{bmatrix} $

(iii) $ \begin{bmatrix} 1 & -2 \\ 2 & 3\end{bmatrix} \begin{bmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{bmatrix} $

$ \begin{aligned} & = \begin{bmatrix} 1(1)-2(2) & 1(2)-2(3) & 1(3)-2(1) \\ 2(1)+3(2) & 2(2)+3(3) & 2(3)+3(1) \end{bmatrix} \\ & = \begin{bmatrix} 1-4 & 2-6 & 3-2 \\ 2+6 & 4+9 & 6+3 \end{bmatrix} = \begin{bmatrix} -3 & -4 & 1 \\ 8 & 13 & 9 \end{bmatrix} \end{aligned} $

(iv) $ \begin{bmatrix} 2 & 3 & 4 \\ 3 & 4 & 5 \\ 4 & 5 & 6\end{bmatrix} \begin{bmatrix} 1 & -3 & 5 \\ 0 & 2 & 4 \\ 3 & 0 & 5 \end{bmatrix} $

$= \begin{bmatrix} 2(1)+3(0)+4(3) & 2(-3)+3(2)+4(0) & 2(5)+3(4)+4(5) \\ 3(1)+4(0)+5(3) & 3(-3)+4(2)+5(0) & 3(5)+4(4)+5(5) \\ 4(1)+5(0)+6(3) & 4(-3)+5(2)+6(0) & 4(5)+5(4)+6(5) \end{bmatrix} $

$= \begin{bmatrix} 2+0+12 & -6+6+0 & 10+12+20 \\ 3+0+15 & -9+8+0 & 15+16+25 \\ 4+0+18 & -12+10+0 & 20+20+30\end{bmatrix} = \begin{bmatrix} 14 & 0 & 42 \\ 18 & -1 & 56 \\ 22 & -2 & 70 \end{bmatrix} $

(v) $ \begin{bmatrix} 2 & 1 \\ 3 & 2 \\ -1 & 1\end{bmatrix} \begin{bmatrix} 1 & 0 & 1 \\ -1 & 2 & 1 \end{bmatrix} $

$= \begin{bmatrix} 2(1)+1(-1) & 2(0)+1(2) & 2(1)+1(1) \\ 3(1)+2(-1) & 3(0)+2(2) & 3(1)+2(1) \\ -1(1)+1(-1) & -1(0)+1(2) & -1(1)+1(1) \end{bmatrix} $

$= \begin{bmatrix} 2-1 & 0+2 & 2+1 \\ 3-2 & 0+4 & 3+2 \\ -1-1 & 0+2 & -1+1\end{bmatrix} = \begin{bmatrix} 1 & 2 & 3 \\ 1 & 4 & 5 \\ -2 & 2 & 0 \end{bmatrix} $

(vi) $ \begin{bmatrix} 3 & -1 & 3 \\ -1 & 0 & 2\end{bmatrix} \begin{bmatrix} 2 & -3 \\ 1 & 0 \\ 3 & 1 \end{bmatrix} $

$ \begin{aligned} & = \begin{bmatrix} 3(2)-1(1)+3(3) & 3(-3)-1(0)+3(1) \\ -1(2)+0(1)+2(3) & -1(-3)+0(0)+2(1) \end{bmatrix} \\ & = \begin{bmatrix} 6-1+9 & -9-0+3 \\ -2+0+6 & 3+0+2 \end{bmatrix} = \begin{bmatrix} 14 & -6 \\ 4 & 5 \end{bmatrix} \end{aligned} $

4. If $A=\begin{bmatrix}1 & 2 & -3 \\ 5 & 0 & 2 \\ 1 & -1 & 1\end{bmatrix}, B=\begin{bmatrix}3 & -1 & 2 \\ 4 & 2 & 5 \\ 2 & 0 & 3\end{bmatrix}$ and $C=\begin{bmatrix}4 & 1 & 2 \\ 0 & 3 & 2 \\ 1 & -2 & 3\end{bmatrix}$, then compute $(A+B)$ and $(B-C)$. Also, verify that $A+(B-C)=(A+B)-C$.

Solution

$ \begin{aligned} A+B & = \begin{bmatrix} 1 & 2 & -3 \\ 5 & 0 & 2 \\ 1 & -1 & 1 \end{bmatrix} + \begin{bmatrix} 3 & -1 & 2 \\ 4 & 2 & 5 \\ 2 & 0 & 3 \end{bmatrix} \\ & = \begin{bmatrix} 1+3 & 2-1 & -3+2 \\ 5+4 & 0+2 & 2+5 \\ 1+2 & -1+0 & 1+3 \end{bmatrix} = \begin{bmatrix} 4 & 1 & -1 \\ 9 & 2 & 7 \\ 3 & -1 & 4 \end{bmatrix} \\ B-C & = \begin{bmatrix} 3 & -1 & 2 \\ 4 & 2 & 5 \\ 2 & 0 & 3 \end{bmatrix} - \begin{bmatrix} 4 & 1 & 2 \\ 0 & 3 & 2 \\ 1 & -2 & 3 \end{bmatrix} \\ & = \begin{bmatrix} 3-4 & -1-1 & 2-2 \\ 4-0 & 2-3 & 5-2 \\ 2-1 & 0-(-2) & 3-3 \end{bmatrix} = \begin{bmatrix} -1 & -2 & 0 \\ 4 & -1 & 3 \\ 1 & 2 & 0 \end{bmatrix} \end{aligned} $

$ \begin{aligned} A+(B-C) & = \begin{bmatrix} 1 & 2 & -3 \\ 5 & 0 & 2 \\ 1 & -1 & 1 \end{bmatrix} + \begin{bmatrix} -1 & -2 & 0 \\ 4 & -1 & 3 \\ 1 & 2 & 0 \end{bmatrix} \\ & = \begin{bmatrix} 1+(-1) & 2+(-2) & -3+0 \\ 5+4 & 0+(-1) & 2+3 \\ 1+1 & -1+2 & 1+0 \end{bmatrix} = \begin{bmatrix} 0 & 0 & -3 \\ 9 & -1 & 5 \\ 2 & 1 & 1 \end{bmatrix} \\ (A+B)-C & = \begin{bmatrix} 4 & 1 & -1 \\ 9 & 2 & 7 \\ 3 & -1 & 4 \end{bmatrix} - \begin{bmatrix} 4 & 1 & 2 \\ 0 & 3 & 2 \\ 1 & -2 & 3 \end{bmatrix} \\ & = \begin{bmatrix} 4-4 & 1-1 \\ 9-0 & 2-3 \\ 3-1 & -1-(-2) & 4-3 \end{bmatrix} \begin{bmatrix} 0 & 0 & -3 \\ 9 & -1 & 5 \\ 2 & 1 & 1 \end{bmatrix} \end{aligned} $

Hence, we have verified that $A+(B-C)=(A+B)-C$.

5. If $A=\begin{bmatrix}\frac{2}{3} & 1 & \frac{5}{3} \\ \frac{1}{3} & \frac{2}{3} & \frac{4}{3} \\ \frac{7}{3} & 2 & \frac{2}{3}\end{bmatrix}$ and $B=\begin{bmatrix}\frac{2}{5} & \frac{3}{5} & 1 \\ \frac{1}{5} & \frac{2}{5} & \frac{4}{5} \\ \frac{7}{5} & \frac{6}{5} & \frac{2}{5}\end{bmatrix}$, then compute $3 A-5 B$.

Solution

$ \begin{aligned} 3 A-5 B & =3 \begin{bmatrix} \frac{2}{3} & 1 & \frac{5}{3} \\ \frac{1}{3} & \frac{2}{3} & \frac{4}{3} \\ \frac{7}{3} & 2 & \frac{2}{3} \end{bmatrix} -5 \begin{bmatrix} \frac{2}{5} & \frac{3}{5} & 1 \\ \frac{1}{5} & \frac{2}{5} & \frac{4}{5} \\ \frac{7}{5} & \frac{6}{5} & \frac{2}{5} \end{bmatrix} \\ & = \begin{bmatrix} 2 & 3 & 5 \\ 1 & 2 & 4 \\ 7 & 6 & 2 \end{bmatrix} - \begin{bmatrix} 2 & 3 & 5 \\ 1 & 2 & 4 \\ 7 & 6 & 2 \end{bmatrix} = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} \end{aligned} $

6. Simplify $\cos \theta\begin{bmatrix}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta\end{bmatrix}+\sin \theta\begin{bmatrix}\sin \theta & -\cos \theta \\ \cos \theta & \sin \theta\end{bmatrix}$

Solution

$ \begin{aligned} & \cos \theta \begin{bmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{bmatrix} +\sin \theta \begin{bmatrix} \sin \theta & -\cos \theta \\ \cos \theta & \sin \theta \end{bmatrix} \\ & = \begin{bmatrix} \cos ^{2} \theta & \cos \theta \sin \theta \\ -\sin \theta \cos \theta & \cos ^{2} \theta \end{bmatrix} + \begin{bmatrix} \sin ^{2} \theta & -\sin \theta \cos \theta \\ \sin \theta \cos \theta & \sin ^{2} \theta \end{bmatrix} \\ & = \begin{bmatrix} \cos ^{2} \theta+\sin ^{2} \theta & \cos \theta \sin \theta-\sin \theta \cos \theta \\ -\sin \theta \cos \theta+\sin \theta \cos \theta & \cos ^{2} \theta+\sin ^{2} \theta \end{bmatrix} \\ & = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \quad(\because \cos ^{2} \theta+\sin ^{2} \theta=1) \end{aligned} $

7. Find $X$ and $Y$, if

(i) $X+Y=\begin{bmatrix}7 & 0 \\ 2 & 5\end{bmatrix}$ and $X-Y=\begin{bmatrix}3 & 0 \\ 0 & 3\end{bmatrix}$

(ii) $2 X+3 Y=\begin{bmatrix}2 & 3 \\ 4 & 0\end{bmatrix}$ and $3 X+2 Y=\begin{bmatrix}2 & -2 \\ -1 & 5\end{bmatrix}$

Solution

$ X-Y= \begin{bmatrix} 3 & 0 \\ 0 & 3 \end{bmatrix} $

Adding equations (1) and (2), we get:

$ \begin{aligned} & 2 X= \begin{bmatrix} 7 & 0 \\ 2 & 5 \end{bmatrix} + \begin{bmatrix} 3 & 0 \\ 0 & 3 \end{bmatrix} = \begin{bmatrix} 7+3 & 0+0 \\ 2+0 & 5+3 \end{bmatrix} = \begin{bmatrix} 10 & 0 \\ 2 & 8 \end{bmatrix} \\ & \therefore X=\frac{1}{2} \begin{bmatrix} 10 & 0 \\ 2 & 8 \end{bmatrix} = \begin{bmatrix} 5 & 0 \\ 1 & 4 \end{bmatrix} \end{aligned} $

Now, $X+Y= \begin{bmatrix} 7 & 0 \\ 2 & 5 \end{bmatrix} $

$\Rightarrow \begin{bmatrix} 5 & 0 \\ 1 & 4\end{bmatrix} +Y= \begin{bmatrix} 7 & 0 \\ 2 & 5 \end{bmatrix} $

$\Rightarrow Y= \begin{bmatrix} 7 & 0 \\ 2 & 5\end{bmatrix} - \begin{bmatrix} 5 & 0 \\ 1 & 4 \end{bmatrix} $

$\Rightarrow Y= \begin{bmatrix} 7-5 & 0-0 \\ 2-1 & 5-4 \end{bmatrix} $

$\therefore Y= \begin{bmatrix} 2 & 0 \\ 1 & 1 \end{bmatrix} $

(ii) $2 X+3 Y= \begin{bmatrix} 2 & 3 \\ 4 & 0 \end{bmatrix} $

$ 3 X+2 Y= \begin{bmatrix} 2 & -2 \\ -1 & 5 \end{bmatrix} $

Multiplying equation (3) with (2), we get:

$$ \begin{align} & 2(2 X+3 Y)=2 \begin{bmatrix} 2 & 3 \\ 4 & 0 \\ \end{bmatrix} \\ & \Rightarrow 4 X+6 Y= \begin{bmatrix} 4 & 6 \\ 8 & 0 \\ \end{bmatrix} \end{align} $$

Multiplying equation (4) with (3), we get:

$$ \begin{align*} & 3(3 X+2 Y)=3 \begin{bmatrix} 2 & -2 \\ -1 & 5 \\ \end{bmatrix} \\ & \Rightarrow 9 X+6 Y= \begin{bmatrix} 6 & -6 \\ -3 & 15 \\ \end{bmatrix} \tag{6} \end{align*} $$

From (5) and (6), we have:

$ \begin{aligned} & (4 X+6 Y)-(9 X+6 Y)= \begin{bmatrix} 4 & 6 \\ 8 & 0 \end{bmatrix} - \begin{bmatrix} 6 & -6 \\ -3 & 15 \end{bmatrix} \\ & \Rightarrow-5 X= \begin{bmatrix} 4-6 & 6-(-6) \\ 8-(-3) & 0-15 \end{bmatrix} = \begin{bmatrix} -2 & 12 \\ 11 & -15 \end{bmatrix} \\ & \therefore X=-\frac{1}{5} \begin{bmatrix} -2 & 12 \\ 11 & -15 \end{bmatrix} = \begin{bmatrix} \frac{2}{5} & -\frac{12}{5} \\ -\frac{11}{5} & 3 \end{bmatrix} \end{aligned} $

Now, $2 X+3 Y= \begin{bmatrix} 2 & 3 \\ 4 & 0 \end{bmatrix} $ $\Rightarrow 2 \begin{bmatrix} \frac{2}{5} & -\frac{12}{5} \\ -\frac{11}{5} & 3\end{bmatrix} +3 Y= \begin{bmatrix} 2 & 3 \\ 4 & 0 \end{bmatrix} $

$\Rightarrow \begin{bmatrix} \frac{4}{5} & -\frac{24}{5} \\ -\frac{22}{5} & 6\end{bmatrix} +3 Y= \begin{bmatrix} 2 & 3 \\ 4 & 0 \end{bmatrix} $

$\Rightarrow 3 Y= \begin{bmatrix} 2 & 3 \\ 4 & 0\end{bmatrix} - \begin{bmatrix} \frac{4}{5} & -\frac{24}{5} \\ -\frac{22}{5} & 6 \end{bmatrix} $

$\Rightarrow 3 Y= \begin{bmatrix} 2-\frac{4}{5} & 3+\frac{24}{5} \\ 4+\frac{22}{5} & 0-6\end{bmatrix} = \begin{bmatrix} \frac{6}{5} & \frac{39}{5} \\ \frac{42}{5} & -6 \end{bmatrix} $

$\therefore Y=\frac{1}{3} \begin{bmatrix} \frac{6}{5} & \frac{39}{5} \\ \frac{42}{5} & -6\end{bmatrix} = \begin{bmatrix} \frac{2}{5} & \frac{13}{5} \\ \frac{14}{5} & -2 \end{bmatrix} $

8. Find $X$, if $Y=\begin{bmatrix}3 & 2 \\ 1 & 4\end{bmatrix}$ and $2 X+Y=\begin{bmatrix}1 & 0 \\ -3 & 2\end{bmatrix}$

Solution

$ \begin{aligned} & 2 X+Y= \begin{bmatrix} 1 & 0 \\ -3 & 2 \end{bmatrix} \\ & \Rightarrow 2 X+ \begin{bmatrix} 3 & 2 \\ 1 & 4 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ -3 & 2 \end{bmatrix} \\ & \Rightarrow 2 X= \begin{bmatrix} 1 & 0 \\ -3 & 2 \end{bmatrix} - \begin{bmatrix} 3 & 2 \\ 1 & 4 \end{bmatrix} = \begin{bmatrix} 1-3 & 0-2 \\ -3-1 & 2-4 \end{bmatrix} \\ & \Rightarrow 2 X= \begin{bmatrix} -2 & -2 \\ -4 & -2 \end{bmatrix} \\ & \therefore X=\frac{1}{2} \begin{bmatrix} -2 & -2 \\ -4 & -2 \end{bmatrix} = \begin{bmatrix} -1 & -1 \\ -2 & -1 \end{bmatrix} \end{aligned} $

9. Find $x$ and $y$, if $2\begin{bmatrix}1 & 3 \\ 0 & x\end{bmatrix}+\begin{bmatrix}y & 0 \\ 1 & 2\end{bmatrix}=\begin{bmatrix}5 & 6 \\ 1 & 8\end{bmatrix}$

Solution

$ \begin{aligned} & 2 \begin{bmatrix} 1 & 3 \\ 0 & x \end{bmatrix} + \begin{bmatrix} y & 0 \\ 1 & 2 \end{bmatrix} = \begin{bmatrix} 5 & 6 \\ 1 & 8 \end{bmatrix} \\ & \Rightarrow \begin{bmatrix} 2 & 6 \\ 0 & 2 x \end{bmatrix} + \begin{bmatrix} y & 0 \\ 1 & 2 \end{bmatrix} = \begin{bmatrix} 5 & 6 \\ 1 & 8 \end{bmatrix} \\ & \Rightarrow \begin{bmatrix} 2+y & 6 \\ 1 & 2 x+2 \end{bmatrix} = \begin{bmatrix} 5 & 6 \\ 1 & 8 \end{bmatrix} \end{aligned} $

Comparing the corresponding elements of these two matrices, we have:

$ \begin{aligned} & 2+y=5 \\ & \Rightarrow y=3 \\ & 2 x+2=8 \\ & \Rightarrow x=3 \\ & \therefore x=3 \text{ and } y=3 \end{aligned} $

10. Solve the equation for $x, y, z$ and $t$, if $2\begin{bmatrix}x & z \\ y & t\end{bmatrix}+3\begin{bmatrix}1 & -1 \\ 0 & 2\end{bmatrix}=3\begin{bmatrix}3 & 5 \\ 4 & 6\end{bmatrix}$

Solution

$ \begin{aligned} & 2 \begin{bmatrix} x & z \\ y & t \end{bmatrix} +3 \begin{bmatrix} 1 & -1 \\ 0 & 2 \end{bmatrix} =3 \begin{bmatrix} 3 & 5 \\ 4 & 6 \end{bmatrix} \\ & \Rightarrow \begin{bmatrix} 2 x & 2 z \\ 2 y & 2 t \end{bmatrix} + \begin{bmatrix} 3 & -3 \\ 0 & 6 \end{bmatrix} = \begin{bmatrix} 9 & 15 \\ 12 & 18 \end{bmatrix} \\ & \Rightarrow \begin{bmatrix} 2 x+3 & 2 z-3 \\ 2 y & 2 t+6 \end{bmatrix} = \begin{bmatrix} 9 & 15 \\ 12 & 18 \end{bmatrix} \end{aligned} $

Comparing the corresponding elements of these two matrices, we get:

$ \begin{aligned} & 2 x+3=9 \\ & \Rightarrow 2 x=6 \\ & \Rightarrow x=3 \end{aligned} $

$2 y=12$

$\Rightarrow y=6$

$ \begin{aligned} & 2 z-3=15 \\ & \Rightarrow 2 z=18 \\ & \Rightarrow z=9 \end{aligned} $

$ \begin{aligned} & 2 t+6=18 \\ & \Rightarrow 2 t=12 \\ & \Rightarrow t=6 \end{aligned} $

$\therefore x=3, y=6, z=9$, and $t=6$

11. If $x\begin{bmatrix}2 \\ 3\end{bmatrix}+y\begin{bmatrix}{c}-1 \\ 1\end{bmatrix}=\begin{bmatrix}10 \\ 5\end{bmatrix}$, find the values of $x$ and $y$.

Solution

$ \begin{aligned} & x \begin{bmatrix} 2 \\ 3 \end{bmatrix} +y \begin{bmatrix} -1 \\ 1 \end{bmatrix} = \begin{bmatrix} 10 \\ 5 \end{bmatrix} \\ & \Rightarrow \begin{bmatrix} 2 x \\ 3 x \end{bmatrix} + \begin{bmatrix} -y \\ y \end{bmatrix} = \begin{bmatrix} 10 \\ 5 \end{bmatrix} \\ & \Rightarrow \begin{bmatrix} 2 x-y \\ 3 x+y \end{bmatrix} = \begin{bmatrix} 10 \\ 5 \end{bmatrix} \end{aligned} $

Comparing the corresponding elements of these two matrices, we get:

$2 x-y=10$ and $3 x+y=5$

Adding these two equations, we have:

$5 x=15$

$\Rightarrow x=3$

Now, $3 x+y=5$

$\Rightarrow y=5-3 x$

$\Rightarrow y=5-9=-4$

$\therefore x=3$ and $y=-4$

12. Given $3\begin{bmatrix}x & y \\ z & w\end{bmatrix}=\begin{bmatrix}x & 6 \\ -1 & 2 w\end{bmatrix}+\begin{bmatrix}4 & x+y \\ z+w & 3\end{bmatrix}$, find the values of $x, y, z$ and $w$.

Solution

$ \begin{aligned} & 3 \begin{bmatrix} x & y \\ z & w \end{bmatrix} = \begin{bmatrix} x & 6 \\ -1 & 2 w \end{bmatrix} + \begin{bmatrix} 4 & x+y \\ z+w & 3 \end{bmatrix} \\ & \Rightarrow \begin{bmatrix} 3 x & 3 y \\ 3 z & 3 w \end{bmatrix} = \begin{bmatrix} x+4 & 6+x+y \\ -1+z+w & 2 w+3 \end{bmatrix} \end{aligned} $

Comparing the corresponding elements of these two matrices, we get:

$ \begin{aligned} & 3 x=x+4 \\ & \Rightarrow 2 x=4 \\ & \Rightarrow x=2 \end{aligned} $

$3 y=6+x+y$

$\Rightarrow 2 y=6+x=6+2=8$

$\Rightarrow y=4$

$3 w=2 w+3$

$\Rightarrow w=3$

$3 z=-1+z+w$

$\Rightarrow 2 z=-1+w=-1+3=2$

$\Rightarrow z=1$

$\therefore x=2, y=4, z=1$, and $w=3$

13. If $F(x)=\begin{bmatrix}\cos x & -\sin x & 0 \\ \sin x & \cos x & 0 \\ 0 & 0 & 1\end{bmatrix}$, show that $F(x) F(y)=F(x+y)$.

Solution

$ \begin{aligned} & F(x)= \begin{bmatrix} \cos x & -\sin x & 0 \\ \sin x & \cos x & 0 \\ 0 & 0 & 1 \end{bmatrix} , F(y)= \begin{bmatrix} \cos y & -\sin y & 0 \\ \sin y & \cos y & 0 \\ 0 & 0 & 1 \end{bmatrix} \\ & F(x+y)= \begin{bmatrix} \cos (x+y) & -\sin (x+y) & 0 \\ \sin (x+y) & \cos (x+y) & 0 \\ 0 & 0 & 1 \end{bmatrix} \\ & F(x) F(y) \\ & = \begin{bmatrix} \cos x & -\sin x & 0 \\ \sin x & \cos x & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \cos y & -\sin y & 0 \\ \sin y & \cos y & 0 \\ 0 & 0 & 1 \end{bmatrix} \\ & = \begin{bmatrix} \cos x \cos y-\sin x \sin y+0 & -\cos x \sin y-\sin x \cos y+0 & 0 \\ \sin x \cos y+\cos x \sin y+0 & -\sin x \sin y+\cos x \cos y+0 & 0 \\ 0 & 0 & 0 \end{bmatrix} \\ & = \begin{bmatrix} \cos (x+y) & -\sin (x+y) & 0 \\ \sin (x+y) & \cos (x+y) & 0 \\ 0 & 0 & 1 \end{bmatrix} \\ & =F(x+y) \\ & \therefore F(x) F(y)=F(x+y) \end{aligned} $

14. Show that

(i) $\begin{bmatrix}5 & -1 \\ 6 & 7\end{bmatrix}\begin{bmatrix}2 & 1 \\ 3 & 4\end{bmatrix} \neq\begin{bmatrix}2 & 1 \\ 3 & 4\end{bmatrix}\begin{bmatrix}5 & -1 \\ 6 & 7\end{bmatrix}$

(ii) $\begin{bmatrix}1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0\end{bmatrix}\begin{bmatrix}-1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4\end{bmatrix} \neq\begin{bmatrix}-1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4\end{bmatrix}\begin{bmatrix}1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0\end{bmatrix}$

Solution

(i) $ \begin{bmatrix} 5 & -1 \\ 6 & 7\end{bmatrix} \begin{bmatrix} 2 & 1 \\ 3 & 4 \end{bmatrix} $

$= \begin{bmatrix} 5(2)-1(3) & 5(1)-1(4) \\ 6(2)+7(3) & 6(1)+7(4) \end{bmatrix} $

$= \begin{bmatrix} 10-3 & 5-4 \\ 12+21 & 6+28\end{bmatrix} = \begin{bmatrix} 7 & 1 \\ 33 & 34 \end{bmatrix} $

$ \begin{bmatrix} 2 & 1 \\ 3 & 4\end{bmatrix} \begin{bmatrix} 5 & -1 \\ 6 & 7 \end{bmatrix} $

$= \begin{bmatrix} 2(5)+1(6) & 2(-1)+1(7) \\ 3(5)+4(6) & 3(-1)+4(7) \end{bmatrix} $

$= \begin{bmatrix} 10+6 & -2+7 \\ 15+24 & -3+28\end{bmatrix} = \begin{bmatrix} 16 & 5 \\ 39 & 25 \end{bmatrix} $

$\therefore \begin{bmatrix} 5 & -1 \\ 6 & 7\end{bmatrix} \begin{bmatrix} 2 & 1 \\ 3 & 4\end{bmatrix} \neq \begin{bmatrix} 2 & 1 \\ 3 & 4\end{bmatrix} \begin{bmatrix} 5 & -1 \\ 6 & 7 \end{bmatrix} $

(ii) $ \begin{bmatrix} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0\end{bmatrix} \begin{bmatrix} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{bmatrix} $

$= \begin{bmatrix} 1(-1)+2(0)+3(2) & 1(1)+2(-1)+3(3) & 1(0)+2(1)+3(4) \\ 0(-1)+1(0)+0(2) & 0(1)+1(-1)+0(3) & 0(0)+1(1)+0(4) \\ 1(-1)+1(0)+0(2) & 1(1)+1(-1)+0(3) & 1(0)+1(1)+0(4) \end{bmatrix} $

$= \begin{bmatrix} 5 & 8 & 14 \\ 0 & -1 & 1 \\ -1 & 0 & 1 \end{bmatrix} $

$ \begin{aligned} & { \begin{bmatrix} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{bmatrix} \begin{bmatrix} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{bmatrix} } \\ & = \begin{bmatrix} -1(1)+1(0)+0(1) & -1(2)+1(1)+0(1) & -1(3)+1(0)+0(0) \\ 0(1)+(-1)(0)+1(1) & 0(2)+(-1)(1)+1(1) & 0(3)+(-1)(0)+1(0) \\ 2(1)+3(0)+4(1) & 2(2)+3(1)+4(1) & 2(3)+3(0)+4(0) \end{bmatrix} \\ & = \begin{bmatrix} -1 & -1 & -3 \\ 1 & 0 & 0 \\ 6 & 11 & 6 \end{bmatrix} \\ & \therefore \begin{bmatrix} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{bmatrix} \begin{bmatrix} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{bmatrix} \neq \begin{bmatrix} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{bmatrix} \begin{bmatrix} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{bmatrix} \end{aligned} $

15. Find $A^{2}-5 A+6 I$, if $A=\begin{bmatrix}2 & 0 & 1 \\ 2 & 1 & 3 \\ 1 & -1 & 0\end{bmatrix}$

Solution

We have $A^{2}=A \times A$

$ \begin{aligned} & A^{2}=A A= \begin{bmatrix} 2 & 0 & 1 \\ 2 & 1 & 3 \\ 1 & -1 & 0 \end{bmatrix} \begin{bmatrix} 2 & 0 & 1 \\ 2 & 1 & 3 \\ 1 & -1 & 0 \end{bmatrix} \\ & = \begin{bmatrix} 2(2)+0(2)+1(1) & 2(0)+0(1)+1(-1) & 2(1)+0(3)+1(0) \\ 2(2)+1(2)+3(1) & 2(0)+1(1)+3(-1) & 2(1)+1(3)+3(0) \\ 1(2)+(-1)(2)+0(1) & 1(0)+(-1)(1)+0(-1) & 1(1)+(-1)(3)+0(0) \end{bmatrix} \\ & = \begin{bmatrix} 4+0+1 & 0+0-1 & 2+0+0 \\ 4+2+3 & 0+1-3 & 2+3+0 \\ 2-2+0 & 0-1+0 & 1-3+0 \end{bmatrix} \\ & = \begin{bmatrix} 5 & -1 & 2 \\ 9 & -2 & 5 \\ 0 & -1 & -2 \end{bmatrix} \\ & \therefore A^{2}-5 A+6 I \\ & = \begin{bmatrix} 5 & -1 & 2 \\ 9 & -2 & 5 \\ 0 & -1 & -2 \end{bmatrix} -5 \begin{bmatrix} 2 & 0 & 1 \\ 2 & 1 & 3 \\ 1 & -1 & 0 \end{bmatrix} +6 \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \\ & = \begin{bmatrix} 5 & -1 & 2 \\ 9 & -2 & 5 \\ 0 & -1 & -2 \end{bmatrix} - \begin{bmatrix} 10 & 0 & 5 \\ 10 & 5 & 15 \\ 5 & -5 & 0 \end{bmatrix} + \begin{bmatrix} 6 & 0 & 0 \\ 0 & 6 & 0 \\ 0 & 0 & 6 \end{bmatrix} \\ & = \begin{bmatrix} 5-10 & -1-0 & 2-5 \\ 9-10 & -2-5 & 5-15 \\ 0-5 & -1+5 & -2-0 \end{bmatrix} + \begin{bmatrix} 6 & 0 & 0 \\ 0 & 6 & 0 \\ 0 & 0 & 6 \end{bmatrix} \\ & = \begin{bmatrix} -5 & -1 & -3 \\ -1 & -7 & -10 \\ -5 & 4 & -2 \end{bmatrix} + \begin{bmatrix} 6 & 0 & 0 \\ 0 & 6 & 0 \\ 0 & 0 & 6 \end{bmatrix} \\ & = \begin{bmatrix} -5+6 & -1+0 & -3+0 \\ -1+0 & -7+6 & -10+0 \\ -5+0 & 4+0 & -2+6 \end{bmatrix} \\ & = \begin{bmatrix} 1 & -1 & -3 \\ -1 & -1 & -10 \\ -5 & 4 & 4 \end{bmatrix} \end{aligned} $

16. If $A=\begin{bmatrix}1 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 0 & 3\end{bmatrix}$, prove that $A^{3}-6 A^{2}+7 A+2 I=0$

Solution

$ \begin{aligned} A^{2}=A A & = \begin{bmatrix} 1 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 0 & 3 \end{bmatrix} \begin{bmatrix} 1 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 0 & 3 \end{bmatrix} \\ & = \begin{bmatrix} 1+0+4 & 0+0+0 & 2+0+6 \\ 0+0+2 & 0+4+0 & 0+2+3 \\ 2+0+6 & 0+0+0 & 4+0+9 \end{bmatrix} = \begin{bmatrix} 5 & 0 & 8 \\ 2 & 4 & 5 \\ 8 & 0 & 13 \end{bmatrix} \end{aligned} $

Now $A^{3}=A^{2} \cdot A$

$ \begin{aligned} & = \begin{bmatrix} 5 & 0 & 8 \\ 2 & 4 & 5 \\ 8 & 0 & 13 \end{bmatrix} \begin{bmatrix} 1 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 0 & 3 \end{bmatrix} \\ & = \begin{bmatrix} 5+0+16 & 0+0+0 & 10+0+24 \\ 2+0+10 & 0+8+0 & 4+4+15 \\ 8+0+26 & 0+0+0 & 16+0+39 \end{bmatrix} \\ & = \begin{bmatrix} 21 & 0 & 34 \\ 12 & 8 & 23 \\ 34 & 0 & 55 \end{bmatrix} \\ & \therefore A^{3}-6 A^{2}+7 A+2 I \\ & = \begin{bmatrix} 21 & 0 & 34 \\ 12 & 8 & 23 \\ 34 & 0 & 55 \end{bmatrix} -6 \begin{bmatrix} 5 & 0 & 8 \\ 2 & 4 & 5 \\ 8 & 0 & 13 \end{bmatrix} +7 \begin{bmatrix} 1 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 0 & 3 \end{bmatrix} +2 \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{aligned} $

$ \begin{aligned} & = \begin{bmatrix} 21 & 0 & 34 \\ 12 & 8 & 23 \\ 34 & 0 & 55 \end{bmatrix} - \begin{bmatrix} 30 & 0 & 48 \\ 12 & 24 & 30 \\ 48 & 0 & 78 \end{bmatrix} + \begin{bmatrix} 7 & 0 & 14 \\ 0 & 14 & 7 \\ 14 & 0 & 21 \end{bmatrix} + \begin{bmatrix} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \end{bmatrix} \\ & = \begin{bmatrix} 21+7+2 & 0+0+0 & 34+14+0 \\ 12+0+0 & 8+14+2 & 23+7+0 \\ 34+14+0 & 0+0+0 & 55+21+2 \end{bmatrix} - \begin{bmatrix} 30 & 0 & 48 \\ 12 & 24 & 30 \\ 48 & 0 & 78 \end{bmatrix} \\ & = \begin{bmatrix} 30 & 0 & 48 \\ 12 & 24 & 30 \\ 48 & 0 & 78 \end{bmatrix} - \begin{bmatrix} 30 & 0 & 48 \\ 12 & 24 & 30 \\ 48 & 0 & 78 \end{bmatrix} \\ & = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} =O \\ & \therefore A^{3}-6 A^{2}+7 A+2 I=O \end{aligned} $

17. If $A=\begin{bmatrix}3 & -2 \\ 4 & -2\end{bmatrix}$ and $I=\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix}$, find $k$ so that $A^{2}=k A-2 I$

Solution

$ \begin{aligned} A^{2}=A \cdot A & = \begin{bmatrix} 3 & -2 \\ 4 & -2 \end{bmatrix} \begin{bmatrix} 3 & -2 \\ 4 & -2 \end{bmatrix} \\ & = \begin{bmatrix} 3(3)+(-2)(4) & 3(-2)+(-2)(-2) \\ 4(3)+(-2)(4) & 4(-2)+(-2)(-2) \end{bmatrix} = \begin{bmatrix} 1 & -2 \\ 4 & -4 \end{bmatrix} \end{aligned} $

Now $A^{2}=k A-2 I$

$ \begin{aligned} & \Rightarrow \begin{bmatrix} 1 & -2 \\ 4 & -4 \end{bmatrix} =k \begin{bmatrix} 3 & -2 \\ 4 & -2 \end{bmatrix} -2 \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \\ & \Rightarrow \begin{bmatrix} 1 & -2 \\ 4 & -4 \end{bmatrix} = \begin{bmatrix} 3 k & -2 k \\ 4 k & -2 k \end{bmatrix} - \begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix} \\ & \Rightarrow \begin{bmatrix} 1 & -2 \\ 4 & -4 \end{bmatrix} = \begin{bmatrix} 3 k-2 & -2 k \\ 4 k & -2 k-2 \end{bmatrix} \end{aligned} $

Comparing the corresponding elements, we have:

$3 k-2=1$

$\Rightarrow 3 k=3$

$\Rightarrow k=1$

Thus, the value of $k$ is 1 .

18. If $A=\begin{bmatrix}0 & -\tan \frac{\alpha}{2} \\ \tan \frac{\alpha}{2} & 0\end{bmatrix}$ and I is the identity matrix of order 2, show that

$I+A=(I-A)\begin{bmatrix}\cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha\end{bmatrix}$

Solution

On the L.H.S.

$I+A=\begin{bmatrix}1 & 0 \\ 0 & 1 \end{bmatrix} + \begin{bmatrix} 0 & -\tan \frac{\alpha}{2} \\ \tan \frac{\alpha}{2} & 0 \end{bmatrix}$

$=\begin{bmatrix} 0 & -\tan \frac{\alpha}{2} \\ \tan \frac{\alpha}{2} & 0 \end{bmatrix}\quad …(1)$

On the R.H.S.

$ (I-A) \begin{bmatrix} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{bmatrix} $

$=\begin{bmatrix}\begin{bmatrix} 1 & 0 \\0 & 1\end{bmatrix} - \begin{bmatrix} 0 & -\tan \frac{\alpha}{2} \\ \tan \frac{\alpha}{2} & 0 \end{bmatrix} \end{bmatrix} \begin{bmatrix} \cos \alpha & -\sin \beta \\ \sin \alpha & \cos \alpha \end{bmatrix}$

$=\begin{bmatrix} 1 & -\tan \frac{\alpha}{2} \\ \tan \frac{\alpha}{2} & 1 \end{bmatrix} \begin{bmatrix} \cos \alpha & -\sin \beta \\ \sin \alpha & \cos \alpha \end{bmatrix}$

$=\left[\begin{array}{ll}\cos \alpha+\sin \alpha \tan \frac{\alpha}{2} & -\sin \alpha+\cos \alpha \tan \frac{\alpha}{2} \\ -\cos \alpha \tan \frac{\alpha}{2}+\sin \alpha & \sin \alpha \tan \frac{\alpha}{2}+\cos \alpha\end{array}\right]$

$\begin{aligned} & =\left[\begin{array}{lc}1-2 \sin ^2 \frac{\alpha}{2}+2 \sin \frac{\alpha}{2} \cos \frac{\alpha}{2} \tan \frac{\alpha}{2} & -2 \sin \frac{\alpha}{2} \cos \frac{\alpha}{2}+\left(2 \cos ^2 \frac{\alpha}{2}-1\right) \tan \frac{\alpha}{2} \\ -\left(2 \cos ^2 \frac{\alpha}{2}-1\right) \tan \frac{\alpha}{2}+2 \sin \frac{\alpha}{2} \cos \frac{\alpha}{2} & 2 \sin \frac{\alpha}{2} \cos \frac{\alpha}{2} \tan \frac{\alpha}{2}+1-2 \sin ^2 \frac{\alpha}{2}\end{array}\right] \\ & =\left[\begin{array}{lc}1-2 \sin ^2 \frac{\alpha}{2}+2 \sin ^2 \frac{\alpha}{2} & -2 \sin \frac{\alpha}{2} \cos \frac{\alpha}{2}+2 \sin \frac{\alpha}{2} \cos \frac{\alpha}{2}-\tan \frac{\alpha}{2} \\ -2 \sin \frac{\alpha}{2} \cos \frac{\alpha}{2}+\tan \frac{\alpha}{2}+2 \sin \frac{\alpha}{2} \cos \frac{\alpha}{2} & 2 \sin ^2 \frac{\alpha}{2}+1-2 \sin ^2 \frac{\alpha}{2}\end{array}\right] \\ & =\left[\begin{array}{cc}1 & -\tan \frac{\alpha}{2} \\ \tan \frac{\alpha}{2} & 1\end{array}\right]\end{aligned}$

Thus, from (1) and (2), we get L.H.S. = R.H.S.

19. A trust fund has ₹ 30,000 that must be invested in two different types of bonds. The first bond pays 5% interest per year, and the second bond pays 7% interest per year. Using matrix multiplication, determine how to divide ₹ 30,000 among the two types of bonds. If the trust fund must obtain an annual total interest of: (a) ₹ 1800 (b) ₹ 2000

Solution

(a) Let Rs $x$ be invested in the first bond. Then, the sum of money invested in the second bond will be Rs $(30000-x)$.

It is given that the first bond pays $5 %$ interest per year and the second bond pays $7 %$ interest per year.

Therefore, in order to obtain an annual total interest of Rs 1800, we have:

$ \begin{aligned} & { \begin{bmatrix} x & (30000-x) \end{bmatrix} \begin{bmatrix} \frac{5}{100} \\ \frac{7}{100} \end{bmatrix} =1800 \quad[\text{ S.I. for 1 year }=\frac{\text{ Principal } \times \text{ Rate }}{100}]} \\ & \Rightarrow \frac{5 x}{100}+\frac{7(30000-x)}{100}=1800 \\ & \Rightarrow 5 x+210000-7 x=180000 \\ & \Rightarrow 210000-2 x=180000 \\ & \Rightarrow 2 x=210000-180000 \\ & \Rightarrow 2 x=30000 \\ & \Rightarrow x=15000 \end{aligned} $

Thus, in order to obtain an annual total interest of Rs 1800 , the trust fund should invest Rs 15000 in the first bond and the remaining Rs 15000 in the second bond.

(b) Let Rs $x$ be invested in the first bond. Then, the sum of money invested in the second bond will be Rs $(30000-x)$.

Therefore, in order to obtain an annual total interest of Rs 2000, we have:

$ \begin{bmatrix} x & (30000-x) \end{bmatrix} \begin{bmatrix} \frac{5}{100} \\ \frac{7}{100} \end{bmatrix} =2000 $

$\Rightarrow \frac{5 x}{100}+\frac{7(30000-x)}{100}=2000$

$\Rightarrow 5 x+210000-7 x=200000$

$\Rightarrow 210000-2 x=200000$

$\Rightarrow 2 x=210000-200000$

$\Rightarrow 2 x=10000$

$\Rightarrow x=5000$

Thus, in order to obtain an annual total interest of Rs 2000 , the trust fund should invest Rs 5000 in the first bond and the remaining Rs 25000 in the second bond.

20. The bookshop of a particular school has 10 dozen chemistry books, 8 dozen physics books, 10 dozen economics books. Their selling prices are ₹ 80 , ₹ 60 and $₹ 40$ each respectively. Find the total amount the bookshop will receive from selling all the books using matrix algebra.

Solution

The bookshop has 10 dozen chemistry books, 8 dozen physics books, and 10 dozen economics books.

The selling prices of a chemistry book, a physics book, and an economics book are respectively given as Rs 80, Rs 60, and Rs 40.

The total amount of money that will be received from the sale of all these books can be represented in the form of a matrix as:

$ \begin{aligned} & 12 \begin{bmatrix} 10 & 8 & 10 \end{bmatrix} \begin{bmatrix} 80 \\ 60 \\ 40 \end{bmatrix} \\ & =12[10 \times 80+8 \times 60+10 \times 40] \\ & =12(800+480+400) \\ & =12(1680) \\ & =20160 \end{aligned} $

Thus, the bookshop will receive Rs 20160 from the sale of all these books.

21. Assume X, Y, Z, W and P are matrices of order $2 \times n, 3 \times k, 2 \times p, n \times 3$ and $p \times k$, respectively. Choose the correct answer in Exercises 21 and 22.The restriction on $n, k$ and $p$ so that $PY+WY$ will be defined are: (A) $k=3, p=n$ (B) $k$ is arbitrary, $p=2$ (C) $p$ is arbitrary, $k=3$ (D) $k=2, p=3$

Solution

Matrices $P$ and $Y$ are of the orders $p \times k$ and $3 \times k$ respectively.

Therefore, matrix $P Y$ will be defined if $k=3$. Consequently, $P Y$ will be of the order $p \times k$. Matrices $W$ and $Y$ are of the orders $n \times 3$ and $3 \times k$ respectively.

Since the number of columns in $W$ is equal to the number of rows in $Y$, matrix $W Y$ is well-defined and is of the order $n \times k$.

Matrices $P Y$ and $W Y$ can be added only when their orders are the same.

However, $P Y$ is of the order $p \times k$ and $W Y$ is of the order $n \times k$. Therefore, we must have $p=n$.

Thus, $k=3$ and $p=n$ are the restrictions on $n, k$, and $p$ so that $P Y+W Y$ will be defined.

22. If $n=p$, then the order of the matrix $7 X-5 Z$ is: (A) $p \times 2$ (B) $2 \times n$ (C) $n \times 3$ (D) $p \times n$

Solution

The correct answer is $B$.

Matrix $X$ is of the order $2 \times n$.

Therefore, matrix $7 X$ is also of the same order.

Matrix $Z$ is of the order $2 \times p$, i.e., $2 \times n$ [Since $n=p$ ]

Therefore, matrix $5 Z$ is also of the same order.

Now, both the matrices $7 X$ and $5 Z$ are of the order $2 \times n$.

Thus, matrix $7 X-5 Z$ is well-defined and is of the order $2 \times n$.

Transpose of a Matrix

In this section, we shall learn about transpose of a matrix and special types of matrices such as symmetric and skew symmetric matrices.

Definition 3 If $A=[a_{i j}]$ be an $m \times n$ matrix, then the matrix obtained by interchanging the rows and columns of A is called the transpose of A. Transpose of the matrix A is denoted by $A^{\prime}$ or $(A^{T})$. In other words, if $A=[a _{i j}] _{m \times n}$, then $A^{\prime}=[a _{j i}] _{n \times m}$. For example,

if $A=\begin{bmatrix}3 & 5 \\ \sqrt{3} & 1 \\ 0 & \frac{-1}{5}\end{bmatrix}_{3 \times 2}$,

then $A^{\prime}=\begin{bmatrix}3 & \sqrt{3} & 0 \\ 5 & 1 & \frac{-1}{5}\end{bmatrix}_{2 \times 3}$

Properties of transpose of the matrices

We now state the following properties of transpose of matrices without proof. These may be verified by taking suitable examples.

For any matrices A and B of suitable orders, we have (i) $(A^{\prime})^{\prime}=A$, (ii) $(k A)^{\prime}=k A^{\prime}$ (where $k$ is any constant) (iii) $(A+B)^{\prime}=A^{\prime}+B^{\prime}$ (iv) $(A B)^{\prime}=B^{\prime} A^{\prime}$

Example 20 If $A=\begin{bmatrix}3 & \sqrt{3} & 2 \\ 4 & 2 & 0\end{bmatrix}$ and $B=\begin{bmatrix}2 & -1 & 2 \\ 1 & 2 & 4\end{bmatrix}$, verify that (i) $(A^{\prime})^{\prime}=A$, (ii) $(A+B)^{\prime}=A^{\prime}+B^{\prime}$,

(iii) $(k B)^{\prime}=k B^{\prime}$, where $k$ is any constant.

Solution

(i) We have

$$ A=\begin{bmatrix} 3 & \sqrt{3} & 2 \\ 4 & 2 & 0 \end{bmatrix} \Rightarrow A^{\prime}=\begin{bmatrix} 3 & 4 \\ \sqrt{3} & 2 \\ 2 & 0 \end{bmatrix} \Rightarrow(A^{\prime})^{\prime}=\begin{bmatrix} 3 & \sqrt{3} & 2 \\ 4 & 2 & 0 \end{bmatrix}=A $$

Thus $\quad(A^{\prime})^{\prime}=A$

(ii) We have

$$ A=\begin{bmatrix} 3 & \sqrt{3} & 2 \\ 4 & 2 & 0 \end{bmatrix}, B=\begin{bmatrix} 2 & -1 & 2 \\ 1 & 2 & 4 \end{bmatrix} \Rightarrow A+B=\begin{bmatrix} 5 & \sqrt{3}-1 & 4 \\ 5 & 4 & 4 \end{bmatrix} $$

Therefore $\quad(A+B)^{\prime}=\begin{bmatrix}5 & 5 \\ \sqrt{3}-1 & 4 \\ 4 & 4\end{bmatrix}$

Now $\quad A^{\prime}=\begin{bmatrix}3 & 4 \\ \sqrt{3} & 2 \\ 2 & 0\end{bmatrix}, B^{\prime}=\begin{bmatrix}2 & 1 \\ -1 & 2 \\ 2 & 4\end{bmatrix}$,

So $\quad A^{\prime}+B^{\prime}=\begin{bmatrix}5 & 5 \\ \sqrt{3}-1 & 4 \\ 4 & 4\end{bmatrix}$

Thus $\quad(A+B)^{\prime}=A^{\prime}+B^{\prime}$

(iii) We have

$$ k B=k\begin{bmatrix} 2 & -1 & 2 \\ 1 & 2 & 4 \end{bmatrix}=\begin{bmatrix} 2 k & -k & 2 k \\ k & 2 k & 4 k \end{bmatrix} $$

Then $\quad(k B)^{\prime}=\begin{bmatrix}2 k & k \\ -k & 2 k \\ 2 k & 4 k\end{bmatrix}=k\begin{bmatrix}2 & 1 \\ -1 & 2 \\ 2 & 4\end{bmatrix}=k B^{\prime}$

Thus

$$ (k B)^{\prime}=k B^{\prime} $$

Example 21 If $A=\begin{bmatrix}-2 \\ 4 \\ 5\end{bmatrix}, B=\begin{bmatrix}1 & 3 & -6\end{bmatrix}$, verify that $(A B)^{\prime}=B^{\prime} A^{\prime}$.

Solution We have

$$ A=\begin{bmatrix} -2 \\ 4 \\ 5 \end{bmatrix}, B=\begin{bmatrix} 1 & 3 & -6 \end{bmatrix} $$

then

$$ AB=\begin{bmatrix} -2 \\ 4 \\ 5 \end{bmatrix}\begin{bmatrix} 1 & 3 & -6 \end{bmatrix}=\begin{bmatrix} -2 & -6 & 12 \\ 4 & 12 & -24 \\ 5 & 15 & -30 \end{bmatrix} $$

Now

$$\begin{aligned} & A^{\prime}=\begin{bmatrix} -2 & 4 & 5 \end{bmatrix}, B^{\prime}=\begin{bmatrix} 1 \\ 3 \\ -6 \end{bmatrix} \\ & B^{\prime} A^{\prime}=\begin{bmatrix} 1 \\ 3 \\ -6 \end{bmatrix}\begin{bmatrix} -2 & 4 & 5 \end{bmatrix}=\begin{bmatrix} -2 & 4 & 5 \\ -6 & 12 & 15 \\ 12 & -24 & -30 \end{bmatrix}=(AB)^{\prime} \end{aligned} $$

Clearly

$$ (AB)^{\prime}=B^{\prime} A^{\prime} $$

Symmetric and Skew Symmetric Matrices

Definition 4 A square matrix $A=[a_{i j}]$ is said to be symmetric if $A^{\prime}=A$, that is, $[a_{i j}]=[a_{j i}]$ for all possible values of $i$ and $j$.

$$ \text { For example } A=\begin{bmatrix} \sqrt{3} & 2 & 3 \\ 2 & -1.5 & -1 \\ 3 & -1 & 1 \end{bmatrix} \text { is a symmetric matrix as } A^{\prime}=A $$

Definition 5 A square matrix $A=[a_{i j}]$ is said to be skew symmetric matrix if $A^{\prime}=-A$, that is $a_{j i}=-a_{i j}$ for all possible values of $i$ and $j$. Now, if we put $i=j$, we have $a_{i i}=-a_{i i}$. Therefore $2 a_{i i}=0$ or $a_{i i}=0$ for all $i$ ’s.

This means that all the diagonal elements of a skew symmetric matrix are zero.

For example, the matrix $B=\begin{bmatrix}0 & e & f \\ -e & 0 & g \\ -f & -g & 0\end{bmatrix}$ is a skew symmetric matrix as $B^{\prime}=-B$

Now, we are going to prove some results of symmetric and skew-symmetric matrices.

Theorem 1 For any square matrix $A$ with real number entries, $A+A^{\prime}$ is a symmetric matrix and $A-A^{\prime}$ is a skew symmetric matrix.

Proof Let $B=A+A^{\prime}$, then

$$\begin{aligned} B^{\prime} & =(A+A^{\prime})^{\prime} \\ & =A^{\prime}+(A^{\prime})^{\prime}(\text { as }(A+B)^{\prime}=A^{\prime}+B^{\prime}) \\ & =A^{\prime}+A(\text { as }(A^{\prime})^{\prime}=A) \\ & =A+A^{\prime}(\text { as } A+B=B+A) \\ & =B \end{aligned} $$

Therefore

$B=A+A^{\prime}$ is a symmetric matrix

Now let

$$ C=A-A^{\prime} $$

$$\begin{aligned} C^{\prime} & =(A-A^{\prime})^{\prime}=A^{\prime}-(A^{\prime})^{\prime} \quad \text { (Why?) } \\ & =A^{\prime}-A \quad(\text { Why? }) \\ & =-(A-A^{\prime})=-C \end{aligned} $$

Therefore

$$ C=A-A^{\prime} \text { is a skew symmetric matrix. } $$

Theorem 2 Any square matrix can be expressed as the sum of a symmetric and a skew symmetric matrix.

Proof Let A be a square matrix, then we can write

$$ A=\frac{1}{2}(A+A^{\prime})+\frac{1}{2}(A-A^{\prime}) $$

From the Theorem 1, we know that $(A+A^{\prime})$ is a symmetric matrix and $(A-A^{\prime})$ is a skew symmetric matrix. Since for any matrix $A,(k A)^{\prime}=k A^{\prime}$, it follows that $\frac{1}{2}(A+A^{\prime})$ is symmetric matrix and $\frac{1}{2}(A-A^{\prime})$ is skew symmetric matrix. Thus, any square matrix can be expressed as the sum of a symmetric and a skew symmetric matrix.

Example 22 Express the matrix $B=\begin{bmatrix}2 & -2 & -4 \\ -1 & 3 & 4 \\ 1 & -2 & -3\end{bmatrix}$ as the sum of a symmetric and a skew symmetric matrix.

Solution Here

$$ B^{\prime}=\begin{bmatrix} 2 & -1 & 1 \\ -2 & 3 & -2 \\ -4 & 4 & -3 \end{bmatrix} $$

Let

$$ P=\frac{1}{2}(B+B^{\prime})=\frac{1}{2}\begin{bmatrix} 4 & -3 & -3 \\ -3 & 6 & 2 \\ -3 & 2 & -6 \end{bmatrix}=\begin{bmatrix} 2 & \frac{-3}{2} & \frac{-3}{2} \\ \frac{-3}{2} & 3 & 1 \\ \frac{-3}{2} & 1 & -3 \end{bmatrix} $$

Now

$$ P^{\prime}=\begin{bmatrix} 2 & \frac{-3}{2} & \frac{-3}{2} \\ \frac{-3}{2} & 3 & 1 \\ \frac{-3}{2} & 1 & -3 \end{bmatrix}=P $$

Thus

$$ P=\frac{1}{2}(B+B^{\prime}) \text { is a symmetric matrix. } $$

Also, let $\quad Q=\frac{1}{2}(B-B^{\prime})=\frac{1}{2}\begin{bmatrix}0 & -1 & -5 \\ 1 & 0 & 6 \\ 5 & -6 & 0\end{bmatrix}=\begin{bmatrix}0 & \frac{-1}{2} & \frac{-5}{2} \\ \frac{1}{2} & 0 & 3 \\ \frac{5}{2} & -3 & 0\end{bmatrix}$

Then

$$ Q^{\prime}=\begin{bmatrix} 0 & \frac{1}{2} & \frac{5}{3} \\ \frac{-1}{2} & 0 & -3 \\ \frac{-5}{2} & 3 & 0 \end{bmatrix}=-Q $$

Thus

$$ Q=\frac{1}{2}(B-B^{\prime}) \text { is a skew symmetric matrix. } $$

Now

$$ P+Q=\begin{bmatrix} 2 & \frac{-3}{2} & \frac{-3}{2} \\ \frac{-3}{2} & 3 & 1 \\ \frac{-3}{2} & 1 & -3 \end{bmatrix}+\begin{bmatrix} 0 & \frac{-1}{2} & \frac{-5}{2} \\ \frac{1}{2} & 0 & 3 \\ \frac{5}{2} & -3 & 0 \end{bmatrix}=\begin{bmatrix} 2 & -2 & -4 \\ -1 & 3 & 4 \\ 1 & -2 & -3 \end{bmatrix}=B $$

Thus, B is represented as the sum of a symmetric and a skew symmetric matrix.

EXERCISE 3.3

1. Find the transpose of each of the following matrices:

(i) $\begin{bmatrix}5 \\ \frac{1}{2} \\ -1\end{bmatrix}$

(ii) $\begin{bmatrix}1 & -1 \\ 2 & 3\end{bmatrix}$

(iii) $\begin{bmatrix}-1 & 5 & 6 \\ \sqrt{3} & 5 & 6 \\ 2 & 3 & -1\end{bmatrix}$

Solution

(i) Let $A= \begin{bmatrix} 5 \\ \frac{1}{2} \\ -1\end{bmatrix} $, then $A^{T}= \begin{bmatrix} 5 & \frac{1}{2} & -1 \end{bmatrix} $

(ii) Let $A= \begin{bmatrix} 1 & -1 \\ 2 & 3\end{bmatrix} $, then $A^{T}= \begin{bmatrix} 1 & 2 \\ -1 & 3 \end{bmatrix} $

(iii) Let $A= \begin{bmatrix} -1 & 5 & 6 \\ \sqrt{3} & 5 & 6 \\ 2 & 3 & -1\end{bmatrix} $, then $A^{T}= \begin{bmatrix} -1 & \sqrt{3} & 2 \\ 5 & 5 & 3 \\ 6 & 6 & -1 \end{bmatrix} $

2. If $A=\begin{bmatrix}-1 & 2 & 3 \\ 5 & 7 & 9 \\ -2 & 1 & 1\end{bmatrix}$ and $B=\begin{bmatrix}-4 & 1 & -5 \\ 1 & 2 & 0 \\ 1 & 3 & 1\end{bmatrix}$, then verify that (i) $(A+B)^{\prime}=A^{\prime}+B^{\prime}$, (ii) $(A-B)^{\prime}=A^{\prime}-B^{\prime}$

Solution

We have: $A^{\prime}= \begin{bmatrix} -1 & 5 & -2 \\ 2 & 7 & 1 \\ 3 & 9 & 1\end{bmatrix} , B^{\prime}= \begin{bmatrix} -4 & 1 & 1 \\ 1 & 2 & 3 \\ -5 & 0 & 1 \end{bmatrix} $

(i) $A+B= \begin{bmatrix} -1 & 2 & 3 \\ 5 & 7 & 9 \\ -2 & 1 & 1\end{bmatrix} + \begin{bmatrix} -4 & 1 & -5 \\ 1 & 2 & 0 \\ 1 & 3 & 1\end{bmatrix} = \begin{bmatrix} -5 & 3 & -2 \\ 6 & 9 & 9 \\ -1 & 4 & 2 \end{bmatrix} $

$\therefore(A+B)^{\prime}= \begin{bmatrix} -5 & 6 & -1 \\ 3 & 9 & 4 \\ -2 & 9 & 2 \end{bmatrix} $

$A^{\prime}+B^{\prime}= \begin{bmatrix} -1 & 5 & -2 \\ 2 & 7 & 1 \\ 3 & 9 & 1\end{bmatrix} + \begin{bmatrix} -4 & 1 & 1 \\ 1 & 2 & 3 \\ -5 & 0 & 1\end{bmatrix} = \begin{bmatrix} -5 & 6 & -1 \\ 3 & 9 & 4 \\ -2 & 9 & 2 \end{bmatrix} $

Hence, we have verified that $(A+B)^{\prime}=A^{\prime}+B^{\prime}$

(ii) $A-B= \begin{bmatrix} -1 & 2 & 3 \\ 5 & 7 & 9 \\ -2 & 1 & 1\end{bmatrix} - \begin{bmatrix} -4 & 1 & -5 \\ 1 & 2 & 0 \\ 1 & 3 & 1\end{bmatrix} = \begin{bmatrix} 3 & 1 & 8 \\ 4 & 5 & 9 \\ -3 & -2 & 0 \end{bmatrix} $

$\therefore(A-B)^{\prime}= \begin{bmatrix} 3 & 4 & -3 \\ 1 & 5 & -2 \\ 8 & 9 & 0 \end{bmatrix} $

$A^{\prime}-B^{\prime}= \begin{bmatrix} -1 & 5 & -2 \\ 2 & 7 & 1 \\ 3 & 9 & 1\end{bmatrix} - \begin{bmatrix} -4 & 1 & 1 \\ 1 & 2 & 3 \\ -5 & 0 & 1\end{bmatrix} = \begin{bmatrix} 3 & 4 & -3 \\ 1 & 5 & -2 \\ 8 & 9 & 0 \end{bmatrix} $

Hence, we have verified that $(A-B)^{\prime}=A^{\prime}-B^{\prime}$.

3. If $A^{\prime}=\begin{bmatrix}3 & 4 \\ -1 & 2 \\ 0 & 1\end{bmatrix}$ and $B=\begin{bmatrix}-1 & 2 & 1 \\ 1 & 2 & 3\end{bmatrix}$, then verify that (i) $(A+B)^{\prime}=A^{\prime}+B^{\prime}$ (ii) $(A-B)^{\prime}=A^{\prime}-B^{\prime}$

Solution

(i) It is known that $A=(A^{\prime})^{\prime}$

Therefore, we have:

$ \begin{aligned} & A= \begin{bmatrix} 3 & -1 & 0 \\ 4 & 2 & 1 \end{bmatrix} \\ & B^{\prime}= \begin{bmatrix} -1 & 1 \\ 2 & 2 \\ 1 & 3 \end{bmatrix} \\ & A+B= \begin{bmatrix} 3 & -1 & 0 \\ 4 & 2 & 1 \end{bmatrix} + \begin{bmatrix} -1 & 2 & 1 \\ 1 & 2 & 3 \end{bmatrix} = \begin{bmatrix} 2 & 1 & 1 \\ 5 & 4 & 4 \end{bmatrix} \\ & \therefore(A+B)^{\prime}= \begin{bmatrix} 2 & 5 \\ 1 & 4 \\ 1 & 4 \end{bmatrix} \\ & A^{\prime}+B^{\prime}= \begin{bmatrix} 3 & 4 \\ -1 & 2 \\ 0 & 1 \end{bmatrix} + \begin{bmatrix} -1 & 1 \\ 2 & 2 \\ 1 & 3 \end{bmatrix} = \begin{bmatrix} 2 & 5 \\ 1 & 4 \\ 1 & 4 \end{bmatrix} \end{aligned} $

Thus, we have verified that $(A+B)^{\prime}=A^{\prime}+B^{\prime}$.

(ii) $A-B= \begin{bmatrix} 3 & -1 & 0 \\ 4 & 2 & 1\end{bmatrix} - \begin{bmatrix} -1 & 2 & 1 \\ 1 & 2 & 3\end{bmatrix} = \begin{bmatrix} 4 & -3 & -1 \\ 3 & 0 & -2 \end{bmatrix} $

$ \begin{aligned} & \therefore(A-B)^{\prime}= \begin{bmatrix} 4 & 3 \\ -3 & 0 \\ -1 & -2 \end{bmatrix} \\ & A^{\prime}-B^{\prime}= \begin{bmatrix} 3 & 4 \\ -1 & 2 \\ 0 & 1 \end{bmatrix} - \begin{bmatrix} -1 & 1 \\ 2 & 2 \\ 1 & 3 \end{bmatrix} = \begin{bmatrix} 4 & 3 \\ -3 & 0 \\ -1 & -2 \end{bmatrix} \end{aligned} $

Thus, we have verified that $(A-B)^{\prime}=A^{\prime}-B^{\prime}$.

4. If $A^{\prime}=\begin{bmatrix}-2 & 3 \\ 1 & 2\end{bmatrix}$ and $B=\begin{bmatrix}-1 & 0 \\ 1 & 2\end{bmatrix}$, then find $(A+2 B)^{\prime}$

Solution

We know that $A=(A^{\prime})^{\prime}$

$ \begin{aligned} & \therefore A= \begin{bmatrix} -2 & 1 \\ 3 & 2 \end{bmatrix} \\ & \therefore A+2 B= \begin{bmatrix} -2 & 1 \\ 3 & 2 \end{bmatrix} +2 \begin{bmatrix} -1 & 0 \\ 1 & 2 \end{bmatrix} = \begin{bmatrix} -2 & 1 \\ 3 & 2 \end{bmatrix} + \begin{bmatrix} -2 & 0 \\ 2 & 4 \end{bmatrix} = \begin{bmatrix} -4 & 1 \\ 5 & 6 \end{bmatrix} \\ & \therefore(A+2 B)^{\prime}= \begin{bmatrix} -4 & 5 \\ 1 & 6 \end{bmatrix} \end{aligned} $

5. For the matrices $A$ and $B$, verify that $(A B)^{\prime}=B^{\prime} A^{\prime}$, where (i) $A=\begin{bmatrix}1 \\ -4 \\ 3\end{bmatrix}, B=\begin{bmatrix}-1 & 2 & 1\end{bmatrix}$ (ii) $A=\begin{bmatrix}0 \\ 1 \\ 2\end{bmatrix}, B=\begin{bmatrix}1 & 5 & 7\end{bmatrix}$

Solution

$ \begin{aligned} & \text{ (i) } A B= \begin{bmatrix} 1 \\ -4 \\ 3 \end{bmatrix} \begin{bmatrix} -1 & 2 & 1 \end{bmatrix} = \begin{bmatrix} -1 & 2 & 1 \\ 4 & -8 & -4 \\ -3 & 6 & 3 \end{bmatrix} \\ & \therefore(A B)^{\prime}= \begin{bmatrix} -1 & 4 & -3 \\ 2 & -8 & 6 \\ 1 & -4 & 3 \end{bmatrix} \\ & \text{ Now, } A^{\prime}= \begin{bmatrix} 1 & -4 & 3 \end{bmatrix} , B^{\prime}= \begin{bmatrix} -1 \\ 2 \\ 1 \end{bmatrix} \\ & \therefore B^{\prime} A^{\prime}= \begin{bmatrix} -1 \\ 2 \\ 1 \end{bmatrix} \begin{bmatrix} 1 & -4 & 3 \end{bmatrix} = \begin{bmatrix} -1 & 4 & -3 \\ 2 & -8 & 6 \\ 1 & -4 & 3 \end{bmatrix} \end{aligned} $

Hence, we have verified that $(A B)^{\prime}=B^{\prime} A^{\prime}$.

(ii) $A B= \begin{bmatrix} 0 \\ 1 \\ 2\end{bmatrix} \begin{bmatrix} 1 & 5 & 7\end{bmatrix} = \begin{bmatrix} 0 & 0 & 0 \\ 1 & 5 & 7 \\ 2 & 10 & 14 \end{bmatrix} $

$\therefore(A B)^{\prime}= \begin{bmatrix} 0 & 1 & 2 \\ 0 & 5 & 10 \\ 0 & 7 & 14 \end{bmatrix} $

Now, $A^{\prime}= \begin{bmatrix} 0 & 1 & 2\end{bmatrix} , B^{\prime}= \begin{bmatrix} 1 \\ 5 \\ 7 \end{bmatrix} $

$\therefore B^{\prime} A^{\prime}= \begin{bmatrix} 1 \\ 5 \\ 7\end{bmatrix} \begin{bmatrix} 0 & 1 & 2\end{bmatrix} = \begin{bmatrix} 0 & 1 & 2 \\ 0 & 5 & 10 \\ 0 & 7 & 14 \end{bmatrix} $

Hence, we have verified that $(A B)^{\prime}=B^{\prime} A^{\prime}$.

6. If (i) $A=\begin{bmatrix}\cos \alpha & \sin \alpha \\ -\sin \alpha & \cos \alpha\end{bmatrix}$, then verify that $A^{\prime} A=I$

(ii) If $A=\begin{bmatrix}\sin \alpha & \cos \alpha \\ -\cos \alpha & \sin \alpha\end{bmatrix}$, then verify that $A^{\prime} A=I$

Solution

(i)

$ \begin{aligned} & A= \begin{bmatrix} \cos \alpha & \sin \alpha \\ -\sin \alpha & \cos \alpha \end{bmatrix} \\ & \therefore A^{\prime}= \begin{bmatrix} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{bmatrix} \\ & A^{\prime} A= \begin{bmatrix} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{bmatrix} \begin{bmatrix} \cos \alpha & \sin \alpha \\ -\sin \alpha & \cos \alpha \end{bmatrix} \\ & = \begin{bmatrix} (\cos \alpha)(\cos \alpha)+(-\sin \alpha)(-\sin \alpha) & (\cos \alpha)(\sin \alpha)+(-\sin \alpha)(\cos \alpha) \\ (\sin \alpha)(\cos \alpha)+(\cos \alpha)(-\sin \alpha) & (\sin \alpha)(\sin \alpha)+(\cos \alpha)(\cos \alpha) \end{bmatrix} \\ & = \begin{bmatrix} \cos 2 \alpha+\sin ^{2} \alpha & \sin \alpha \cos \alpha-\sin \alpha \cos \alpha \\ \sin \alpha \cos \alpha-\sin \alpha \cos \alpha & \sin ^{2} \alpha+\cos ^{2} \alpha \end{bmatrix} \\ & = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} =I \end{aligned} $

Hence, we have verified that $A^{\prime} A=I$.

(ii) $\quad A= \begin{cases} \sin \alpha & \cos \alpha \\ -\cos \alpha & \sin \alpha \end{cases} $

$ \begin{aligned} & \therefore A^{\prime}= \begin{bmatrix} \sin \alpha & -\cos \alpha \\ \cos \alpha & \sin \alpha \end{bmatrix} \\ & A^{\prime} A= \begin{bmatrix} \sin \alpha & -\cos \alpha \\ \cos \alpha & \sin \alpha \end{bmatrix} \begin{bmatrix} \sin \alpha & \cos \alpha \\ -\cos \alpha & \sin \alpha \end{bmatrix} \end{aligned} $

$ \begin{aligned} & { \begin{bmatrix} \sin \alpha & -\cos \alpha \\ \cos \alpha & \sin \alpha \end{bmatrix} \begin{bmatrix} \sin \alpha & \cos \alpha \\ -\cos \alpha & \sin \alpha \end{bmatrix} } \\ & = \begin{bmatrix} (\sin \alpha)(\sin \alpha)+(-\cos \alpha)(-\cos \alpha) & (\sin \alpha)(\cos \alpha)+(-\cos \alpha)(\sin \alpha) \\ (\cos \alpha)(\sin \alpha)+(\sin \alpha)(-\cos \alpha) & (\cos \alpha)(\cos \alpha)+(\sin \alpha)(\sin \alpha) \end{bmatrix} \\ & = \begin{bmatrix} \sin ^{2} \alpha+\cos ^{2} \alpha & \sin \alpha \cos \alpha-\sin \alpha \cos \alpha \\ \sin \alpha \cos \alpha-\sin \alpha \cos \alpha & \cos ^{2} \alpha+\sin ^{2} \alpha \end{bmatrix} \\ & = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} =I \end{aligned} $

Hence, we have verified that $A^{\prime} A=I$.

7. (i) Show that the matrix $A=\begin{bmatrix}1 & -1 & 5 \\ -1 & 2 & 1 \\ 5 & 1 & 3\end{bmatrix}$ is a symmetric matrix.

(ii) Show that the matrix $A=\begin{bmatrix}0 & 1 & -1 \\ -1 & 0 & 1 \\ 1 & -1 & 0\end{bmatrix}$ is a skew symmetric matrix.

Solution

(i) We have:

$ A^{\prime}= \begin{bmatrix} 1 & -1 & 5 \\ -1 & 2 & 1 \\ 5 & 1 & 3 \end{bmatrix} =A $

$\therefore A^{\prime}=A$

Hence, $A$ is a symmetric matrix.

(ii) We have:

$ A^{\prime}= \begin{bmatrix} 0 & -1 & 1 \\ 1 & 0 & -1 \\ -1 & 1 & 0 \end{bmatrix} =- \begin{bmatrix} 0 & 1 & -1 \\ -1 & 0 & 1 \\ 1 & -1 & 0 \end{bmatrix} =-A $

$\therefore A^{\prime}=-A$

Hence, $A$ is a skew-symmetric matrix.

8. For the matrix $A=\begin{bmatrix}1 & 5 \\ 6 & 7\end{bmatrix}$, verify that

(i) $(A+A^{\prime})$ is a symmetric matrix

(ii) $(A-A^{\prime})$ is a skew symmetric matrix

Solution

$ \begin{aligned} & A^{\prime}= \begin{bmatrix} 1 & 6 \\ 5 & 7 \end{bmatrix} \\ & \text{ (i) } A+A^{\prime}= \begin{bmatrix} 1 & 5 \\ 6 & 7 \end{bmatrix} + \begin{bmatrix} 1 & 6 \\ 5 & 7 \end{bmatrix} = \begin{bmatrix} 2 & 11 \\ 11 & 14 \end{bmatrix} \\ & \therefore(A+A^{\prime})^{\prime}= \begin{bmatrix} 2 & 11 \\ 11 & 14 \end{bmatrix} =A+A^{\prime} \end{aligned} $

Hence, $(A+A^{\prime})$ is a symmetric matrix.

(ii) $A-A^{\prime}= \begin{bmatrix} 1 & 5 \\ 6 & 7\end{bmatrix} - \begin{bmatrix} 1 & 6 \\ 5 & 7\end{bmatrix} = \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} $ $(A-A^{\prime})^{\prime}= \begin{bmatrix} 0 & 1 \\ -1 & 0\end{bmatrix} =- \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} =-(A-A^{\prime})$

Hence, $(A-A^{\prime})$ is a skew-symmetric matrix.

9. Find $\frac{1}{2}(A+A^{\prime})$ and $\frac{1}{2}(A-A^{\prime})$, when $A=\begin{bmatrix}0 & a & b \\ -a & 0 & c \\ -b & -c & 0\end{bmatrix}$

Solution

The given matrix is $A= \begin{bmatrix} 0 & a & b \\ -a & 0 & c \\ -b & -c & 0 \end{bmatrix} $

$\therefore A^{\prime}= \begin{bmatrix} 0 & -a & -b \\ a & 0 & -c \\ b & c & 0 \end{bmatrix} $

$A+A^{\prime}= \begin{bmatrix} 0 & a & b \\ -a & 0 & c \\ -b & -c & 0\end{bmatrix} + \begin{bmatrix} 0 & -a & -b \\ a & 0 & -c \\ b & c & 0\end{bmatrix} = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}$

$\therefore \frac{1}{2}(A+A^{\prime})= \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} $

Now, $A-A^{\prime}= \begin{bmatrix} 0 & a & b \\ -a & 0 & c \\ -b & -c & 0\end{bmatrix} - \begin{bmatrix} 0 & -a & -b \\ a & 0 & -c \\ b & c & 0\end{bmatrix} = \begin{bmatrix} 0 & 2 a & 2 b \\ -2 a & 0 & 2 c \\ -2 b & -2 c & 0 \end{bmatrix}$

$\therefore \frac{1}{2}(A-A^{\prime})= \begin{bmatrix} 0 & a & b \\ -a & 0 & c \\ -b & -c & 0 \end{bmatrix} $

10. Express the following matrices as the sum of a symmetric and a skew symmetric matrix: (i) $\begin{bmatrix}3 & 5 \\ 1 & -1\end{bmatrix}$ (ii) $\begin{bmatrix}6 & -2 & 2 \\ -2 & 3 & -1 \\ 2 & -1 & 3\end{bmatrix}$ (iii) $\begin{bmatrix}3 & 3 & -1 \\ -2 & -2 & 1 \\ -4 & -5 & 2\end{bmatrix}$ (iv) $\begin{bmatrix}1 & 5 \\ -1 & 2\end{bmatrix}$

Choose the correct answer in the Exercises 11 and 12.

Solution

(i) Let $A= \begin{bmatrix} 3 & 5 \\ 1 & -1\end{bmatrix} $, then $A^{\prime}= \begin{bmatrix} 3 & 1 \\ 5 & -1 \end{bmatrix} $

$ \begin{aligned} & \text{ Now, } A+A^{\prime}= \begin{bmatrix} 3 & 5 \\ 1 & -1 \end{bmatrix} + \begin{bmatrix} 3 & 1 \\ 5 & -1 \end{bmatrix} = \begin{bmatrix} 6 & 6 \\ 6 & -2 \end{bmatrix} \\ & \text{ Let } P=\frac{1}{2}(A+A^{\prime})=\frac{1}{2} \begin{bmatrix} 6 & 6 \\ 6 & -2 \end{bmatrix} = \begin{bmatrix} 3 & 3 \\ 3 & -1 \end{bmatrix} \\ & \text{ Now, } P^{\prime}= \begin{bmatrix} 3 & 3 \\ 3 & -1 \end{bmatrix} =P \end{aligned} $

Thus, $P=\frac{1}{2}(A+A^{\prime})$ is a symmetric matrix.

Now, $A-A^{\prime}= \begin{bmatrix} 3 & 5 \\ 1 & -1\end{bmatrix} - \begin{bmatrix} 3 & 1 \\ 5 & -1\end{bmatrix} = \begin{bmatrix} 0 & 4 \\ -4 & 0 \end{bmatrix} $

Let $Q=\frac{1}{2}(A-A^{\prime})=\frac{1}{2} \begin{bmatrix} 0 & 4 \\ -4 & 0\end{bmatrix} = \begin{bmatrix} 0 & 2 \\ -2 & 0 \end{bmatrix} $

Now, $Q^{\prime}= \begin{bmatrix} 0 & 2 \\ -2 & 0 \end{bmatrix} =-Q$

Thus, $Q=\frac{1}{2}(A-A^{\prime})$ is a skew-symmetric matrix.

Representing $A$ as the sum of $P$ and $Q$ :

$P+Q= \begin{bmatrix} 3 & 3 \\ 3 & -1\end{bmatrix} + \begin{bmatrix} 0 & 2 \\ -2 & 0\end{bmatrix} = \begin{bmatrix} 3 & 5 \\ 1 & -1 \end{bmatrix} =A$

(ii) Let $A= \begin{bmatrix} 6 & -2 & 2 \\ -2 & 3 & -1 \\ 2 & -1 & 3\end{bmatrix} $, then $A^{\prime}= \begin{bmatrix} 6 & -2 & 2 \\ -2 & 3 & -1 \\ 2 & -1 & 3 \end{bmatrix} $

Now, $A+A^{\prime}= \begin{bmatrix} 6 & -2 & 2 \\ -2 & 3 & -1 \\ 2 & -1 & 3\end{bmatrix} + \begin{bmatrix} 6 & -2 & 2 \\ -2 & 3 & -1 \\ 2 & -1 & 3\end{bmatrix} = \begin{bmatrix} 12 & -4 & 4 \\ -4 & 6 & -2 \\ 4 & -2 & 6 \end{bmatrix} $

Let $P=\frac{1}{2}(A+A^{\prime})=\frac{1}{2} \begin{bmatrix} 12 & -4 & 4 \\ -4 & 6 & -2 \\ 4 & -2 & 6\end{bmatrix} = \begin{bmatrix} 6 & -2 & 2 \\ -2 & 3 & -1 \\ 2 & -1 & 3 \end{bmatrix} $

Now, $P^{\prime}= \begin{bmatrix} 6 & -2 & 2 \\ -2 & 3 & -1 \\ 2 & -1 & 3 \end{bmatrix} =P$

Thus, $P=\frac{1}{2}(A+A^{\prime})$ is a symmetric matrix.

Now, $A-A^{\prime}= \begin{bmatrix} 6 & -2 & 2 \\ -2 & 3 & -1 \\ 2 & -1 & 3\end{bmatrix} + \begin{bmatrix} 6 & -2 & 2 \\ -2 & 3 & -1 \\ 2 & -1 & 3\end{bmatrix} = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} $

Let $Q=\frac{1}{2}(A-A^{\prime})= \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} $

Now, $Q^{\prime}= \begin{cases} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{cases} =-Q$

Thus, $Q=\frac{1}{2}(A-A^{\prime})$ is a skew-symmetric matrix.

Representing $A$ as the sum of $P$ and $Q$ :

$P+Q= \begin{bmatrix} 6 & -2 & 2 \\ -2 & 3 & -1 \\ 2 & -1 & 3\end{bmatrix} + \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0\end{bmatrix} = \begin{bmatrix} 6 & -2 & 2 \\ -2 & 3 & -1 \\ 2 & -1 & 3 \end{bmatrix} =A$

(iii) Let $A= \begin{bmatrix} 3 & 3 & -1 \\ -2 & -2 & 1 \\ -4 & -5 & 2\end{bmatrix} $, then $A^{\prime}= \begin{bmatrix} 3 & -2 & -4 \\ 3 & -2 & -5 \\ -1 & 1 & 2 \end{bmatrix} $

Now, $A+A^{\prime}= \begin{bmatrix} 3 & 3 & -1 \\ -2 & -2 & 1 \\ -4 & -5 & 2\end{bmatrix} + \begin{bmatrix} 3 & -2 & -4 \\ 3 & -2 & -5 \\ -1 & 1 & 2\end{bmatrix} = \begin{bmatrix} 6 & 1 & -5 \\ 1 & -4 & -4 \\ -5 & -4 & 4 \end{bmatrix} $

Let $P=\frac{1}{2}(A+A^{\prime})=\frac{1}{2} \begin{bmatrix} 6 & 1 & -5 \\ 1 & -4 & -4 \\ -5 & -4 & 4\end{bmatrix} = \begin{bmatrix} 3 & \frac{1}{2} & -\frac{5}{2} \\ \frac{1}{2} & -2 & -2 \\ -\frac{5}{2} & -2 & 2 \end{bmatrix} $

Now, $P^{\prime}= \begin{bmatrix} 3 & \frac{1}{2} & -\frac{5}{2} \\ \frac{1}{2} & -2 & -2 \\ -\frac{5}{2} & -2 & 2 \end{bmatrix} =P$

Thus, $P=\frac{1}{2}(A+A^{\prime})$ is a symmetric matrix.

Now, $A-A^{\prime}= \begin{bmatrix} 3 & 3 & -1 \\ -2 & -2 & 1 \\ -4 & -5 & 2\end{bmatrix} - \begin{bmatrix} 3 & -2 & -4 \\ 3 & -2 & -5 \\ -1 & 1 & 2\end{bmatrix} = \begin{bmatrix} 0 & 5 & 3 \\ -5 & 0 & 6 \\ -3 & -6 & 0 \end{bmatrix} $

Let $Q=\frac{1}{2}(A-A^{\prime})=\frac{1}{2} \begin{bmatrix} 0 & 5 & 3 \\ -5 & 0 & 6 \\ -3 & -6 & 0\end{bmatrix} = \begin{bmatrix} 0 & \frac{5}{2} & \frac{3}{2} \\ -\frac{5}{2} & 0 & 3 \\ -\frac{3}{2} & -3 & 0 \end{bmatrix} $

Now, $Q^{\prime}= \begin{bmatrix} 0 & -\frac{5}{2} & -\frac{3}{2} \\ \frac{5}{2} & 0 & -3 \\ \frac{3}{2} & 3 & 0 \end{bmatrix} =-Q$

Thus, $Q=\frac{1}{2}(A-A^{\prime})$ is a skew-symmetric matrix.

Representing $A$ as the sum of $P$ and $Q$ :

$P+Q= \begin{bmatrix} 3 & \frac{1}{2} & -\frac{5}{2} \\ \frac{1}{2} & -2 & -2 \\ -\frac{5}{2} & -2 & 2\end{bmatrix} + \begin{bmatrix} 0 & \frac{5}{2} & \frac{3}{2} \\ -\frac{5}{2} & 0 & 3 \\ -\frac{3}{2} & -3 & 0\end{bmatrix} = \begin{bmatrix} 3 & 3 & -1 \\ -2 & -2 & 1 \\ -4 & -5 & 2 \end{bmatrix} =A$

(iv) Let $A= \begin{bmatrix} 1 & 5 \\ -1 & 2\end{bmatrix} $, then $A^{\prime}= \begin{bmatrix} 1 & -1 \\ 5 & 2 \end{bmatrix} $

Now $A+A^{\prime}= \begin{bmatrix} 1 & 5 \\ -1 & 2\end{bmatrix} + \begin{bmatrix} 1 & -1 \\ 5 & 2\end{bmatrix} = \begin{bmatrix} 2 & 4 \\ 4 & 4 \end{bmatrix} $

Let $P=\frac{1}{2}(A+A^{\prime})= \begin{cases} 1 & 2 \\ 2 & 2 \end{cases} $

Now, $P^{\prime}= \begin{bmatrix} 1 & 2 \\ 2 & 2 \end{bmatrix} =P$

Thus, $P=\frac{1}{2}(A+A^{\prime})$ is a symmetric matrix.

Now, $A-A^{\prime}= \begin{bmatrix} 1 & 5 \\ -1 & 2\end{bmatrix} - \begin{bmatrix} 1 & -1 \\ 5 & 2\end{bmatrix} = \begin{bmatrix} 0 & 6 \\ -6 & 0 \end{bmatrix} $

Let $Q=\frac{1}{2}(A-A^{\prime})= \begin{bmatrix} 0 & 3 \\ -3 & 0 \end{bmatrix} $

Now, $Q^{\prime}= \begin{bmatrix} 0 & -3 \\ 3 & 0 \end{bmatrix} =-Q$

Thus, $Q=\frac{1}{2}(A-A^{\prime})$ is a skew-symmetric matrix.

Representing $A$ as the sum of $P$ and $Q$ :

$ P+Q= \begin{bmatrix} 1 & 2 \\ 2 & 2 \end{bmatrix} + \begin{bmatrix} 0 & 3 \\ -3 & 0 \end{bmatrix} = \begin{bmatrix} 1 & 5 \\ -1 & 2 \end{bmatrix} =A $

11. If $A, B$ are symmetric matrices of same order, then $A B-B A$ is a

(A) Skew symmetric matrix

(B) Symmetric matrix

(C) Zero matrix

(D) Identity matrix

Solution

The correct answer is A.

$A$ and $B$ are symmetric matrices, therefore, we have:

$$ \begin{equation*} A^{\prime}=A \text{ and } B^{\prime}=B \tag{1} \end{equation*} $$

$$ \begin{matrix} \text{ Consider }(A B-B A)^{\prime} & =(A B)^{\prime}-(B A)^{\prime} & & {[(A-B)^{\prime}=A^{\prime}-B^{\prime}]} \\ & =B^{\prime} A^{\prime}-A^{\prime} B^{\prime} & & {[(A B)^{\prime}=B^{\prime} A^{\prime}]} \\ & =B A-A B & {[\text{ by (1)] }} \tag{1}\\ & =-(A B-B A) & \end{matrix} $$

$\therefore(A B-B A)^{\prime}=-(A B-B A)$

Thus, $(A B-B A)$ is a skew-symmetric matrix.

12. If $A=\begin{bmatrix}\cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha\end{bmatrix}$, and $A+A^{\prime}=I$, then the value of $\alpha$ is (A) $\frac{\pi}{6}$ (B) $\frac{\pi}{3}$ (C) $\pi$ (D) $\frac{3 \pi}{2}$

Solution

The correct answer is $B$.

$ \begin{aligned} & A= \begin{bmatrix} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{bmatrix} \\ & \Rightarrow A^{\prime}= \begin{bmatrix} \cos \alpha & \sin \alpha \\ -\sin \alpha & \cos \alpha \end{bmatrix} \end{aligned} $

Now, $A+A^{\prime}=I$

$ \begin{aligned} & \therefore \begin{bmatrix} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{bmatrix} + \begin{bmatrix} \cos \alpha & \sin \alpha \\ -\sin \alpha & \cos \alpha \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \\ & \Rightarrow \begin{bmatrix} 2 \cos \alpha & 0 \\ 0 & 2 \cos \alpha \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \end{aligned} $

Comparing the corresponding elements of the two matrices, we have:

$ \begin{aligned} & 2 \cos \alpha=1 \\ & \Rightarrow \cos \alpha=\frac{1 \pi}{2}=\cos \frac{\pi}{3} \\ & \therefore \alpha=\frac{\pi}{3} \end{aligned} $

Invertible Matrices

Definition 6 If $A$ is a square matrix of order $m$, and if there exists another square matrix $B$ of the same order $m$, such that $AB=BA=I$, then $B$ is called the inverse matrix of $A$ and it is denoted by $A^{-1}$. In that case $A$ is said to be invertible.

For example, let $A=\begin{bmatrix}2 & 3 \\ 1 & 2\end{bmatrix}$ and $B=\begin{bmatrix}2 & -3 \\ -1 & 2\end{bmatrix}$ be two matrices.

Now

$$\begin{aligned} AB & =\begin{bmatrix} 2 & 3 \\ 1 & 2 \end{bmatrix}\begin{bmatrix} 2 & -3 \\ -1 & 2 \end{bmatrix} \\ & =\begin{bmatrix} 4-3 & -6+6 \\ 2-2 & -3+4 \end{bmatrix}=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}=I \end{aligned} $$

Also $BA=\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix}=I$. Thus $B$ is the inverse of $A$, in other words $B=A^{-1}$ and $A$ is inverse of $B$, i.e., $A=B^{-1}$

$\sigma$ Note

1. A rectangular matrix does not possess inverse matrix, since for products $B A$ and $AB$ to be defined and to be equal, it is necessary that matrices $A$ and $B$ should be square matrices of the same order.

2. If $B$ is the inverse of $A$, then $A$ is also the inverse of $B$.

Theorem 3 (Uniqueness of inverse) Inverse of a square matrix, if it exists, is unique. Proof Let $A=[a_{i j}]$ be a square matrix of order $m$. If possible, let $B$ and $C$ be two inverses of $A$. We shall show that $B=C$.

Since B is the inverse of A

$$ AB=BA=I $$

Since $C$ is also the inverse of $A$

$$ AC=CA=I $$

Thus

$$ B=BI=B(AC)=(BA) C=IC=C $$

Theorem 4 If $A$ and $B$ are invertible matrices of the same order, then $(A B)^{-1}=B^{-1} A^{-1}$. Proof From the definition of inverse of a matrix, we have

or

$$ (AB)(AB)^{-1}=1 $$

or

$$ A^{-1}(AB)(AB)^{-1}=A^{-1} I \bigcirc(\text { Pre multiplying both sides by } A^{-1}) $$

$(A^{-1} A) B(A B)^{-1}=A^{-1} \quad(.$ Since $.A^{-1} I=A^{-1})$

or IB $(A B)^{-1}=A^{-1}$

or

$B(AB)^{-1}=A^{-1}$

or

$$ B^{-1} B(AB)^{-1}=B^{-1} A^{-1} $$

or

$I(AB)^{-1}=B^{-1} A^{-1}$

Hence $(AB)^{-1}=B^{-1} A^{-1}$

EXERCISE 3.4

1. Matrices $A$ and $B$ will be inverse of each other only if

(A) $AB=BA$ (B) $AB=BA=0$

(C) $AB=0, BA=I$ (D) $AB=BA=I$

Solution

We know that if $A$ is a square matrix of order $m$, and if there exists another square matrix $B$ of the same order $m$, such that $A B=B A=I$, then $B$ is said to be the inverse of $A$. In this case, it is clear that $A$ is the inverse of $B$.

Thus, matrices $A$ and $B$ will be inverses of each other only if $A B=B A=I$.

Miscellaneous Examples

Example 23 If $A=\begin{bmatrix}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta\end{bmatrix}$, then prove that $A^{n}=\begin{bmatrix}\cos n \theta & \sin n \theta \\ -\sin n \theta & \cos n \theta\end{bmatrix}, n \in \mathbf{N}$.

Solution We shall prove the result by using principle of mathematical induction.

We have

$$\begin{aligned} & P(n): \text { If } A=\begin{bmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{bmatrix} \text {, then } A^{n}=\begin{bmatrix} \cos n \theta & \sin n \theta \\ -\sin n \theta & \cos n \theta \end{bmatrix}, n \in \mathbf{N} \\ & P(1): A=\begin{bmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{bmatrix} \text {, so } A^{1}=\begin{bmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{bmatrix} \end{aligned} $$

Therefore, $\quad$ the result is true for $n=1$.

Let the result be true for $n=k$. So

$$ P(k): A=\begin{bmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{bmatrix} \text {, then } A^{k}=\begin{bmatrix} \cos k \theta & \sin k \theta \\ -\sin k \theta & \cos k \theta \end{bmatrix} $$

Now, we prove that the result holds for $n=k+1$

Now

$$\begin{aligned} A^{k+1} & =A \cdot A^{k}=\begin{bmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{bmatrix}\begin{bmatrix} \cos k \theta & \sin k \theta \\ -\sin k \theta & \cos k \theta \end{bmatrix} \\ & =\begin{bmatrix} \cos \theta \cos k \theta-\sin \theta \sin k \theta & \cos \theta \sin k \theta+\sin \theta \cos k \theta \\ -\sin \theta \cos k \theta+\cos \theta \sin k \theta & -\sin \theta \sin k \theta+\cos \theta \cos k \theta \end{bmatrix} \\ & =\begin{bmatrix} \cos (\theta+k \theta) & \sin (\theta+k \theta) \\ -\sin (\theta+k \theta) & \cos (\theta+k \theta) \end{bmatrix}=\begin{bmatrix} \cos (k+1) \theta & \sin (k+1) \theta \\ -\sin (k+1) \theta & \cos (k+1) \theta \end{bmatrix} \end{aligned} $$

Therefore, the result is true for $n=k+1$. Thus by principle of mathematical induction, we have $A^{n}=\begin{bmatrix}\cos n \theta & \sin n \theta \\ -\sin n \theta & \cos n \theta\end{bmatrix}$, holds for all natural numbers.

Example 24 If $A$ and $B$ are symmetric matrices of the same order, then show that $A B$ is symmetric if and only if $A$ and $B$ commute, that is $AB=BA$.

Solution Since A and B are both symmetric matrices, therefore $A^{\prime}=A$ and $B^{\prime}=B$.

Let $\quad AB$ be symmetric, then $(AB)^{\prime}=AB$

But

$$\begin{aligned} (AB)^{\prime} & =B^{\prime} A^{\prime}=BA(\text { Why? }) \\ BA & =AB \end{aligned} $$

Therefore

Conversely, if $AB=BA$, then we shall show that $AB$ is symmetric.

Now

$$\begin{aligned} (AB)^{\prime} & =B^{\prime} A^{\prime} \\ & =B A(\text { as } A \text { and } B \text { are symmetric}) \\ & =AB \end{aligned} $$

Hence $AB$ is symmetric.

Example 25 Let $A=\begin{bmatrix}2 & -1 \\ 3 & 4\end{bmatrix}, B=\begin{bmatrix}5 & 2 \\ 7 & 4\end{bmatrix}, C=\begin{bmatrix}2 & 5 \\ 3 & 8\end{bmatrix}$. Find a matrix $D$ such that $CD-AB=O$.

Solution Since A, B, C are all square matrices of order 2, and CD - AB is well defined, $D$ must be a square matrix of order 2.

Let

$$\begin{aligned} & D=\begin{bmatrix} a & b \\ c & d \end{bmatrix} . \text { Then } CD-AB=0 \text { gives } \\ & {\begin{bmatrix} 2 & 5 \\ 3 & 8 \end{bmatrix}\begin{bmatrix} a & b \\ c & d \end{bmatrix}-\begin{bmatrix} 2 & -1 \\ 3 & 4 \end{bmatrix}\begin{bmatrix} 5 & 2 \\ 7 & 4 \end{bmatrix}=O} \\ & {\begin{bmatrix} 2 a+5 c & 2 b+5 d \\ 3 a+8 c & 3 b+8 d \end{bmatrix}-\begin{bmatrix} 3 & 0 \\ 43 & 22 \end{bmatrix}=\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}} \\ & {\begin{bmatrix} 2 a+5 c-3 & 2 b+5 d \\ 3 a+8 c-43 & 3 b+8 d-22 \end{bmatrix}=\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}} \end{aligned} $$

or

By equality of matrices, we get

$$\begin{bmatrix} 2 a+5 c-3=0 \\ 3 a+8 c-43=0 \\ 2 b+5 d=0 \\ 3 b+8 d-22=0 \end{bmatrix} $$

and

Solving (1) and (2), we get $a=-191, c=77$. Solving (3) and (4), we get $b=-110$, $d=44$.

Therefore

$$ D=\begin{bmatrix} a & b \\ c & d \end{bmatrix}=\begin{bmatrix} -191 & -110 \\ 77 & 44 \end{bmatrix} $$

Miscellaneous Exercise on Chapter 3

1. If $A$ and $B$ are symmetric matrices, prove that $AB-BA$ is a skew symmetric matrix.

Solution

It is given that $A$ and $B$ are symmetric matrices. Therefore, we have:

$$ \begin{equation*} A^{\prime}=A \text{ and } B^{\prime}=B \tag{1} \end{equation*} $$

Now, $(A B-B A)^{\prime}=(A B)^{\prime}-(B A)^{\prime}$

$[(A-B)^{\prime}=A^{\prime}-B^{\prime}]$

$=B^{\prime} A^{\prime}-A^{\prime} B^{\prime}$

$[(A B)^{\prime}=B^{\prime} A^{\prime}]$

$=B A-A B$

[Using (1)]

$=-(A B-B A)$

$\therefore(A B-B A)^{\prime}=-(A B-B A)$

Thus, $(A B-B A)$ is a skew-symmetric matrix.

2. Show that the matrix $B^{\prime} A B$ is symmetric or skew symmetric according as $A$ is symmetric or skew symmetric.

Solution

We suppose that $A$ is a symmetric matrix, then $A^{\prime}=A$

Consider

$ \begin{matrix} (B^{\prime} A B)^{\prime} & ={B^{\prime}(A B)}^{\prime} & \\ & =(A B)^{\prime}(B^{\prime})^{\prime} & {[(A B)^{\prime}=B^{\prime} A^{\prime}]} \\ & =B^{\prime} A^{\prime}(B) & {[(B^{\prime})^{\prime}=B]} \\ & =B^{\prime}(A^{\prime} B) & \\ & =B^{\prime}(A B) & \end{matrix} $

Thus, if $A$ is a symmetric matrix, then $B^{\prime} A B$ is a symmetric matrix.

Now, we suppose that $A$ is a skew-symmetric matrix.

Then, $A^{\prime}=-A$

Consider

$ \begin{aligned} & (B^{\prime} A B)^{\prime}=[B^{\prime}(A B)]^{\prime}=(A B)^{\prime}(B^{\prime})^{\prime} \\ & =(B^{\prime} A^{\prime}) B=B^{\prime}(-A) B \\ & =-B^{\prime} A B \\ & \therefore(B^{\prime} A B)^{\prime}=-B^{\prime} A B \end{aligned} $

Thus, if $A$ is a skew-symmetric matrix, then $B^{\prime} A B$ is a skew-symmetric matrix.

Hence, if $A$ is a symmetric or skew-symmetric matrix, then $B^{\prime} A B$ is a symmetric or skewsymmetric matrix accordingly.

3. Find the values of $x, y, z$ if the matrix $A=\begin{bmatrix}0 & 2 y & z \\ x & y & -z \\ x & -y & z\end{bmatrix}$ satisfy the equation $A^{\prime} A=I$.

Solution

Given,

$A=\begin{bmatrix}0 & 2 y & z \\ x & y & -z \\ x & -y & z\end{bmatrix}$

$A=\begin{bmatrix}0 & x & x \\ 2y & y & -y \\ z & -z & z\end{bmatrix}$

$A=\begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}$

Now,A’A=I

Putting values

$\left[\begin{array}{ccc} 0 & x & x \\ 2 y & y & -y \\ z & -z & z \end{array}\right]\left[\begin{array}{ccc} 0 & 2 y & z \\ x & y & -z \\ x & -y & z \end{array}\right]\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array}\right]$

$\left[\begin{array}{ccc} o(0)+x(x)+x(x) & o(2 y)+x(y)+x(-y) & o(z)+x(-z)+x(z) \\ 2 y(0)+y(x)-y(x) & 2 y(2 y)+y(y)-y(-y) & 2 y(z)+y(-z)-y(z) \\ z(0)-z(x)+z(x) & z(2 y)-z(y)+z(-y) & z(z)-z(-z)+z(z) \end{array}\right]=\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array}\right]$

$\left[\begin{array}{ccc} 0+x^2+x^2 & 0+x y-x y & 0-x z+x z \\ 0+x y-x y & 4 y^2+y^2+y^2 & 2 z y-z y-z y \\ 0-x z+x z & 2 z y-z y-z y & z^2+z^2+z^2 \end{array}\right]=\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array}\right]$

$\left[\begin{array}{ccc} 2 x^2 & 0 & 0 \\ 0 & 6 y^2 & 0 \\ 0 & 0 & 3 z^2 \end{array}\right]=\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array}\right]$

Since matrices are equal, corresponding elements are equal, $$ \begin{aligned} & 2 \mathrm{x}^2=1 \\ & \mathrm{x}^2=\frac{1}{2} \\ & \mathrm{x}= \pm \sqrt{\frac{1}{2}} \\ & \mathrm{x}= \pm \frac{1}{\sqrt{2}} \end{aligned} $$

$$ \begin{aligned} & 6 y^2=1 \\ & y^2=\frac{1}{6} \\ & y= \pm \sqrt{\frac{1}{6}} \\ & y= \pm \frac{1}{\sqrt{6}} \\ \end{aligned} $$

$$ \begin{aligned} & 3 \mathrm{z}^2=1 \\ & \mathrm{z}^2=\frac{1}{3} \\ & \mathrm{z}= \pm \sqrt{\frac{1}{3}} \\ & \mathrm{z}= \pm \frac{1}{\sqrt{3}} \ \end{aligned} $$

Thus, $\mathrm{x}= \pm \frac{1}{\sqrt{2}}, \mathrm{y}= \pm \frac{1}{\sqrt{6}}, \mathrm{z}= \pm \frac{1}{\sqrt{3}}$

4. For what values of $x:\begin{bmatrix}1 & 2 & 1\end{bmatrix}\begin{bmatrix}1 & 2 & 0 \\ 2 & 0 & 1 \\ 1 & 0 & 2\end{bmatrix}\begin{bmatrix}{l}0 \\ 2 \\ x\end{bmatrix}=O$ ?

Solution

We have:

$ \begin{aligned} & { \begin{bmatrix} 1 & 2 & 1 \end{bmatrix} \begin{bmatrix} 1 & 2 & 0 \\ 2 & 0 & 1 \\ 1 & 0 & 2 \end{bmatrix} \begin{bmatrix} 0 \\ 2 \\ x \end{bmatrix} =0} \\ & \Rightarrow \begin{bmatrix} 1+4+1 & 2+0+0 & 0+2+2 \end{bmatrix} \begin{bmatrix} 0 \\ 2 \\ x \end{bmatrix} =0 \\ & \Rightarrow \begin{bmatrix} 6 & 2 & 4 \end{bmatrix} \begin{bmatrix} 0 \\ 2 \\ x \end{bmatrix} =0 \\ & \Rightarrow[6(0)+2(2)+4(x)]=0 \\ & \Rightarrow[4+4 x]=[0] \\ & \therefore 4+4 x=0 \\ & \Rightarrow x=-1 \end{aligned} $

Thus, the required value of $x$ is -1 .

5. If $A=\begin{bmatrix}3 & 1 \\ -1 & 2\end{bmatrix}$, show that $A^{2}-5 A+7 I=0$.

Solution

It is given that $A= \begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix} $

$ \begin{aligned} \therefore A^{2}=A \cdot A & = \begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix} \begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix} \\ & = \begin{bmatrix} 3(3)+1(-1) & 3(1)+1(2) \\ -1(3)+2(-1) & -1(1)+2(2) \end{bmatrix} \\ & = \begin{bmatrix} 9-1 & 3+2 \\ -3-2 & -1+4 \end{bmatrix} = \begin{bmatrix} 8 & 5 \\ -5 & 3 \end{bmatrix} \end{aligned} $

$\therefore$ L.H.S. $=A^{2}-5 A+7 I$

$= \begin{bmatrix} 8 & 5 \\ -5 & 3\end{bmatrix} -5 \begin{bmatrix} 3 & 1 \\ -1 & 2\end{bmatrix} +7 \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} $

$= \begin{bmatrix} 8 & 5 \\ -5 & 3\end{bmatrix} - \begin{bmatrix} 15 & 5 \\ -5 & 10\end{bmatrix} + \begin{bmatrix} 7 & 0 \\ 0 & 7 \end{bmatrix} $

$= \begin{bmatrix} -7 & 0 \\ 0 & -7\end{bmatrix} + \begin{bmatrix} 7 & 0 \\ 0 & 7 \end{bmatrix} $

$= \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} $

$=O=$ R.H.S.

$\therefore A^{2}-5 A+7 I=O$

6. Find $x$, if $\begin{bmatrix}x & -5 & -1\end{bmatrix}\begin{bmatrix}1 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 0 & 3\end{bmatrix}\begin{bmatrix}{l}x \\ 4 \\ 1\end{bmatrix}=O$

Solution

We have:

$ \begin{aligned} & { \begin{bmatrix} x & -5 & -1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 0 & 3 \end{bmatrix} \begin{bmatrix} x \\ 4 \\ 1 \end{bmatrix} =O} \\ & \Rightarrow \begin{bmatrix} x+0-2 & 0-10+0 & 2 x-5-3] \end{bmatrix} \begin{bmatrix} x \\ 4 \\ 1 \end{bmatrix} =O \\ & \Rightarrow \begin{bmatrix} x-2 & -10 & 2 x-8 \end{bmatrix} \begin{bmatrix} x \\ 4 \\ 1 \end{bmatrix} =O \\ & \Rightarrow[x(x-2)-40+2 x-8]=O \\ & \Rightarrow[x^{2}-2 x-40+2 x-8]=[0] \\ & \Rightarrow[x^{2}-48]=[0] \\ & \therefore x^{2}-48=0 \\ & \Rightarrow x^{2}=48 \\ & \Rightarrow x= \pm 4 \sqrt{3} \end{aligned} $

7. A manufacturer produces three products $x, y, z$ which he sells in two markets. Annual sales are indicated below:

Market	Products
I	$ 10,000 \hspace{5mm} 2,000 \hspace{5mm} 18,000 $
II	$ 6,000 \hspace{5mm} 20,000\hspace{5mm} 8,000$

(a) If unit sale prices of $x, y$ and $z$ are ₹ 2.50 , ₹ 1.50 and ₹ 1.00 , respectively, find the total revenue in each market with the help of matrix algebra.

(b) If the unit costs of the above three commodities are ₹ 2.00 , ₹ 1.00 and 50 paise respectively. Find the gross profit.

Solution

(a) The unit sale prices of $x, y$, and $z$ are respectively given as $Rs 2.50$, Rs 1.50, and Rs 1.00 .

Consequently, the total revenue in market $\mathbf{I}$ can be represented in the form of a matrix as:

$ \begin{bmatrix} 10000 & 2000 & 18000\end{bmatrix} \begin{bmatrix} 2.50 \\ 1.50 \\ 1.00 \end{bmatrix} $

$=10000 \times 2.50+2000 \times 1.50+18000 \times 1.00$

$=25000+3000+18000$

$=46000$

The total revenue in market II can be represented in the form of a matrix as:

$ \begin{aligned} & { \begin{bmatrix} 6000 & 20000 & 8000 \end{bmatrix} \begin{bmatrix} 2.50 \\ 1.50 \\ 1.00 \end{bmatrix} } \\ & =6000 \times 2.50+20000 \times 1.50+8000 \times 1.00 \\ & =15000+30000+8000 \\ & =53000 \end{aligned} $

Therefore, the total revenue in market $\mathbf{I}$ isRs 46000 and the same in market II isRs 53000.

(b) The unit cost prices of $x, y$, and $z$ are respectively given as $Rs 2.00, Rs 1.00$, and 50 paise.

Consequently, the total cost prices of all the products in market $\mathbf{I}$ can be represented in the form of a matrix as:

$ \begin{aligned} & { \begin{bmatrix} 10000 & 2000 & 18000 \end{bmatrix} \begin{bmatrix} 2.00 \\ 1.00 \\ 0.50 \end{bmatrix} } \\ & =10000 \times 2.00+2000 \times 1.00+18000 \times 0.50 \\ & =20000+2000+9000 \\ & =31000 \end{aligned} $

Since the total revenue in market $\mathbf{I}$ isRs 46000 , the gross profit in this marketis (Rs 46000 - Rs 31000) Rs 15000.

The total cost prices of all the products in market II can be represented in the form of a matrix as:

$ \begin{aligned} & { \begin{bmatrix} 6000 & 20000 & 8000 \end{bmatrix} \begin{bmatrix} 2.00 \\ 1.00 \\ 0.50 \end{bmatrix} } \\ & =6000 \times 2.00+20000 \times 1.00+8000 \times 0.50 \\ & =12000+20000+4000 \\ & =\text{ Rs } 36000 \end{aligned} $

Since the total revenue in market II isRs 53000, the gross profit in this market is (Rs 53000 - Rs 36000) Rs 17000.

8. Find the matrix $X$ so that $X\begin{bmatrix}1 & 2 & 3 \\ 4 & 5 & 6\end{bmatrix}=\begin{bmatrix}-7 & -8 & -9 \\ 2 & 4 & 6\end{bmatrix}$

Choose the correct answer in the following questions:

Solution

It is given that:

$ X \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} = \begin{bmatrix} -7 & -8 & -9 \\ 2 & 4 & 6 \end{bmatrix} $

The matrix given on the R.H.S. of the equation is a $2 \times 3$ matrix and the one given on the L.H.S. of the equation is a $2 \times 3$ matrix. Therefore, $X$ has to be a $2 \times 2$ matrix.

Now, let $X= \begin{cases} a & c \\ b & d \end{cases} $

Therefore, we have:

$ \begin{aligned} & { \begin{bmatrix} a & c \\ b & d \end{bmatrix} \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} = \begin{bmatrix} -7 & -8 & -9 \\ 2 & 4 & 6 \end{bmatrix} } \\ & \Rightarrow \begin{bmatrix} a+4 c & 2 a+5 c & 3 a+6 c \\ b+4 d & 2 b+5 d & 3 b+6 d \end{bmatrix} = \begin{bmatrix} -7 & -8 & -9 \\ 2 & 4 & 6 \end{bmatrix} \end{aligned} $

Equating the corresponding elements of the two matrices, we have:

$ \begin{matrix} a+4 c=-7, & 2 a+5 c=-8, & 3 a+6 c=-9 \\ b+4 d=2, & 2 b+5 d=4, & 3 b+6 d=6 \end{matrix} $

Now, $a+4 c=-7 \Rightarrow a=-7-4 c$

$ \begin{aligned} \therefore 2 a+5 c=-8 & \Rightarrow-14-8 c+5 c=-8 \\ & \Rightarrow-3 c=6 \\ & \Rightarrow c=-2 \end{aligned} $

$\therefore a=-7-4(-2)=-7+8=1$

Now, $b+4 d=2 \Rightarrow b=2-4 d$

$ \begin{aligned} \therefore 2 b+5 d=4 & \Rightarrow 4-8 d+5 d=4 \\ & \Rightarrow-3 d=0 \\ & \Rightarrow d=0 \end{aligned} $

$\therefore b=2-4(0)=2$

Thus, $a=1, b=2, c=-2, d=0$

Hence, the required matrix $X$ is $ \begin{cases} 1 & -2 \\ 2 & 0 \end{cases} $.

9. If $A=\begin{bmatrix}\alpha & \beta \\ \gamma & -\alpha\end{bmatrix}$ is such that $A^{2}=I$, then

(A) $1+\alpha^{2}+\beta \gamma=0$

(B) $1-\alpha^{2}+\beta \gamma=0$

(C) $1-\alpha^{2}-\beta \gamma=0$

(D) $1+\alpha^{2}-\beta \gamma=0$

Solution

$ \begin{aligned} & A= \begin{bmatrix} \alpha & \beta \\ \gamma & -\alpha \end{bmatrix} \\ & \therefore A^{2}=A \cdot A= \begin{bmatrix} \alpha & \beta \\ \gamma & -\alpha \end{bmatrix} \begin{bmatrix} \alpha & \beta \\ \gamma & -\alpha \end{bmatrix} \\ & = \begin{bmatrix} \alpha^{2}+\beta \gamma & \alpha \beta-\alpha \beta \\ \alpha \gamma-\alpha \gamma & \beta \gamma+\alpha^{2} \end{bmatrix} \\ & = \begin{bmatrix} \alpha^{2}+\beta \gamma & 0 \\ 0 & \beta \gamma+\alpha^{2} \end{bmatrix} \end{aligned} $

Now, $A^{2}=I \Rightarrow \begin{bmatrix} \alpha^{2}+\beta \gamma & 0 \\ 0 & \beta \gamma+\alpha^{2}\end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} $

On comparing the corresponding elements, we have:

$ \begin{aligned} & \alpha^{2}+\beta \gamma=1 \\ & \Rightarrow \alpha^{2}+\beta \gamma-1=0 \\ & \Rightarrow 1-\alpha^{2}-\beta \gamma=0 \end{aligned} $

10. If the matrix $A$ is both symmetric and skew symmetric, then (A) $A$ is a diagonal matrix (B) $A$ is a zero matrix (C) A is a square matrix (D) None of these

Solution

If $A$ is both symmetric and skew-symmetric matrix, then we should have

$ \begin{aligned} & A^{\prime}=A \text{ and } A^{\prime}=-A \\ & \Rightarrow A=-A \\ & \Rightarrow A+A=O \\ & \Rightarrow 2 A=O \\ & \Rightarrow A=O \end{aligned} $

Therefore, $A$ is a zero matrix.

11. If $A$ is square matrix such that $A^{2}=A$, then $(I+A)^{3}-7 A$ is equal to (A) $A$ (B) $I-A$ (C) I (D) $3 A$

Solution

$ \begin{matrix} (I+A)^{3}-7 A & =I^{3}+A^{3}+3 I^{2} A+3 A^{2} I-7 A & \\ & =I+A^{3}+3 A+3 A^{2}-7 A & \\ & =I+A^{2} \cdot A+3 A+3 A-7 A & \\ & =I+A \cdot A-A \\ & =I+A^{2}-A \\ & =I+A-A \\ & =I \\ \therefore(I+A)^{3}-7 & =I \end{matrix} $

Summary

A matrix is an ordered rectangular bmatrix of numbers or functions.

• A matrix having $m$ rows and $n$ columns is called a matrix of order $m \times n$.

• $[a_{i j}]_{m \times 1}$ is a column matrix.

• $[a_{i j}]_{1 \times n}$ is a row matrix.

• An $m \times n$ matrix is a square matrix if $m=n$.

• $A=[a _{i j}] _{m \times m}$ is a diagonal matrix if $a _{i j}=0$, when $i \neq j$.

• $A=[a_{ij}]_{n \times n}$

  is a scalar matrix if $a _ {i j}=0$, when $i \neq j, a _ {ij}=k$, $k$ is some constant, when $i=j$.

• $A=[a_{ij}]_{n \times n}$

  is an identity matrix, if $a_{i j}=1$, when $i=j, a_{i j}=0$, when $i \neq j$.

• A zero matrix has all its elements as zero.

• $A=[a_ {i j}]=[b_ {i j}]=B$ if (i) A and B are of same order, (ii) $a_{i j}=b_{i j}$ for all possible values of $i$ and $j$. $k A=k[a_ {i j}]_ {m \times n}=[k(a_{i j})] _{m \times n}$

$\Delta-A=(-1) A$

$\Delta A-B=A+(-1) B$

$\Delta A+B=B+A$

• $(A+B)+C=A+(B+C)$, where $A, B$ and $C$ are of same order.

$\Delta k(A+B)=k A+k B$, where $A$ and $B$ are of same order, $k$ is constant.

• $ (k+l) A=k A+l A$, where $k$ and $l$ are constant.

• If $A=[a_ {i j}]_ {m \times n}$ and $B=[b_ {j k}]_ {n \times p}$, then $AB=C=[c_ {i k}]_ {m \times p}$, where $c_ {i k}=\sum_ {j=1}^{n} a_ {i j} b_{j k}$

(i) $A(BC)=(AB) C$,

(ii) $A(B+C)=AB+AC$, (iii) $(A+B) C=AC+BC$

$\Delta$ If $A=[a_ {i j}]_ {m \times n}$, then $A^{\prime}$ or $A^{T}=[a_ {j i}]_ {n \times m}$

(i) $(A^{\prime})^{\prime}=A$, (ii) $(k A)^{\prime}=k A^{\prime}$, (iii) $(A+B)^{\prime}=A^{\prime}+B^{\prime}$, (iv) $(AB)^{\prime}=B^{\prime} A^{\prime}$

• $A$ is a symmetric matrix if $A^{\prime}=A$.

$\Delta A$ is a skew symmetric matrix if $A^{\prime}=-A$.

• Any square matrix can be represented as the sum of a symmetric and a skew symmetric matrix.

$\Delta$ If $A$ and $B$ are two square matrices such that $AB=BA=I$, then $B$ is the inverse matrix of $A$ and is denoted by $A^{-1}$ and $A$ is the inverse of $B$.

$\Delta$ Inverse of a square matrix, if it exists, is unique.