RELATIONS AND FUNCTIONS

There is no permanent place in the world for ugly mathematics … . It may be very hard to define mathematical beauty but that is just as true of beauty of any kind, we may not know quite what we mean by a beautiful poem, but that does not prevent us from recognising one when we read it. - G. H. HARDY

Introduction

Recall that the notion of relations and functions, domain, co-domain and range have been introduced in Class XI along with different types of specific real valued functions and their graphs. The concept of the term ‘relation’ in mathematics has been drawn from the meaning of relation in English language, according to which two objects or quantities are related if there is a recognisable connection or link between the two objects or quantities. Let A be the set of students of Class XII of a school and B be the set of students of Class XI of the same school. Then some of the examples of relations from $A$ to $B$ are

(i) $\{(a, b) \in A \times B: \text{a is brother of b}\}$

(ii) $\{(a, b) \in A \times B: \text{a is sister of b}\}$,

Lejeune Dirichlet (1805-1859)

(iii) $\{(a, b) \in A \times B : \text{age of a is greater than age of b}\}$,

(iv) ${(a, b) \in A \times B :}$

${\text{total marks obtained by a in the final examination is less than the total marks obtained by b in the final examination}}$,

(v) $\{(a, b) \in A \times B: a$ lives in the same locality as $b\}$. However, abstracting from this, we define mathematically a relation $R$ from $A$ to $B$ as an arbitrary subset of $A \times B$.

If $(a, b) \in R$, we say that $a$ is related to $b$ under the relation $R$ and we write as $a R b$. In general, $(a, b) \in R$, we do not bother whether there is a recognisable connection or link between $a$ and $b$. As seen in Class XI, functions are special kind of relations.

In this chapter, we will study different types of relations and functions, composition of functions, invertible functions and binary operations.

1.2 Types of Relations

In this section, we would like to study different types of relations. We know that a relation in a set $A$ is a subset of $A \times A$. Thus, the empty set $\phi$ and $A \times A$ are two extreme relations. For illustration, consider a relation $R$ in the set $A=\{1,2,3,4\}$ given by $R=\{(a, b): a-b=10\}$. This is the empty set, as no pair $(a, b)$ satisfies the condition $a-b=10$. Similarly, $R^{\prime}=\{(a, b):|a-b| \geq 0\}$ is the whole set $A \times A$, as all pairs $(a, b)$ in A $\times$ A satisfy $|a-b| \geq 0$. These two extreme examples lead us to the following definitions.

Definition 1 A relation $R$ in a set $A$ is called empty relation, if no element of $A$ is related to any element of $A$, i.e., $R=\phi \subset A \times A$.

Definition 2 A relation $R$ in a set $A$ is called universal relation, if each element of $A$ is related to every element of $A$, i.e., $R=A \times A$.

Both the empty relation and the universal relation are some times called trivial relations.

Example 1 Let $A$ be the set of all students of a boys school. Show that the relation $R$ in $A$ given by $R=\{(a, b): a$ is sister of $b\}$ is the empty relation and $R^{\prime}=\{(a, b):$ the difference between heights of $a$ and $b$ is less than 3 meters $\}$ is the universal relation.

Solution Since the school is boys school, no student of the school can be sister of any student of the school. Hence, $R=\phi$, showing that $R$ is the empty relation. It is also obvious that the difference between heights of any two students of the school has to be less than 3 meters. This shows that $R^{\prime}=A \times A$ is the universal relation.

Remark In Class XI, we have seen two ways of representing a relation, namely raster method and set builder method. However, a relation $R$ in the set $\{1,2,3,4\}$ defined by $R$ $=\{(a, b): b=a+1\}$ is also expressed as $a R b$ if and only if $b=a+1$ by many authors. We may also use this notation, as and when convenient.

If $(a, b) \in R$, we say that $a$ is related to $b$ and we denote it as $a R b$.

One of the most important relation, which plays a significant role in Mathematics, is an equivalence relation. To study equivalence relation, we first consider three types of relations, namely reflexive, symmetric and transitive.

Definition 3 A relation $R$ in a set $A$ is called

(i) reflexive, if $(a, a) \in R$, for every $a \in A$,

(ii) symmetric, if $(a_{1}, a_{2}) \in R$ implies that $(a_{2}, a_{1}) \in R$, for all $a_{1}, a_{2} \in A$.

(iii) transitive, if $(a_{1}, a_{2}) \in R$ and $(a_{2}, a_{3}) \in R$ implies that $(a_{1}, a_{3}) \in R$, for all $a_{1}, a_{2}$, $a_{3} \in A$.

Definition 4 A relation $R$ in a set $A$ is said to be an equivalence relation if $R$ is reflexive, symmetric and transitive.

Example 2 Let $T$ be the set of all triangles in a plane with $R$ a relation in $T$ given by $R=\{(T_{1}, T_{2}): T_{1}.$ is congruent to $.T_{2}\}$. Show that $R$ is an equivalence relation.

Solution $R$ is reflexive, since every triangle is congruent to itself. Further, $(T_{1}, T_{2}) \in R \Rightarrow T_{1}$ is congruent to $T_{2} \Rightarrow T_{2}$ is congruent to $T_{1} \Rightarrow(T_{2}, T_{1}) \in R$. Hence, $R$ is symmetric. Moreover, $(T_{1}, T_{2}),(T_{2}, T_{3}) \in R \Rightarrow T_{1}$ is congruent to $T_{2}$ and $T_{2}$ is congruent to $T_{3} \Rightarrow T_{1}$ is congruent to $T_{3} \Rightarrow(T_{1}, T_{3}) \in R$. Therefore, $R$ is an equivalence relation.

Example 3 $ Let L$ be the set of all lines in a plane and $R$ be the relation in $L$ defined as $R=\{(L_{1}, L_{2}): L_{1}.$ is perpendicular to $.L_{2}\}$. Show that $R$ is symmetric but neither reflexive nor transitive.

Solution $R$ is not reflexive, as a line $L_{1}$ can not be perpendicular to itself, i.e., $(L_{1}, L_{1})$ $\notin R$. R is symmetric as $(L_{1}, L_{2}) \in R$

$$ \begin{array}{ll} \Rightarrow & L_{1} \text { is perpendicular to } L_{2} \\ \Rightarrow & L_{2} \text { is perpendicular to } L_{1} \\ \Rightarrow & (L_{2}, L_{1}) \in R . \end{array} $$

$R$ is not transitive. Indeed, if $L_{1}$ is perpendicular to $L_{2}$ and $L_{2}$ is perpendicular to $L_{3}$, then $L_{1}$ can never be perpendicular to

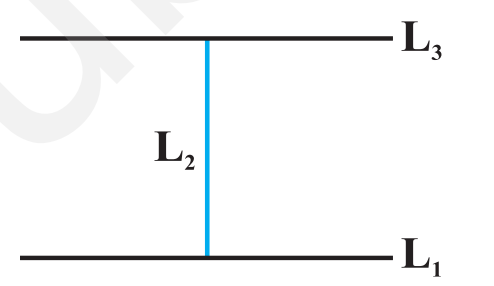
Fig 1.1 $L_{3}$. In fact, $L_{1}$ is parallel to $L_{3}$, i.e., $(L_{1}, L_{2}) \in R,(L_{2}, L_{3}) \in R$ but $(L_{1}, L_{3}) \notin R$.

Example 4 Show that the relation $R$ in the set $\{1,2,3\}$ given by R=\{(1,1),(2,2), (3,3),(1,2),(2,3)\} is reflexive but neither symmetric nor transitive.

Solution $R$ is reflexive, since $(1,1),(2,2)$ and $(3,3)$ lie in $R$. Also, $R$ is not symmetric, as $(1,2) \in R$ but $(2,1) \notin R$. Similarly, $R$ is not transitive, as $(1,2) \in R$ and $(2,3) \in R$ but $(1,3) \notin R$.

Example 5 Show that the relation $R$ in the set $\mathbf{Z}$ of integers given by

$$ R=\{(a, b): 2 \text { divides } a-b\} $$

is an equivalence relation.

Solution $R$ is reflexive, as 2 divides $(a-a)$ for all $a \in \mathbf{Z}$. Further, if $(a, b) \in R$, then 2 divides $a-b$. Therefore, 2 divides $b-a$. Hence, $(b, a) \in R$, which shows that $R$ is symmetric. Similarly, if $(a, b) \in R$ and $(b, c) \in R$, then $a-b$ and $b-c$ are divisible by 2. Now, $a-c=(a-b)+(b-c)$ is even (Why?). So, $(a-c)$ is divisible by 2 . This shows that $R$ is transitive. Thus, $R$ is an equivalence relation in $\mathbf{Z}$.

In Example 5, note that all even integers are related to zero, as $(0, \pm 2),(0, \pm 4)$ etc., lie in $R$ and no odd integer is related to 0 , as $(0, \pm 1),(0, \pm 3)$ etc., do not lie in $R$. Similarly, all odd integers are related to one and no even integer is related to one. Therefore, the set $E$ of all even integers and the set $O$ of all odd integers are subsets of $\mathbf{Z}$ satisfying following conditions:

(i) All elements of $E$ are related to each other and all elements of $O$ are related to each other.

(ii) No element of $E$ is related to any element of $O$ and vice-versa.

(iii) $E$ and $O$ are disjoint and $\mathbf{Z}=E \cup O$.

The subset $E$ is called the equivalence class containing zero and is denoted by [0]. Similarly, $O$ is the equivalence class containing 1 and is denoted by [1]. Note that $[0] \neq[1],[0]=[2 r]$ and $[1]=[2 r+1], r \in \mathbf{Z}$. Infact, what we have seen above is true for an arbitrary equivalence relation $R$ in a set $X$. Given an arbitrary equivalence relation $R$ in an arbitrary set $X, R$ divides $X$ into mutually disjoint subsets $A_{i}$ called partitions or subdivisions of $X$ satisfying:

(i) all elements of $A_{i}$ are related to each other, for all $i$.

(ii) no element of $A_{i}$ is related to any element of $A_{j}, i \neq j$.

(iii) $\cup A_{j}=X$ and $A_{i} \cap A_{j}=\phi, i \neq j$.

The subsets $A_{i}$ are called equivalence classes. The interesting part of the situation is that we can go reverse also. For example, consider a subdivision of the set $\mathbf{Z}$ given by three mutually disjoint subsets $A_{1}, A_{2}$ and $A_{3}$ whose union is $\mathbf{Z}$ with

$$ \begin{aligned} & A_{1}=\{x \in \mathbf{Z}: x \text { is a multiple of } 3\}=\{\ldots,-6,-3,0,3,6, \ldots\} \\ & A_{2}=\{x \in \mathbf{Z}: x-1 \text { is a multiple of } 3\}=\{\ldots,-5,-2,1,4,7, \ldots\} \\ & A_{3}=\{x \in \mathbf{Z}: x-2 \text { is a multiple of } 3\}=\{\ldots,-4,-1,2,5,8, \ldots\} \end{aligned} $$

Define a relation $R$ in $\mathbf{Z}$ given by $R=\{(a, b): 3$ divides $a-b\}$. Following the arguments similar to those used in Example 5, we can show that $R$ is an equivalence relation. Also, $A_{1}$ coincides with the set of all integers in $\mathbf{Z}$ which are related to zero, $A_{2}$ coincides with the set of all integers which are related to 1 and $A_{3}$ coincides with the set of all integers in $\mathbf{Z}$ which are related to 2. Thus, $A_{1}=[0], A_{2}=[1]$ and $A_{3}=[2]$. In fact, $A_{1}=[3 r], A_{2}=[3 r+1]$ and $A_{3}=[3 r+2]$, for all $r \in \mathbf{Z}$.

Example 6 Let $R$ be the relation defined in the set $A=\{1,2,3,4,5,6,7\}$ by R=\{(a, b) : both a and b are either odd or even \}. Show that $R$ is an equivalence relation. Further, show that all the elements of the subset $\{1,3,5,7\}$ are related to each other and all the elements of the subset $\{2,4,6\}$ are related to each other, but no element of the subset $\{1,3,5,7\}$ is related to any element of the subset $\{2,4,6\}$.

Solution Given any element $a$ in A, both $a$ and $a$ must be either odd or even, so that $(a, a) \in R$. Further, $(a, b) \in R \Rightarrow$ both $a$ and $b$ must be either odd or even $\Rightarrow(b, a) \in R$. Similarly, $(a, b) \in R$ and $(b, c) \in R \Rightarrow$ all elements $a, b, c$, must be either even or odd simultaneously $\Rightarrow(a, c) \in R$. Hence, $R$ is an equivalence relation. Further, all the elements of $\{1,3,5,7\}$ are related to each other, as all the elements of this subset are odd. Similarly, all the elements of the subset $\{2,4,6\}$ are related to each other, as all of them are even. Also, no element of the subset $\{1,3,5,7\}$ can be related to any element of $\{2,4,6\}$, as elements of $\{1,3,5,7\}$ are odd, while elements of $\{2,4,6\}$ are even.

EXERCISE 1.1

1. Determine whether each of the following relations are reflexive, symmetric and transitive:

(i) Relation $R$ in the set $A=\{1,2,3, \ldots, 13,14\}$ defined as

$$ R=\{(x, y): 3 x-y=0\} $$

(ii) Relation $R$ in the set $\mathbf{N}$ of natural numbers defined as

$$ R=\{(x, y): y=x+5 \text { and } x<4\} $$

(iii) Relation $R$ in the set $A=\{1,2,3,4,5,6\}$ as

$$ R=\{(x, y): y \text { is divisible by } x\} $$

(iv) Relation $R$ in the set $\mathbf{Z}$ of all integers defined as

$$ R=\{(x, y): x-y \text { is an integer }\} $$

(v) Relation $R$ in the set $A$ of human beings in a town at a particular time given by

(a) $R=\{(x, y): x \text { and } y \text { work at the same place } \}$

(b) $R=\{(x, y): x \text{ and } y \text{ live in the same locality } \}$

(c) $R=\{(x, y): x$ is exactly $7 cm$ taller than $y\}$

(d) $R=\{(x, y): x$ is wife of $y\}$

(e) $R=\{(x, y): x$ is father of $y\}$

Solution

(i) $A={1,2,3 \ldots 13,14}$

$R={(x, y): 3 x-y=0}$

$\therefore R={(1,3),(2,6),(3,9),(4,12)}$

$R$ is not reflexive since $(1,1),(2,2) \ldots(14,14) \notin R$.

Also, $R$ is not symmetric as $(1,3) \in R$, but $(3,1) \notin R$. $[3(3)-1 \neq 0$ ]

Also, $R$ is not transitive as $(1,3),(3,9) \in R$, but $(1,9) \notin R$.

$[3(1)-9 \neq 0]$

Hence, $R$ is neither reflexive, nor symmetric, nor transitive.

(ii) $R=\{(x, y): y=x+5 \quad \text{and} \quad x<4\}=\{(1,6),(2,7),(3,8)\}$

It is seen that $(1,1) \notin R$.

$\therefore R$ is not reflexive.

$(1,6) \in R$

But, $(1,6) \notin R$.

$\therefore R$ is not symmetric.

Now, since there is no pair in $R$ such that $(x, y)$ and $(y, z) \in R$ so, we need not look for the orderd pair ( $x, z$ ) in $R$.

$\therefore R$ is transitive

Hence, $R$ is neither reflexive, nor symmetric but it is transitive.

(iii) $A={1,2,3,4,5,6}$

$R=\{(x, y): y \quad \text{is divisible by} \quad x\}$

We know that any number $(x)$ is divisible by itself.

$\Rightarrow(x, x) \in R$

$\therefore R$ is reflexive.

Now,

$(2,4) \in R$ [as 4 is divisible by 2 ]

But,

$(4,2) \notin R$. [as 2 is not divisible by 4 ]

$\therefore R$ is not symmetric.

Let $(x, y),(y, z) \in R$. Then, $y$ is divisible by $x$ and $z$ is divisible by $y$.

$\therefore z$ is divisible by $x$.

$\Rightarrow(x, z) \in R$

$\therefore R$ is transitive.

Hence, $R$ is reflexive and transitive but not symmetric.

(iv) $R=\{(x, y): x-y \quad \text{is an integer} \}$

Now, for every $x \in \mathbf{Z},(x, x) \in R$ as $x-x=0$ is an integer.

$\therefore R$ is reflexive.

Now, for every $x, y \in \mathbf{Z}$ if $(x, y) \in \mathbf{R}$, then $x-y$ is an integer.

$\Rightarrow-(x-y)$ is also an integer.

$\Rightarrow(y-x)$ is an integer.

$\therefore(y, x) \in R$

$\therefore R$ is symmetric.

Now,

Let $(x, y)$ and $(y, z) \in R$, where $x, y, z \in \mathbf{Z}$.

$\Rightarrow(x-y)$ and $(y-z)$ are integers.

$\Rightarrow x-z=(x-y)+(y-z)$ is an integer. $\therefore(x, z) \in R$

$\therefore R$ is transitive.

Hence, $R$ is reflexive, symmetric, and transitive.

(v) (a) $R=\{(x, y): x \quad \text{and y work at the same place}\}$

$\Rightarrow(x, x) \in R$

$\therefore R$ is reflexive.

If $(x, y) \in R$, then $x$ and $y$ work at the same place.

$\Rightarrow y$ and $x$ work at the same place.

$\Rightarrow(y, x) \in R$.

$\therefore R$ is symmetric.

Now, let $(x, y),(y, z) \in R$

$\Rightarrow x$ and $y$ work at the same place and $y$ and $z$ work at the same place.

$\Rightarrow x$ and $z$ work at the same place.

$\Rightarrow(x, z) \in R$

$\therefore R$ is transitive.

Hence, $R$ is reflexive, symmetric, and transitive.

(b) $R=\{(x, y): x \quad \text{and y live in the same locality}\}$

Clearly $(x, x) \in R$ as $x$ and $x$ is the same human being.

$\therefore R$ is reflexive.

If $(x, y) \in R$, then $x$ and $y$ live in the same locality.

$\Rightarrow y$ and $x$ live in the same locality.

$\Rightarrow(y, x) \in R$

$\therefore R$ is symmetric.

Now, let $(x, y) \in R$ and $(y, z) \in R$.

$\Rightarrow x$ and $y$ live in the same locality and $y$ and $z$ live in the same locality.

$\Rightarrow x$ and $z$ live in the same locality.

$\Rightarrow(x, z) \in R$

$\therefore R$ is transitive.

Hence, $R$ is reflexive, symmetric, and transitive.

(c) $R=\{(x, y): x$ is exactly $7 cm$ taller than $y\}$

Now,

$(x, x) \notin R$

Since human being $x$ cannot be taller than himself. $\therefore R$ is not reflexive.

Now, let $(x, y) \in R$.

$\Rightarrow x$ is exactly $7 cm$ taller than $y$.

Then, $y$ is not taller than $x$.

$\therefore(y, x) \notin R$

Indeed if $x$ is exactly $7 cm$ taller than $y$, then $y$ is exactly $7 cm$ shorter than $x$.

$\therefore R$ is not symmetric.

Now,

Let $(x, y),(y, z) \in R$.

$\Rightarrow x$ is exactly $7 cm$ taller than $y$ and $y$ is exactly $7 cm$ taller than $z$.

$\Rightarrow x$ is exactly $14 cm$ taller than $z$.

$\therefore(x, z) \notin R$

$\therefore R$ is not transitive.

Hence, $R$ is neither reflexive, nor symmetric, nor transitive.

(d) $R=\{(x, y): x$ is the wife of $y\}$

Now,

$(x, x) \notin R$

Since $x$ cannot be the wife of herself.

$\therefore R$ is not reflexive.

Now, let $(x, y) \in R$

$\Rightarrow x$ is the wife of $y$.

Clearly $y$ is not the wife of $x$.

$\therefore(y, x) \notin R$

Indeed if $x$ is the wife of $y$, then $y$ is the husband of $x$.

$\therefore R$ is not transitive.

Let $(x, y),(y, z) \in R$

$\Rightarrow x$ is the wife of $y$ and $y$ is the wife of $z$.

This case is not possible. Also, this does not imply that $x$ is the wife of $z$.

$\therefore(x, z) \notin R$

$\therefore R$ is not transitive.

Hence, $R$ is neither reflexive, nor symmetric, nor transitive.

(e) $R=\{(x, y): x$ is the father of $y\}$

$(x, x) \notin R$

As $x$ cannot be the father of himself.

$\therefore R$ is not reflexive.

Now, let $(x, y) \in R$.

$\Rightarrow x$ is the father of $y$.

$\Rightarrow y$ cannot be the father of $y$.

Indeed, $y$ is the son or the daughter of $y$.

$\therefore(y, x) \notin R$

$\therefore R$ is not symmetric.

Now, let $(x, y) \in R$ and $(y, z) \in R$.

$\Rightarrow x$ is the father of $y$ and $y$ is the father of $z$.

$\Rightarrow x$ is not the father of $z$.

Indeed $x$ is the grandfather of $z$.

$\therefore(x, z) \notin R$

$\therefore R$ is not transitive.

Hence, $R$ is neither reflexive, nor symmetric, nor transitive.

2. Show that the relation $R$ in the set $\mathbf{R}$ of real numbers, defined as $R=\{(a, b): a \leq b^{2}\}$ is neither reflexive nor symmetric nor transitive.

Solution

$R={(a, b): a \leq b^{2}}$

It can be observed that $(\frac{1}{2}, \frac{1}{2}) \notin \mathbf{R}$, since $\frac{1}{2}>(\frac{1}{2})^{2}=\frac{1}{4}$.

$\therefore R$ is not reflexive.

Now, $(1,4) \in R$ as $1<4^{2}$

But, 4 is not less than $1^{2}$.

$\therefore(4,1) \notin R$

$\therefore R$ is not symmetric.

Now,

$(3,2),(2,1.5) \in R$

(as $3<2^{2}=4$ and $2<(1.5)^{2}=2.25$ )

But, $3>(1.5)^{2}=2.25$ $\therefore(3,1.5) \notin R$

$\therefore R$ is not transitive.

Hence, $R$ is neither reflexive, nor symmetric, nor transitive.

3. Check whether the relation $R$ defined in the set $\{1,2,3,4,5,6\}$ as $R=\{(a, b): b=a+1\}$ is reflexive, symmetric or transitive.

Solution

Let $A={1,2,3,4,5,6}$.

A relation $R$ is defined on set $A$ as:

$R={(a, b): b=a+1}$

$\therefore R={(1,2),(2,3),(3,4),(4,5),(5,6)}$

We can find $(a, a) \notin R$, where $a \in A$.

For instance,

$(1,1),(2,2),(3,3),(4,4),(5,5),(6,6) \notin R$

$\therefore R$ is not reflexive.

It can be observed that $(1,2) \in R$, but $(2,1) \notin R$.

$\therefore R$ is not symmetric.

Now, $(1,2),(2,3) \in \mathbf{R}$

But,

$(1,3) \notin R$

$\therefore R$ is not transitive

Hence, $R$ is neither reflexive, nor symmetric, nor transitive.

4. Show that the relation $R$ in $\mathbf{R}$ defined as $R=\{(a, b): a \leq b\}$, is reflexive and transitive but not symmetric.

Solution

$R={(a, b) ; a \leq b}$

Clearly $(a, a) \in R$ as $a=a$.

$\therefore R$ is reflexive.

Now,

$(2,4) \in R($ as $2<4)$

But, $(4,2) \notin R$ as 4 is greater than 2 .

$\therefore R$ is not symmetric.

Now, let $(a, b),(b, c) \in R$.

Then,

$a \leq b$ and $b \leq c$

$\Rightarrow a \leq c$

$\Rightarrow(a, c) \in R$

$\therefore R$ is transitive.

Hence, $R$ is reflexive and transitive but not symmetric.

5. Check whether the relation $R$ in $\mathbf{R}$ defined by $R=\{(a, b): a \leq b^{3}\}$ is reflexive, symmetric or transitive.

Solution

$R={(a, b): a \leq b^{3}}$

It is observed that $(\frac{1}{2}, \frac{1}{2}) \notin R$ as $\frac{1}{2}>(\frac{1}{2})^{3}=\frac{1}{8}$.

$\therefore R$ is not reflexive.

Now,

$(1,2) \in R(.$ as $.1<2^{3}=8)$

But,

$(2,1) \notin R(.$ as $.2^{3}>1)$

$\therefore R$ is not symmetric.

We have $(3, \frac{3}{2}),(\frac{3}{2}, \frac{6}{5}) \in R$ as $3<(\frac{3}{2})^{3}$ and $\frac{3}{2}<(\frac{6}{5})^{3}$.

But $(3, \frac{6}{5}) \notin R$ as $3>(\frac{6}{5})^{3}$.

$\therefore R$ is not transitive.

Hence, $R$ is neither reflexive, nor symmetric, nor transitive.

6. Show that the relation $R$ in the set $\{1,2,3\}$ given by $R=\{(1,2),(2,1)\}$ is symmetric but neither reflexive nor transitive.

Solution

Let $A={1,2,3}$.

A relation $R$ on $A$ is defined as $R={(1,2),(2,1)}$.

It is seen that $(1,1),(2,2),(3,3) \notin R$.

$\therefore R$ is not reflexive.

Now, as $(1,2) \in R$ and $(2,1) \in R$, then $R$ is symmetric.

Now, $(1,2)$ and $(2,1) \in R$

However,

$(1,1) \notin R$

$\therefore R$ is not transitive.

Hence, $R$ is symmetric but neither reflexive nor transitive.

7. Show that the relation $R$ in the set $A$ of all the books in a library of a college, given by $R=\{(x, y): x \text{ and } y \text{ have same number of pages} \}$ is an equivalence relation.

Solution

Set $A$ is the set of all books in the library of a college.

$R=\{x, y): x$ and $y$ have the same number of pages $\}$

Now, $R$ is reflexive since $(x, x) \in R$ as $x$ and $x$ has the same number of pages.

Let $(x, y) \in R \Rightarrow x$ and $y$ have the same number of pages.

$\Rightarrow y$ and $x$ have the same number of pages.

$\Rightarrow(y, x) \in R$

$\therefore R$ is symmetric.

Now, let $(x, y) \in R$ and $(y, z) \in R$.

$\Rightarrow x$ and $y$ and have the same number of pages and $y$ and $z$ have the same number of pages.

$\Rightarrow x$ and $z$ have the same number of pages.

$\Rightarrow(x, z) \in R$

$\therefore R$ is transitive.

Hence, $R$ is an equivalence relation.

8. Show that the relation $R$ in the set $A=\{1,2,3,4,5\}$ given by $R=\{(a, b):|a-b|$ is even $\}$, is an equivalence relation. Show that all the elements of $\{1,3,5\}$ are related to each other and all the elements of $\{2,4\}$ are related to each other. But no element of $\{1,3,5\}$ is related to any element of $\{2,4\}$.

Solution

$A={1,2,3,4,5}$

$R={(a, b):|a-b|$ is even $}$

It is clear that for any element $a \in A$, we have $|a-a|=0$ (which is even).

$\therefore R$ is reflexive.

Let $(a, b) \in R$.

$\Rightarrow|a-b|$ is even.

$\Rightarrow|-(a-b)|=|b-a|$ is also even.

$\Rightarrow(b, a) \in R$

$\therefore R$ is symmetric.

Now, let $(a, b) \in R$ and $(b, c) \in R$.

$\Rightarrow|a-b|$ is even and $|b-c|$ is even.

$\Rightarrow(a-b)$ is even and $(b-c)$ is even.

$\Rightarrow(a-c)=(a-b)+(b-c)$ is even. [Sum of two even integers is even]

$\Rightarrow|a-c|$ is even.

$\Rightarrow(a, c) \in R$

$\therefore R$ is transitive.

Hence, $R$ is an equivalence relation.

Now, all elements of the set ${1,2,3}$ are related to each other as all the elements of this subset are odd. Thus, the modulus of the difference between any two elements will be even.

Similarly, all elements of the set ${2,4}$ are related to each other as all the elements of this subset are even.

Also, no element of the subset ${1,3,5}$ can be related to any element of ${2,4}$ as all elements of ${1,3,5}$ are odd and all elements of ${2,4}$ are even. Thus, the modulus of the difference between the two elements (from each of these two subsets) will not be even.

9. Show that each of the relation $R$ in the set $A=\{x \in \mathbf{Z}: 0 \leq x \leq 12\}$, given by

(i) $R=\{(a, b):|a-b|$ $\text{is a multiple of 4} \}$

(ii) $R=\{(a, b): a=b \}$

is an equivalence relation. Find the set of all elements related to 1 in each case.

Solution

$ A={x \in \mathbf{Z}: 0 \leq x \leq 12}={0,1,2,3,4,5,6,7,8,9,10,11,12} $

(i) $R=\{(a, b):|a-b|$ $\text{is a multiple of 4} \}$

For any element $a \in A$, we have $(a, a) \in R$ as $|a-a|=0$ is a multiple of 4 .

$\therefore R$ is reflexive.

Now, let $(a, b) \in R \Rightarrow|a-b|$ is a multiple of 4 .

$\Rightarrow|-(a-b)|=|b-a|$ is a multiple of 4 .

$\Rightarrow(b, a) \in R$

$\therefore R$ is symmetric.

Now, let $(a, b),(b, c) \in R$.

$\Rightarrow|a-b|$ is a multiple of 4 and $|b-c|$ is a multiple of 4 .

$\Rightarrow(a-b)$ is a multiple of 4 and $(b-c)$ is a multiple of 4 .

$\Rightarrow(a-c)=(a-b)+(b-c)$ is a multiple of 4 .

$\Rightarrow|a-c|$ is a multiple of 4 .

$\Rightarrow(a, c) \in R$

$\therefore R$ is transitive.

Hence, $R$ is an equivalence relation.

The set of elements related to 1 is ${1,5,9}$ since $|1-1|=0$ is a multiple of 4 ,

$|5-1|=4$ is a multiple of 4 , and

$|9-1|=8$ is a multiple of 4 .

(ii) $R={(a, b): a=b}$

For any element $a \in A$, we have $(a, a) \in R$, since $a=a$.

$\therefore R$ is reflexive.

Now, let $(a, b) \in R$.

$\Rightarrow a=b$

$\Rightarrow b=a$

$\Rightarrow(b, a) \in R$

$\therefore R$ is symmetric.

Now, let $(a, b) \in R$ and $(b, c) \in R$.

$\Rightarrow a=b$ and $b=c$

$\Rightarrow a=c$

$\Rightarrow(a, c) \in R$

$\therefore R$ is transitive.

Hence, $R$ is an equivalence relation.

The elements in $R$ that are related to 1 will be those elements from set $A$ which are equal to 1.

Hence, the set of elements related to 1 is ${1}$.

10. Give an example of a relation. Which is

(i) Symmetric but neither reflexive nor transitive.

(ii) Transitive but neither reflexive nor symmetric.

(iii) Reflexive and symmetric but not transitive.

(iv) Reflexive and transitive but not symmetric.

(v) Symmetric and transitive but not reflexive.

Solution

(i) Let $A={5,6,7}$.

Define a relation $R$ on $A$ as $R={(5,6),(6,5)}$.

Relation $R$ is not reflexive as $(5,5),(6,6),(7,7) \notin R$.

Now, as $(5,6) \in R$ and also $(6,5) \in R, R$ is symmetric.

$\Rightarrow(5,6),(6,5) \in R$, but $(5,5) \notin R$

$\therefore R$ is not transitive.

Hence, relation $R$ is symmetric but not reflexive or transitive.

(ii)Consider a relation $\mathbf{R}$ in $\mathbf{R}$ defined as:

$R={(a, b): a<b}$

For any $a \in R$, we have $(a, a) \notin R$ since $a$ cannot be strictly less than $a$ itself. In fact, $a=$ a.

$\therefore R$ is not reflexive.

Now,

$(1,2) \in R($ as $1<2$ )

But, 2 is not less than 1 .

$\therefore(2,1) \notin R$

$\therefore R$ is not symmetric.

Now, let $(a, b),(b, c) \in R$.

$\Rightarrow a<b$ and $b<c$

$\Rightarrow a<c$

$\Rightarrow(a, c) \in R$

$\therefore R$ is transitive.

Hence, relation $R$ is transitive but not reflexive and symmetric.

(iii)Let $A={4,6,8}$.

Define a relation $R$ on $A$ as:

$A={(4,4),(6,6),(8,8),(4,6),(6,4),(6,8),(8,6)}$

Relation $R$ is reflexive since for every $a \in A,(a, a) \in R$ i.e., $(4,4),(6,6),(8,8) \in R$.

Relation $R$ is symmetric since $(a, b) \in R \Rightarrow(b, a) \in R$ for all $a, b \in R$.

Relation $R$ is not transitive since $(4,6),(6,8) \in R$, but $(4,8) \notin R$.

Hence, relation $R$ is reflexive and symmetric but not transitive.

(iv) Define a relation $R$ in $\mathbf{R}$ as:

$.R={a, b): a^{3} \geq b^{3}}$

Clearly $(a, a) \in R$ as $a^{3}=a^{3}$.

$\therefore R$ is reflexive.

Now,

$(2,1) \in R(.$ as $.2^{3} \geq 1^{3})$

But,

$(1,2) \notin R(.$ as $.1^{3}<2^{3})$

$\therefore R$ is not symmetric.

Now,

Let $(a, b),(b, c) \in R$.

$\Rightarrow a^{3} \geq b^{3}$ and $b^{3} \geq c^{3}$

$\Rightarrow a^{3} \geq c^{3}$

$\Rightarrow(a, c) \in R$

$\therefore R$ is transitive.

Hence, relation $R$ is reflexive and transitive but not symmetric.

(v) Let $A={-5,-6}$.

Define a relation $R$ on $A$ as:

$R={(-5,-6),(-6,-5),(-5,-5)}$

Relation $R$ is not reflexive as $(-6,-6) \notin R$.

Relation $R$ is symmetric as $(-5,-6) \in R$ and $(-6,-5) \in R$.

It is seen that $(-5,-6),(-6,-5) \in R$. Also, $(-5,-5) \in R$.

$\therefore$ The relation $R$ is transitive.

Hence, relation $R$ is symmetric and transitive but not reflexive.

11. Show that the relation $R$ in the set $A$ of points in a plane given by $R = \{(P, Q)$ : distance of the point $P$ from the origin is same as the distance of the point $Q$ from the origin $\}$, is an equivalence relation. Further, show that the set of all points related to a point $P \neq(0,0)$ is the circle passing through $P$ with origin as centre.

Solution

$R={(P, Q):$ distance of point $P$ from the origin is the same as the distance of point $Q$ from the origin }

Clearly, $(P, P) \in R$ since the distance of point $P$ from the origin is always the same as the distance of the same point $P$ from the origin.

$\therefore R$ is reflexive.

Now,

Let $(P, Q) \in R$. $\Rightarrow$ The distance of point $P$ from the origin is the same as the distance of point $Q$ from the origin.

$\Rightarrow$ The distance of point $Q$ from the origin is the same as the distance of point $P$ from the origin.

$\Rightarrow(Q, P) \in R$

$\therefore R$ is symmetric.

Now,

Let $(P, Q),(Q, S) \in R$.

$\Rightarrow$ The distance of points $P$ and $Q$ from the origin is the same and also, the distance of points $Q$ and $S$ from the origin is the same.

$\Rightarrow$ The distance of points $P$ and $S$ from the origin is the same.

$\Rightarrow(P, S) \in R$

$\therefore R$ is transitive.

Therefore, $R$ is an equivalence relation.

The set of all points related to $P \neq(0,0)$ will be those points whose distance from the origin is the same as the distance of point $P$ from the origin.

In other words, if $O(0,0)$ is the origin and $OP=k$, then the set of all points related to $P$ is at a distance of $k$ from the origin.

Hence, this set of points forms a circle with the centre as the origin and this circle passes through point $P$.

12. Show that the relation $R$ defined in the set $A$ of all triangles as $R=\{(T_{1}, T_{2}): T_{1}.$ is similar to $T_{2}\}$, is equivalence relation. Consider three right angle triangles $T_{1}$ with sides $3,4,5, T_{2}$ with sides $5,12,13$ and $T_{3}$ with sides $6,8,10$. Which triangles among $T_{1}, T_{2}$ and $T_{3}$ are related?

Solution

$R={(T_1, T_2): T_1.$ is similar to $.T_2}$

$R$ is reflexive since every triangle is similar to itself.

Further, if $(T_1, T_2) \in R$, then $T_1$ is similar to $T_2$.

$\Rightarrow T_2$ is similar to $T_1$

$\Rightarrow(T_2, T_1) \in R$

$\therefore R$ is symmetric.

Now,

Let $(T_1, T_2),(T_2, T_3) \in R$.

$\Rightarrow T_1$ is similar to $T_2$ and $T_2$ is similar to $T_3$.

$\Rightarrow T_1$ is similar to $T_3$

$\Rightarrow(T_1, T_3) \in R$

$\therefore R$ is transitive.

Thus, $R$ is an equivalence relation.

Now, we can observe that:

$ \frac{3}{6}=\frac{4}{8}=\frac{5}{10}(=\frac{1}{2}) $

$\therefore$ The corresponding sides of triangles $T_1$ and $T_3$ are in the same ratio.

Then, triangle $T_1$ is similar to triangle $T_3$.

Hence, $T_1$ is related to $T_3$.

13. Show that the relation $R$ defined in the set $A$ of all polygons as $R=\{(P_{1}, P_{2})$ : $P_{1}$ and $P_{2}$ have same number of sides $\}$, is an equivalence relation. What is the set of all elements in A related to the right angle triangle T with sides 3, 4 and 5?

Solution

$R=\{(P_1, P_2): P_1.$ and $P_2$ have same the number of sides $\}$

$R$ is reflexive since $(P_1, P_1) \in R$ as the same polygon has the same number of sides with itself.

Let $(P_1, P_2) \in R$.

$\Rightarrow P_1$ and $P_2$ have the same number of sides.

$\Rightarrow P_2$ and $P_1$ have the same number of sides.

$\Rightarrow(P_2, P_1) \in R$

$\therefore R$ is symmetric.

Now,

Let $(P_1, P_2),(P_2, P_3) \in R$.

$\Rightarrow P_1$ and $P_2$ have the same number of sides. Also, $P_2$ and $P_3$ have the same number of sides.

$\Rightarrow P_1$ and $P_3$ have the same number of sides.

$\Rightarrow(P_1, P_3) \in R$ $\therefore R$ is transitive.

Hence, $R$ is an equivalence relation.

The elements in $A$ related to the right-angled triangle $(T)$ with sides 3,4 , and 5 are those polygons which have 3 sides (since $T$ is a polygon with 3 sides).

Hence, the set of all elements in $A$ related to triangle $T$ is the set of all triangles.

14. Let $L$ be the set of all lines in $XY$ plane and $R$ be the relation in $L$ defined as $R=\{(L_{1}, L_{2}): L_{1}$ is parallel to $L_{2}\}$. Show that $R$ is an equivalence relation. Find the set of all lines related to the line $y=2 x+4$.

Solution

$R=\{(L_1, L_2): L_1.$ is parallel to $.L_2\}$

$R$ is reflexive as any line $L_1$ is parallel to itself i.e., $(L_1, L_1) \in R$.

Now,

Let $(L_1, L_2) \in R$.

$\Rightarrow L_1$ is parallel to $L_2$.

$\Rightarrow L_2$ is parallel to $L_1$.

$\Rightarrow(L_2, L_1) \in R$

$\therefore R$ is symmetric.

Now,

Let $(L_1, L_2),(L_2, L_3) \in R$.

$\Rightarrow L_1$ is parallel to $L_2$. Also, $L_2$ is parallel to $L_3$.

$\Rightarrow L_1$ is parallel to $L_3$.

$\therefore R$ is transitive.

Hence, $R$ is an equivalence relation.

The set of all lines related to the line $y=2 x+4$ is the set of all lines that are parallel to the line $y=2 x+4$.

Slope of line $y=2 x+4$ is $m=2$

It is known that parallel lines have the same slopes.

The line parallel to the given line is of the form $y=2 x+c$, where $c \in \mathbf{R}$.

Hence, the set of all lines related to the given line is given by $y=2 x+c$, where $c \in \mathbf{R}$.

15. Let $R$ be the relation in the set $\{1,2,3,4\}$ given by $R=\{(1,2),(2,2),(1,1),(4,4)$, $(1,3),(3,3),(3,2)\}$. Choose the correct answer.

(A) $R$ is reflexive and symmetric but not transitive.

(B) $R$ is reflexive and transitive but not symmetric.

(C) $R$ is symmetric and transitive but not reflexive.

(D) $R$ is an equivalence relation.

Solution

$R={(1,2),(2,2),(1,1),(4,4),(1,3),(3,3),(3,2)}$

It is seen that $(a, a) \in \mathbf{R}$, for every $a \in{1,2,3,4}$.

$\therefore R$ is reflexive.

It is seen that $(1,2) \in R$, but $(2,1) \notin R$.

$\therefore R$ is not symmetric.

Also, it is observed that $(a, b),(b, c) \in R \Rightarrow(a, c) \in R$ for all $a, b, c \in{1,2,3,4}$.

$\therefore R$ is transitive.

Hence, $R$ is reflexive and transitive but not symmetric.

The correct answer is $B$.

16. Let $R$ be the relation in the set $\mathbf{N}$ given by $R=\{(a, b): a=b-2, b>6\}$. Choose the correct answer. (A) $(2,4) \in R$ (B) $(3,8) \in R$ (C) $(6,8) \in R$ (D) $(8,7) \in R$

Solution

$R={(a, b): a=b-2, b>6}$

Now, since $b>6,(2,4) \notin R$

Also, as $3 \neq 8-2,(3,8) \notin R$

And, as $8 \neq 7-2$

$\therefore(8,7) \notin R$

Now, consider $(6,8)$.

We have $8>6$ and also, $6=8-2$.

$\therefore(6,8) \in R$

The correct answer is $C$.

1.3 Types of Functions

The notion of a function along with some special functions like identity function, constant function, polynomial function, rational function, modulus function, signum function etc. along with their graphs have been given in Class XI.

Addition, subtraction, multiplication and division of two functions have also been studied. As the concept of function is of paramount importance in mathematics and among other disciplines as well, we would like to extend our study about function from where we finished earlier. In this section, we would like to study different types of functions.

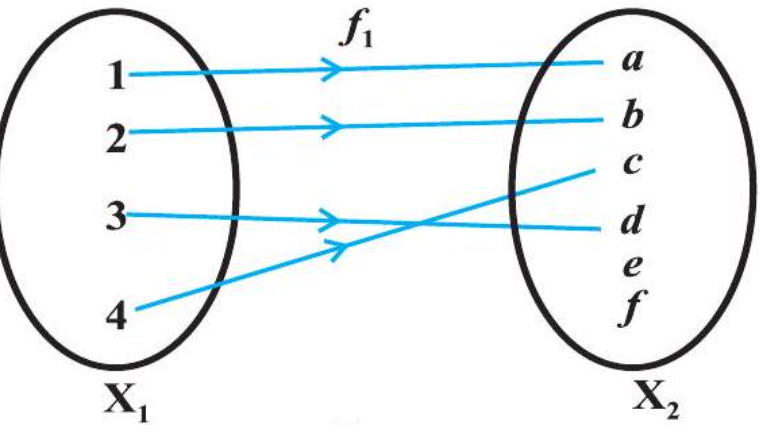
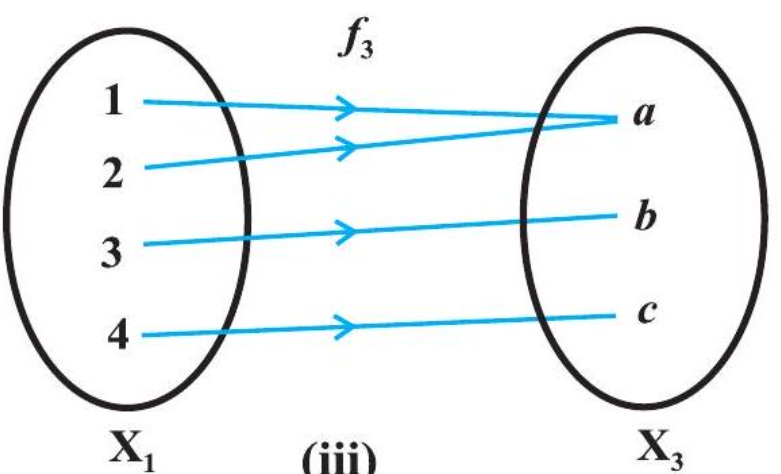
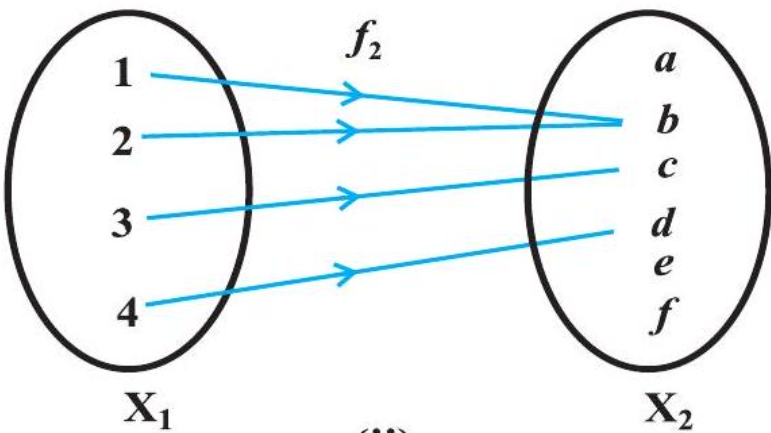
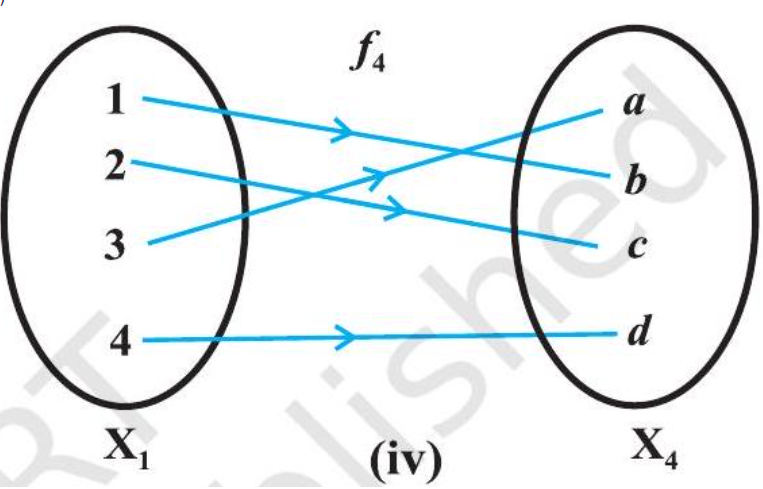
Consider the functions $f_{1}, f_{2}, f_{3}$ and $f_{4}$ given by the following diagrams.

In Fig 1.2, we observe that the images of distinct elements of $X_{1}$ under the function $f_{1}$ are distinct, but the image of two distinct elements 1 and 2 of $X_{1}$ under $f_{2}$ is same, namely $b$. Further, there are some elements like $e$ and $f$ in $X_{2}$ which are not images of any element of $X_{1}$ under $f_{1}$, while all elements of $X_{3}$ are images of some elements of $X_{1}$ under $f_{3}$. The above observations lead to the following definitions:

Definition 5 $ A$ function $f: X \rightarrow Y$ is defined to be one-one (or injective), if the images of distinct elements of $X$ under $f$ are distinct, i.e., for every $x_{1}, x_{2} \in X, f(x_{1})=f(x_{2})$ implies $x_{1}=x_{2}$. Otherwise, $f$ is called many-one.

The function $f_{1}$ and $f_{4}$ in Fig 1.2 (i) and (iv) are one-one and the function $f_{2}$ and $f_{3}$ in Fig 1.2 (ii) and (iii) are many-one.

Definition 6 A function $f: X \rightarrow Y$ is said to be onto (or surjective), if every element of $Y$ is the image of some element of $X$ under $f$, i.e., for every $y \in Y$, there exists an element $x$ in $X$ such that $f(x)=y$.

The function $f_{3}$ and $f_{4}$ in Fig 1.2 (iii), (iv) are onto and the function $f_{1}$ in Fig 1.2 (i) is not onto as elements $e, f$ in $X_{2}$ are not the image of any element in $X_{1}$ under $f_{1}$.

(i)

(iii)

(ii)

(iv)

Fig 1.2 (i) to (iv)

Remark $f: X \rightarrow Y$ is onto if and only if Range of $f=Y$.

Definition 7 A function $f: X \rightarrow Y$ is said to be one-one and onto (or bijective), if $f$ is both one-one and onto.

The function $f_{4}$ in Fig 1.2 (iv) is one-one and onto.

Example 7 Let A be the set of all 50 students of Class $X$ in a school. Let $f: A \rightarrow \mathbf{N}$ be function defined by $f(x)=$ roll number of the student $x$. Show that $f$ is one-one but not onto.

Solution No two different students of the class can have same roll number. Therefore, $f$ must be one-one. We can assume without any loss of generality that roll numbers of students are from 1 to 50 . This implies that 51 in $\mathbf{N}$ is not roll number of any student of the class, so that 51 can not be image of any element of $X$ under $f$. Hence, $f$ is not onto.

Example 8 Show that the function $f: \mathbf{N}\rightarrow \mathbf{N}$, given by $f(x)=2 x$, is one-one but not onto.

Solution The function $f$ is one-one, for $f(x_{1})=f(x_{2}) \Rightarrow 2 x_{1}=2 x_{2} \Rightarrow x_{1}=x_{2}$. Further, $f$ is not onto, as for $1 \in \mathbf{N}$, there does not exist any $x$ in $\mathbf{N}$ such that $f(x)=2 x=1$.

Example 9 Prove that the function $f: \mathbf{R} \rightarrow \mathbf{R}$, given by $f(x)=2 x$, is one-one and onto. Solution $f$ is one-one, as $f(x_{1})=f(x_{2}) \Rightarrow 2 x_{1}=2 x_{2} \Rightarrow x_{1}=x_{2}$. Also, given any real number $y$ in $R$, there exists $\frac{y}{2}$ in $R$ such that $f(\frac{y}{2})=2 .(\frac{y}{2})=y$. Hence, $f$ is onto.

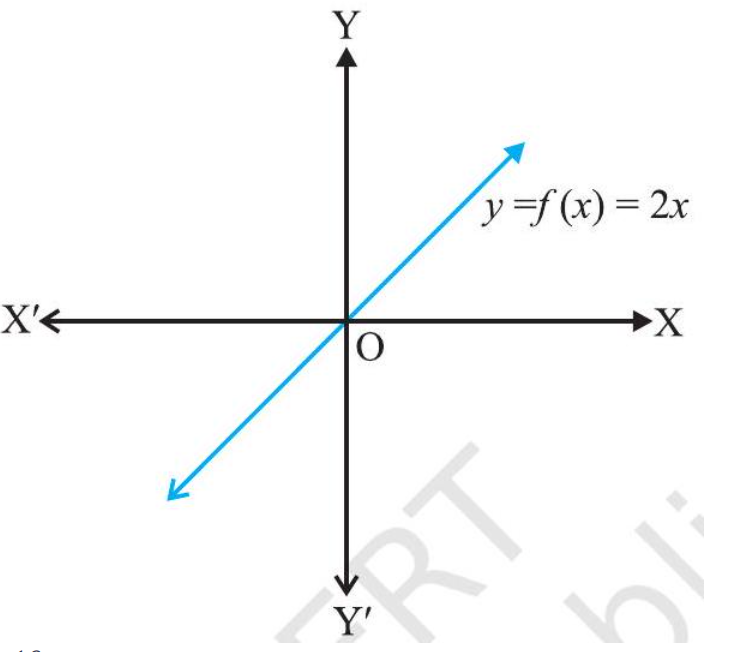
Fig 1.3

Example 10 Show that the function $f: \mathbf{N} \rightarrow \mathbf{N}$, given by $f(1)=f(2)=1$ and $f(x)=x-1$, for every $x>2$, is onto but not one-one.

Solution $f$ is not one-one, as $f(1)=f(2)=1$. But $f$ is onto, as given any $y \in \mathbf{N}, y \neq 1$, we can choose $x$ as $y+1$ such that $f(y+1)=y+1-1=y$. Also for $1 \in \mathbf{N}$, we have $f(1)=1$.

Example 11 Show that the function $f: \mathbf{R} \rightarrow \mathbf{R}$, defined as $f(x)=x^{2}$, is neither one-one nor onto.

Solution Since $f(-1)=1=f(1), f$ is not oneone. Also, the element -2 in the co-domain $\mathbf{R}$ is not image of any element $x$ in the domain $\mathbf{R}$ (Why?). Therefore $f$ is not onto.

Example 12 Show that $f: \mathbf{N} \rightarrow \mathbf{N}$, given by

$$ f(x)=\begin{aligned} & x+1, \text { if } x \text { is odd, } \\ & x-1, \text { if } x \text { is even } \end{aligned} $$

is both one-one and onto.

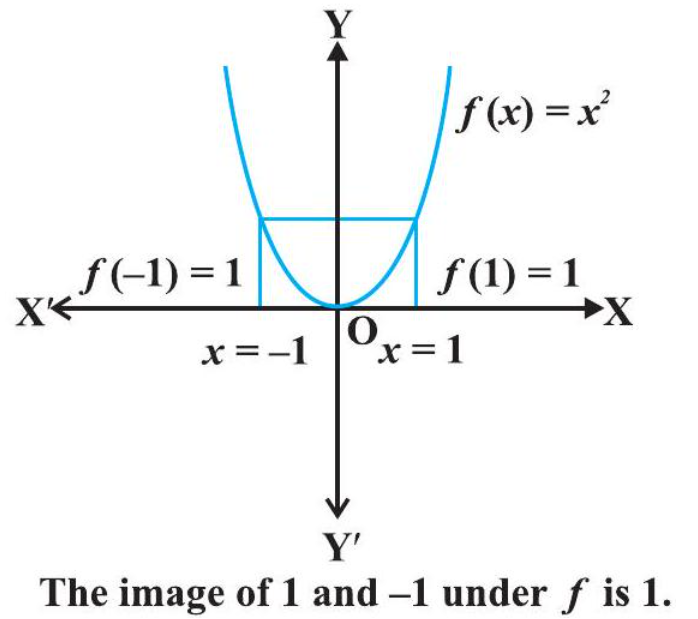
Fig 1.4

Solution Suppose $f(x_{1})=f(x_{2})$. Note that if $x_{1}$ is odd and $x_{2}$ is even, then we will have $x_{1}+1=x_{2}-1$, i.e., $x_{2}-x_{1}=2$ which is impossible. Similarly, the possibility of $x_{1}$ being even and $x_{2}$ being odd can also be ruled out, using the similar argument. Therefore, both $x_{1}$ and $x_{2}$ must be either odd or even. Suppose both $x_{1}$ and $x_{2}$ are odd. Then $f(x_{1})=f(x_{2}) \Rightarrow x_{1}+1=x_{2}+1 \Rightarrow x_{1}=x_{2}$. Similarly, if both $x_{1}$ and $x_{2}$ are even, then also $f(x_{1})=f(x_{2}) \Rightarrow x_{1}-1=x_{2}-1 \Rightarrow x_{1}=x_{2}$. Thus, $f$ is one-one. Also, any odd number $2 r+1$ in the co-domain $\mathbf{N}$ is the image of $2 r+2$ in the domain $\mathbf{N}$ and any even number $2 r$ in the co-domain $\mathbf{N}$ is the image of $2 r-1$ in the domain $\mathbf{N}$. Thus, $f$ is onto.

Example 13 Show that an onto function $f:\{1,2,3\} \Rightarrow\{1,2,3\}$ is always one-one.

Solution Suppose $f$ is not one-one. Then there exists two elements, say 1 and 2 in the domain whose image in the co-domain is same. Also, the image of 3 under $f$ can be only one element. Therefore, the range set can have at the most two elements of the co-domain $\{1,2,3\}$, showing that $f$ is not onto, a contradiction. Hence, $f$ must be one-one.

Example 14 Show that a one-one function $f:\{1,2,3\} \rightarrow\{1,2,3\}$ must be onto.

Solution Since $f$ is one-one, three elements of $\{1,2,3\}$ must be taken to 3 different elements of the co-domain $\{1,2,3\}$ under $f$. Hence, $f$ has to be onto.

Remark The results mentioned in Examples 13 and 14 are also true for an arbitrary finite set $X$, i.e., a one-one function $f: X \rightarrow X$ is necessarily onto and an onto map $f: X \rightarrow X$ is necessarily one-one, for every finite set $X$. In contrast to this, Examples 8 and 10 show that for an infinite set, this may not be true. In fact, this is a characteristic difference between a finite and an infinite set.

EXERCISE 1.2

1. Show that the function $f: \mathbf{R} \rightarrow \mathbf{R}$ defined by $f(x)=\frac{1}{x}$ is one-one and onto, where $\mathbf{R}$ is the set of all non-zero real numbers. Is the result true, if the domain $\mathbf{R}$ is replaced by $\mathbf{N}$ with co-domain being same as $\mathbf{R}$ ?

Solution

It is given that $f: \mathbf{R} * \to \mathbf{R} *$ is defined by $f(x)=\frac{1}{x}$.

One-one:

$ \begin{aligned} & f(x)=f(y) \\ & \Rightarrow \frac{1}{x}=\frac{1}{y} \\ & \Rightarrow x=y \end{aligned} $

$\therefore f$ is one-one.

Onto:

It is clear that for $y \in \mathbf{R} _{*}$, there exists $x=\frac{1}{y} \in \mathbf{R}$. (Exists as $.y \neq 0)$ such that

$ f(x)=\frac{1}{(\frac{1}{y})}=y . $

$\therefore f$ is onto.

Thus, the given function $(f)$ is one-one and onto.

Now, consider function $g: \mathbf{N} \to \mathbf{R} *$ defined by

$ g(x)=\frac{1}{x} $

We have,

$ g(x_1)=g(x_2) \Rightarrow \frac{1}{x_1}=\frac{1}{x_2} \Rightarrow x_1=x_2 $

$\therefore g$ is one-one.

Further, it is clear that $g$ is not onto as for $1.2 \in \mathbf{R} *$ there does not exit any $x$ in $\mathbf{N}$ such

that $g(x)=\frac{1}{1.2}$.

Hence, function $g$ is one-one but not onto.

2. Check the injectivity and surjectivity of the following functions:

(i) $f: \mathbf{N} \rightarrow \mathbf{N}$ given by $f(x)=x^{2}$

(ii) $f: \mathbf{Z} \rightarrow \mathbf{Z}$ given by $f(x)=x^{2}$

(iii) $f: \mathbf{R} \rightarrow \mathbf{R}$ given by $f(x)=x^{2}$

(iv) $f: \mathbf{N} \rightarrow \mathbf{N}$ given by $f(x)=x^{3}$

(v) $f: \mathbf{Z} \rightarrow \mathbf{Z}$ given by $f(x)=x^{3}$

Solution

(i) $f: \mathbf{N} \to \mathbf{N}$ is given by,

$f(x)=x^{2}$

It is seen that for $x, y \in \mathbf{N}, f(x)=f(y) \Rightarrow x^{2}=y^{2} \Rightarrow x=y$.

$\therefore f$ is injective.

Now, $2 \in \mathbf{N}$. But, there does not exist any $x$ in $\mathbf{N}$ such that $f(x)=x^{2}=2$.

$\therefore f$ is not surjective.

Hence, function $f$ is injective but not surjective.

(ii) $f: \mathbf{Z} \to \mathbf{Z}$ is given by,

$f(x)=x^{2}$

It is seen that $f(-1)=f(1)=1$, but $-1 \neq 1$.

$\therefore f$ is not injective.

Now, $-2 \in \mathbf{Z}$. But, there does not exist any element $x \in \mathbf{Z}$ such that $f(x)=x^{2}=-2$.

$\therefore f$ is not surjective.

Hence, function $f$ is neither injective nor surjective.

(iii) $f: \mathbf{R} \to \mathbf{R}$ is given by,

$f(x)=x^{2}$

It is seen that $f(-1)=f(1)=1$, but $-1 \neq 1$.

$\therefore f$ is not injective.

Now, $-2 \in \mathbf{R}$. But, there does not exist any element $x \in \mathbf{R}$ such that $f(x)=x^{2}=-2$. $\therefore f$ is not surjective.

Hence, function $f$ is neither injective nor surjective.

(iv) $f: \mathbf{N} \to \mathbf{N}$ given by,

$f(x)=x^{3}$

It is seen that for $x, y \in \mathbf{N}, f(x)=f(y) \Rightarrow x^{3}=y^{3} \Rightarrow x=y$.

$\therefore f$ is injective.

Now, $2 \in \mathbf{N}$. But, there does not exist any element $x$ in domain $\mathbf{N}$ such that $f(x)=x^{3}=$

$\therefore f$ is not surjective

Hence, function $f$ is injective but not surjective.

(v) $f: \mathbf{Z} \to \mathbf{Z}$ is given by,

$f(x)=x^{3}$

It is seen that for $x, y \in \mathbf{Z}, f(x)=f(y) \Rightarrow x^{3}=y^{3} \Rightarrow x=y$.

$\therefore f$ is injective.

Now, $2 \in \mathbf{Z}$. But, there does not exist any element $x$ in domain $\mathbf{Z}$ such that $f(x)=x^{3}=2$.

$\therefore f$ is not surjective.

Hence, function $f$ is injective but not surjective.

3. Prove that the Greatest Integer Function $f: \mathbf{R} \rightarrow \mathbf{R}$, given by $f(x)=[x]$, is neither one-one nor onto, where $[x]$ denotes the greatest integer less than or equal to $x$.

Solution

$f: \mathbf{R} \to \mathbf{R}$ is given by,

$f(x)=[x]$

It is seen that $f(1.2)=[1.2]=1, f(1.9)=[1.9]=1$.

$\therefore f(1.2)=f(1.9)$, but $1.2 \neq 1.9$.

$\therefore f$ is not one-one.

Now, consider $0.7 \in \mathbf{R}$.

It is known that $f(x)=[x]$ is always an integer. Thus, there does not exist any element $x$ $\in \mathbf{R}$ such that $f(x)=0.7$.

$\therefore f$ is not onto.

Hence, the greatest integer function is neither one-one nor onto.

4. Show that the Modulus Function $f: \mathbf{R} \rightarrow \mathbf{R}$, given by $f(x)=|x|$, is neither oneone nor onto, where $|x|$ is $x$, if $x$ is positive or 0 and $|x|$ is $-x$, if $x$ is negative.

Solution

$f: \mathbf{R} \to \mathbf{R}$ is given by,

$f(x)=|x|=\begin{cases} x, \text{ if } x \geq 0 \\ -x, \text{ if } x<0 \end{cases} .$

It is seen that $f(-1)=|-1|=1, f(1)=|1|=1$.

$\therefore f(-1)=f(1)$, but $-1 \neq 1$.

$\therefore f$ is not one-one.

Now, consider $-1 \in \mathbf{R}$.

It is known that $f(x)=|x|$ is always non-negative. Thus, there does not exist any element $x$ in domain $\mathbf{R}$ such that $f(x)=|x|=-1$.

$\therefore f$ is not onto.

Hence, the modulus function is neither one-one nor onto.

5. Show that the Signum Function $f: \mathbf{R} \rightarrow \mathbf{R}$, given by

$$ \begin{array}{r} 1, \text { if } x>0 \\ f(x)=0, \text { if } x=0 \\ 1, \text { if } x<0 \end{array} $$

is neither one-one nor onto.

Solution

$f: \mathbf{R} \to \mathbf{R}$ is given by,

$$ f(x)=\begin{matrix} 1, \text{ if } x>0 \\ 0, \text{ if } x=0 \\ -1, \text{ if } x<0 \end{matrix} $$

It is seen that $f(1)=f(2)=1$, but $1 \neq 2$.

$\therefore f$ is not one-one.

Now, as $f(x)$ takes only 3 values $(1,0$, or -1 ) for the element -2 in co-domain $\mathbf{R}$, there does not exist any $x$ in domain $\mathbf{R}$ such that $f(x)=-2$.

$\therefore f$ is not onto.

Hence, the signum function is neither one-one nor onto.

6. Let $A=\{1,2,3\}, B=\{4,5,6,7\}$ and let $f=\{(1,4),(2,5),(3,6)\}$ be a function from $A$ to $B$. Show that $f$ is one-one.

Solution

It is given that $A={1,2,3}, B={4,5,6,7}$.

$f: A \to B$ is defined as $f={(1,4),(2,5),(3,6)}$.

$\therefore f(1)=4, f(2)=5, f(3)=6$

It is seen that the images of distinct elements of $A$ under $f$ are distinct.

Hence, function $f$ is one-one.

7. In each of the following cases, state whether the function is one-one, onto or bijective. Justify your answer.

(i) $f: \mathbf{R} \rightarrow \mathbf{R}$ defined by $f(x)=3-4 x$

(ii) $f: \mathbf{R} \rightarrow \mathbf{R}$ defined by $f(x)=1+x^{2}$

Solution

(i) $f: \mathbf{R} \to \mathbf{R}$ is defined as $f(x)=3-4 x$.

Let $x_1, x_2 \in \mathbf{R}$ such that $f(x_1)=f(x_2)$.

$\Rightarrow 3-4 x_1=3-4 x_2$

$\Rightarrow-4 x_1=-4 x_2$

$\Rightarrow x_1=x_2$

$\therefore f$ is one-one.

For any real number $(y)$ in $\mathbf{R}$, there exists $\frac{3-y}{4}$ in $\mathbf{R}$ such that

$f(\frac{3-y}{4})=3-4(\frac{3-y}{4})=y$.

$\therefore f$ is onto.

Hence, $f$ is bijective.

(ii) $f: \mathbf{R} \to \mathbf{R}$ is defined as

$ f(x)=1+x^{2} . $

Let $x_1, x_2 \in \mathbf{R}$ such that $f(x_1)=f(x_2)$.

$\Rightarrow 1+x_1^{2}=1+x_2^{2}$

$\Rightarrow x_1^{2}=x_2^{2}$

$\Rightarrow x_1= \pm x_2$

$\therefore f(x_1)=f(x_2)$ does not imply that $x_1=x_2$.

For instance,

$ f(1)=f(-1)=2 $

$\therefore f$ is not one-one.

Consider an element -2 in co-domain $\mathbf{R}$.

It is seen that $f(x)=1+x^{2}$ is positive for all $x \in \mathbf{R}$.

Thus, there does not exist any $x$ in domain $\mathbf{R}$ such that $f(x)=-2$.

$\therefore f$ is not onto.

Hence, $f$ is neither one-one nor onto.

8. Let $A$ and $B$ be sets. Show that $f: A \times B \rightarrow B \times A$ such that $f(a, b)=(b, a)$ is bijective function.

Solution

$f: A \times B \to B \times A$ is defined as $f(a, b)=(b, a)$.

Let $(a_1, b_1),(a_2, b_2) \in A \times B$ such that $f(a_1, b_1)=f(a_2, b_2)$

$\Rightarrow(b_1, a_1)=(b_2, a_2)$

$\Rightarrow b_1=b_2$ and $a_1=a_2$

$\Rightarrow(a_1, b_1)=(a_2, b_2)$

$\therefore f$ is one-one.

Now, let $(b, a) \in B \times A$ be any element.

Then, there exists $(a, b) \in A \times B$ such that $f(a, b)=(b, a)$. [By definition of $f$ ] $\therefore f$ is onto.

Hence, $f$ is bijective.

9. Let $f: \mathbf{N} \to \mathbf{N}$ be defined by $f(n)=\begin{cases} \frac{n+1}{2}, & \text{ if } n \text{ is odd } \\ \frac{n}{2}, & \text{ if } n \text{ is even } \end{cases} .$ for all $n \in \mathbf{N}$.

State whether the function $f$ is bijective. Justify your answer.

Solution

$ f(n)=\begin{matrix} \frac{n+1}{2}, & \text{ if } n \text{ is odd } \\ \frac{n}{2}, & \text{ if } n \text{ is even }\\ \end{matrix} \text{ for all } n \in \mathbf{N}. $

It can be observed that:

$f(1)=\frac{1+1}{2}=1$ and $f(2)=\frac{2}{2}=1 \quad[$ By definition of $f]$

$\therefore f(1)=f(2)$, where $1 \neq 2$.

$\therefore f$ is not one-one.

Consider a natural number $(n)$ in co-domain $\mathbf{N}$.

Case I: $n$ is odd

$\therefore n=2 r+1$ for some $r \in \mathbf{N}$. Then, there exists $4 r+1 \in \mathbf{N}$ such that

$ f(4 r+1)=\frac{4 r+1+1}{2}=2 r+1 $

Case II: $n$ is even

$\therefore n=2 r$ for some $r \in \mathbf{N}$. Then, there exists $4 r \in \mathbf{N}$ such that $f(4 r)=\frac{4 r}{2}=2 r$.

$\therefore f$ is onto.

Hence, $f$ is not a bijective function.

10. Let $A=\mathbf{R}-\{3\}$ and $B=\mathbf{R}-\{1\}$. Consider the function $f: A \rightarrow B$ defined by $f(x)=(\frac{x-2}{x-3})$. Is $f$ one-one and onto? Justify your answer.

Solution

$A=\mathbf{R}-{3}, B=\mathbf{R}-{1}$

$f: A \to B$ is defined as $f(x)=(\frac{x-2}{x-3})$.

Let $x, y \in$ A such that $f(x)=f(y)$.

$\Rightarrow \frac{x-2}{x-3}=\frac{y-2}{y-3}$

$\Rightarrow(x-2)(y-3)=(y-2)(x-3)$

$\Rightarrow x y-3 x-2 y+6=x y-3 y-2 x+6$

$\Rightarrow-3 x-2 y=-3 y-2 x$

$\Rightarrow 3 x-2 x=3 y-2 y$

$\Rightarrow x=y$

$\therefore f$ is one-one.

Let $y \in B=\mathbf{R}-{1}$. Then, $y \neq 1$.

The function $f$ is onto if there exists $x \in A$ such that $f(x)=y$.

Now,

$ \begin{aligned} & f(x)=y \\ & \Rightarrow \frac{x-2}{x-3}=y \\ & \Rightarrow x-2=x y-3 y \\ & \Rightarrow x(1-y)=-3 y+2 \\ & \Rightarrow x=\frac{2-3 y}{1-y} \in A \quad[y \neq 1] \end{aligned} $

Thus, for any $y \in B$, there exists $\frac{2-3 y}{1-y} \in A$ such that $f(\frac{2-3 y}{1-y})=\frac{(\frac{2-3 y}{1-y})-2}{(\frac{2-3 y}{1-y})-3}=\frac{2-3 y-2+2 y}{2-3 y-3+3 y}=\frac{-y}{-1}=y$.

$\therefore f$ is onto.

Hence, function $f$ is one-one and onto.

11. Let $f: \mathbf{R} \rightarrow \mathbf{R}$ be defined as $f(x)=x^{4}$. Choose the correct answer.

(A) $f$ is one-one onto

(B) $f$ is many-one onto

(C) $f$ is one-one but not onto

(D) $f$ is neither one-one nor onto.

Solution

$f: \mathbf{R} \to \mathbf{R}$ is defined as $f(x)=x^{4}$.

Let $x, y \in \mathbf{R}$ such that $f(x)=f(y)$.

$\Rightarrow x^{4}=y^{4}$

$\Rightarrow x= \pm y$

$\therefore f(x_1)=f(x_2)$ does not imply that $x_1=x_2$.

For instance,

$ f(1)=f(-1)=1 $

$\therefore f$ is not one-one.

Consider an element 2 in co-domain $\mathbf{R}$. It is clear that there does not exist any $x$ in domain $\mathbf{R}$ such that $f(x)=2$.

$\therefore f$ is not onto.

Hence, function $f$ is neither one-one nor onto.

The correct answer is D.

12. Let $f: \mathbf{R} \rightarrow \mathbf{R}$ be defined as $f(x)=3 x$. Choose the correct answer.

(A) $f$ is one-one onto

(B) $f$ is many-one onto

(C) $f$ is one-one but not onto

(D) $f$ is neither one-one nor onto.

Solution

$f: \mathbf{R} \to \mathbf{R}$ is defined as $f(x)=3 x$.

Let $x, y \in \mathbf{R}$ such that $f(x)=f(y)$.

$\Rightarrow 3 x=3 y$

$\Rightarrow x=y$

$\therefore f$ is one-one.

Also, for any real number $(y)$ in co-domain $\mathbf{R}$, there exists $\frac{y}{3}$ in $\mathbf{R}$ such that $f(\frac{y}{3})=3(\frac{y}{3})=y$.

$\therefore f$ is onto.

Hence, function $f$ is one-one and onto.

The correct answer is A.

1.4 Composition of Functions and Invertible Function

In this section, we will study composition of functions and the inverse of a bijective function. Consider the set A of all students, who appeared in Class X of a Board Examination in 2006. Each student appearing in the Board Examination is assigned a roll number by the Board which is written by the students in the answer script at the time of examination. In order to have confidentiality, the Board arranges to deface the roll numbers of students in the answer scripts and assigns a fake code number to each roll number. Let $\mathrm{B} \subset \mathbf{N}$ be the set of all roll numbers and $\mathrm{C} \subset \mathbf{N}$ be the set of all code numbers. This gives rise to two functions $f: \mathrm{A} \rightarrow \mathrm{B}$ and $g: \mathrm{B} \rightarrow \mathrm{C}$ given by $f(a)=$ the roll number assigned to the student $a$ and $g(b)=$ the code number assigned to the roll number $b$. In this process each student is assigned a roll number through the function $f$ and each roll number is assigned a code number through the function $g$. Thus, by the combination of these two functions, each student is eventually attached a code number.
This leads to the following definition:

Definition 8 Let $f: A \rightarrow B$ and $g: B \rightarrow C$ be two functions. Then the composition of $f$ and $g$, denoted by $g \circ f$, is defined as the function $g \circ f: A \rightarrow C$ given by

$$ g o f(x)=g(f(x)), \forall x \in A . $$

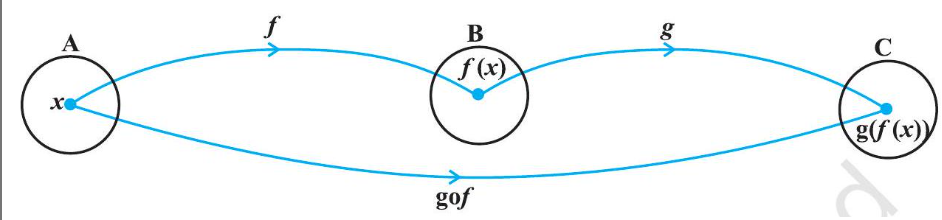
Fig 1.5

Example 15 Let $f:\{2,3,4,5\} \rightarrow\{3,4,5,9\}$ and $g:\{3,4,5,9\} \rightarrow\{7,11,15\}$ be functions defined as $f(2)=3, f(3)=4, f(4)=f(5)=5$ and $g(3)=g(4)=7$ and $g(5)=g(9)=11$. Find $g \circ f$.

Solution We have $g \circ f(2)=g(f(2))=g(3)=7, g \circ f(3)=g(f(3))=g(4)=7$, $g \circ f(4)=g(f(4))=g(5)=11$ and $g \circ f(5)=g(5)=11$.

Example 16 Find $g$ of and $f \circ g$, if $f: \mathbf{R} \rightarrow \mathbf{R}$ and $g: \mathbf{R} \rightarrow \mathbf{R}$ are given by $f(x)=\cos x$ and $g(x)=3 x^{2}$. Show that $g \circ f \neq f \circ g$.

Solution We have $g \circ f(x)=g(f(x))=g(\cos x)=3(\cos x)^{2}=3 \cos ^{2} x$. Similarly, $f \circ g(x)=f(g(x))=f(3 x^{2})=\cos (3 x^{2})$. Note that $3 \cos ^{2} x \neq \cos 3 x^{2}$, for $x=0$. Hence, gof $\neq$ fog.

Definition 9 A function $f: X \rightarrow Y$ is defined to be invertible, if there exists a function $g: Y \rightarrow X$ such that $g \circ f=I_{X}$ and $f \circ g=I_{Y}$. The function $g$ is called the inverse of $f$ and is denoted by $f^{-1}$.

Thus, if $f$ is invertible, then $f$ must be one-one and onto and conversely, if $f$ is one-one and onto, then $f$ must be invertible. This fact significantly helps for proving a function $f$ to be invertible by showing that $f$ is one-one and onto, specially when the actual inverse of $f$ is not to be determined.

Example 17 Let $f: \mathbf{N} \rightarrow Y$ be a function defined as $f(x)=4 x+3$, where, $Y=\{y \in \mathbf{N}: y=4 x+3$ for some $x \in \mathbf{N}\}$. Show that $f$ is invertible. Find the inverse.

Solution Consider an arbitrary element $y$ of Y. By the definition of Y, $y=4 x+3$, for some $x$ in the domain $\mathbf{N}$. This shows that $x=\frac{(y-3)}{4}$. Define $g: Y \rightarrow \mathbf{N}$ by $g(y)=\frac{(y-3)}{4}$. Now, $g \circ f(x)=g(f(x))=g(4 x+3)=\frac{(4 x+3-3)}{4}=x$ and

$f \circ g(y)=f(g(y))=f(\frac{(y-3)}{4})=\frac{4(y-3)}{4}+3=y-3+3=y$. This shows that $g \circ f=I_{N}$ and $f o g=I_{Y}$, which implies that $f$ is invertible and $g$ is the inverse of $f$.

Miscellaneous Examples

Example 18 If $R_{1}$ and $R_{2}$ are equivalence relations in a set $A$, show that $R_{1} \cap R_{2}$ is also an equivalence relation.

Solution Since $R_{1}$ and $R_{2}$ are equivalence relations, $(a, a) \in R_{1}$, and $(a, a) \in R_{2} \forall a \in A$. This implies that $(a, a) \in R_{1} \cap R_{2}, \forall a$, showing $R_{1} \cap R_{2}$ is reflexive. Further, $(a, b) \in R_{1} \cap R_{2} \Rightarrow(a, b) \in R_{1}$ and $(a, b) \in R_{2} \Rightarrow(b, a) \in R_{1}$ and $(b, a) \in R_{2} \Rightarrow$ $(b, a) \in R_{1} \cap R_{2}$, hence, $R_{1} \cap R_{2}$ is symmetric. Similarly, $(a, b) \in R_{1} \cap R_{2}$ and $(b, c) \in R_{1} \cap R_{2} \Rightarrow(a, c) \in R_{1}$ and $(a, c) \in R_{2} \Rightarrow(a, c) \in R_{1} \cap R_{2}$. This shows that $R_{1} \cap R_{2}$ is transitive. Thus, $R_{1} \cap R_{2}$ is an equivalence relation.

Example 19 Let $R$ be a relation on the set $A$ of ordered pairs of positive integers defined by $(x, y) R(u, v)$ if and only if $x v=y u$. Show that $R$ is an equivalence relation.

Solution Clearly, $(x, y) R(x, y), \forall(x, y) \in A$, since $x y=y x$. This shows that $R$ is reflexive. Further, $(x, y) R(u, v) \Rightarrow x v=y u \Rightarrow u y=v x$ and hence $(u, v) R(x, y)$. This shows that $R$ is symmetric. Similarly, $(x, y) R(u, v)$ and $(u, v) R(a, b) \Rightarrow x v=y u$ and $u b=v a \Rightarrow x v \frac{a}{u}=y u \frac{a}{u} \Rightarrow x v \frac{b}{v}=y u \frac{a}{u} \Rightarrow x b=y a$ and hence $(x, y) R(a, b)$. Thus, $R$ is transitive. Thus, $R$ is an equivalence relation.

Example 20 Let $X=\{1,2,3,4,5,6,7,8,9\}$. Let $R_{1}$ be a relation in $X$ given by $R_{1}=\{(x, y): x-y$ is divisible by 3$\$ and $R_{2}$ be another relation on $X$ given by $R_{2}=\{(x, y):\{x, y\} \subset\{1,4,7\}\}$ or $\{x, y\} \subset\{2,5,8\}$ or $.\{x, y\} \subset\{3,6,9\}\}$. Show that $R_{1}=R_{2}$.

Solution Note that the characteristic of sets $\{1,4,7\},\{2,5,8\}$ and $\{3,6,9\}$ is that difference between any two elements of these sets is a multiple of 3 . Therefore, $(x, y) \in R_{1} \Rightarrow x-y$ is a multiple of $3 \Rightarrow\{x, y\} \subset\{1,4,7\}$ or $\{x, y\} \subset\{2,5,8\}$ or $\{x, y\} \subset\{3,6,9\} \Rightarrow(x, y) \in R_{2}$. Hence, $R_{1} \subset R_{2}$. Similarly, $\{x, y\} \in R_{2} \Rightarrow\{x, y\}$ $\subset\{1,4,7\}$ or $\{x, y\} \subset\{2,5,8\}$ or $\{x, y\} \subset\{3,6,9\} \Rightarrow x-y$ is divisible by $3 \Rightarrow\{x, y\} \in R_{1}$. This shows that $R_{2} \subset R_{1}$. Hence, $R_{1}=R_{2}$.

Example 21 Let $f: X \rightarrow Y$ be a function. Define a relation $R$ in $X$ given by $R=\{(a, b): f(a)=f(b)\}$. Examine whether $R$ is an equivalence relation or not.

Solution For every $a \in X,(a, a) \in R$, since $f(a)=f(a)$, showing that $R$ is reflexive. Similarly, $(a, b) \in R \Rightarrow f(a)=f(b) \Rightarrow f(b)=f(a) \Rightarrow(b, a) \in R$. Therefore, $R$ is symmetric. Further, $(a, b) \in R$ and $(b, c) \in R \Rightarrow f(a)=f(b)$ and $f(b)=f(c) \Rightarrow f(a)$ $=f(c) \Rightarrow(a, c) \in R$, which implies that $R$ is transitive. Hence, $R$ is an equivalence relation.

Example 22 Find the number of all one-one functions from set $A=\{1,2,3\}$ to itself.

Solution One-one function from $\{1,2,3\}$ to itself is simply a permutation on three symbols $1,2,3$. Therefore, total number of one-one maps from $\{1,2,3\}$ to itself is same as total number of permutations on three symbols $1,2,3$ which is $3 !=6$.

Example 23 Let $A=\{1,2,3\}$. Then show that the number of relations containing $(1,2)$ and $(2,3)$ which are reflexive and transitive but not symmetric is three.

Solution The smallest relation $R_{1}$ containing $(1,2)$ and $(2,3)$ which is reflexive and transitive but not symmetric is $\{(1,1),(2,2),(3,3),(1,2),(2,3),(1,3)\}$. Now, if we add the pair $(2,1)$ to $R_{1}$ to get $R_{2}$, then the relation $R_{2}$ will be reflexive, transitive but not symmetric. Similarly, we can obtain $R_{3}$ by adding $(3,2)$ to $R_{1}$ to get the desired relation. However, we can not add two pairs $(2,1),(3,2)$ or single pair $(3,1)$ to $R_{1}$ at a time, as by doing so, we will be forced to add the remaining pair in order to maintain transitivity and in the process, the relation will become symmetric also which is not required. Thus, the total number of desired relations is three.

Example 24 Show that the number of equivalence relation in the set $\{1,2,3\}$ containing $(1,2)$ and $(2,1)$ is two.

Solution The smallest equivalence relation $R_{1}$ containing $(1,2)$ and $(2,1)$ is $\{(1,1)$, $(2,2),(3,3),(1,2),(2,1)\}$. Now we are left with only 4 pairs namely $(2,3),(3,2)$, $(1,3)$ and $(3,1)$. If we add any one, say $(2,3)$ to $R_{1}$, then for symmetry we must add $(3,2)$ also and now for transitivity we are forced to add $(1,3)$ and $(3,1)$. Thus, the only equivalence relation bigger than $R_{1}$ is the universal relation. This shows that the total number of equivalence relations containing $(1,2)$ and $(2,1)$ is two.

Example 25 Consider the identity function $I_{\mathbf{N}}: \mathbf{N} \rightarrow \mathbf{N}$ defined as $I_{\mathbf{N}}(x)=x \forall x \in \mathbf{N}$. Show that although $I_{\mathbf{N}}$ is onto but $I_{\mathbf{N}}+I_{\mathbf{N}}: \mathbf{N} \rightarrow \mathbf{N}$ defined as

$$ (I_{N}+I_{N})(x)=I_{N}(x)+I_{N}(x)=x+x=2 x \text { is not onto. } $$

Solution Clearly $I_{N}$ is onto. But $I_{N}+I_{N}$ is not onto, as we can find an element 3 in the co-domain $\mathbf{N}$ such that there does not exist any $x$ in the domain $\mathbf{N}$ with $(I_{N}+I_{N})(x)=2 x=3$.

Example 26 Consider a function $f:[0, \frac{\pi}{2}] \rightarrow \mathbf{R}$ given by $f(x)=\sin x$ and $g:[0, \frac{\pi}{2}] \rightarrow \mathbf{R}$ given by $g(x)=\cos x$. Show that $f$ and $g$ are one-one, but $f+g$ is not one-one.

Solution Since for any two distinct elements $x_{1}$ and $x_{2}$ in $[0, \frac{\pi}{2}], \sin x_{1} \neq \sin x_{2}$ and $\cos x_{1} \neq \cos x_{2}$, both $f$ and $g$ must be one-one. But $(f+g)(0)=\sin 0+\cos 0=1$ and $(f+g)(\frac{\pi}{2})=\sin \frac{\pi}{2}+\cos \frac{\pi}{2}=1$. Therefore, $f+g$ is not one-one.

Miscellaneous Exercise on Chapter 1

1. Show that the function $f: \mathbf{R} \rightarrow\{x \in \mathbf{R}:-1<x<1\}$ defined by $f(x)=\frac{x}{1+|x|}$, $x \in \mathbf{R}$ is one one and onto function.

Solution

It is given that $f: \mathbf{R} \to{x \in \mathbf{R}:-1<x<1}$ is defined as $f(x)=\frac{x}{1+|x|}, x \in \mathbf{R}$.

Suppose $f(x)=f(y)$, where $x, y \in \mathbf{R}$.

$ \Rightarrow \frac{x}{1+|x|}=\frac{y}{1+|y|} $

It can be observed that if $x$ is positive and $y$ is negative, then we have:

$ \frac{x}{1+x}=\frac{y}{1-y} \Rightarrow 2 x y=x-y $

Since $x$ is positive and $y$ is negative:

$x>y \Rightarrow x-y>0$

But, $2 x y$ is negative.

Then, $2 x y \neq x-y$.

Thus, the case of $x$ being positive and $y$ being negative can be ruled out.

Under a similar argument, $x$ being negative and $y$ being positive can also be ruled out $\therefore x$ and $y$ have to be either positive or negative.

When $x$ and $y$ are both positive, we have:

$ f(x)=f(y) \Rightarrow \frac{x}{1+x}=\frac{y}{1+y} \Rightarrow x+x y=y+x y \Rightarrow x=y $

When $x$ and $y$ are both negative, we have:

$ f(x)=f(y) \Rightarrow \frac{x}{1-x}=\frac{y}{1-y} \Rightarrow x-x y=y-y x \Rightarrow x=y $

$\therefore f$ is one-one.

Now, let $y \in \mathbf{R}$ such that $-1<y<1$.

If $y$ is negative, then there exists $x=\frac{y}{1+v} \in \mathbf{R}$ such that

$f(x)=f(\frac{y}{1+y})=\frac{(\frac{y}{1+y})}{1+|\frac{y}{1+y}|}=\frac{\frac{y}{1+y}}{1+(\frac{-y}{1+y})}=\frac{y}{1+y-y}=y$.

If $y$ is positive, then there exists $x=\frac{y}{1-y} \in \mathbf{R}$ such that

$ f(x)=f(\frac{y}{1-y})=\frac{(\frac{y}{1-y})}{1+|(\frac{y}{1-y})|}=\frac{\frac{y}{1-y}}{1+\frac{y}{1-y}}=\frac{y}{1-y+y}=y . $

$\therefore f$ is onto.

Hence, $f$ is one-one and onto.

2. Show that the function $f: \mathbf{R} \rightarrow \mathbf{R}$ given by $f(x)=x^{3}$ is injective.

Solution

$f: \mathbf{R} \to \mathbf{R}$ is given as $f(x)=x^{3}$.

Suppose $f(x)=f(y)$, where $x, y \in \mathbf{R}$.

$\Rightarrow x^{3}=y^{3}$

Now, we need to show that $x=y$.

Suppose $x \neq y$, their cubes will also not be equal.

$\Rightarrow x^{3} \neq y^{3}$

However, this will be a contradiction to (1).

$\therefore x=y$

Hence, $f$ is injective.

3. Given a non empty set $X$, consider $P(X)$ which is the set of all subsets of $X$. Define the relation $R$ in $P(X)$ as follows:

For subsets $A, B$ in $P(X), ARB$ if and only if $A \subset B$. Is $R$ an equivalence relation on $P(X)$ ? Justify your answer.

Solution

Since every set is a subset of itself, $A R A$ for all $A \in P(X)$.

$\therefore R$ is reflexive.

Let $A R B \Rightarrow A \subset B$.

This cannot be implied to $B \subset A$.

For instance, if $A={1,2}$ and $B={1,2,3}$, then it cannot be implied that $B$ is related to $A$.

$\therefore R$ is not symmetric.

Further, if $A R B$ and $B R C$, then $A \subset B$ and $B \subset C$.

$\Rightarrow A \subset C$

$\Rightarrow A R C$

$\therefore R$ is transitive.

Hence, $R$ is not an equivalence relation since it is not symmetric.

4. Find the number of all onto functions from the set $\{1,2,3, \ldots \ldots, n\}$ to itself.

Solution

Onto functions from the set ${1,2,3, \ldots, n}$ to itself is simply a permutation on $n$ symbols $1,2, \ldots, n$.

Thus, the total number of onto maps from ${1,2, \ldots, n}$ to itself is the same as the total number of permutations on $n$ symbols $1,2, \ldots, n$, which is $n$.

5. Let $A=\{-1,0,1,2\}, B=\{-4,-2,0,2\}$ and $f, g: A \rightarrow B$ be functions defined by $f(x)=x^{2}-x, x \in A$ and $g(x)=2|x-\frac{1}{2}|-1, x \in A$. Are $f$ and $g$ equal? Justify your answer. (Hint: One may note that two functions $f: A \rightarrow B$ and $g: A \rightarrow B$ such that $f(a)=g(a) \forall a \in A$, are called equal functions).

Solution

It is given that $A={-1,0,1,2}, B={-4,-2,0,2}$.

Also, it is given that $f, g: A \to B$ are defined by $f(x)=x^{2}-x, x \in A$ and

$ g(x)=2|x-\frac{1}{2}|-1, x \in A $

It is observed that:

$ \begin{aligned} & f(-1)=(-1)^{2}-(-1)=1+1=2 \\ & g(-1)=2|(-1)-\frac{1}{2}|-1=2(\frac{3}{2})-1=3-1=2 \\ & \Rightarrow f(-1)=g(-1) \\ & f(0)=(0)^{2}-0=0 \\ & g(0)=2|0-\frac{1}{2}|-1=2(\frac{1}{2})-1=1-1=0 \\ & \Rightarrow f(0)=g(0) \\ & f(1)=(1)^{2}-1=1-1=0 \\ & g(1)=2|1-\frac{1}{2}|-1=2(\frac{1}{2})-1=1-1=0 \\ & \Rightarrow f(1)=g(1) \\ & f(2)=(2)^{2}-2=4-2=2 \\ & g(2)=2|2-\frac{1}{2}|-1=2(\frac{3}{2})-1=3-1=2 \\ & \Rightarrow f(2)=g(2) \\ & \therefore f(a)=g(a) \forall a \in A \end{aligned} $

Hence, the functions $f$ and $g$ are equal.

6. Let $A=\{1,2,3\}$. Then number of relations containing $(1,2)$ and $(1,3)$ which are reflexive and symmetric but not transitive is

(A) 1

(B) 2

(C) 3

(D) 4

Solution

The given set is $A={1,2,3}$.

The smallest relation containing $(1,2)$ and $(1,3)$ which is reflexive and symmetric, but not transitive is given by: $R={(1,1),(2,2),(3,3),(1,2),(1,3),(2,1),(3,1)}$

This is because relation $R$ is reflexive as $(1,1),(2,2),(3,3) \in R$.

Relation $R$ is symmetric since $(1,2),(2,1) \in R$ and $(1,3),(3,1) \in R$.

But relation $R$ is not transitive as $(3,1),(1,2) \in R$, but $(3,2) \notin R$.

Now, if we add any two pairs $(3,2)$ and $(2,3)$ (or both) to relation $R$, then relation $R$ will become transitive.

Hence, the total number of desired relations is one.

The correct answer is A.

7. Let $A=\{1,2,3\}$. Then number of equivalence relations containing $(1,2)$ is

(A) 1

(B) 2

(C) 3

(D) 4

Solution

It is given that $A={1,2,3}$.

The smallest equivalence relation containing $(1,2)$ is given by,

$R_1={(1,1),(2,2),(3,3),(1,2),(2,1)}$

Now, we are left with only four pairs i.e., $(2,3),(3,2),(1,3)$, and $(3,1)$.

If we odd any one pair [say $(2,3)$ ] to $R_1$, then for symmetry we must add $(3,2)$. Also, for transitivity we are required to add $(1,3)$ and $(3,1)$.

Hence, the only equivalence relation (bigger than $R_1$ ) is the universal relation.

This shows that the total number of equivalence relations containing $(1,2)$ is two.

The correct answer is B.

Summary

In this chapter, we studied different types of relations and equivalence relation, composition of functions, invertible functions and binary operations. The main features of this chapter are as follows:

Empty relation is the relation $R$ in $X$ given by $R=\phi \subset X \times X$.

• Universal relation is the relation $R$ in $X$ given by $R=X \times X$.

• Reflexive relation $R$ in $X$ is a relation with $(a, a) \in R \forall a \in X$.

• Symmetric relation $R$ in $X$ is a relation satisfying $(a, b) \in R$ implies $(b, a) \in R$.

• Transitive relation $R$ in $X$ is a relation satisfying $(a, b) \in R$ and $(b, c) \in R$ implies that $(a, c) \in R$.

• Equivalence relation $R$ in $X$ is a relation which is reflexive, symmetric and transitive.

• Equivalence class $[a]$ containing $a \in X$ for an equivalence relation $R$ in $X$ is the subset of $X$ containing all elements $b$ related to $a$.

• A function $f: X \rightarrow Y$ is one-one (or injective) if $f(x_{1})=f(x_{2}) \Rightarrow x_{1}=x_{2} \forall x_{1}, x_{2} \in X$.

• A function $f: X \rightarrow Y$ is onto (or surjective) if given any $y \in Y, \exists x \in X$ such that $f(x)=y$.

A function $f: X \rightarrow Y$ is one-one and onto (or bijective), if $f$ is both one-one and onto.

• Given a finite set $X$, a function $f: X \rightarrow X$ is one-one (respectively onto) if and only if $f$ is onto (respectively one-one). This is the characteristic property of a finite set. This is not true for infinite set

Historical Note

The concept of function has evolved over a long period of time starting from R. Descartes (1596-1650), who used the word ‘function’ in his manuscript “Geometrie” in 1637 to mean some positive integral power $x^{n}$ of a variable $x$ while studying geometrical curves like hyperbola, parabola and ellipse. James Gregory (1636-1675) in his work " Vera Circuli et Hyperbolae Quadratura" (1667) considered function as a quantity obtained from other quantities by successive use of algebraic operations or by any other operations. Later G. W. Leibnitz (1646-1716) in his manuscript “Methodus tangentium inversa, seu de functionibus” written in 1673 used the word ‘function’ to mean a quantity varying from point to point on a curve such as the coordinates of a point on the curve, the slope of the curve, the tangent and the normal to the curve at a point. However, in his manuscript “Historia” (1714), Leibnitz used the word ‘function’ to mean quantities that depend on a variable. He was the first to use the phrase ‘function of $x^{\prime}$. John Bernoulli (1667-1748) used the notation $\phi x$ for the first time in 1718 to indicate a function of $x$. But the general adoption of symbols like $f, F, \phi, \psi \ldots$ to represent functions was made by Leonhard Euler (1707-1783) in 1734 in the first part of his manuscript “Analysis Infinitorium”. Later on, Joeph Louis Lagrange (1736-1813) published his manuscripts “Theorie des functions analytiques” in 1793, where he discussed about analytic function and used the notion $f(x), F(x)$, $\phi(x)$ etc. for different function of $x$. Subsequently, Lejeunne Dirichlet (1805-1859) gave the definition of function which was being used till the set theoretic definition of function presently used, was given after set theory was developed by Georg Cantor (1845-1918). The set theoretic definition of function known to us presently is simply an abstraction of the definition given by Dirichlet in a rigorous manner.