PROBABILITY

The theory of probabilities is simply the Science of logic

quantitatively treated. - C.S. PEIRCE

Introduction

In earlier Classes, we have studied the probability as a measure of uncertainty of events in a random experiment. We discussed the axiomatic approach formulated by Russian Mathematician, A.N. Kolmogorov (1903-1987) and treated probability as a function of outcomes of the experiment. We have also established equivalence between the axiomatic theory and the classical theory of probability in case of equally likely outcomes. On the basis of this relationship, we obtained probabilities of events associated with discrete sample spaces. We have also studied the addition rule of probability. In this chapter, we shall discuss the important concept of conditional probability of an event given that another event has occurred, which will be helpful in understanding the Bayes’ theorem, multiplication rule of probability and independence of events. We shall also learn

Pierre de Fermat $(1601-1665)$ an important concept of random variable and its probability distribution and also the mean and variance of a probability distribution. In the last section of the chapter, we shall study an important discrete probability distribution called Binomial distribution. Throughout this chapter, we shall take up the experiments having equally likely outcomes, unless stated otherwise.

Conditional Probability

Uptill now in probability, we have discussed the methods of finding the probability of events. If we have two events from the same sample space, does the information about the occurrence of one of the events affect the probability of the other event? Let us try to answer this question by taking up a random experiment in which the outcomes are equally likely to occur.

Consider the experiment of tossing three fair coins. The sample space of the experiment is

$ S={HHH, HHT, HTH, THH, HTT, THT, TTH, TTT} $

Since the coins are fair, we can assign the probability $\frac{1}{8}$ to each sample point. Let $E$ be the event ‘at least two heads appear’ and $F$ be the event ‘first coin shows tail’. Then

Now, suppose we are given that the first coin shows tail, i.e. F occurs, then what is the probability of occurrence of $E$ ? With the information of occurrence of $F$, we are sure that the cases in which first coin does not result into a tail should not be considered while finding the probability of $E$. This information reduces our sample space from the set $S$ to its subset $F$ for the event $E$. In other words, the additional information really amounts to telling us that the situation may be considered as being that of a new random experiment for which the sample space consists of all those outcomes only which are favourable to the occurrence of the event $F$.

Now, the sample point of $F$ which is favourable to event $E$ is THH.

Thus, Probability of $E$ considering $F$ as the sample space $=\frac{1}{4}$,

or $\quad$ Probability of $E$ given that the event $F$ has occurred $=\frac{1}{4}$

This probability of the event $E$ is called the conditional probability of $E$ given that $F$ has already occurred, and is denoted by $P(E \mid F)$.

Thus $\quad P(E \mid F)=\frac{1}{4}$

Note that the elements of $F$ which favour the event $E$ are the common elements of $E$ and $F$, i.e. the sample points of $E \cap F$.

Thus, we can also write the conditional probability of $E$ given that $F$ has occurred as

$ \begin{aligned} P(E \mid F) & =\frac{\text{ Number of elementary events favourable to } E \cap F}{\text{ Number of elementary events which are favourable to } F} \\ & =\frac{n(E \cap F)}{n(F)} \end{aligned} $

Dividing the numerator and the denominator by total number of elementary events of the sample space, we see that $P(EIF)$ can also be written as

$ P(E \mid F)=\frac{\frac{n(E \cap F)}{n(S)}}{\frac{n(F)}{n(S)}}=\frac{P(E \cap F)}{P(F)} $

Note that (1) is valid only when $P(F) \neq 0$ i.e., $F \neq \phi$ (Why?)

Thus, we can define the conditional probability as follows :

Definition 1

If $E$ and $F$ are two events associated with the same sample space of a random experiment, the conditional probability of the event $E$ given that $F$ has occurred, i.e. $P(E \mid F)$ is given by

$ P(EIF)=\frac{P(E \cap F)}{P(F)} \text{ provided } P(F) \neq 0 $

Properties of conditional probability

Let $E$ and $F$ be events of a sample space $S$ of an experiment, then we have Property $1 P(S \mid F)=P(F \mid F)=1$

We know that

Also

$ \begin{aligned} & P(S \mid F)=\frac{P(S \cap F)}{P(F)}=\frac{P(F)}{P(F)}=1 \\ & P(F \mid F)=\frac{P(F \cap F)}{P(F)}=\frac{P(F)}{P(F)}=1 \\ & P(S \mid F)=P(F \mid F)=1 \end{aligned} $

Thus

Property 2 If $A$ and $B$ are any two events of a sample space $S$ and $F$ is an event of $S$ such that $P(F) \neq 0$, then

$ P((A \cup B) \mid F)=P(A \mid F)+P(B \mid F)-P((A \cap B) \mid F) $

In particular, if $A$ and $B$ are disjoint events, then

We have

$ P((A \cup B) \mid F)=P(A \mid F)+P(B \mid F) $

$ \begin{aligned} P((A \cup B) \mid F) & =\frac{P[(A \cup B) \cap F]}{P(F)} \\ & =\frac{P[(A \cap F) \cup(B \cap F)]}{P(F)} \end{aligned} $

(by distributive law of union of sets over intersection)

$ \begin{aligned} & =\frac{P(A \cap F)+P(B \cap F)-P(A \cap B \cap F)}{P(F)} \\ & =\frac{P(A \cap F)}{P(F)}+\frac{P(B \cap F)}{P(F)}-\frac{P[(A \cap B) \cap F]}{P(F)} \\ & =P(A \mid F)+P(B \mid F)-P((A \cap B) \mid F) \end{aligned} $

When $A$ and $B$ are disjoint events, then

$ \begin{matrix}
& P((A \cap B) \mid F)=0 \\ \Rightarrow \quad & P((A \cup B) \mid F)=P(A \mid F)+P(B \mid F) \end{matrix} $

Property $3 P(E^{\prime} \mid F)=1-P(E \mid F)$

From Property 1 , we know that $P(SIF)=1$

$ \begin{matrix} \Rightarrow & P(E \cup E^{\prime} \mid F)=1 & \text{ since } S=E \cup E^{\prime} \\ \Rightarrow & P(E \mid F)+P(E^{\prime} \mid F)=1 & \text{ since } E \text{ and } E^{\prime} \text{ are disjoint events } \\ \text{ Thus, } & P(E^{\prime} \mid F)=1-P(E \mid F) & \end{matrix} $

Let us now take up some examples.

Example 1 If $P(A)=\frac{7}{13}, P(B)=\frac{9}{13}$ and $P(A \cap B)=\frac{4}{13}$, evaluate $P(A \mid B)$.

Solution We have $P(A \mid B)=\frac{P(A \cap B)}{P(B)}=\frac{\frac{4}{13}}{\frac{9}{13}}=\frac{4}{9}$

Example 2 A family has two children. What is the probability that both the children are boys given that at least one of them is a boy?

Solution Let $b$ stand for boy and $g$ for girl. The sample space of the experiment is

$ S={(b, b),(g, b),(b, g),(g, g)} $

Let $E$ and $F$ denote the following events :

E : ‘both the children are boys’

$F$ : ‘at least one of the child is a boy’

Then

$E={(b, b)}$ and $F={(b, b),(g, b),(b, g)}$

Now

$E \cap F={(b, b)}$

Thus

$ P(F)=\frac{3}{4} \text{ and } P(E \cap F)=\frac{1}{4} $

Therefore

$ P(E \mid F)=\frac{P(E \cap F)}{P(F)}=\frac{\frac{1}{4}}{\frac{3}{4}}=\frac{1}{3} $

Example 3 Ten cards numbered 1 to 10 are placed in a box, mixed up thoroughly and then one card is drawn randomly. If it is known that the number on the drawn card is more than 3 , what is the probability that it is an even number?

Solution Let A be the event ’the number on the card drawn is even’ and B be the event ’the number on the card drawn is greater than 3 ‘. We have to find $P(AlB)$.

Now, the sample space of the experiment is $S={1,2,3,4,5,6,7,8,9,10}$

Then

$ A={2,4,6,8,10}, B={4,5,6,7,8,9,10} $

and

$ A \cap B={4,6,8,10} $

Also

$ P(A)=\frac{5}{10}, P(B)=\frac{7}{10} \text{ and } P(A \cap B)=\frac{4}{10} $

Then

$ P(A \mid B)=\frac{P(A \cap B)}{P(B)}=\frac{\frac{4}{10}}{\frac{7}{10}}=\frac{4}{7} $

Example 4 In a school, there are 1000 students, out of which 430 are girls. It is known that out of $430,10 %$ of the girls study in class XII. What is the probability that a student chosen randomly studies in Class XII given that the chosen student is a girl?

Solution Let E denote the event that a student chosen randomly studies in Class XII and $F$ be the event that the randomly chosen student is a girl. We have to find $P(EIF)$.

Now $\quad P(F)=\frac{430}{1000}=0.43$ and $P(E \cap F)=\frac{43}{1000}=0.043$ (Why?)

Then $\quad P(E \mid F)=\frac{P(E \cap F)}{P(F)}=\frac{0.043}{0.43}=0.1$

Example 5 A die is thrown three times. Events A and B are defined as below:

A : 4 on the third throw

B : 6 on the first and 5 on the second throw

Find the probability of A given that B has already occurred.

Solution The sample space has 216 outcomes.

Now

$ \begin{aligned} & B={(6,5,1),(6,5,2),(6,5,3),(6,5,4),(6,5,5),(6,5,6)} \end{aligned} $

and

$ A \cap B={(6,5,4)} . $

Now

$ P(B)=\frac{6}{216} \text{ and } P(A \cap B)=\frac{1}{216} $

Then

$ P(A \mid B)=\frac{P(A \cap B)}{P(B)}=\frac{\frac{1}{216}}{\frac{6}{216}}=\frac{1}{6} $

Example 6 A die is thrown twice and the sum of the numbers appearing is observed to be 6 . What is the conditional probability that the number 4 has appeared at least once?

Solution Let $E$ be the event that ’number 4 appears at least once’ and $F$ be the event that ’the sum of the numbers appearing is 6 ‘.

Then,

$ \begin{aligned} & E={(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(1,4),(2,4),(3,4),(5,4),(6,4)} \\ & F={(1,5),(2,4),(3,3),(4,2),(5,1)} \end{aligned} $

and

We have

$ P(E)=\frac{11}{36} \text{ and } P(F)=\frac{5}{36} $

Also

$ E \cap F={(2,4),(4,2)} $

Therefore

$ P(E \cap F)=\frac{2}{36} $

Hence, the required probability

$ P(E \mid F)=\frac{P(E \cap F)}{P(F)}=\frac{\frac{2}{36}}{\frac{5}{36}}=\frac{2}{5} $

For the conditional probability discussed above, we have considered the elementary events of the experiment to be equally likely and the corresponding definition of the probability of an event was used. However, the same definition can also be used in the general case where the elementary events of the sample space are not equally likely, the probabilities $P(E \cap F)$ and $P(F)$ being calculated accordingly. Let us take up the following example.

Example 7 Consider the experiment of tossing a coin. If the coin shows head, toss it again but if it shows tail, then throw a die. Find the conditional probability of the event that ’the die shows a number greater than 4 ’ given that ’there is at least one tail’.

Solution The outcomes of the experiment can be represented in following diagrammatic manner called the ’tree diagram’.

The sample space of the experiment may be described as

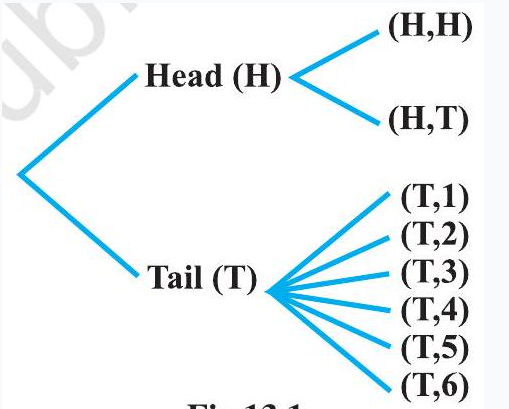
Fig 13.1

$ S={(H, H),(H, T),(T, 1),(T, 2),(T, 3),(T, 4),(T, 5),(T, 6)} $

where $(H, H)$ denotes that both the tosses result into head and $(T, i)$ denote the first toss result into a tail and the number $i$ appeared on the die for $i=1,2,3,4,5,6$. Thus, the probabilities assigned to the 8 elementary events

$(H, H),(H, T),(T, 1),(T, 2),(T, 3)(T, 4),(T, 5),(T, 6)$ are $\frac{1}{4}, \frac{1}{4}, \frac{1}{12}, \frac{1}{12}, \frac{1}{12}, \frac{1}{12}, \frac{1}{12}, \frac{1}{12}$ respectively which is clear from the Fig 13.2.

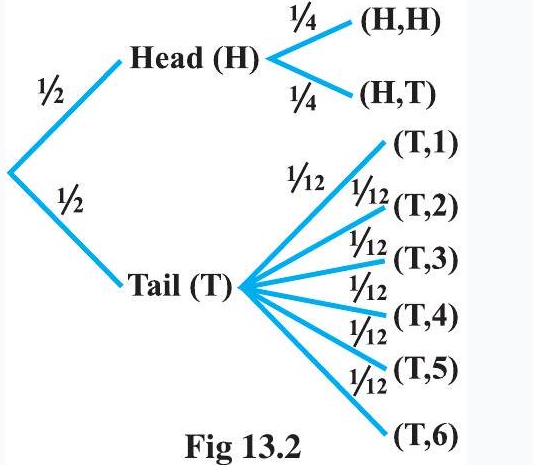
Let $F$ be the event that ’there is at least one tail’ and $E$ be the event ’the die shows a number greater than 4 ‘. Then

$ \begin{aligned} & F={(H, T),(T, 1),(T, 2),(T, 3),(T, 4),(T, 5),(T, 6)} \\ & E={(T, 5),(T, 6)} \text{ and } E \cap F={(T, 5),(T, 6)} \end{aligned} $

Now

$ \begin{aligned} P(F)= & P({(H, T)})+P({(T, 1)})+P({(T, 2)})+P({(T, 3)}) \\ & +P({(T, 4)})+P({(T, 5)})+P({(T, 6)}) \\ = & \frac{1}{4}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}=\frac{3}{4} \end{aligned} $

and $\quad P(E \cap F)=P({(T, 5)})+P({(T, 6)})=\frac{1}{12}+\frac{1}{12}=\frac{1}{6}$

Hence $\quad P(E \mid F)=\frac{P(E \cap F)}{P(F)}=\frac{\frac{1}{6}}{\frac{3}{4}}=\frac{2}{9}$

EXERCISE 13.1

1. Given that $E$ and $F$ are events such that $P(E)=0.6, P(F)=0.3$ and $P(E \cap F)=0.2$, find $P(E \mid F)$ and $P(F \mid E)$

Solution

It is given that $P(E)=0.6, P(F)=0.3$, and $P(E \cap F)=0.2$

$\Rightarrow P(E \mid F)=\frac{P(E \cap F)}{P(F)}=\frac{0.2}{0.3}=\frac{2}{3}$

$\Rightarrow P(F \mid E)=\frac{P(E \cap F)}{P(E)}=\frac{0.2}{0.6}=\frac{1}{3}$

2. Compute $P(A \mid B)$, if $P(B)=0.5$ and $P(A \cap B)=0.32$

Solution

It is given that $P(B)=0.5$ and $P(A \cap B)=0.32$

$\Rightarrow P(\frac{A}{B})=\frac{P(A \cap B)}{P(B)}=\frac{0.32}{0.5}=\frac{16}{25}$

3. If $P(A)=0.8, P(B)=0.5$ and $P(B \mid A)=0.4$, find

(i) $P(A \cap B)$

(ii) $P(A \mid B)$

(iii) $P(A \cup B)$

Solution

It is given that $P(A)=0.8, P(B)=0.5$, and $P(B \mid A)=0.4$

(i) $P(B \mid A)=0.4$

$\therefore \frac{P(A \cap B)}{P(A)}=0.4$

$\Rightarrow \frac{P(A \cap B)}{0.8}=0.4$

$\Rightarrow P(A \cap B)=0.32$

(ii) $P(A \mid B)=\frac{P(A \cap B)}{P(B)}$

$\Rightarrow P(A \mid B)=\frac{0.32}{0.5}=0.64$

(iii) $P(A \cup B)=P(A)+P(B)-P(A \cap B)$

$\Rightarrow P(A \cup B)=0.5+0.5-0.32=0.98$

4. Evaluate $P(A \cup B)$, if $2 P(A)=P(B)=\frac{5}{13}$ and $P(A \mid B)=\frac{2}{5}$

Solution

It is given that, $2 P(A)=P(B)=\frac{5}{13}$

$\Rightarrow P(A)=\frac{5}{26}$ and $P(B)=\frac{5}{13}$

$P(A \mid B)=\frac{2}{5}$

$\Rightarrow \frac{P(A \cap B)}{P(B)}=\frac{2}{5}$

$\Rightarrow P(A \cap B)=\frac{2}{5} \times P(B)=\frac{2}{5} \times \frac{5}{13}=\frac{2}{13}$

It is known that, $P(A \cup B)=P(A)+P(B)-P(A \cap B)$ $\Rightarrow P(A \cup B)=\frac{5}{26}+\frac{5}{13}-\frac{2}{13}$

$\Rightarrow P(A \cup B)=\frac{5+10-4}{26}$

$\Rightarrow P(A \cup B)=\frac{11}{26}$

5. If $P(A)=\frac{6}{11}, P(B)=\frac{5}{11}$ and $P(A \cup B)=\frac{7}{11}$, find

(i) $P(A \cap B)$

(ii) $P(A \mid B)$

(iii) $P(B \mid A)$

Solution

It is given that $P(A)=\frac{6}{11}, P(B)=\frac{5}{11}$, and $P(A \cup B)=\frac{7}{11}$

(i) $P(A \cup B)=\frac{7}{11}$

$\therefore P(A)+P(B)-P(A \cap B)=\frac{7}{11}$

$\Rightarrow \frac{6}{11}+\frac{5}{11}-P(A \cap B)=\frac{7}{11}$

$\Rightarrow P(A \cap B)=\frac{11}{11}-\frac{7}{11}=\frac{4}{11}$

(ii) It is known that, $P(A \mid B)=\frac{P(A \cap B)}{P(B)}$

$\Rightarrow P(A \mid B)=\frac{\frac{4}{11}}{\frac{5}{11}}=\frac{4}{5}$

(iii) It is known that, $P(B \mid A)=\frac{P(A \cap B)}{P(A)}$

$ \Rightarrow P(B \mid A)=\frac{\frac{4}{11}}{\frac{6}{11}}=\frac{4}{6}=\frac{2}{3} $

Determine $P(E \mid F)$ in Exercises 6 to 9.

6. A coin is tossed three times, where

(i) $E$ : head on third toss , $F$ : heads on first two tosses

(ii) $E$ : at least two heads, $F$ : at most two heads

(iii) $E$ : at most two tails , $F$ : at least one tail

Solution

If a coin is tossed three times, then the sample space $S$ is

$S={H H H, H H T, H T H, H T T, T H H, T H T, T T H, ~ T T T}$

It can be seen that the sample space has 8 elements.

(i) $E={HHH, HTH, THH, TTH}$

$F={HHH, HHT}$

$\therefore E \cap F={HHH}$

$P(F)=\frac{2}{8}=\frac{1}{4}$ and $P(E \cap F)=\frac{1}{8}$

$P(E \mid F)=\frac{P(E \cap F)}{P(F)}=\frac{\frac{1}{8}}{\frac{1}{4}}=\frac{4}{8}=\frac{1}{2}$

(ii) $E={HHH, HHT, HTH, THH}$

$F={H H T, H T H, H T T, T H H, T H T, T T H, T T T}$

$\therefore E \cap F={HHT, HTH, THH}$

Clearly, $P(E \cap F)=\frac{3}{8}$ and $P(F)=\frac{7}{8}$

$P(E \mid F)=\frac{P(E \cap F)}{P(F)}=\frac{\frac{3}{8}}{\frac{7}{8}}=\frac{3}{7}$

(iii) $E={HHH, HHT, HTT, HTH, THH, THT, TTH}$

$F={HHT, HTT, HTH, THH, THT, TTH, TTT}$ $\therefore E \cap F={HHT, HTT, HTH, THH, THT, TTH}$

$P(F)=\frac{7}{8}$ and $P(E \cap F)=\frac{6}{8}$

Therefore, $P(E \mid F)=\frac{P(E \cap F)}{P(F)}=\frac{\frac{6}{7}}{\frac{7}{8}}=\frac{6}{7}$

7. Two coins are tossed once, where

(i) $E$ : tail appears on one coin, $\quad F$ : one coin shows head

(ii) E : no tail appears, F : no head appears

Solution

If two coins are tossed once, then the sample space $S$ is

$S={HH, HT, TH, TT}$

(i) $E={HT, TH}$

$F={HT, TH}$

$\therefore E \cap F={HT, TH}$

$P(F)=\frac{2}{8}=\frac{1}{4}$

$P(E \cap F)=\frac{2}{8}=\frac{1}{4}$

$\therefore P(E \mid F)=\frac{P(E \cap F)}{P(F)}=\frac{2}{2}=1$

(ii) $E={HH}$

$F={TT}$

$\therefore E \cap F=\Phi$

$P(F)=1$ and $P(E \cap F)=0$ $\therefore P(E \mid F)=\frac{P(E \cap F)}{P(F)}=\frac{0}{1}=0$

8. A die is thrown three times, E : 4 appears on the third toss, F : 6 and 5 appears respectively on first two tosses

Solution

If a die is thrown three times, then the number of elements in the sample space will be 6 $\times 6 \times 6=216$

$E=\begin{bmatrix} (1,1,4),(1,2,4), \ldots(1,6,4) \\ (2,1,4),(2,2,4), \ldots(2,6,4) \\ (3,1,4),(3,2,4), \ldots(3,6,4) \\ (4,1,4),(4,2,4), \ldots(4,6,4) \\ (5,1,4),(5,2,4), \ldots(5,6,4) \\ (6,1,4),(6,2,4), \ldots(6,6,4) \end{bmatrix} $

$F={(6,5,1),(6,5,2),(6,5,3),(6,5,4),(6,5,5),(6,5,6)}$

$\therefore E \cap F={(6,5,4)}$

$P(F)=\frac{6}{216}$ and $P(E \cap F)=\frac{1}{216}$

$\therefore P(E \mid F)=\frac{P(E \cap F)}{P(F)}=\frac{\frac{1}{216}}{\frac{6}{216}}=\frac{1}{6}$

9. Mother, father and son line up at random for a family picture E : son on one end, $F$ : father in middle

Solution

If mother (M), father (F), and son (S) line up for the family picture, then the sample space will be

$S={M F S, M S F, F M S, F S M, S M F, S F M}$

$\Rightarrow E={MFS, FMS, SMF, SFM}$

$F={M F S, S F M}$

$\therefore E \cap F={MFS, SFM}$

$P(E \cap F)=\frac{2}{6}=\frac{1}{3}$

$P(F)=\frac{2}{6}=\frac{1}{3}$

$\therefore P(E \mid F)=\frac{P(E \cap F)}{P(F)}=\frac{\frac{1}{3}}{\frac{1}{3}}=1$

10. A black and a red dice are rolled.

(a) Find the conditional probability of obtaining a sum greater than 9 , given that the black die resulted in a 5 .

(b) Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4.

Solution

Let the first observation be from the black die and second from the red die.

When two dice (one black and another red) are rolled, the sample space $S$ has $6 \times 6=$ 36 number of elements.

1. Let

A: Obtaining a sum greater than 9

$={(4,6),(5,5),(5,6),(6,4),(6,5),(6,6)}$

B: Black die results in a 5 .

$={(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)}$

$\therefore A \cap B={(5,5),(5,6)}$

The conditional probability of obtaining a sum greater than 9, given that the black die resulted in a 5 , is given by $P(A \mid B)$.

$\therefore P(A \mid B)=\frac{P(A \cap B)}{P(B)}=\frac{\frac{2}{36}}{\frac{6}{35}}=\frac{2}{6}=\frac{1}{3}$

(b) E: Sum of the observations is 8 .

$={(2,6),(3,5),(4,4),(5,3),(6,2)}$

$F$ : Red die resulted in a number less than 4.

$$=\begin{bmatrix}(1,1),(1,2),(1,3),(2,1),(2,2),(2,3), \\ (3,1),(3,2),(3,3),(4,1),(4,2),(4,3), \\ (5,1),(5,2),(5,3),(6,1),(6,2),(6,3)\end{bmatrix}$$

$\begin{aligned} & \therefore E \cap F=\{(5,3),(6,2)\} \\ & P(F)=\frac{18}{36} \text { and } P(E \cap F)=\frac{2}{36}\end{aligned}$

The conditional probability of obtaining the sum equal to 8 , given that the red die resulted in a number less than 4 , is given by $P$ (E|F).

Therefore, $P(E \mid F)=\frac{P(E \cap F)}{P(F)}=\frac{\frac{2}{36}}{\frac{18}{36}}=\frac{2}{18}=\frac{1}{9}$

11. A fair die is rolled. Consider events $E={1,3,5}, F={2,3}$ and $G={2,3,4,5}$ Find

(i) $P(E \mid F)$ and $P(F \mid E)$

(ii) $P(E \mid G)$ and $P(G \mid E)$

(iii) $P((E \cup F) \mid G)$ and $P((E \cap F) \mid G)$

Solution

When a fair die is rolled, the sample space $S$ will be

$S={1,2,3,4,5,6}$

It is given that $E={1,3,5}, F={2,3}$, and $G={2,3,4,5}$

$\therefore P(E)=\frac{3}{6}=\frac{1}{2}$

$P(F)=\frac{2}{6}=\frac{1}{3}$

$P(G)=\frac{4}{6}=\frac{2}{3}$

(i) $E \cap F={3}$

$\therefore P(E \cap F)=\frac{1}{6}$

$\therefore P(E \mid F)=\frac{P(E \cap F)}{P(F)}=\frac{\frac{1}{6}}{\frac{1}{3}}=\frac{1}{2}$

$P(F \mid E)=\frac{P(E \cap F)}{P(E)}=\frac{\frac{1}{6}}{\frac{1}{2}}=\frac{1}{3}$

(ii) $E \cap G={3,5}$ $\therefore P(E \cap G)=\frac{2}{6}=\frac{1}{3}$

$\therefore P(E \mid G)=\frac{P(E \cap G)}{P(G)}=\frac{\frac{1}{3}}{\frac{2}{3}}=\frac{1}{2}$

$P(G \mid E)=\frac{P(E \cap G)}{P(E)}=\frac{\frac{1}{3}}{\frac{1}{2}}=\frac{2}{3}$

(iii) $E \cup F={1,2,3,5}$

$(E \cup F) \cap G={1,2,3,5} \cap{2,3,4,5}={2,3,5}$

$E \cap F={3}$

$(E \cap F) \cap G={3} \cap{2,3,4,5}={3}$ $\therefore P(E \cup G)=\frac{4}{6}=\frac{2}{3}$

$P((E \cup F) \cap G)=\frac{3}{6}=\frac{1}{2}$

$P(E \cap F)=\frac{1}{6}$

$P((E \cap F) \cap G)=\frac{1}{6}$

$\therefore P((E \cup F) \mid G)=\frac{P((E \cup F) \cap G)}{P(G)}$

$=\frac{\frac{1}{2}}{\frac{2}{3}}=\frac{1}{2} \times \frac{3}{2}=\frac{3}{4}$

$P((E \cap F) \mid G)=\frac{P((E \cap G) \cap G)}{P(G)}$

$=\frac{\frac{1}{6}}{\frac{2}{3}}=\frac{1}{6} \times \frac{3}{2}=\frac{1}{4}$

12. Assume that each born child is equally likely to be a boy or a girl. If a family has two children, what is the conditional probability that both are girls given that (i) the youngest is a girl, (ii) at least one is a girl?

Solution

Let $b$ and $g$ represent the boy and the girl child respectively. If a family has two children, the sample space will be

$S={(b, b),(b, g),(g, b),(g, g)}$

Let $A$ be the event that both children are girls.

$\therefore A={(g, g)}$

(i) Let $B$ be the event that the youngest child is a girl. $\therefore B=[(b, g),(g, g)]$

$\Rightarrow A \cap B={(g, g)}$

$\therefore P(B)=\frac{2}{4}=\frac{1}{2}$

$P(A \cap B)=\frac{1}{4}$

The conditional probability that both are girls, given that the youngest child is a girl, is given by $P(A \mid B)$.

$P(A \mid B)=\frac{P(A \cap B)}{P(B)}=\frac{\frac{1}{4}}{\frac{1}{2}}=\frac{1}{2}$

Therefore, the required probability is $\frac{1}{2}$.

(ii) Let $C$ be the event that at least one child is a girl.

$\therefore C={(b, g),(g, b),(g, g)}$

$\Rightarrow A \cap C={g, g}$

$\Rightarrow P(C)=\frac{3}{4}$

$P(A \cap C)=\frac{1}{4}$

The conditional probability that both are girls, given that at least one child is a girl, is given by $P(A \mid C)$.

Therefore, $P(A \mid C)=\frac{P(A \cap C)}{P(C)}=\frac{\frac{1}{4}}{\frac{3}{4}}=\frac{1}{3}$

13. An instructor has a question bank consisting of 300 easy True / False questions, 200 difficult True / False questions, 500 easy multiple choice questions and 400 difficult multiple choice questions. If a question is selected at random from the question bank, what is the probability that it will be an easy question given that it is a multiple choice question?

Solution

The given data can be tabulated as

	True/False	Multiple choice	Total
Easy	300	500	800
Difficult	200	400	600
Total	500	900	1400

Let us denote $E=$ easy questions, $M=$ multiple choice questions, $D=$ difficult questions, and $T=$ True/False questions

Total number of questions $=1400$

Total number of multiple choice questions $=900$

Therefore, probability of selecting an easy multiple choice question is

$P(E \cap M)=\frac{500}{1400}=\frac{5}{14}$

Probability of selecting a multiple choice question, $P(M)$, is $\frac{900}{1400}=\frac{9}{14}$

$P(E \mid M)$ represents the probability that a randomly selected question will be an easy question, given that it is a multiple choice question.

$\therefore P(E \mid M)=\frac{P(E \cap M)}{P(M)}=\frac{\frac{5}{14}}{\frac{9}{14}}=\frac{5}{9}$

Therefore, the required probability is $\frac{5}{9}$.

14. Given that the two numbers appearing on throwing two dice are different. Find the probability of the event ’the sum of numbers on the dice is 4 ‘.

Solution

When dice is thrown, number of observations in the sample space $=6 \times 6=36$

Let $A$ be the event that the sum of the numbers on the dice is 4 and $B$ be the event that the two numbers appearing on throwing the two dice are different.

$ \begin{aligned} & \therefore A={(1,3),(2,2),(3,1)} \\ & B={\begin{matrix} (1,2),(1,3),(1,4),(1,5),(1,6) \\ (2,1),(2,2),(2,3),(2,4),(2,5),(2,6) \\ (3,1),(3,2),(3,3),(3,4),(3,5),(3,6) \\ (4,1),(4,2),(4,3),(4,4),(4,5),(4,6) \\ (5,1),(5,2),(5,3),(5,4),(5,5),(5,6) \\ (6,1),(6,2),(6,3),(6,4),(6,5),(6,6) \end{matrix} } \end{aligned} $

$A \cap B={(1,3),(3,1)}$

$\therefore P(B)=\frac{30}{36}=\frac{5}{6}$ and $P(A \cap B)=\frac{2}{36}=\frac{1}{18}$

Let $P(A \mid B)$ represent the probability that the sum of the numbers on the dice is 4 , given that the two numbers appearing on throwing the two dice are different.

$ \therefore P(A \mid B)=\frac{P(A \cap B)}{P(B)}=\frac{\frac{1}{18}}{\frac{5}{6}}=\frac{1}{15} $

Therefore, the required probability is $\frac{1}{15}$.

15. Consider the experiment of throwing a die, if a multiple of 3 comes up, throw the die again and if any other number comes, toss a coin. Find the conditional probability of the event ’the coin shows a tail’, given that ‘at least one die shows a 3’.

Solution

The outcomes of the given experiment can be represented by the following tree diagram.

The sample space of the experiment is,

$ S={\begin{matrix} (1, H),(1, T),(2, H),(2, T),(3,1)(3,2),(3,3),(3,4),(3,5),(3,6), \\ (4, H),(4, T),(5, H),(5, T),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6) \end{matrix} } $

Let $A$ be the event that the coin shows a tail and $B$ be the event that at least one die shows 3.

$ \begin{aligned} & \therefore A={(1, T),(2, T),(4, T),(5, T)} \\ & B={(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(6,3)} \\ & \Rightarrow A \cap B=\phi \\ & \therefore P(A \cap B)=0 \end{aligned} $

Then, $P(B)=P({3,1})+P({3,2})+P({3,3})+P({3,4})+P({3,5})+P({3,6})+P({6,3})$

$ \begin{aligned} & =\frac{1}{36}+\frac{1}{36}+\frac{1}{36}+\frac{1}{36}+\frac{1}{36}+\frac{1}{36}+\frac{1}{36} \\ & =\frac{7}{36} \end{aligned} $

Probability of the event that the coin shows a tail, given that at least one die shows 3, is given by $P(A \mid B)$.

Therefore,

$ P(A \mid B)=\frac{P(A \cap B)}{P(B)}=\frac{0}{\frac{7}{36}}=0 $

In each of the Exercises 16 and 17 choose the correct answer:

16. If $P(A)=\frac{1}{2}, P(B)=0$, then $P(A \mid B)$ is (A) 0 (B) $\frac{1}{2}$ (C) not defined (D) 1

Solution

It is given that $P(A)=\frac{1}{2}$ and $P(B)=0$ $P(A \mid B)=\frac{P(A \cap B)}{P(B)}=\frac{P(A \cap B)}{0}$

Therefore, $P(A \mid B)$ is not defined.

Thus, the correct answer is $C$.

17. If $A$ and $B$ are events such that $P(A \mid B)=P(B \mid A)$, then (A) $A \subset B$ but $A \neq B$ (B) $A=B$ (C) $A \cap B=\phi$ (D) $P(A)=P(B)$

Solution

It is given that, $P(A \mid B)=P(B \mid A)$

$\Rightarrow \frac{P(A \cap B)}{P(B)}=\frac{P(A \cap B)}{P(A)}$

$\Rightarrow P(A)=P(B)$

Thus, the correct answer is D.

Multiplication Theorem on Probability

Let $E$ and $F$ be two events associated with a sample space $S$. Clearly, the set $E \cap F$ denotes the event that both $E$ and $F$ have occurred. In other words, $E \cap F$ denotes the simultaneous occurrence of the events $E$ and $F$. The event $E \cap F$ is also written as $EF$.

Very often we need to find the probability of the event EF. For example, in the experiment of drawing two cards one after the other, we may be interested in finding the probability of the event ‘a king and a queen’. The probability of event EF is obtained by using the conditional probability as obtained below :

We know that the conditional probability of event $E$ given that $F$ has occurred is denoted by $P(E \mid F)$ and is given by

$ P(E \mid F)=\frac{P(E \cap F)}{P(F)}, P(F) \neq 0 $

From this result, we can write

$ P(E \cap F)=P(F) . P(E \mid F) $

Also, we know that

or

$ \begin{aligned} & P(F \mid E)=\frac{P(F \cap E)}{P(E)}, P(E) \neq 0 \\ & P(F \mid E)=\frac{P(E \cap F)}{P(E)}(\text{ since } E \cap F=F \cap E) \end{aligned} $

Thus,

$ P(E \cap F)=P(E) . P(F \mid E) $

Combining (1) and (2), we find that

$ \begin{aligned} P(E \cap F) & =P(E) P(F \mid E) \\ & =P(F) P(E \mid F) \text{ provided } P(E) \neq 0 \text{ and } P(F) \neq 0 . \end{aligned} $

The above result is known as the multiplication rule of probability.

Let us now take up an example.

Example 8 An urn contains 10 black and 5 white balls. Two balls are drawn from the urn one after the other without replacement. What is the probability that both drawn balls are black?

Solution Let $E$ and $F$ denote respectively the events that first and second ball drawn are black. We have to find $P(E \cap F)$ or $P(EF)$.

Now

$ P(E)=P(\text{ black ball in first draw })=\frac{10}{15} $

Also given that the first ball drawn is black, i.e., event $E$ has occurred, now there are 9 black balls and five white balls left in the urn. Therefore, the probability that the second ball drawn is black, given that the ball in the first draw is black, is nothing but the conditional probability of $F$ given that $E$ has occurred.

i.e.

$ P(F \mid E)=\frac{9}{14} $

By multiplication rule of probability, we have

$ \begin{aligned} P(E \cap F) & =P(E) P(F \mid E) \\ & =\frac{10}{15} \times \frac{9}{14}=\frac{3}{7} \end{aligned} $

Multiplication rule of probability for more than two events If $E, F$ and $G$ are three events of sample space, we have

$ P(E \cap F \cap G)=P(E) P(F \mid E) P(G \mid(E \cap F))=P(E) P(F \mid E) P(G \mid E F) $

Similarly, the multiplication rule of probability can be extended for four or more events.

The following example illustrates the extension of multiplication rule of probability for three events.

Example 9 Three cards are drawn successively, without replacement from a pack of 52 well shuffled cards. What is the probability that first two cards are kings and the third card drawn is an ace?

Solution Let $K$ denote the event that the card drawn is king and $A$ be the event that the card drawn is an ace. Clearly, we have to find P (KKA)

Now

$ P(K)=\frac{4}{52} $

Also, $P(K \mid K)$ is the probability of second king with the condition that one king has already been drawn. Now there are three kings in $(52-1)=51$ cards.

Therefore

$ P(K \mid K)=\frac{3}{51} $

Lastly, $P(A \mid KK)$ is the probability of third drawn card to be an ace, with the condition that two kings have already been drawn. Now there are four aces in left 50 cards.

Therefore

$ P(A \mid KK)=\frac{4}{50} $

By multiplication law of probability, we have

$ \begin{aligned} P(KKA) & =P(K) \quad P(K \mid K) \quad P(A \mid KK) \\ & =\frac{4}{52} \times \frac{3}{51} \times \frac{4}{50}=\frac{2}{5525} \end{aligned} $

Independent Events

Consider the experiment of drawing a card from a deck of 52 playing cards, in which the elementary events are assumed to be equally likely. If $E$ and $F$ denote the events ’the card drawn is a spade’ and ’the card drawn is an ace’ respectively, then

$ P(E)=\frac{13}{52}=\frac{1}{4} \text{ and } P(F)=\frac{4}{52}=\frac{1}{13} $

Also $E$ and $F$ is the event ’ the card drawn is the ace of spades’ so that

Hence

$ \begin{aligned} & P(E \cap F)=\frac{1}{52} \\ & P(E \mid F)=\frac{P(E \cap F)}{P(F)}=\frac{\frac{1}{52}}{\frac{1}{13}}=\frac{1}{4} \end{aligned} $

Since $P(E)=\frac{1}{4}=P(E \mid F)$, we can say that the occurrence of event $F$ has not affected the probability of occurrence of the event $E$.

We also have

$ P(F \mid E)=\frac{P(E \cap F)}{P(E)}=\frac{\frac{1}{52}}{\frac{1}{4}}=\frac{1}{13}=P(F) $

Again, $P(F)=\frac{1}{13}=P(F \mid E)$ shows that occurrence of event $E$ has not affected the probability of occurrence of the event $F$.

Thus, $E$ and $F$ are two events such that the probability of occurrence of one of them is not affected by occurrence of the other.

Such events are called independent events.

Definition 2 Two events $E$ and $F$ are said to be independent, if

$ \begin{aligned} & P(F \mid E)=P(F) \text{ provided } P(E) \neq 0 \\ & P(E \mid F)=P(E) \text{ provided } P(F) \neq 0 \end{aligned} $

and

Thus, in this definition we need to have $P(E) \neq 0$ and $P(F) \neq 0$

Now, by the multiplication rule of probability, we have

$ P(E \cap F)=P(E) \cdot P(F \mid E) $

If $E$ and $F$ are independent, then (1) becomes

$ P(E \cap F)=P(E) \cdot P(F) $

Thus, using (2), the independence of two events is also defined as follows:

Definition 3 Let $E$ and $F$ be two events associated with the same random experiment, then $E$ and $F$ are said to be independent if

$ P(E \cap F)=P(E) . P(F) $

Remarks

(i) Two events $E$ and $F$ are said to be dependent if they are not independent, i.e. if

$ P(E \cap F) \neq P(E) . P(F) $

(ii) Sometimes there is a confusion between independent events and mutually exclusive events. Term ‘independent’ is defined in terms of ‘probability of events’ whereas mutually exclusive is defined in term of events (subset of sample space). Moreover, mutually exclusive events never have an outcome common, but independent events, may have common outcome. Clearly, ‘independent’ and ‘mutually exclusive’ do not have the same meaning.

In other words, two independent events having nonzero probabilities of occurrence can not be mutually exclusive, and conversely, i.e. two mutually exclusive events having nonzero probabilities of occurrence can not be independent.

(iii) Two experiments are said to be independent if for every pair of events $E$ and $F$, where $E$ is associated with the first experiment and $F$ with the second experiment, the probability of the simultaneous occurrence of the events $E$ and $F$ when the two experiments are performed is the product of $P(E)$ and $P(F)$ calculated separately on the basis of two experiments, i.e., $P(E \cap F)=P(E)$. $P(F)$

(iv) Three events A, B and C are said to be mutually independent, if

$ \begin{aligned} P(A \cap B) & =P(A) P(B) \\ P(A \cap C) & =P(A) P(C) \\ P(B \cap C) & =P(B) P(C) \end{aligned} $

$ \text{ and } \quad P(A \cap B \cap C)=P(A) P(B) P(C) $

If at least one of the above is not true for three given events, we say that the events are not independent.

Example 10 $A$ die is thrown. If $E$ is the event ’the number appearing is a multiple of 3 ’ and $F$ be the event ’the number appearing is even’ then find whether $E$ and $F$ are independent?

Solution We know that the sample space is $S={1,2,3,4,5,6}$

Now

$ E={3,6}, F={2,4,6} \text{ and } E \cap F={6} $

Then

$ P(E)=\frac{2}{6}=\frac{1}{3}, P(F)=\frac{3}{6}=\frac{1}{2} \text{ and } P(E \cap F)=\frac{1}{6} $

Clearly

$ P(E \cap F)=P(E) \cdot P(F) $

Hence $\quad E$ and $F$ are independent events.

Example 11 An unbiased die is thrown twice. Let the event A be ‘odd number on the first throw’ and B the event ‘odd number on the second throw’. Check the independence of the events A and B.

Solution If all the 36 elementary events of the experiment are considered to be equally likely, we have

Also

$ P(A)=\frac{18}{36}=\frac{1}{2} \text{ and } P(B)=\frac{18}{36}=\frac{1}{2} $

$ P(A \cap B)=P(\text{ odd number on both throws }) $

$ =\frac{9}{36}=\frac{1}{4} $

Now

$ P(A) P(B)=\frac{1}{2} \times \frac{1}{2}=\frac{1}{4} $

Clearly

$ P(A \cap B)=P(A) \times P(B) $

Thus, $\quad A$ and $B$ are independent events

Example 12 Three coins are tossed simultaneously. Consider the event $E$ ’three heads or three tails’, $F$ ‘at least two heads’ and $G$ ‘at most two heads’. Of the pairs (E,F), $(E, G)$ and $(F, G)$, which are independent? which are dependent?

Solution The sample space of the experiment is given by

Clearly $\quad E={HHH, TTT}, F={HHH, HHT, HTH, THH}$

$ S={HHH, HHT, HTH, THH, HTT, THT, TTH, TTT} $

$ E={HHH, TTT}, F={HHH, HHT, HTH, THH} $ and

$ G={HHT, HTH, THH, HTT, THT, TTH, TTT} $

Also $E \cap F={HHH}, E \cap G={TTT}, F \cap G={HHT, HTH, THH}$

Therefore

$ P(E)=\frac{2}{8}=\frac{1}{4}, P(F)=\frac{4}{8}=\frac{1}{2}, P(G)=\frac{7}{8} $

and

$ P(E \cap F)=\frac{1}{8}, P(E \cap G)=\frac{1}{8}, P(F \cap G)=\frac{3}{8} $

Also

$ P(E) \cdot P(F)=\frac{1}{4} \times \frac{1}{2}=\frac{1}{8}, P(E) \cdot P(G)=\frac{1}{4} \times \frac{7}{8}=\frac{7}{32} $

and

$ P(F) \cdot P(G)=\frac{1}{2} \times \frac{7}{8}=\frac{7}{16} $

Thus

$ P(E \cap F)=P(E) \cdot P(F) $

$ P(E \cap G) \neq P(E) \cdot P(G) $

and

$ P(F \cap G) \neq P(F) . P(G) $

Hence, the events ( $E$ and $F$ ) are independent, and the events $(E$ and $G)$ and $(F$ and $G)$ are dependent.

Example 13 Prove that if $E$ and $F$ are independent events, then so are the events $E$ and $F^{\prime}$.

Solution Since $E$ and $F$ are independent, we have

$ P(E \cap F)=P(E) . P(F) $

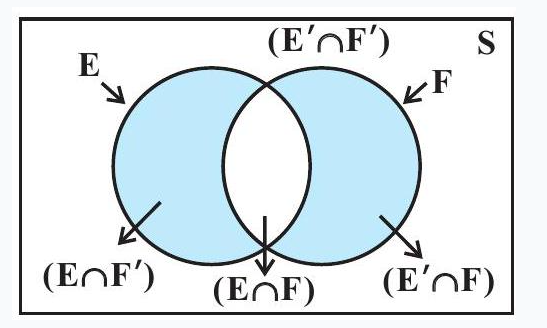
From the venn diagram in Fig 13.3, it is clear that $E \cap F$ and $E \cap F^{\prime}$ are mutually exclusive events and also $E=(E \cap F) \cup(E \cap F^{\prime})$.

Therefore

$ P(E)=P(E \cap F)+P(E \cap F^{\prime}) $

or

$ \begin{aligned} P(E \cap F^{\prime})= & P(E)-P(E \cap F) \\ = & P(E)-P(E) \cdot P(F) \\ & (\text{ by }(1)) \\ = & P(E)(1-P(F)) \\ = & P(E) \cdot P(F^{\prime}) \end{aligned} $

Hence, $E$ and $F^{\prime}$ are independent

Note In a similar manner, it can be shown that if the events $E$ and $F$ are independent, then

(a) $E^{\prime}$ and $F$ are independent,

(b) $E^{\prime}$ and $F^{\prime}$ are independent

Example 14 If $A$ and $B$ are two independent events, then the probability of occurrence of at least one of $A$ and $B$ is given by $1-P(A^{\prime}) P(B^{\prime})$

Solution We have

$ \begin{aligned} & P(\text{ at least one of } A \text{ and } B)=P(A \cup B) \\ &=P(A)+P(B)-P(A \cap B) \\ &=P(A)+P(B)-P(A) P(B) \\ &=P(A)+P(B)[1-P(A)] \\ &=P(A)+P(B) . P(A^{\prime}) \\ &=1-P(A^{\prime})+P(B) P(A^{\prime}) \\ &=1-P(A^{\prime})[1-P(B)] \\ &=1-P(A^{\prime}) P(B^{\prime}) \\ & \text{ EXERCISE } 13.2 \end{aligned} $

EXERCISE 13.2

1. If $P(A)=\frac{3}{5}$ and $P(B)=\frac{1}{5}$, find $P(A \cap B)$ if $A$ and $B$ are independent events.

Solution

It is given that $P(A)=\frac{3}{5}$ and $P(B)=\frac{1}{5}$

$A$ and $B$ are independent events. Therefore,

$ P(A \cap B)=P(A) \cdot P(B)=\frac{3}{5} \cdot \frac{1}{5}=\frac{3}{25} $

2. Two cards are drawn at random and without replacement from a pack of 52 playing cards. Find the probability that both the cards are black.

Solution

There are 26 black cards in a deck of 52 cards.

Let $P(A)$ be the probability of getting a black card in the first draw.

$\therefore P(A)=\frac{26}{52}=\frac{1}{2}$

Let $P(B)$ be the probability of getting a black card on the second draw.

Since the card is not replaced,

$\therefore P(B)=\frac{25}{51}$

Thus, probability of getting both the cards black $=\frac{1}{2} \times \frac{25}{51}=\frac{25}{102}$

3. A box of oranges is inspected by examining three randomly selected oranges drawn without replacement. If all the three oranges are good, the box is approved for sale, otherwise, it is rejected. Find the probability that a box containing 15 oranges out of which 12 are good and 3 are bad ones will be approved for sale.

Solution

Let $A, B$, and $C$ be the respective events that the first, second, and third drawn orange is good.

Therefore, probability that first drawn orange is good, $P(A)=\frac{12}{15}$

The oranges are not replaced.

Therefore, probability of getting second orange good, $P(B)=\frac{11}{14}$

Similarly, probability of getting third orange good, $P(C)=\frac{10}{13}$

The box is approved for sale, if all the three oranges are good.

Thus, probability of getting all the oranges good $=\frac{12}{15} \times \frac{11}{14} \times \frac{10}{13}=\frac{44}{91}$

Therefore, the probability that the box is approved for sale is $\frac{44}{91}$.

4. A fair coin and an unbiased die are tossed. Let A be the event ‘head appears on the coin’ and B be the event ’ 3 on the die’. Check whether A and B are independent events or not.

Solution

If a fair coin and an unbiased die are tossed, then the sample space $S$ is given by,

$S=\begin{cases} (H, 1),(H, 2),(H, 3),(H, 4),(H, 5),(H, 6), \\ (T, 1),(T, 2),(T, 3),(T, 4),(T, 5),(T, 6) \end{cases} $

Let A: Head appears on the coin

$A={(H, 1),(H, 2),(H, 3),(H, 4),(H, 5),(H, 6)}$

$\Rightarrow P(A)=\frac{6}{12}=\frac{1}{2}$

B: 3 on die $={(H, 3),(T, 3)}$

$P(B)=\frac{2}{12}=\frac{1}{6}$ $\therefore A \cap B={(H, 3)}$

$P(A \cap B)=\frac{1}{12}$

$P(A) \cdot P(B)=\frac{1}{2} \times \frac{1}{6}=P(A \cap B)$

Therefore, $A$ and $B$ are independent events.

5. A die marked 1,2,3 in red and 4, 5, 6 in green is tossed. Let A be the event, ’the number is even,’ and B be the event, ’the number is red’. Are A and B independent?

Solution

When a die is thrown, the sample space (S) is

$S={1,2,3,4,5,6}$

Let $A$ : the number is even $={2,4,6}$

$\Rightarrow P(A)=\frac{3}{6}=\frac{1}{2}$

$B:$ the number is red $={1,2,3}$

$\Rightarrow P(B)=\frac{3}{6}=\frac{1}{3}$

$\therefore A \cap B={2}$ $P(A B)=P(A \cap B)=\frac{1}{6}$

$P(A) \cdot P(B)=\frac{1}{2} \times \frac{1}{2}=\frac{1}{4} \neq \frac{1}{6}$

$\Rightarrow P(A) \cdot P(B) \neq P(AB)$

Therefore, A and B are not independent.

6. Let $E$ and $F$ be events with $P(E)=\frac{3}{5}, P(F)=\frac{3}{10}$ and $P(E \cap F)=\frac{1}{5}$. Are $E$ and $F$ independent?

Solution

It is given that $P(E)=\frac{3}{5}, P(F)=\frac{3}{10}$, and $P(EF)=P(E \cap F)=\frac{1}{5}$

$P(E) \cdot P(F)=\frac{3}{5} \cdot \frac{3}{10}=\frac{9}{50} \neq \frac{1}{5}$

$\Rightarrow P(E) \cdot P(F) \neq P(EF)$

Therefore, $E$ and $F$ are not independent.

7. Given that the events $A$ and $B$ are such that $P(A)=\frac{1}{2}, P(A \cup B)=\frac{3}{5}$ and $P(B)=p$. Find $p$ if they are (i) mutually exclusive (ii) independent.

Solution

It is given that $P(A)=\frac{1}{2}, P(A \cap B)=\frac{3}{5}$, and $P(B)=p$

(i) When $A$ and $B$ are mutually exclusive, $A \cap B=\Phi$

$\therefore P(A \cap B)=0$

It is known that, $P(A \cup B)=P(A)+P(B)-P(A \cap B)$

$ \begin{aligned} & \Rightarrow \frac{3}{5}=\frac{1}{2}+p-0 \\ & \Rightarrow p=\frac{3}{5}-\frac{1}{2}=\frac{1}{10} \end{aligned} $

(ii) When $A$ and $B$ are independent, $P(A \cap B)=P(A) \cdot P(B)=\frac{1}{2} p$

It is known that, $P(A \cup B)=P(A)+P(B)-P(A \cap B)$

$\Rightarrow \frac{3}{5}=\frac{1}{2}+p-\frac{1}{2} p$

$\Rightarrow \frac{3}{5}=\frac{1}{2}+\frac{p}{2}$

$\Rightarrow \frac{p}{2}=\frac{3}{5}-\frac{1}{2}=\frac{1}{10}$

$\Rightarrow p=\frac{2}{10}=\frac{1}{5}$

8. Let $A$ and $B$ be independent events with $P(A)=0.3$ and $P(B)=0.4$. Find (i) $P(A \cap B)$ (ii) $P(A \cup B)$ (iii) $P(A \mid B)$ (iv) $P(B \mid A)$

Solution

It is given that $P(A)=0.3$ and $P(B)=0.4$

(i) If $A$ and $B$ are independent events, then

$P(A \cap B)=P(A) \cdot P(B)=0.3 \times 0.4=0.12$

(ii) It is known that, $P(A \cup B)=P(A)+P(B)-P(A \cap B)$

$\Rightarrow P(A \cup B)=0.3+0.4-0.12=0.58$ (iii) It is known that, $P(A \mid B)=\frac{P(A \cap B)}{P(B)}$

$\Rightarrow P(A \mid B)=\frac{0.12}{0.4}=0.3$

(iv) It is known that, $P(B \mid A)=\frac{P(A \cap B)}{P(A)}$

$\Rightarrow P(B \mid A)=\frac{0.12}{0.3}=0.4$

9. If $A$ and $B$ are two events such that $P(A)=\frac{1}{4}, P(B)=\frac{1}{2}$ and $P(A \cap B)=\frac{1}{8}$, find $P($ not $A$ and not $B)$.

Solution

It is given that, $P(A)=\frac{1}{2}$ and $P(A \cap B)=\frac{1}{8}$

$P(not$ on $A$ and not on $B)=P(A^{\prime} \cap B^{\prime})$

$P(not$ on $A$ and not on $B)=P((A \cup B))^{\prime}$

$=1-P(A \cup B)$

$ [A^{\prime} \cap B^{\prime}=(A \cup B)^{\prime}] $

$=1-[P(A)+P(B)-P(A \cap B)]$

$=1-[\frac{1}{4}+\frac{1}{2}-\frac{1}{8}]$

$=1-\frac{5}{8}$

$=\frac{3}{8}$

10. Events $A$ and $B$ are such that $P(A)=\frac{1}{2}, P(B)=\frac{7}{12}$ and $P(not A$ or not $B)=\frac{1}{4}$. State whether A and B are independent?

Solution

It is given that $P(A)=\frac{1}{2}, P(B)=\frac{7}{12}$, and $P(not A$ or $not B)=\frac{1}{4}$

$\Rightarrow P(A^{\prime} \cup B^{\prime})=\frac{1}{4}$

$\Rightarrow P((A \cap B)^{\prime})=\frac{1}{4} \quad[A^{\prime} \cup B^{\prime}=(A \cap B)^{\prime}]$

$\Rightarrow 1-P(A \cap B)=\frac{1}{4}$

$\Rightarrow P(A \cap B)=\frac{3}{4}$

However, $P(A) \cdot P(B)=\frac{1}{2} \cdot \frac{7}{12}=\frac{7}{24}$

Here, $\frac{3}{4} \neq \frac{7}{24}$

$\therefore P(A \cap B) \neq P(A) \cdot P(B)$

Therefore, A and B are independent events.

11. Given two independent events $A$ and $B$ such that $P(A)=0.3, P(B)=0.6$. Find (i) $P(A$ and $B)$ (ii) $P(A$ and not $B)$ (iii) $P(A$ or $B)$ (iv) $P$ (neither $A$ nor $B$ )

Solution

It is given that $P(A)=0.3$ and $P(B)=0.6$

Also, $A$ and $B$ are independent events.

(i) $\therefore P(A$ and $B)=P(A) \cdot P(B)$

$\Rightarrow P(A \cap B)=0.3 \times 0.6=0.18$

(ii) $P(A$ and not $B)=P(A \cap B^{\prime})$ $=P(A)-P(A \cap B)$

$=0.3-0.18$

$=0.12$

(iii) $P(A$ or $B)=P(A \cup B)$

$=P(A)+P(B)-P(A \cap B)$

$=0.3+0.6-0.18$

$=0.72$

(iv) $P($ neither $A$ nor $B)=P(A^{\prime} \cap B^{\prime})$

$=P((A \cup B)^{\prime})$

$=1-P(A \cup B)$

$=1-0.72$

$=0.28$

12. A die is tossed thrice. Find the probability of getting an odd number at least once.

Solution

Probability of getting an odd number in a single throw of a die $=\frac{3}{6}=\frac{1}{2}$

Similarly, probability of getting an even number $=\frac{3}{6}=\frac{1}{2}$

Probability of getting an even number three times $=\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}=\frac{1}{8}$

Therefore, probability of getting an odd number at least once

$=1-$ Probability of getting an odd number in none of the throws

$=1-$ Probability of getting an even number thrice

$=1-\frac{1}{8}$

$=\frac{7}{8}$

13. Two balls are drawn at random with replacement from a box containing 10 black and 8 red balls. Find the probability that

(i) both balls are red.

(ii) first ball is black and second is red.

(iii) one of them is black and other is red.

Solution

Total number of balls $=18$

Number of red balls $=8$

Number of black balls $=10$

(i) Probability of getting a red ball in the first draw $=\frac{8}{18}=\frac{4}{9}$

The ball is replaced after the first draw.

$\therefore$ Probability of getting a red ball in the second draw $=\frac{8}{18}=\frac{4}{9}$

Therefore, probability of getting both the balls red $=\frac{4}{9} \times \frac{4}{9}=\frac{16}{81}$

(ii) Probability of getting first ball black $=\frac{10}{18}=\frac{5}{9}$

The ball is replaced after the first draw.

Probability of getting second ball as red $=\frac{8}{18}=\frac{4}{9}$

Therefore, probability of getting first ball as black and second ball as red $=\frac{5}{9} \times \frac{4}{9}=\frac{20}{81}$

(iii) Probability of getting first ball as red $=\frac{8}{18}=\frac{4}{9}$

The ball is replaced after the first draw.

Probability of getting second ball as black $=\frac{10}{18}=\frac{5}{9}$

Therefore, probability of getting first ball as black and second ball as red $=\frac{4}{9} \times \frac{5}{9}=\frac{20}{81}$ Therefore, probability that one of them is black and other is red

$=$ Probability of getting first ball black and second as red + Probability of getting first ball

red and second ball black $=\frac{20}{81}+\frac{20}{81}$

$ =\frac{40}{81} $

14. Probability of solving specific problem independently by A and B are $\frac{1}{2}$ and $\frac{1}{3}$ respectively. If both try to solve the problem independently, find the probability that

$\begin{matrix} \text{ (i) the problem is solved } & \text{ (ii) exactly one of them solves the problem. }\end{matrix} $

Solution

Probability of solving the problem by $A, P(A)=\frac{1}{2}$

Probability of solving the problem by $B, P(B)=\frac{1}{3}$

Since the problem is solved independently by $A$ and $B$,

$\therefore P(AB)=P(A) \cdot P(B)=\frac{1}{2} \times \frac{1}{3}=\frac{1}{6}$

$P(A^{\prime})=1-P(A)=1-\frac{1}{2}=\frac{1}{2}$

$P(B^{\prime})=1-P(B)=1-\frac{1}{3}=\frac{2}{3}$ i. $\quad$ Probability that the problem is solved $=P(A \cup B)$

$=P(A)+P(B)-P(A B)$ $=\frac{1}{2}+\frac{1}{3}-\frac{1}{6}$

$=\frac{4}{6}$

$=\frac{2}{3}$

(ii) Probability that exactly one of them solves the problem is given by,

$ \begin{aligned} & P(A) \cdot P(B^{\prime})+P(B) \cdot P(A^{\prime}) \\ & =\frac{1}{2} \times \frac{2}{3}+\frac{1}{2} \times \frac{1}{3} \\ & =\frac{1}{3}+\frac{1}{6} \\ & =\frac{1}{2} \end{aligned} $

15. One card is drawn at random from a well shuffled deck of 52 cards. In which of the following cases are the events $E$ and $F$ independent?

(i) $E$ : ’the card drawn is a spade’

$F$ : ’the card drawn is an ace’

(ii) $E$ : ’the card drawn is black’

F : ’the card drawn is a king’

(iii) $E$ : ’the card drawn is a king or queen’

$F$ : ’the card drawn is a queen or jack’.

Solution

(i) In a deck of 52 cards, 13 cards are spades and 4 cards are aces.

$\therefore P(E)=P($ the card drawn is a spade $)=\frac{13}{52}=\frac{1}{4}$ $\therefore P(F)=P($ the card drawn is an ace $)=\frac{4}{52}=\frac{1}{13}$

In the deck of cards, only 1 card is an ace of spades.

$P(E F)=P($ the card drawn is spade and an ace $)=\frac{1}{52}$

$P(E) \times P(F)=\frac{1}{4} \cdot \frac{1}{13}=\frac{1}{52}=P(E F)$

$\Rightarrow P(E) \times P(F)=P(E F)$

Therefore, the events $E$ and $F$ are independent.

(ii) In a deck of 52 cards, 26 cards are black and 4 cards are kings.

$\therefore P(E)=P($ the card drawn is black $)=\frac{26}{52}=\frac{1}{2}$

$\therefore P(F)=P($ the card drawn is a king $)=\frac{4}{52}=\frac{1}{13}$

In the pack of 52 cards, 2 cards are black as well as kings.

$\therefore P(EF)=P($ the card drawn is a black king $)=\frac{2}{52}=\frac{1}{26}$ $P(E) \times P(F)=\frac{1}{2} \cdot \frac{1}{13}=\frac{1}{26}=P(EF)$

Therefore, the given events $E$ and $F$ are independent.

(iii) In a deck of 52 cards, 4 cards are kings, 4 cards are queens, and 4 cards are jacks.

$\therefore P(E)=P($ the card drawn is a king or a queen $)=\frac{8}{52}=\frac{2}{13}$

$\therefore P(F)=P($ the card drawn is a queen or a jack $)=\frac{8}{52}=\frac{2}{13}$

There are 4 cards which are king or queen and queen or jack.

$\therefore P(EF)=P$ (the card drawn is a king or a queen, or queen or a jack)

$=\frac{4}{52}=\frac{1}{13}$

$P(E) \times P(F)=\frac{2}{13} \cdot \frac{2}{13}=\frac{4}{169} \neq \frac{1}{13}$

$\Rightarrow P(E) \cdot P(F) \neq P(EF)$

Therefore, the given events $E$ and $F$ are not independent.

16. In a hostel, $60 %$ of the students read Hindi newspaper, $40 %$ read English newspaper and $20 %$ read both Hindi and English newspapers. A student is selected at random.

(a) Find the probability that she reads neither Hindi nor English newspapers.

(b) If she reads Hindi newspaper, find the probability that she reads English newspaper.

(c) If she reads English newspaper, find the probability that she reads Hindi newspaper.

Solution

Let $H$ denote the students who read Hindi newspaper and $E$ denote the students who read English newspaper.

It is given that,

$ \begin{aligned} & P(H)=60 %=\frac{6}{10}=\frac{3}{5} \\ & P(E)=40 %=\frac{40}{100}=\frac{2}{5} \\ & P(H \cap E)=20 %=\frac{20}{100}=\frac{1}{5} \end{aligned} $

i. Probability that a student reads Hindi or English newspaper is,

$ \begin{aligned} (H \cup E)^{\prime} & =1-P(H \cup E) \\ & =1-{P(H)+P(E)-P(H \cap E)} \\ & =1-(\frac{3}{5}+\frac{2}{5}-\frac{1}{5}) \\ & =1-\frac{4}{5} \\ & =\frac{1}{5} \end{aligned} $

(ii) Probability that a randomly chosen student reads English newspaper, if she reads Hindi news paper, is given by $P(E \mid H)$.

$ \begin{aligned} P(E \mid H) & =\frac{P(E \cap H)}{P(H)} \\ & =\frac{\frac{1}{3}}{\frac{3}{5}} \\ & =\frac{1}{3} \end{aligned} $

(iii) Probability that a randomly chosen student reads Hindi newspaper, if she reads English newspaper, is given by $P(H \mid E)$.

$ \begin{aligned} P(H \mid E) & =\frac{P(H \cap E)}{P(E)} \\ & =\frac{\frac{1}{5}}{\frac{2}{5}} \\ & =\frac{1}{2} \end{aligned} $

Choose the correct answer in Exercises 17 and 18.

17. The probability of obtaining an even prime number on each die, when a pair of dice is rolled is (A) 0 (B) $\frac{1}{3}$ (C) $\frac{1}{12}$ (D) $\frac{1}{36}$

Solution

When two dice are rolled, the number of outcomes is 36 .

The only even prime number is 2 .

Let $E$ be the event of getting an even prime number on each die.

$\therefore E={(2,2)}$

$\Rightarrow P(E)=\frac{1}{36}$

Therefore, the correct answer is D.

18. Two events $A$ and $B$ will be independent, if

(A) $A$ and $B$ are mutually exclusive

(B) $P(A^{\prime} B^{\prime})=[1-P(A)][1-P(B)]$

(C) $P(A)=P(B)$

(D) $P(A)+P(B)=1$

Solution

Two events $A$ and $B$ are said to be independent, if $P(A B)=P(A) \times P(B)$

Consider the result given in alternative $\mathbf{B}$.

$P(A^{\prime} B^{\prime})=[1-P(A)][1-P(B)]$

$\Rightarrow P(A^{\prime} \cap B^{\prime})=1-P(A)-P(B)+P(A) \cdot P(B)$

$\Rightarrow 1-P(A \cup B)=1-P(A)-P(B)+P(A) \cdot P(B)$

$\Rightarrow P(A \cup B)=P(A)+P(B)-P(A) \cdot P(B)$

$\Rightarrow P(A)+P(B)-P(AB)=P(A)+P(B)-P(A) \cdot P(B)$

$\Rightarrow P(AB)=P(A) \cdot P(B)$

This implies that $A$ and $B$ are independent, if $P(A^{\prime} B^{\prime})=[1-P(A)][1-P(B)]$

Distracter Rationale

A. Let $P(A)=m, P(B)=n, 0<m, n<1$

$A$ and $B$ are mutually exclusive.

$\therefore A \cap B=\phi$

$\Rightarrow P(AB)=0$

However, $P(A) \cdot P(B)=m n \neq 0$

$\therefore P(A) \cdot P(B) \neq P(AB)$

C. Let A: Event of getting an odd number on throw of a die $={1,3,5}$

$\Rightarrow P(A)=\frac{3}{6}=\frac{1}{2}$

B: Event of getting an even number on throw of a die $={2,4,6}$

$P(B)=\frac{3}{6}=\frac{1}{2}$

Here, $A \cap B=\phi$

$\therefore P(AB)=0$

$P(A) \cdot P(B)=\frac{1}{4} \neq 0$

$\Rightarrow P(A) \cdot P(B) \neq P(AB)$

D. From the above example, it can be seen that, $P(A)+P(B)=\frac{1}{2}+\frac{1}{2}=1$

However, it cannot be inferred that $A$ and $B$ are independent.

Thus, the correct answer is $B$.

Bayes’ Theorem

Consider that there are two bags I and II. Bag I contains 2 white and 3 red balls and Bag II contains 4 white and 5 red balls. One ball is drawn at random from one of the bags. We can find the probability of selecting any of the bags (i.e. $\frac{1}{2}$ ) or probability of drawing a ball of a particular colour (say white) from a particular bag (say Bag I). In other words, we can find the probability that the ball drawn is of a particular colour, if we are given the bag from which the ball is drawn. But, can we find the probability that the ball drawn is from a particular bag (say Bag II), if the colour of the ball drawn is given? Here, we have to find the reverse probability of Bag II to be selected when an event occurred after it is known. Famous mathematician, John Bayes’ solved the problem of finding reverse probability by using conditional probability. The formula developed by him is known as ‘Bayes theorem’ which was published posthumously in 1763. Before stating and proving the Bayes’ theorem, let us first take up a definition and some preliminary results.

Partition of a sample space

A set of events $E_1, E_2, \ldots, E_n$ is said to represent a partition of the sample space $S$ if

(a) $E_i \cap E_j=\phi, i \neq j, i, j=1,2,3, \ldots, n$ (b) $E_1 \cup E_2 \cup \ldots \cup E_n=S$ and

(c) $P(E_i)>0$ for all $i=1,2, \ldots, n$.

In other words, the events $E_1, E_2, \ldots, E_n$ represent a partition of the sample space $S$ if they are pairwise disjoint, exhaustive and have nonzero probabilities.

As an example, we see that any nonempty event $E$ and its complement $E^{\prime}$ form a partition of the sample space $S$ since they satisfy $E \cap E^{\prime}=\phi$ and $E \cup E^{\prime}=S$.

From the Venn diagram in Fig 13.3, one can easily observe that if $E$ and $F$ are any two events associated with a sample space $S$, then the set ${E \cap F^{\prime}, E \cap F, E^{\prime} \cap F, E^{\prime} \cap F^{\prime}}$ is a partition of the sample space $S$. It may be mentioned that the partition of a sample space is not unique. There can be several partitions of the same sample space.

We shall now prove a theorem known as Theorem of total probability.

Theorem of total probability

Let ${E_1, E_2, \ldots, E_n}$ be a partition of the sample space $S$, and suppose that each of the events $E_1, E_2, \ldots, E_n$ has nonzero probability of occurrence. Let $A$ be any event associated with $S$, then

$ \begin{aligned} P(A) & =P(E_1) P(AlE_1)+P(E_2) P(AlE_2)+\ldots+P(E_n) P(AlE_n) \\ & =\sum _{j=1}^{n} P(E_j) P(AlE_j) \end{aligned} $

Proof Given that $E_1, E_2, \ldots, E_n$ is a partition of the sample space $S$ (Fig 13.4). Therefore,

$ S=E_1 \cup E_2 \cup \ldots \cup E_n $

and

$ E_i \cap E_j=\phi, i \neq j, i, j=1,2, \ldots, n $

Now, we know that for any event $A$,

$ \begin{aligned} A & =A \cap S \\ & =A \cap(E_1 \cup E_2 \cup \ldots \cup E_n) \\ & =(A \cap E_1) \cup(A \cap E_2) \cup \ldots \cup(A \cap E_n) \end{aligned} $

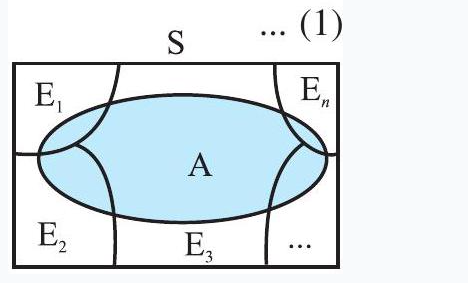
Fig 13.4

Also $A \cap E_i$ and $A \cap E_j$ are respectively the subsets of $E_i$ and $E_j$. We know that $E_i$ and $E_j$ are disjoint, for $i \neq j$, therefore, $A \cap E_i$ and $A \cap E_j$ are also disjoint for all $i \neq j, i, j=1,2, \ldots, n$.

Thus,

$ \begin{aligned} P(A) & =P[(A \cap E_1) \cup(A \cap E_2) \cup \ldots . . \cup(A \cap E_n)] \\ & =P(A \cap E_1)+P(A \cap E_2)+\ldots+P(A \cap E_n) \end{aligned} $

Now, by multiplication rule of probability, we have

$ P(A \cap E_i)=P(E_i) P(AlE_i) \text{ as } P(E_i) \neq 0 \forall i=1,2, \ldots, n $

Therefore,

$ P(A)=P(E_1) P(AlE_1)+P(E_2) P(AlE_2)+\ldots+P(E_n) P(AlE_n) $

or

$ P(A)=\sum _{j=1}^{n} P(E_j) P(AlE_j) $

Example 15 A person has undertaken a construction job. The probabilities are 0.65 that there will be strike, 0.80 that the construction job will be completed on time if there is no strike, and 0.32 that the construction job will be completed on time if there is a strike. Determine the probability that the construction job will be completed on time.

Solution Let A be the event that the construction job will be completed on time, and B be the event that there will be a strike. We have to find $P(A)$.

We have

$ \begin{aligned} P(B) & =0.65, P(\text{ no strike })=P(B^{\prime})=1-P(B)=1-0.65=0.35 \\ P(A \mid B) & =0.32, P(A \mid B^{\prime})=0.80 \end{aligned} $

Since events B and B’ form a partition of the sample space S, therefore, by theorem on total probability, we have

$ \begin{aligned} P(A) & =P(B) P(A \mid B)+P(B^{\prime}) P(A \mid B^{\prime}) \\ & =0.65 \times 0.32+0.35 \times 0.8 \\ & =0.208+0.28=0.488 \end{aligned} $

Thus, the probability that the construction job will be completed in time is 0.488 .

We shall now state and prove the Bayes’ theorem.

Bayes’ Theorem If $E_1, E_2, \ldots, E_n$ are $n$ non empty events which constitute a partition

of sample space $S$, i.e. $E_1, E_2, \ldots, E_n$ are pairwise disjoint and $E_1 \cup E_2 \cup \ldots \cup E_n=S$ and A is any event of nonzero probability, then

$ P(E_i \mid A)=\frac{P(E_i) P(AlE_i)}{\sum _{j=1}^{n} P(E_j) P(AlE_j)} \text{ for any } i=1,2,3, \ldots, n $

Proof By formula of conditional probability, we know that

$ \begin{aligned} P(E_i \mid A) & =\frac{P(A \cap E_i)}{P(A)} \\ & =\frac{P(E_i) P(AlE_i)}{P(A)} \text{ (by multiplication rule of probability) } \\ & =\frac{P(E_i) P(AlE_i)}{\sum _{j=1}^{n} P(E_j) P(AlE_j)} \text{ (by the result of theorem of total probability) } \end{aligned} $

Remark The following terminology is generally used when Bayes’ theorem is applied.

The events $E_1, E_2, \ldots, E_n$ are called hypotheses.

The probability $P(E_i)$ is called the priori probability of the hypothesis $E_i$

The conditional probability $P(E_i \mid A)$ is called a posteriori probability of the hypothesis $E_i$.

Bayes’ theorem is also called the formula for the probability of “causes”. Since the $E_i$ ’s are a partition of the sample space $S$, one and only one of the events $E_i$ occurs (i.e. one of the events $E_i$ must occur and only one can occur). Hence, the above formula gives us the probability of a particular $E_i$ (i.e. a “Cause”), given that the event $A$ has occurred.

The Bayes’ theorem has its applications in variety of situations, few of which are illustrated in following examples.

Example 16 Bag I contains 3 red and 4 black balls while another Bag II contains 5 red and 6 black balls. One ball is drawn at random from one of the bags and it is found to be red. Find the probability that it was drawn from Bag II.

Solution Let $E_1$ be the event of choosing the bag I, $E_2$ the event of choosing the bag II and $A$ be the event of drawing a red ball.

Then

$ P(E_1)=P(E_2)=\frac{1}{2} $

Also

$ P(AlE_1)=P(\text{ drawing a red ball from Bag } I)=\frac{3}{7} $

and

$ P(AlE_2)=P(\text{ drawing a red ball from Bag II })=\frac{5}{11} $

Now, the probability of drawing a ball from Bag II, being given that it is red, is $P(E_2 \mid A)$

By using Bayes’ theorem, we have

$ P(E_2 \mid A)=\frac{P(E_2) P(A_2 E_2)}{P(E_1) P(A_1 E_1)+P(E_2) P(A_I E_2)}=\frac{\frac{1}{2} \times \frac{5}{11}}{\frac{1}{2} \times \frac{3}{7}+\frac{1}{2} \times \frac{5}{11}}=\frac{35}{68} $

Example 17 Given three identical boxes I, II and III, each containing two coins. In box I, both coins are gold coins, in box II, both are silver coins and in the box III, there is one gold and one silver coin. A person chooses a box at random and takes out a coin. If the coin is of gold, what is the probability that the other coin in the box is also of gold?

Solution Let $E_1, E_2$ and $E_3$ be the events that boxes I, II and III are chosen, respectively.

Then

$ P(E_1)=P(E_2)=P(E_3)=\frac{1}{3} $

Also, let A be the event that ’the coin drawn is of gold’

Then

$ \begin{aligned} & P(AIE_1)=P(\text{ a gold coin from bag } I)=\frac{2}{2}=1 \\ & P(AIE_2)=P(\text{ a gold coin from bag II })=0 \\ & P(AIE_3)=P(\text{ a gold coin from bag III })=\frac{1}{2} \end{aligned} $

Now, the probability that the other coin in the box is of gold

$ \begin{aligned} & =\text{ the probability that gold coin is drawn from the box } I \text{. } \\ & =P(E_1 \mid A) \end{aligned} $

By Bayes’ theorem, we know that

$ \begin{aligned} P(E_1 \mid A) & =\frac{P(E_1) P(AlE_1)}{P(E_1) P(AlE E_1)+P(E_2) P(AlE_2)+P(E_3) P(AlE_3)} \\ & =\frac{\frac{1}{3} \times 1}{\frac{1}{3} \times 1+\frac{1}{3} \times 0+\frac{1}{3} \times \frac{1}{2}}=\frac{2}{3} \end{aligned} $

Example 18 Suppose that the reliability of a HIV test is specified as follows:

Of people having HIV, $90 %$ of the test detect the disease but $10 %$ go undetected. Of people free of HIV, $99 %$ of the test are judged HIV-ive but $1 %$ are diagnosed as showing HIV+ive. From a large population of which only $0.1 %$ have HIV, one person is selected at random, given the HIV test, and the pathologist reports him/her as HIV+ive. What is the probability that the person actually has HIV?

Solution Let $E$ denote the event that the person selected is actually having HIV and A the event that the person’s HIV test is diagnosed as +ive. We need to find P(EIA).

Also $E^{\prime}$ denotes the event that the person selected is actually not having HIV.

Clearly, ${E, E^{\prime}}$ is a partition of the sample space of all people in the population. We are given that

$ P(E)=0.1 %=\frac{0.1}{100}=0.001 $

$ \begin{aligned} P(E^{\prime})= & 1-P(E)=0.999 \\ P(A \mid E)= & P(Person \text{ tested as HIV+ive given that he/she } \\ & \quad \text{ is actually having HIV }) \\ = & 90 %=\frac{90}{100}=0.9 \end{aligned} $

and

$P(A \mid E^{\prime})=P($ Person tested as HIV +ive given that he/she is actually not having HIV)

$ =1 %=\frac{1}{100}=0.01 $

Now, by Bayes’ theorem

$ \begin{aligned} P(E \mid A) & =\frac{P(E) P(A \mid E)}{P(E) P(A \mid E)+P(E^{\prime}) P(AlE^{\prime})} \\ & =\frac{0.001 \times 0.9}{0.001 \times 0.9+0.999 \times 0.01}=\frac{90}{1089} \\ & =0.083 \text{ approx. } \end{aligned} $

Thus, the probability that a person selected at random is actually having HIV given that he/she is tested HIV+ive is 0.083 .

Example 19 In a factory which manufactures bolts, machines A, B and C manufacture respectively $25 %, 35 %$ and $40 %$ of the bolts. Of their outputs, 5, 4 and 2 percent are respectively defective bolts. A bolt is drawn at random from the product and is found to be defective. What is the probability that it is manufactured by the machine $B$ ?

Solution Let events $B_1, B_2, B_3$ be the following :

$B_1$ : the bolt is manufactured by machine $A$

$B_2$ : the bolt is manufactured by machine $B$

$B_3$ : the bolt is manufactured by machine $C$

Clearly, $B_1, B_2, B_3$ are mutually exclusive and exhaustive events and hence, they represent a partition of the sample space.

Let the event $E$ be ’the bolt is defective’.

The event $E$ occurs with $B_1$ or with $B_2$ or with $B_3$. Given that,

$ P(B_1)=25 %=0.25, P(B_2)=0.35 \text{ and } P(B_3)=0.40 $

Again $P(E_1 B_1)=$ Probability that the bolt drawn is defective given that it is manufactured by machine $A=5 %=0.05$

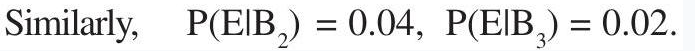
Hence, by Bayes’ Theorem, we have

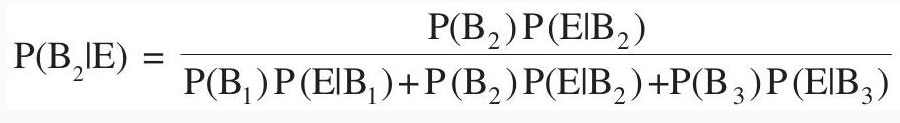
$ \begin{aligned} & =\frac{0.35 \times 0.04}{0.25 \times 0.05+0.35 \times 0.04+0.40 \times 0.02} \\ & =\frac{0.0140}{0.0345}=\frac{28}{69} \end{aligned} $

Example 20 A doctor is to visit a patient. From the past experience, it is known that the probabilities that he will come by train, bus, scooter or by other means of transport

are respectively $\frac{3}{10}, \frac{1}{5}, \frac{1}{10}$ and $\frac{2}{5}$. The probabilities that he will be late are $\frac{1}{4}, \frac{1}{3}$, and $\frac{1}{12}$, if he comes by train, bus and scooter respectively, but if he comes by other means of transport, then he will not be late. When he arrives, he is late. What is the probability that he comes by train?

Solution Let $E$ be the event that the doctor visits the patient late and let $T_1, T_2, T_3, T_4$ be the events that the doctor comes by train, bus, scooter, and other means of transport respectively.

Then

$ P(T_1)=\frac{3}{10}, P(T_2)=\frac{1}{5}, P(T_3)=\frac{1}{10} \text{ and } P(T_4)=\frac{2}{5} \quad \text{ (given) } $

$ P(ElT_1)=\text{ Probability that the doctor arriving late comes by train }=\frac{1}{4} $

Similarly, $P(E \mid T_2)=\frac{1}{3}, P(E \mid T_3)=\frac{1}{12}$ and $P(E \mid T_4)=0$, since he is not late if he comes by other means of transport.

Therefore, by Bayes’ Theorem, we have

$P(T_1 \mid E)=$ Probability that the doctor arriving late comes by train

$ \begin{aligned} & =\frac{P(T_1) P(ElT_1)}{P(T_1) P(E \mid T_1)+P(T_2) P(ElT T_2)+P(T_3) P(ElT_3)+P(T_4) P(ElT_4)} \\ & =\frac{\frac{3}{10} \times \frac{1}{4}}{\frac{3}{10} \times \frac{1}{4}+\frac{1}{5} \times \frac{1}{3}+\frac{1}{10} \times \frac{1}{12}+\frac{2}{5} \times 0}=\frac{3}{40} \times \frac{120}{18}=\frac{1}{2} \end{aligned} $

Hence, the required probability is $\frac{1}{2}$.

Example 21 A man is known to speak truth 3 out of 4 times. He throws a die and reports that it is a six. Find the probability that it is actually a six.

Solution Let $E$ be the event that the man reports that six occurs in the throwing of the die and let $S_1$ be the event that six occurs and $S_2$ be the event that six does not occur.

Then

$ \begin{aligned} & P(S_1)=\text{ Probability that six occurs }=\frac{1}{6} \\ & P(S_2)=\text{ Probability that six does not occur }=\frac{5}{6} \\ & P(ElS_1)=\text{ Probability that the man reports that six occurs when six has } \end{aligned} $

$ \begin{aligned} & =\frac{P(S_1) P(E \mid S_1)}{P(S_1) P(EIS_1)+P(S_2) P(E \mid S_2)} \\ & =\frac{\frac{1}{6} \times \frac{3}{4}}{\frac{1}{6} \times \frac{3}{4}+\frac{5}{6} \times \frac{1}{4}}=\frac{1}{8} \times \frac{24}{8}=\frac{3}{8} \end{aligned} $

Hence, the required probability is $\frac{3}{8}$.

Remark A random variable is a real valued function whose domain is the sample space of a random experiment.

For example, let us consider the experiment of tossing a coin two times in succession.

The sample space of the experiment is $S={HH, HT, TH, TT}$.

If $X$ denotes the number of heads obtained, then $X$ is a random variable and for each outcome, its value is as given below :

$ X(HH)=2, X(HT)=1, X(TH)=1, X(TT)=0 . $

More than one random variables can be defined on the same sample space. For example, let $Y$ denote the number of heads minus the number of tails for each outcome of the above sample space $S$.

Then

$ Y(HH)=2, Y(HT)=0, Y(TH)=0, Y(TT)=-2 $

Thus, $X$ and $Y$ are two different random variables defined on the same sample space $S$.

EXERCISE 13.3

1. An urn contains 5 red and 5 black balls. A ball is drawn at random, its colour is noted and is returned to the urn. Moreover, 2 additional balls of the colour drawn are put in the urn and then a ball is drawn at random. What is the probability that the second ball is red?

Solution

The urn contains 5 red and 5 black balls.

Let a red ball be drawn in the first attempt.

$\therefore P($ drawing a red ball $)=\frac{5}{10}=\frac{1}{2}$

If two red balls are added to the urn, then the urn contains 7 red and 5 black balls.

$P(.$ drawing a red ball) $=\frac{7}{12}$

Let a black ball be drawn in the first attempt.

$\therefore P$ (drawing a black ball in the first attempt) $=\frac{5}{10}=\frac{1}{2}$

If two black balls are added to the urn, then the urn contains 5 red and 7 black balls.

$P($ drawing a red ball $)=\frac{5}{12}$

Therefore, probability of drawing second ball as red is

$\frac{1}{2} \times \frac{7}{12}+\frac{1}{2} \times \frac{5}{12}=\frac{1}{2}(\frac{7}{12}+\frac{5}{12})=\frac{1}{2} \times 1=\frac{1}{2}$

2. A bag contains 4 red and 4 black balls, another bag contains 2 red and 6 black balls. One of the two bags is selected at random and a ball is drawn from the bag which is found to be red. Find the probability that the ball is drawn from the first bag.

Solution

Let $E_1$ and $E_2$ be the events of selecting first bag and second bag respectively. $\therefore P(E_1)=P(E_2)=\frac{1}{2}$

Let $A$ be the event of getting a red ball.

$\Rightarrow P(A \mid E_1)=P($ drawing a red ball from first bag $)=\frac{4}{8}=\frac{1}{2}$

$\Rightarrow P(A \mid E_2)=P($ drawing a red ball from second bag $)=\frac{2}{8}=\frac{1}{4}$

The probability of drawing a ball from the first bag, given that it is red, is given by $P$ $(E_2 \mid A)$.

By using Bayes’ theorem, we obtain

$ \begin{aligned} P(E_1 \mid A) & =\frac{P(E_1) \cdot P(A \mid E_1)}{P(E_1) \cdot P(A \mid E_1)+P(E_2) \cdot P(A \mid E_2)} \\ & =\frac{\frac{1}{2} \cdot \frac{1}{2}}{\frac{1}{2} \cdot \frac{1}{2}+\frac{1}{2} \cdot \frac{1}{4}} \\ & =\frac{\frac{1}{4}}{\frac{1}{4}+\frac{1}{8}} \\ & =\frac{\frac{1}{3}}{\frac{3}{8}} \\ & =\frac{2}{3} \end{aligned} $

3. Of the students in a college, it is known that $60 %$ reside in hostel and $40 %$ are day scholars (not residing in hostel). Previous year results report that $30 %$ of all students who reside in hostel attain A grade and $20 %$ of day scholars attain A grade in their annual examination. At the end of the year, one student is chosen at random from the college and he has an A grade, what is the probability that the student is a hostlier?

Solution

Let $E_1$ and $E_2$ be the events that the student is a hostler and a day scholar respectively and $A$ be the event that the chosen student gets grade $A$.

$\therefore P(E_1)=60 %=\frac{60}{100}=0.6$

$P(E_2)=40 %=\frac{40}{100}=0.4$

$P(A \mid E_1)=P$ (student getting an A grade is a hostler) $=30 %=0.3$

$P(A \mid E_2)=P($ student getting an A grade is a day scholar $)=20 %=0.2$

The probability that a randomly chosen student is a hostler, given that he has an A grade, is given by $P(E_1 \mid A)$.

By using Bayes’ theorem, we obtain

$ \begin{aligned} P(E_1 \mid A) & =\frac{P(E_1) \cdot P(A \mid E_1)}{P(E_1) \cdot P(A \mid E_1)+P(E_2) \cdot P(A \mid E_2)} \\ & =\frac{0.6 \times 0.3}{0.6 \times 0.3+0.4 \times 0.2} \\ & =\frac{0.18}{0.26} \\ & =\frac{18}{26} \\ & =\frac{9}{13} \end{aligned} $

4. In answering a question on a multiple choice test, a student either knows the answer or guesses. Let $\frac{3}{4}$ be the probability that he knows the answer and $\frac{1}{4}$ be the probability that he guesses. Assuming that a student who guesses at the answer will be correct with probability $\frac{1}{4}$. What is the probability that the student knows the answer given that he answered it correctly?

Solution

Let $E_1$ and $E_2$ be the respective events that the student knows the answer and he guesses the answer.

Let $A$ be the event that the answer is correct.

$\therefore P(E_1)=\frac{3}{4}$

$P(E_2)=\frac{1}{4}$

The probability that the student answered correctly, given that he knows the answer, is 1.

$\therefore P(A \mid E_1)=1$

Probability that the student answered correctly, given that he guessed, is $\frac{1}{4}$.

$\therefore P(A \mid E_2)=\frac{1}{4}$

The probability that the student knows the answer, given that he answered it correctly, is given by $P(E_1 \mid A)$

By using Bayes’ theorem, we obtain

$ \begin{aligned} P(E_1 \mid A) & =\frac{P(E_1) \cdot P(A \mid E_1)}{P(E_1) \cdot P(A \mid E_1)+P(E_2) \cdot P(A \mid E_2)} \\ & =\frac{\frac{3}{4} \cdot 1}{\frac{3}{4} \cdot 1+\frac{1}{4} \cdot \frac{1}{4}} \\ & =\frac{\frac{3}{4}}{\frac{3}{4}+\frac{1}{16}} \\ & =\frac{\frac{3}{13}}{\frac{16}{16}} \\ & =\frac{12}{13} \end{aligned} $

5. A laboratory blood test is $99 %$ effective in detecting a certain disease when it is in fact, present. However, the test also yields a false positive result for $0.5 %$ of the healthy person tested (i.e. if a healthy person is tested, then, with probability 0.005 , the test will imply he has the disease). If 0.1 percent of the population actually has the disease, what is the probability that a person has the disease given that his test result is positive?

Solution

Let $E_1$ and $E_2$ be the respective events that a person has a disease and a person has no disease.

Since $E_1$ and $E_2$ are events complimentary to each other,

$\therefore P(E_1)+P(E_2)=1$

$\Rightarrow P(E_2)=1-P(E_1)=1-0.001=0.999$

Let $A$ be the event that the blood test result is positive.

$P(E_1)=0.1 %=\frac{0.1}{100}=0.001$

$P(A \mid E_1)=P($ result is positive given the person has disease $)=99 %=0.99$

$P(A \mid E_2)=P($ result is positive given that the person has no disease $)=0.5 %=0.005$

Probability that a person has a disease, given that his test result is positive, is given by P $(E_1 \mid A)$.

By using Bayes’ theorem, we obtain

$ \begin{aligned} P(E_1 \mid A) & =\frac{P(E_1) \cdot P(A \mid E_1)}{P(E_1) \cdot P(A \mid E_1)+P(E_2) \cdot P(A \mid E_2)} \\ & =\frac{0.001 \times 0.99}{0.001 \times 0.99+0.999 \times 0.005} \\ & =\frac{0.00099}{0.00099+0.004995} \\ & =\frac{0.00099}{0.005985} \\ & =\frac{990}{5985} \\ & =\frac{110}{665} \\ & =\frac{22}{133} \end{aligned} $

6. There are three coins. One is a two headed coin (having head on both faces), another is a biased coin that comes up heads $75 %$ of the time and third is an unbiased coin. One of the three coins is chosen at random and tossed, it shows heads, what is the probability that it was the two headed coin?

Solution

Let $E_1, E_2$, and $E_3$ be the respective events of choosing a two headed coin, a biased coin, and an unbiased coin.

$\therefore P(E_1)=P(E_2)=P(E_3)=\frac{1}{3}$

Let $A$ be the event that the coin shows heads.

A two-headed coin will always show heads.

$\therefore P(A \mid E_1)=P($ coin showing heads, given that it is a two-headed coin $)=1$

Probability of heads coming up, given that it is a biased coin $=75 %$

$\therefore P(A \mid E_2)=P($ coin showing heads, given that it is a biased coin $)=\frac{75}{100}=\frac{3}{4}$

Since the third coin is unbiased, the probability that it shows heads is always $\frac{1}{2}$.

$\therefore P(A \mid E_3)=P($ coin showing heads, given that it is an unbiased coin $)=\frac{1}{2}$

The probability that the coin is two-headed, given that it shows heads, is given by $P(E_1 \mid A)$.

By using Bayes’ theorem, we obtain

$ \begin{aligned} P(E_1 \mid A) & =\frac{P(E_1) \cdot P(A \mid E_1)}{P(E_1) \cdot P(A \mid E_1)+P(E_2) \cdot P(A \mid E_2)+P(E_3) \cdot P(A \mid E_3)} \\ & =\frac{\frac{1}{3} \cdot 1}{\frac{1}{3} \cdot 1+\frac{1}{3} \cdot \frac{3}{4}+\frac{1}{3} \cdot \frac{1}{2}} \\ & =\frac{\frac{1}{3}}{\frac{1}{3}(1+\frac{3}{4}+\frac{1}{2})} \\ & =\frac{1}{\frac{9}{4}} \\ & =\frac{4}{9} \end{aligned} $

7. An insurance company insured 2000 scooter drivers, 4000 car drivers and 6000 truck drivers. The probability of an accidents are $0.01,0.03$ and 0.15 respectively. One of the insured persons meets with an accident. What is the probability that he is a scooter driver?

Solution

Let $E_1, E_2$, and $E_3$ be the respective events that the driver is a scooter driver, a car driver, and a truck driver.

Let $A$ be the event that the person meets with an accident.

There are 2000 scooter drivers, 4000 car drivers, and 6000 truck drivers.

Total number of drivers $=2000+4000+6000=12000$

$P(E_1)=P(.$ driver is a scooter driver) $=\frac{2000}{12000}=\frac{1}{6}$

$P(E_2)=P$ (driver is a car driver) $=\frac{4000}{12000}=\frac{1}{3}$

$P(E_3)=P(.$ driver is a truck driver) $=\frac{6000}{12000}=\frac{1}{2}$

$P(A \mid E_1)=P($ scooter driver met with an accident $)=0.01=\frac{1}{100}$

$P(A \mid E_2)=P($ car driver met with an accident $)=0.03=\frac{3}{100}$

$P(A \mid E_3)=P($ truck driver met with an accident $)=0.15=\frac{15}{100}$

The probability that the driver is a scooter driver, given that he met with an accident, is given by $P(E_1 \mid A)$.

By using Bayes’ theorem, we obtain

$ \begin{aligned} P(E_1 \mid A) & =\frac{P(E_1) \cdot P(A \mid E_1)}{P(E_1) \cdot P(A \mid E_1)+P(E_2) \cdot P(A \mid E_2)+P(E_3) \cdot P(A \mid E_3)} \\ & =\frac{\frac{1}{6} \cdot \frac{1}{100}}{\frac{1}{6} \cdot \frac{1}{100}+\frac{1}{3} \cdot \frac{3}{100}+\frac{1}{2} \cdot \frac{15}{100}} \\ & =\frac{\frac{1}{6} \cdot \frac{1}{100}}{\frac{1}{100}(\frac{1}{6}+1+\frac{15}{2})} \end{aligned} $

$ \begin{aligned} & =\frac{\frac{1}{6}}{\frac{104}{12}} \\ & =\frac{1}{6} \times \frac{12}{104} \\ & =\frac{1}{52} \end{aligned} $

8. A factory has two machines A and B. Past record shows that machine A produced $60 %$ of the items of output and machine B produced $40 %$ of the items. Further, $2 %$ of the items produced by machine $A$ and $1 %$ produced by machine $B$ were defective. All the items are put into one stockpile and then one item is chosen at random from this and is found to be defective. What is the probability that it was produced by machine $B$ ?

Solution

Let $E_1$ and $E_2$ be the respective events of items produced by machines $A$ and $B$. Let $X$ be the event that the produced item was found to be defective.

$\therefore$ Probability of items produced by machine $A, P(E_1)=60 %=\frac{3}{5}$

Probability of items produced by machine $B, P(E_2)=40 %=\frac{2}{5}$

Probability that machine A produced defective items, $P(X \mid E_1)=2 %=\frac{2}{100}$

Probability that machine $B$ produced defective items, $P(X \mid E_2)=1 %=\frac{1}{100}$

The probability that the randomly selected item was from machine $B$, given that it is defective, is given by $P(E_2 \mid X)$.

By using Bayes’ theorem, we obtain

$ \begin{aligned} P(E_2 \mid X) & =\frac{P(E_2) \cdot P(X \mid E_2)}{P(E_1) \cdot P(X \mid E_1)+P(E_2) \cdot P(X \mid E_2)} \\ & =\frac{\frac{2}{5} \cdot \frac{1}{100}}{\frac{3}{5} \cdot \frac{2}{100}+\frac{2}{5} \cdot \frac{1}{100}} \\ & =\frac{\frac{2}{500}}{\frac{6}{500}+\frac{2}{500}} \\ & =\frac{2}{8} \\ & =\frac{1}{4} \end{aligned} $

9. Two groups are competing for the position on the Board of directors of a corporation. The probabilities that the first and the second groups will win are 0.6 and 0.4 respectively. Further, if the first group wins, the probability of introducing a new product is 0.7 and the corresponding probability is 0.3 if the second group wins. Find the probability that the new product introduced was by the second group.

Solution

Let $E_1$ and $E_2$ be the respective events that the first group and the second group win the competition. Let $A$ be the event of introducing a new product.

$P(E_1)=$ Probability that the first group wins the competition $=0.6$

$P(E_2)=$ Probability that the second group wins the competition $=0.4$

$P(A \mid E_1)=$ Probability of introducing a new product if the first group wins $=0.7$

$P(A \mid E_2)=$ Probability of introducing a new product if the second group wins $=0.3$

The probability that the new product is introduced by the second group is given by $P(E_2 \mid A)$.

By using Bayes’ theorem, we obtain

$ \begin{aligned} P(E_2 \mid A) & =\frac{P(E_2) \cdot P(A \mid E_2)}{P(E_1) \cdot P(A \mid E_1)+P(E_2) \cdot P(A \mid E_2)} \\ & =\frac{0.4 \times 0.3}{0.6 \times 0.7+0.4 \times 0.3} \\ & =\frac{0.12}{0.42+0.12} \\ & =\frac{0.12}{0.54} \\ & =\frac{12}{54} \\ & =\frac{2}{9} \end{aligned} $

10. Suppose a girl throws a die. If she gets a 5 or 6 , she tosses a coin three times and notes the number of heads. If she gets $1,2,3$ or 4 , she tosses a coin once and notes whether a head or tail is obtained. If she obtained exactly one head, what is the probability that she threw $1,2,3$ or 4 with the die?

Solution

Let $E_1$ be the event that the outcome on the die is 5 or 6 and $E_2$ be the event that the outcome on the die is $1,2,3$, or 4 .

$\therefore P(E_1)=\frac{2}{6}=\frac{1}{3}$ and $P(E_2)=\frac{4}{6}=\frac{2}{3}$

Let $A$ be the event of getting exactly one head.

$P(A \mid E_1)=$ Probability of getting exactly one head by tossing the coin three times if she gets 5 or $6=\frac{3}{8}$

$P(A \mid E_2)=$ Probability of getting exactly one head in a single throw of coin if she gets 1 ,

2,3, or $4=\frac{1}{2}$

The probability that the girl threw $1,2,3$, or 4 with the die, if she obtained exactly one head, is given by $P(E_2 \mid A)$.

By using Bayes’ theorem, we obtain

$ \begin{aligned} P(E_2 \mid A) & =\frac{P(E_2) \cdot P(A \mid E_2)}{P(E_1) \cdot P(A \mid E_1)+P(E_2) \cdot P(A \mid E_2)} \\ & =\frac{\frac{2}{3} \cdot \frac{1}{2}}{\frac{1}{3} \cdot \frac{3}{8}+\frac{2}{3} \cdot \frac{1}{2}} \\ & =\frac{\frac{1}{3}}{\frac{1}{3}(\frac{3}{8}+1)} \\ & =\frac{1}{\frac{11}{8}} \\ & =\frac{8}{11} \end{aligned} $

11. A manufacturer has three machine operators $A, B$ and $C$. The first operator $A$ produces $1 %$ defective items, where as the other two operators $B$ and $C$ produce 5% and 7% defective items respectively. A is on the job for 50% of the time, B is on the job for $30 %$ of the time and $C$ is on the job for $20 %$ of the time. A defective item is produced, what is the probability that it was produced by A?

Solution

Let $E_1, E_2$ and $E_3$ be the respective events of the time consumed by machines $A, B$, and C for the job.

$ \begin{aligned} & P(E_1)=50 %=\frac{50}{100}=\frac{1}{2} \\ & P(E_2)=30 %=\frac{30}{100}=\frac{3}{10} \\ & P(E_3)=20 %=\frac{20}{100}=\frac{1}{5} \end{aligned} $

Let $X$ be the event of producing defective items.

$ \begin{aligned} & P(X \mid E_1)=1 %=\frac{1}{100} \\ & P(X \mid E_2)=5 %=\frac{5}{100} \\ & P(X \mid E_3)=7 %=\frac{7}{100} \end{aligned} $

The probability that the defective item was produced by $A$ is given by $P(E_1 \mid A)$.

By using Bayes’ theorem, we obtain

$ \begin{aligned} P(E_1 \mid X) & =\frac{P(E_1) \cdot P(X \mid E_1)}{P(E_1) \cdot P(X \mid E_1)+P(E_2) \cdot P(X \mid E_2)+P(E_3) \cdot P(X \mid E_3)} \\ & =\frac{\frac{1}{2} \cdot \frac{1}{100}}{\frac{1}{2} \cdot \frac{1}{100}+\frac{3}{10} \cdot \frac{5}{100}+\frac{1}{5} \cdot \frac{7}{100}} \\ & =\frac{\frac{1}{100} \cdot \frac{1}{2}}{\frac{1}{100}(\frac{1}{2}+\frac{3}{2}+\frac{7}{5})} \\ & =\frac{\frac{1}{17}}{\frac{5}{5}} \\ & =\frac{5}{34} \end{aligned} $

12. A card from a pack of 52 cards is lost. From the remaining cards of the pack, two cards are drawn and are found to be both diamonds. Find the probability of the lost card being a diamond.

Solution

Let $E_1$ and $E_2$ be the respective events of choosing a diamond card and a card which is not diamond.

Let $A$ denote the lost card.

Out of 52 cards, 13 cards are diamond and 39 cards are not diamond. $\therefore P(E_1)=\frac{13}{52}=\frac{1}{4}$

$P(E_2)=\frac{39}{52}=\frac{3}{4}$

When one diamond card is lost, there are 12 diamond cards out of 51 cards.

Two cards can be drawn out of 12 diamond cards in ${ }^{12} C_2$ ways.

Similarly, 2 diamond cards can be drawn out of 51 cards in ${ }^{51} C_2$ ways. The probability of getting two cards, when one diamond card is lost, is given by $P(A \mid E_1)$.

$P(A \mid E_1)=\frac{{ }^{12} C_2}{{ }^{51} C_2}=\frac{12 !}{2 ! 10 !} \times \frac{21 \times 49 !}{51 !}=\frac{11 \times 12}{50 \times 51}=\frac{22}{425}$

When the lost card is not a diamond, there are 13 diamond cards out of 51 cards.

Two cards can be drawn out of 13 diamond cards in ${ }^{13} C_2$ ways whereas 2 cards can be drawn out of 51 cards in ${ }^{51} C_2$ ways.

The probability of getting two cards, when one card is lost which is not diamond, is given by $P(A \mid E_2)$.

$ P(A \mid E_2)=\frac{{ }^{13} C_2}{{ }^{51} C_2}=\frac{13 !}{2 ! \times 11 !} \times \frac{2 ! \times 49 !}{51 !}=\frac{12 \times 13}{50 \times 51}=\frac{26}{425} $

The probability that the lost card is diamond is given by $P(E_1 \mid A)$.

By using Bayes’ theorem, we obtain

$ \begin{aligned} P(E_1 \mid A) & =\frac{P(E_1) \cdot P(A \mid E_1)}{P(E_1) \cdot P(A \mid E_1)+P(E_2) \cdot P(A \mid E_2)} \\ & =\frac{\frac{1}{4} \cdot \frac{22}{425}}{\frac{1}{4} \cdot \frac{22}{425}+\frac{3}{4} \cdot \frac{26}{425}} \\ & =\frac{\frac{1}{425}(\frac{22}{4})}{\frac{1}{425}(\frac{22}{4}+\frac{26 \times 3}{4})} \end{aligned} $

$ \begin{matrix} =\frac{\frac{11}{2}}{25} \\ =\frac{11}{50} \end{matrix} $

13. Probability that A speaks truth is $\frac{4}{5}$. A coin is tossed. A reports that a head appears. The probability that actually there was head is (A) $\frac{4}{5}$ (B) $\frac{1}{2}$ (C) $\frac{1}{5}$ (D) $\frac{2}{5}$

Solution

Let $E_1$ and $E_2$ be the events such that

$E_1:$ A speaks truth

$E_2$ : A speaks false

Let $X$ be the event that a head appears.

$P(E_1)=\frac{4}{5}$

$\therefore P(E_2)=1-P(E_1)=1-\frac{4}{5}=\frac{1}{15}$

If a coin is tossed, then it may result in either head $(H)$ or tail $(T)$.

The probability of getting a head is $\frac{1}{2}$ whether A speaks truth or not.

$\therefore P(X \mid E_1)=P(X \mid E_2)=\frac{1}{2}$

The probability that there is actually a head is given by $P(E_1 \mid X)$.

$ \begin{aligned} P(E_1 \mid X) & =\frac{P(E_1) \cdot P(X \mid E_1)}{P(E_1) \cdot P(X \mid E_1)+P(E_2) \cdot P(X \mid E_2)} \\ & =\frac{\frac{4}{5} \cdot \frac{1}{2}}{\frac{4}{5} \cdot \frac{1}{2}+\frac{1}{5} \cdot \frac{1}{2}} \\ & =\frac{\frac{1}{2} \cdot \frac{4}{5}}{\frac{1}{2}(\frac{4}{5}+\frac{1}{5})} \\ & =\frac{4}{\frac{5}{1}} \\ & =\frac{4}{5} \end{aligned} $

Therefore, the correct answer is A.

14. If $A$ and $B$ are two events such that $A \subset B$ and $P(B) \neq 0$, then which of the following is correct? (A) $P(A \mid B)=\frac{P(B)}{P(A)}$ (B) $P(A \mid B)<P(A)$ (C) $P(A \mid B) \geq P(A)$ (D) None of these

Solution

If $A \subset B$, then $A \cap B=A$ $\Rightarrow P(A \cap B)=P(A)$

Also, $P(A)<P(B)$

Consider $P(A \mid B)=\frac{P(A \cap B)}{P(B)}=\frac{P(A)}{P(B)} \neq \frac{P(B)}{P(A)} \ldots$ (1)

Consider $P(A \mid B)=\frac{P(A \cap B)}{P(B)}=\frac{P(A)}{P(B)} \ldots$ (2)

It is known that, $P(B) \leq 1$

$\Rightarrow \frac{1}{P(B)} \geq 1$

$\Rightarrow \frac{P(A)}{P(B)} \geq P(A)$

From (2), we obtain

$\Rightarrow P(A \mid B) \geq P(A)$

$\therefore P(A \mid B)$ is not less than $P(A)$.

Thus, from (3), it can be concluded that the relation given in alternative $C$ is correct.

Miscellaneous Examples

Example 22 Coloured balls are distributed in four boxes as shown in the following table:

Box	Colour
I	3	4	5	6
II	2	2	2	2
III	1	2	3	1
IV	4	3	1	5

A box is selected at random and then a ball is randomly drawn from the selected box. The colour of the ball is black, what is the probability that ball drawn is from the box III?

Solution Let $A, E_1, E_2, E_3$ and $E_4$ be the events as defined below :

$ \begin{matrix} A: \text{ a black ball is selected } & E_1: \text{ box I is selected } \\ E_2: \text{ box II is selected } & E_3: \text{ box III is selected } \\ E_4: \text{ box IV is selected } & \end{matrix} $

Since the boxes are chosen at random,

Therefore

$ P(E_1)=P(E_2)=P(E_3)=P(E_4)=\frac{1}{4} $

Also

$ P(AlE E_1)=\frac{3}{18}, P(AlE_2)=\frac{2}{8}, P(AlE_3)=\frac{1}{7} \text{ and } P(AlE_4)=\frac{4}{13} $

$P($ box III is selected, given that the drawn ball is black $)=P(E_3 \mid A)$. By Bayes’ theorem,

$ \begin{aligned} P(E_3 \mid A) & =\frac{P(E_3) \cdot P(AlE_3)}{P(E_1) P(Al E_1)+P(E_2) P(AlE_2)+P(E_3) P(AlE_3)+P(E_4) P(AlE_4)} \\ & =\frac{\frac{1}{4} \times \frac{1}{7}}{\frac{1}{4} \times \frac{3}{18}+\frac{1}{4} \times \frac{1}{4}+\frac{1}{4} \times \frac{1}{7}+\frac{1}{4} \times \frac{4}{13}}=0.165 \end{aligned} $

Example 23 $A$ and $B$ throw a die alternatively till one of them gets a ’ 6 ’ and wins the game. Find their respective probabilities of winning, if A starts first.

Solution Let S denote the success (getting a ’ 6 ‘) and $F$ denote the failure (not getting a ’ 6 ‘).

Thus,

$ P(S)=\frac{1}{6}, P(F)=\frac{5}{6} $

$P(A$ wins in the first throw $)=P(S)=\frac{1}{6}$

A gets the third throw, when the first throw by $A$ and second throw by $B$ result into failures.

Therefore, $\quad P(A$ wins in the 3rd throw $)=P(FFS)=P(F) P(F) P(S)=\frac{5}{6} \times \frac{5}{6} \times \frac{1}{6}$

$ =(\frac{5}{6})^{2} \times \frac{1}{6} $

$P(A$ wins in the 5 th throw $)=P($ FFFFS $)=(\frac{5}{6})^{4}(\frac{1}{6})$ and so on.

Hence,

$ \begin{aligned} P(\text{ A wins }) & =\frac{1}{6}+(\frac{5}{6})^{2}(\frac{1}{6})+(\frac{5}{6})^{4}(\frac{1}{6})+\ldots \\ & =\frac{\frac{1}{6}}{1-\frac{25}{36}}=\frac{6}{11} \\ P(B \text{ wins }) & =1-P(\text{ A wins })=1-\frac{6}{11}=\frac{5}{11} \end{aligned} $

Remark If $a+a r+a r^{2}+\ldots+a r^{n-1}+\ldots$, where $|r|<1$, then sum of this infinite G.P. is given by $\frac{a}{1-r} \cdot($ Refer A.1.3 of Class XI Text book).

Example 24 If a machine is correctly set up, it produces $90 %$ acceptable items. If it is incorrectly set up, it produces only $40 %$ acceptable items. Past experience shows that $80 %$ of the set ups are correctly done. If after a certain set up, the machine produces 2 acceptable items, find the probability that the machine is correctly setup.

Solution Let A be the event that the machine produces 2 acceptable items.

Also let $B_1$ represent the event of correct set up and $B_2$ represent the event of incorrect setup.

Now

$ P(B_1)=0.8, P(B_2)=0.2 $

$ P(AlB_1)=0.9 \times 0.9 \text{ and } P(AlB_2)=0.4 \times 0.4 $

Therefore

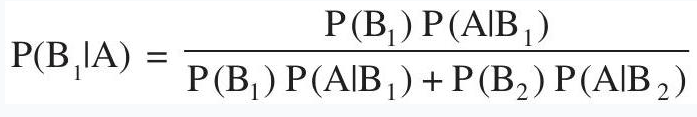
$ \begin{aligned} & =\frac{0.8 \times 0.9 \times 0.9}{0.8 \times 0.9 \times 0.9+0.2 \times 0.4 \times 0.4}=\frac{648}{680}=0.95 \end{aligned} $

Miscellaneous Exercise on Chapter 13

1. $A$ and $B$ are two events such that $P(A) \neq 0$. Find $P(B \mid A)$, if (i) $A$ is a subset of $B$ (ii) $A \cap B=\phi$

Solution

It is given that, $P(A) \neq 0$

(i) $A$ is a subset of $B$.

$\Rightarrow A \cap B=A$

$\therefore P(A \cap B)=P(B \cap A)=P(A)$

$\therefore P(B \mid A)=\frac{P(B \cap A)}{P(A)}=\frac{P(A)}{P(A)}=1$

(ii) $A \cap B=\phi$

$\Rightarrow P(A \cap B)=0$

$\therefore P(B \mid A)=\frac{P(A \cap B)}{P(A)}=0$

2. A couple has two children,

(i) Find the probability that both children are males, if it is known that at least one of the children is male.

(ii) Find the probability that both children are females, if it is known that the elder child is a female.

Solution

If a couple has two children, then the sample space is

$S={(b, b),(b, g),(g, b),(g, g)}$

(i) Let $E$ and $F$ respectively denote the events that both children are males and at least one of the children is a male. $\therefore E \cap F={(b, b)} \Rightarrow P(E \cap F)=\frac{1}{4}$

$P(E)=\frac{1}{4}$

$P(F)=\frac{3}{4}$

$\Rightarrow P(E \mid F)=\frac{P(E \cap F)}{P(F)}=\frac{\frac{1}{4}}{\frac{3}{4}}=\frac{1}{3}$

(ii) Let $A$ and $B$ respectively denote the events that both children are females and the elder child is a female.

$ \begin{aligned} & A={(g, g)} \Rightarrow P(A)=\frac{1}{4} \\ & B={(g, b),(g, g)} \Rightarrow P(B)=\frac{2}{4} \\ & A \cap B={(g, g)} \Rightarrow P(A \cap B)=\frac{1}{4} \\ & P(A \mid B)=\frac{P(A \cap B)}{P(B)}=\frac{\frac{1}{2}}{\frac{2}{4}}=\frac{1}{2} \end{aligned} $

3. Suppose that $5 %$ of men and $0.25 %$ of women have grey hair. A grey haired person is selected at random. What is the probability of this person being male? Assume that there are equal number of males and females.

Solution

It is given that $5 %$ of men and $0.25 %$ of women have grey hair.

Therefore, percentage of people with grey hair $=(5+0.25) %=5.25 %$

$\square$ Probability that the selected haired person is a male $=\frac{5}{5.25}=\frac{20}{21}$

4. Suppose that $90 %$ of people are right-handed. What is the probability that at most 6 of a random sample of 10 people are right-handed?

Solution

A person can be either right-handed or left-handed.

It is given that $90 %$ of the people are right-handed.

$\therefore p=P($ right-handed $)=\frac{9}{10}$

$q=P($ left-handed $)=1-\frac{9}{10}=\frac{1}{10}$

Using binomial distribution, the probability that more than 6 people are right-handed is given by,

$\sum _{r=7}^{10}{ }^{10} C_r p^{r} q^{n-r}=\sum _{r=7}^{10}{ }^{10} C_r(\frac{9}{10})^{r}(\frac{1}{10})^{10-r}$

Therefore, the probability that at most 6 people are right-handed

$=1-P$ (more than 6 are right-handed)

$=1-\sum _{r=7}^{10}{ }^{10} C_r(0.9)^{r}(0.1)^{10-r}$

5. If a leap year is selected at random, what is the chance that it will contain 53 tuesdays?

Solution

In a leap year, there are 366 days i.e., 52 weeks and 2 days.

In 52 weeks, there are 52 Tuesdays.

Therefore, the probability that the leap year will contain 53 Tuesdays is equal to the probability that the remaining 2 days will be Tuesdays.

The remaining 2 days can be

Monday and Tuesday

Tuesday and Wednesday

Wednesday and Thursday

Thursday and Friday

Friday and Saturday

Saturday and Sunday

Sunday and Monday

Total number of cases $=7$

Favourable cases $=2$

$\square$ Probability that a leap year will have 53 Tuesdays $=\frac{2}{7}$

6. Suppose we have four boxes A,B,C and D containing coloured marbles as given below:

Box	Marble colour
	1	6	3
A	6	2	2
B	8	1	1
C	8	1	1
D	0	6	4

One of the boxes has been selected at random and a single marble is drawn from it. If the marble is red, what is the probability that it was drawn from box A?, box B?, box $C$ ?

Solution

Let $R$ be the event of drawing the red marble.

Let $E_A, E_B$, and $E_C$ respectively denote the events of selecting the box $A, B$, and $C$.

Total number of marbles $=40$

Number of red marbles $=15$

$\therefore P(R)=\frac{15}{40}=\frac{3}{8}$

Probability of drawing the red marble from box $A$ is given by $P(E_A \mid R)$.

$\therefore P(E_A \mid R)=\frac{P(E_A \cap R)}{P(R)}=\frac{\frac{1}{40}}{\frac{3}{8}}=\frac{1}{15}$

Probability that the red marble is from box $B$ is $P(E_B \mid R)$.

$\Rightarrow P(E_B \mid R)=\frac{P(E_B \cap R)}{P(R)}=\frac{\frac{6}{40}}{\frac{3}{8}}=\frac{2}{5}$

Probability that the red marble is from box $C$ is $P(E_C \mid R)$.

$\Rightarrow P(E_C \mid R)=\frac{P(E_C \cap R)}{P(R)}=\frac{\frac{8}{40}}{\frac{3}{8}}=\frac{8}{15}$

7. Assume that the chances of a patient having a heart attack is $40 %$. It is also assumed that a meditation and yoga course reduce the risk of heart attack by $30 %$ and prescription of certain drug reduces its chances by $25 %$. At a time a patient can choose any one of the two options with equal probabilities. It is given that after going through one of the two options the patient selected at random suffers a heart attack. Find the probability that the patient followed a course of meditation and yoga?

Solution

Let $A, E_1$, and $E_2$ respectively denote the events that a person has a heart attack, the selected person followed the course of yoga and meditation, and the person adopted the drug prescription.

$\therefore P(A)=0.40$

$P(E_1)=P(E_2)=\frac{1}{2}$

$P(A \mid E_1)=0.40 \times 0.70=0.28$

$P(A \mid E_2)=0.40 \times 0.75=0.30$

Probability that the patient suffering a heart attack followed a course of meditation and yoga is given by $P(E_1 \mid A)$.

$ \begin{aligned} P(E_1 \mid A) & =\frac{P(E_1) P(A \mid E_1)}{P(E_1) P(A \mid E_1)+P(E_2) P(A \mid E_2)} \\ & =\frac{\frac{1}{2} \times 0.28}{\frac{1}{2} \times 0.28+\frac{1}{2} \times 0.30} \\ & =\frac{14}{29} \end{aligned} $

8. If each element of a second order determinant is either zero or one, what is the probability that the value of the determinant is positive? (Assume that the individual entries of the determinant are chosen independently, each value being assumed with probability $\frac{1}{2}$ ).

Solution

The total number of determinants of second order with each element being 0 or 1 is (2) $=16$

The value of determinant is positive in the following cases. $ \begin{vmatrix} 1 & 0 \\ 0 & 1\end{vmatrix} \begin{vmatrix} 1 & 1 \\ 0 & 1\end{vmatrix} \begin{vmatrix} 1 & 0 \\ 1 & 1\end{vmatrix} $

$\square$ Required probability $=\frac{3}{16}$

9. An electronic assembly consists of two subsystems, say, A and B. From previous testing procedures, the following probabilities are assumed to be known:

$ \begin{aligned} P(A \text{ fails }) & =0.2 \\ P(B \text{ fails alone }) & =0.15 \\ P(A \text{ and } B \text{ fail }) & =0.15 \end{aligned} $

Evaluate the following probabilities (i) $P$ (A fails $\mid B$ has failed) (ii) $P$ (A fails alone)

Solution

Let the event in which $A$ fails and $B$ fails be denoted by $E_A$ and $E_B$.

$P(E_A)=0.2$

$P(E_A \square E_B)=0.15$

$P(B$ fails alone $)=P(E_B)-P(E_A \square E_B)$

$\square 0.15=P(E_B)-0.15$

$\square P(E_B)=0.3$

(i) $P(E_A \mid E_B)=\frac{P(E_A \cap E_B)}{P(E_B)}=\frac{0.15}{0.3}=0.5$

(ii) $P(A$ fails alone $)=P(E_A)-P(E_A \square E_B)$

$=0.2-0.15$

$=0.05$

10. Bag I contains 3 red and 4 black balls and Bag II contains 4 red and 5 black balls. One ball is transferred from Bag I to Bag II and then a ball is drawn from Bag II. The ball so drawn is found to be red in colour. Find the probability that the transferred ball is black.

Solution

Let $E_1$ and $E_2$ respectively denote the events that a red ball is transferred from bag I to II and a black ball is transferred from bag I to II.

$P(E_1)=\frac{3}{7}$ and $P(E_2)=\frac{4}{7}$

Let $A$ be the event that the ball drawn is red.

When a red ball is transferred from bag I to II,

$P(A \mid E_1)=\frac{5}{10}=\frac{1}{2}$

When a black ball is transferred from bag I to II,

$P(A \mid E_2)=\frac{4}{10}=\frac{2}{5}$

$ \begin{aligned} \therefore P(E_2 \mid A) & =\frac{P(E_2) P(A \mid E_2)}{P(E_1) P(A \mid E_1)+P(E_2) P(A \mid E_2)} \\ & =\frac{\frac{4}{7} \times \frac{2}{5}}{\frac{3}{7} \times \frac{1}{2}+\frac{4}{7} \times \frac{2}{5}} \\ & =\frac{16}{31} \end{aligned} $

Choose the correct answer in each of the following:

11. If $A$ and $B$ are two events such that $P(A) \neq 0$ and $P(B \mid A)=1$, then (A) $A \subset B$ (B) $B \subset A$ (C) $B=\phi$ (D) $A=\phi$

Solution

$P(A) \neq 0$ and $P(B \mid A)=1$

$P(B \mid A)=\frac{P(B \cap A)}{P(A)}$

$l=\frac{P(B \cap A)}{P(A)}$

$P(A)=P(B \cap A)$

$\Rightarrow A \subset B$

Thus, the correct answer is $A$.

12. If $P(A \mid B)>P(A)$, then which of the following is correct : (A) $P(B \mid A)<P(B)$ (B) $P(A \cap B)<P(A) \cdot P(B)$ (C) $P(B \mid A)>P(B)$ (D) $P(B \mid A)=P(B)$

Solution

$ \begin{aligned} & P(A \mid B)>P(A) \\ & \Rightarrow \frac{P(A \cap B)}{P(B)}>P(A) \\ & \Rightarrow P(A \cap B)>P(A) \cdot P(B) \\ & \Rightarrow \frac{P(A \cap B)}{P(A)}>P(B) \\ & \Rightarrow P(B \mid A)>P(B) \end{aligned} $

Thus, the correct answer is $C$.

13. If $A$ and $B$ are any two events such that $P(A)+P(B)-P(A$ and $B)=P(A)$, then (A) $P(B \mid A)=1$ (B) $P(A \mid B)=1$ (C) $P(B \mid A)=0$ (D) $P(A \mid B)=0$

Solution

$ \begin{aligned} & P(A)+P(B)-P(A \text{ and } B)=P(A) \\ & \Rightarrow P(A)+P(B)-P(A \cap B)=P(A) \\ & \Rightarrow P(B)-P(A \cap B)=0 \\ & \Rightarrow P(A \cap B)=P(B) \\ & \therefore P(A \mid B)=\frac{P(A \cap B)}{P(B)}=\frac{P(B)}{P(B)}=1 \end{aligned} $

Thus, the correct answer is B.

Summary

The salient features of the chapter are -

The conditional probability of an event $E$, given the occurrence of the event $F$ is given by $P(E \mid F)=\frac{P(E \cap F)}{P(F)}, P(F) \neq 0$

$\Delta 0 \leq P(E \mid F) \leq 1, \quad P(E^{\prime} \mid F)=1-P(E \mid F)$

$P((E \cup F) \mid G)=P(E \mid G)+P(F \mid G)-P((E \cap F) \mid G)$

$\Delta P(E \cap F)=P(E) P(F \mid E), P(E) \neq 0$

$P(E \cap F)=P(F) P(EIF), P(F) \neq 0$

$\checkmark$ If $E$ and $F$ are independent, then

$P(E \cap F)=P(E) P(F)$

$P(EIF)=P(E), P(F) \neq 0$

$P(F \mid E)=P(F), P(E) \neq 0$

- Theorem of total probability

Let ${E_1, E_2, \ldots, E_n)$ be a partition of a sample space and suppose that each of $E_1, E_2, \ldots, E_n$ has nonzero probability. Let $A$ be any event associated with $S$, then

$P(A)=P(E_1) P(AlE_1)+P(E_2) P(AlE_2)+\ldots+P(E_n) P(AlE_n)$

Bayes’ theorem If $E_1, E_2, \ldots, E_n$ are events which constitute a partition of sample space $S$, i.e. $E_1, E_2, \ldots, E_n$ are pairwise disjoint and $E_1 \cup E_2 \cup \ldots \cup E_n=S$ and $A$ be any event with nonzero probability, then

$ P(E_i \mid A)=\frac{P(E_i) P(A \mid E_i)}{\sum _{j=1}^{n} P(E_j) P(A \mid E_j)} $

Historical Note

The earliest indication on measurement of chances in game of dice appeared in 1477 in a commentary on Dante’s Divine Comedy. A treatise on gambling named liber de Ludo Alcae, by Geronimo Carden (1501-1576) was published posthumously in 1663 . In this treatise, he gives the number of favourable cases for each event when two dice are thrown.

Galileo (1564-1642) gave casual remarks concerning the correct evaluation of chance in a game of three dice. Galileo analysed that when three dice are thrown, the sum of the number that appear is more likely to be 10 than the sum 9 , because the number of cases favourable to 10 are more than the number of cases for the appearance of number 9.

Apart from these early contributions, it is generally acknowledged that the true origin of the science of probability lies in the correspondence between two great men of the seventeenth century, Pascal (1623-1662) and Pierre de Fermat (1601-1665). A French gambler, Chevalier de Metre asked Pascal to explain some seeming contradiction between his theoretical reasoning and the observation gathered from gambling. In a series of letters written around 1654, Pascal and Fermat laid the first foundation of science of probability. Pascal solved the problem in algebraic manner while Fermat used the method of combinations.

Great Dutch Scientist, Huygens (1629-1695), became acquainted with the content of the correspondence between Pascal and Fermat and published a first book on probability, “De Ratiociniis in Ludo Aleae” containing solution of many interesting rather than difficult problems on probability in games of chances.

The next great work on probability theory is by Jacob Bernoulli (1654-1705), in the form of a great book, “Ars Conjectendi” published posthumously in 1713 by his nephew, Nicholes Bernoulli. To him is due the discovery of one of the most important probability distribution known as Binomial distribution. The next remarkable work on probability lies in 1993. A. N. Kolmogorov (1903-1987) is credited with the axiomatic theory of probability. His book, ‘Foundations of probability’ published in 1933, introduces probability as a set function and is considered a ‘classic!’.