THREE DIMENSIONAL GEOMETRY

The moving power of mathematical invention is not reasoning but imagination. - A.DEMORGAN

Introduction

In Class XI, while studying Analytical Geometry in two dimensions, and the introduction to three dimensional geometry, we confined to the Cartesian methods only. In the previous chapter of this book, we have studied some basic concepts of vectors. We will now use vector algebra to three dimensional geometry. The purpose of this approach to 3-dimensional geometry is that it makes the study simple and elegant*.

In this chapter, we shall study the direction cosines and direction ratios of a line joining two points and also discuss about the equations of lines and planes in space under different conditions, angle between two lines, two planes, a line and a plane, shortest distance between two skew lines and distance of a point from a plane. Most of

Leonhard Euler $(\mathbf{1 7 0 7 - 1 7 8 3 })$ the above results are obtained in vector form. Nevertheless, we shall also translate these results in the Cartesian form which, at times, presents a more clear geometric and analytic picture of the situation.

Direction Cosines and Direction Ratios of a Line

From Chapter 10, recall that if a directed line $L$ passing through the origin makes angles $\alpha, \beta$ and $\gamma$ with $x, y$ and $z$-axes, respectively, called direction angles, then cosine of these angles, namely, $\cos \alpha, \cos \beta$ and $\cos \gamma$ are called direction cosines of the directed line $L$.

If we reverse the direction of $L$, then the direction angles are replaced by their supplements, i.e., $\pi-\alpha, \pi-\beta$ and $\pi-\gamma$. Thus, the signs of the direction cosines are reversed. \footnotetext{

• For various activities in three dimensional geometry, one may refer to the Book “A Hand Book for designing Mathematics Laboratory in Schools”, NCERT, 2005 }

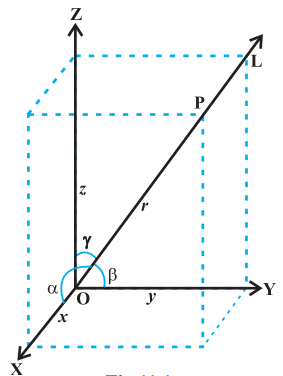
Fig 11.1

Note that a given line in space can be extended in two opposite directions and so it has two sets of direction cosines. In order to have a unique set of direction cosines for a given line in space, we must take the given line as a directed line. These unique direction cosines are denoted by $l, m$ and $n$.

Remark If the given line in space does not pass through the origin, then, in order to find its direction cosines, we draw a line through the origin and parallel to the given line. Now take one of the directed lines from the origin and find its direction cosines as two parallel line have same set of direction cosines.

Any three numbers which are proportional to the direction cosines of a line are called the direction ratios of the line. If $l, m, n$ are direction cosines and $a, b, c$ are direction ratios of a line, then $a=\lambda l, b=\lambda m$ and $c=\lambda n$, for any nonzero $\lambda \in \mathbf{R}$.

5 Note Some authors also call direction ratios as direction numbers.

Let $a, b, c$ be direction ratios of a line and let $l, m$ and $n$ be the direction cosines (d.c’s) of the line. Then

$$ \frac{l}{a}=\frac{m}{b}=\frac{n}{c}=k \text{ (say), } k \text{ being a constant. } $$

Therefore

$$ l=a k, m=b k, n=c k $$

But

Therefore

$$ l^{2}+m^{2}+n^{2}=1 $$

$$ k^{2}(a^{2}+b^{2}+c^{2})=1 $$

or

$$ k= \pm \frac{1}{\sqrt{a^{2}+b^{2}+c^{2}}} $$

Hence, from (1), the d.c.’s of the line are

$$ l= \pm \frac{a}{\sqrt{a^{2}+b^{2}+c^{2}}}, m= \pm \frac{b}{\sqrt{a^{2}+b^{2}+c^{2}}}, n= \pm \frac{c}{\sqrt{a^{2}+b^{2}+c^{2}}} $$s

where, depending on the desired sign of $k$, either a positive or a negative sign is to be taken for $l, m$ and $n$.

For any line, if $a, b, c$ are direction ratios of a line, then $k a, k b, k c ; k \neq 0$ is also a set of direction ratios. So, any two sets of direction ratios of a line are also proportional. Also, for any line there are infinitely many sets of direction ratios.

Direction cosines of a line passing through two points

Since one and only one line passes through two given points, we can determine the direction cosines of a line passing through the given points $P(x_1, y_1, z_1)$ and $Q(x_2, y_2, z_2)$ as follows (Fig 11.2 (a)).

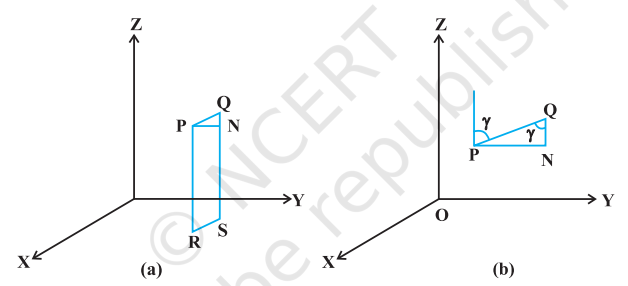
Fig 11.2

Let $l, m, n$ be the direction cosines of the line PQ and let it makes angles $\alpha, \beta$ and $\gamma$ with the $x, y$ and $z$-axis, respectively.

Draw perpendiculars from $P$ and $Q$ to $XY$-plane to meet at $R$ and $S$. Draw a perpendicular from $P$ to $QS$ to meet at $N$. Now, in right angle triangle $PNQ, \angle PQN=\gamma$ (Fig 11.2 (b)).

Therefore, $$\quad \cos \gamma=\frac{NQ}{PQ}=\frac{z_2-z_1}{PQ}$$

Similarly

$$ \cos \alpha=\frac{x_2-x_1}{PQ} \text{ and } \cos \beta=\frac{y_2-y_1}{PQ} $$

Hence, the direction cosines of the line segment joining the points $P(x_1, y_1, z_1)$ and $Q(x_2, y_2, z_2)$ are

$$ \frac{x_2-x_1}{PQ}, \frac{y_2-y_1}{PQ}, \frac{z_2-z_1}{PQ} $$

where

$$ PQ=\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}+(z_2-z_1)^{2}} $$

Note The direction ratios of the line segment joining $P(x_1, y_1, z_1)$ and $Q(x_2, y_2, z_2)$ may be taken as

$$ x_2-x_1, y_2-y_1, z_2-z_1 \text{ or } x_1-x_2, y_1-y_2, z_1-z_2 $$

Example 1 If a line makes angle $90^{\circ}, 60^{\circ}$ and $30^{\circ}$ with the positive direction of $x, y$ and $z$-axis respectively, find its direction cosines.

Solution Let the $d . c$. ’ $s$ of the lines be $l, m, n$. Then $l=\cos 90^{\circ}=0, m=\cos 60^{\circ}=\frac{1}{2}$,

$n=\cos 30^{\circ}=\frac{\sqrt{3}}{2}$.

Example 2 If a line has direction ratios 2, - 1, - 2, determine its direction cosines.

Solution Direction cosines are

$$ \frac{2}{\sqrt{2^{2}+(-1)^{2}+(-2)^{2}}}, \frac{-1}{\sqrt{2^{2}+(-1)^{2}+(-2)^{2}}}, \frac{-2}{\sqrt{2^{2}+(-1)^{2}+(-2)^{2}}} $$

or $$\frac{2}{3}, \frac{-1}{3}, \frac{-2}{3}$$

Example 3 Find the direction cosines of the line passing through the two points $(-2,4,-5)$ and $(1,2,3)$.

Solution We know the direction cosines of the line passing through two points $P(x_1, y_1, z_1)$ and $Q(x_2, y_2, z_2)$ are given by

where

$$ \frac{x_2-x_1}{PQ}, \frac{y_2-y_1}{PQ}, \frac{z_2-z_1}{PQ} $$

$$ PQ=\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}+(z_2-z_1)^{2}} $$

Here $P$ is $(-2,4,-5)$ and $Q$ is $(1,2,3)$.

So

$$ P Q=\sqrt{(1-(-2))^{2}+(2-4)^{2}+(3-(-5))^{2}}=\sqrt{77} $$

Thus, the direction cosines of the line joining two points is

$$ \frac{3}{\sqrt{77}}, \frac{-2}{\sqrt{77}}, \frac{8}{\sqrt{77}} $$

Example 4 Find the direction cosines of $x, y$ and $z$-axis.

Solution The $x$-axis makes angles $0^{\circ}, 90^{\circ}$ and $90^{\circ}$ respectively with $x, y$ and $z$-axis. Therefore, the direction cosines of $x$-axis are $\cos 0^{\circ}, \cos 90^{\circ}, \cos 90^{\circ}$ i.e., $1,0,0$. Similarly, direction cosines of $y$-axis and $z$-axis are $0,1,0$ and $0,0,1$ respectively.

Example 5 Show that the points A $(2,3,-4), B(1,-2,3)$ and $C(3,8,-11)$ are collinear.

Solution Direction ratios of line joining A and B are

$1-2,-2-3,3+4$ i.e., $-1,-5,7$.

The direction ratios of line joining $B$ and $C$ are

$3-1,8+2,-11-3$, i.e., $2,10,-14$.

It is clear that direction ratios of $AB$ and $BC$ are proportional, hence, $AB$ is parallel to $BC$. But point $B$ is common to both $AB$ and $BC$. Therefore, $A, B, C$ are collinear points.

EXERCISE 11.1

1. If a line makes angles $90^{\circ}, 135^{\circ}, 45^{\circ}$ with the $x, y$ and $z$-axes respectively, find its direction cosines.

Solution

Let direction cosines of the line be $l, m$, and $n$.

$l=\cos 90^{\circ}=0$

$m=\cos 135^{\circ}=-\frac{1}{\sqrt{2}}$

$n=\cos 45^{\circ}=\frac{1}{\sqrt{2}}$

Therefore, the direction cosines of the line are $0,-\frac{1}{\sqrt{2}}$, and $\frac{1}{\sqrt{2}}$.

2. Find the direction cosines of a line which makes equal angles with the coordinate axes.

Solution

Let the direction cosines of the line make an angle $a$ with each of the coordinate axes.

$\therefore I=\cos a, m=\cos a, n=\cos a$

$ \begin{aligned} & l^{2}+m^{2}+n^{2}=1 \\ & \Rightarrow \cos ^{2} \alpha+\cos ^{2} \alpha+\cos ^{2} \alpha=1 \\ & \Rightarrow 3 \cos ^{2} \alpha=1 \\ & \Rightarrow \cos ^{2} \alpha=\frac{1}{3} \\ & \Rightarrow \cos \alpha= \pm \frac{1}{\sqrt{3}} \end{aligned} $

Thus, the direction cosines of the line, which is equally inclined to the coordinate axes,

are $\pm \frac{1}{\sqrt{3}}, \pm \frac{1}{\sqrt{3}}$, and $\pm \frac{1}{\sqrt{3}}$.

3. If a line has the direction ratios $-18,12,-4$, then what are its direction cosines?

Solution

If a line has direction ratios of $-18,12$, and -4 , then its direction cosines are

$\frac{-18}{\sqrt{(-18)^{2}+(12)^{2}+(-4)^{2}}}, \frac{12}{\sqrt{(-18)^{2}+(12)^{2}+(-4)^{2}}}, \frac{-4}{\sqrt{(-18)^{2}+(12)^{2}+(-4)^{2}}}$

i.e., $\frac{-18}{22}, \frac{12}{22}, \frac{-4}{22}$

$\frac{-9}{11}, \frac{6}{11}, \frac{-2}{11}$

Thus, the direction cosines are $-\frac{9}{11}, \frac{6}{11}$, and $\frac{-2}{11}$.

4. Show that the points $(2,3,4),(-1,-2,1),(5,8,7)$ are collinear.

Solution

The given points are $A(2,3,4), B(-1,-2,1)$, and $C(5,8,7)$.

It is known that the direction ratios of line joining the points, $(x_1, y_1, z_1)$ and $(x_2, y_2, z_2)$, are given by, $x_2-x_1, y_2-y_1$, and $z_2-z_1$.

The direction ratios of $A B$ are $(-1-2),(-2-3)$, and $(1-4)$ i.e., $-3,-5$, and -3 . The direction ratios of $BC$ are $(5-(-1)),(8-(-2))$, and $(7-1)$ i.e., 6,10 , and 6 . It can be seen that the direction ratios of $B C$ are -2 times that of $A B$ i.e., they are proportional.

Therefore, $A B$ is parallel to $B C$. Since point $B$ is common to both $A B$ and $B C$, points $A, B$, and $C$ are collinear.

5. Find the direction cosines of the sides of the triangle whose vertices are $(3,5,-4),(-1,1,2)$ and $(-5,-5,-2)$.

Solution

The vertices of $\triangle A B C$ are $A(3,5,-4), B(-1,1,2)$, and $C(-5,-5,-2)$.

The direction ratios of side $A B$ are $(-1-3),(1-5)$, and $(2-(-4))$ i.e., $-4,-4$, and 6 .

Then, $\sqrt{(-4)^{2}+(-4)^{2}+(6)^{2}}=\sqrt{16+16+36}$

$ \begin{aligned} & =\sqrt{68} \\ & =2 \sqrt{17} \end{aligned} $

Therefore, the direction cosines of $A B$ are

$ \begin{aligned} & \frac{-4}{\sqrt{(-4)^{2}+(-4)^{2}+(6)^{2}}}, \frac{-4}{\sqrt{(-4)^{2}+(-4)^{2}+(6)^{2}}}, \frac{6}{\sqrt{(-4)^{2}+(-4)^{2}+(6)^{2}}} \\ & \frac{-4}{2 \sqrt{17}},-\frac{4}{2 \sqrt{17}}, \frac{6}{2 \sqrt{17}} \\ & \frac{-2}{\sqrt{17}}, \frac{-2}{\sqrt{17}}, \frac{3}{\sqrt{17}} \end{aligned} $

The direction ratios of $BC$ are $(-5-(-1)),(-5-1)$, and $(-2-2)$ i.e., $-4,-6$, and -4 . Therefore, the direction cosines of $B C$ are

$ \begin{aligned} & \frac{-4}{\sqrt{(-4)^{2}+(-6)^{2}+(-4)^{2}}}, \frac{-6}{\sqrt{(-4)^{2}+(-6)^{2}+(-4)^{2}}}, \frac{-4}{\sqrt{(-4)^{2}+(-6)^{2}+(-4)^{2}}} \\ & \text{ i.e., } \frac{-4}{2 \sqrt{17}}, \frac{-6}{2 \sqrt{17}}, \frac{-4}{2 \sqrt{17}} \end{aligned} $

The direction ratios of CA are $(-5-3),(-5-5)$, and $(-2-(-4))$ i.e., $-8,-10$, and 2 . Therefore, the direction cosines of $A C$ are

$ \begin{aligned} & \frac{-8}{\sqrt{(-8)^{2}+(10)^{2}+(2)^{2}}}, \frac{-5}{\sqrt{(-8)^{2}+(10)^{2}+(2)^{2}}}, \frac{2}{\sqrt{(-8)^{2}+(10)^{2}+(2)^{2}}} \\ & \text{ i.e., } \frac{-8}{2 \sqrt{42}}, \frac{-10}{2 \sqrt{42}}, \frac{2}{2 \sqrt{42}} \end{aligned} $

Equation of a Line in Space

We have studied equation of lines in two dimensions in Class XI, we shall now study the vector and cartesian equations of a line in space.

A line is uniquely determined if

(i) it passes through a given point and has given direction, or

(ii) it passes through two given points.

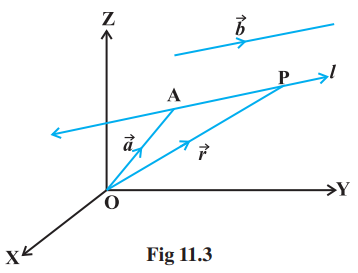
11.3.1 Equation of a line through a given point and parallel to $\vec{a}$ given vector $\vec{b}$ Let $\vec{a}$ be the position vector of the given point A with respect to the origin $O$ of the rectangular coordinate system. Let $l$ be the line which passes through the point $A$ and is parallel to a given vector $\vec{b}$. Let $\vec{r}$ be the position vector of an arbitrary point $P$ on the line (Fig 11.3).

Then $\overrightarrow{{}AP}$ is parallel to the vector $\vec{b}$, i.e., $\overrightarrow{{}AP}=\lambda \vec{b}$, where $\lambda$ is some real number.

But

$$ \overrightarrow{{}AP}=\overrightarrow{{}OP}-\overrightarrow{{}OA} $$

i.e.

$$\lambda \vec{b}=\vec{r}-\vec{a}$$

Conversely, for each value of the parameter $\lambda$, this equation gives the position vector of a point $P$ on the line. Hence, the vector equation of the line is given by

$$ \vec{r}=\vec{a}+\gg \vec{b} $$

Remark If $\vec{b}=a \hat{i}+b \hat{j}+c \hat{k}$, then $a, b, c$ are direction ratios of the line and conversely, if $a, b, c$ are direction ratios of a line, then $\vec{b}=a \hat{i}+b \hat{j}+c \hat{k}$ will be the parallel to the line. Here, $b$ should not be confused with $|\vec{b}|$.

Derivation of cartesian form from vector form

Let the coordinates of the given point $A$ be $(x_1, y_1, z_1)$ and the direction ratios of the line be $a, b, c$. Consider the coordinates of any point $P$ be $(x, y, z)$. Then

$$ \overrightarrow{{}r}=x \hat{i}+y \hat{j}+z \hat{k} ; \overrightarrow{{}a}=x_1 \hat{i}+y_1 \hat{j}+z_1 \hat{k} $$

and

$$ \vec{b}=a \hat{i}+b \hat{j}+c \hat{k} $$

Substituting these values in (1) and equating the coefficients of $\hat{i}, \hat{j}$ and $\hat{k}$, we get

$$ x=x_1+\lambda a ; \quad y=y_1+\lambda b ; z=z_1+\lambda c $$

These are parametric equations of the line. Eliminating the parameter $\lambda$ from (2), we get

$$ \frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c} $$

This is the Cartesian equation of the line.

Note If $l, m, n$ are the direction cosines of the line, the equation of the line is

$$ \frac{x-x_1}{l}=\frac{y-y_1}{m}=\frac{z-z_1}{n} $$

Example 6 Find the vector and the Cartesian equations of the line through the point $(5,2,-4)$ and which is parallel to the vector $3 \hat{i}+2 \hat{j}-8 \hat{k}$.

Solution We have

$$ \vec{a}=5 \hat{i}+2 \hat{j}-4 \hat{k} \text{ and } \vec{b}=3 \hat{i}+2 \hat{j}-8 \hat{k} $$

Therefore, the vector equation of the line is

$$ \vec{r}=5 \hat{i}+2 \hat{j}-4 \hat{k}+\lambda(3 \hat{i}+2 \hat{j}-8 \hat{k}) $$

Now, $\vec{r}$ is the position vector of any point $P(x, y, z)$ on the line.

Therefore, $$\quad x \hat{i}+y \hat{j}+z \hat{k}=5 \hat{i}+2 \hat{j}-4 \hat{k}+\lambda(3 \hat{i}+2 \hat{j}-8 \hat{k})$$

Eliminating $\lambda$, we get

$$ =(5+3 \lambda) \hat{i}+(2+2 \lambda) \hat{j}+(-4-8 \lambda) \hat{k} $$

$$ \frac{x-5}{3}=\frac{y-2}{2}=\frac{z+4}{-8} $$

which is the equation of the line in Cartesian form.

Angle between Two Lines

Let $L_1$ and $L_2$ be two lines passing through the origin and with direction ratios $a_1, b_1, c_1$ and $a_2, b_2, c_2$, respectively. Let $P$ be a point on $L_1$ and $Q$ be a point on $L_2$. Consider the directed lines $OP$ and $OQ$ as given in Fig 11.6. Let $\theta$ be the acute angle between OP and OQ. Now recall that the directed line segments OP and OQ are vectors with components $a_1, b_1, c_1$ and $a_2, b_2, c_2$, respectively. Therefore, the angle $\theta$ between them is given by

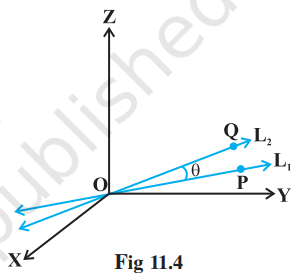
$$ \cos \theta=|\frac{a_1 a_2+b_1 b_2+c_1 c_2}{\sqrt{a_1^{2}+b_1^{2}+c_1^{2}} \sqrt{a_2^{2}+b_2^{2}+c_2^{2}}}| $$

The angle between the lines in terms of $\sin \theta$ is given by

$$ \begin{aligned} \sin \theta & =\sqrt{1-\cos ^{2} \theta} \\ & =\sqrt{1-\frac{(a_1 a_2+b_1 b_2+c_1 c_2)^{2}}{(a_1^{2}+b_1^{2}+c_1^{2})(a_2^{2}+b_2^{2}+c_2^{2})}} \\ & =\frac{\sqrt{(a_1^{2}+b_1^{2}+c_1^{2})(a_2^{2}+b_2^{2}+c_2^{2})-(a_1 a_2+b_1 b_2+c_1 c_2)^{2}}}{\sqrt{(a_1^{2}+b_1^{2}+c_1^{2})} \sqrt{(a_2^{2}+b_2^{2}+c_2^{2})}} \\ & =\frac{\sqrt{(a_1 b_2-a_2 b_1)^{2}+(b_1 c_2-b_2 c_1)^{2}+(c_1 a_2-c_2 a_1)^{2}}}{\sqrt{a_1^{2}+b_1^{2}+c_1^{2}} \sqrt{a_2^{2}+b_2^{2}+c_2^{2}}} \end{aligned} $$

Note In case the lines $L_1$ and $L_2$ do not pass through the origin, we may take lines $L_1^{\prime}$ and $L_2^{\prime}$ which are parallel to $L_1$ and $L_2$ respectively and pass through the origin.

If instead of direction ratios for the lines $L_1$ and $L_2$, direction cosines, namely, $l_1, m_1, n_1$ for $L_1$ and $l_2, m_2, n_2$ for $L_2$ are given, then (1) and (2) takes the following form:

$$ \cos \theta=|l_1 l_2+m_1 m_2+n_1 n_2| \quad(\text{ as } l_1^{2}+m_1^{2}+n_1^{2}=1=l_2^{2}+m_2^{2}+n_2^{2}) $$

and

$$ \sin \theta=\sqrt{(l_1 m_2-l_2 m_1)^{2}-(m_1 n_2-m_2 n_1)^{2}+(n_1 l_2-n_2 l_1)^{2}} $$

Two lines with direction ratios $a_1, b_1, c_1$ and $a_2, b_2, c_2$ are

(i) perpendicular i.e. if $\theta=90^{\circ}$ by (1)

$$ a_1 a_2+b_1 b_2+c_1 c_2=0 $$

(ii) parallel i.e. if $\theta=0$ by (2)

$$ \frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2} $$

Now, we find the angle between two lines when their equations are given. If $\theta$ is acute the angle between the lines

then

$$ \begin{aligned} \vec{r} & =\bar{a}_1+\vec{b}_1 \text { and } \vec{r}=\vec{a}_2+\vec{b}_2 \\ \cos \theta & =\left|\frac{\vec{b}_1 \cdot \vec{b}_2}{\left|\vec{b}_1\right|\left|\vec{b}_2\right|}\right| \end{aligned} $$

In Cartesian form, if $\theta$ is the angle between the lines

$$ \frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1} $$

and

$$ \frac{x-x_2}{a_2}=\frac{y-y_2}{b_2}=\frac{z-z_2}{c_2} $$

where, $a_1, b _{1,} c_1$ and $a _{2,}, b_2, c_2$ are the direction ratios of the lines (1) and (2), respectively, then

$$ \cos \theta=|\frac{a_1 a_2+b_1 b_2+c_1 c_2}{\sqrt{a_1^{2}+b_1^{2}+c_1^{2}} \sqrt{a_2^{2}+b_2^{2}+c_2^{2}}}| $$

Example 7 Find the angle between the pair of lines given by

$$ \vec{r}=3 \hat{i}+2 \hat{j}-4 \hat{k}+\lambda(\hat{i}+2 \hat{j}+2 \hat{k}) $$ and

$$ \vec{r}=5 \hat{i}-2 \hat{j}+\mu(3 \hat{i}+2 \hat{j}+6 \hat{k}) $$

Solution Here $ \vec{b} _ {1}=\hat{i} + 2 \hat{j} + 2 \hat{k} $ and $ \vec{b} _ {2}=3 \hat{i} + 2 \hat{j} + 6 \hat{k} $

The angle $\theta$ between the two lines is given by

$$ \begin{aligned} \cos \theta & = |\frac{ \vec{b} _ {1} \cdot \vec{b} _ {2}}{| \vec{b} _ {1}|| \vec{b} _ {2}|}| = |\frac{(\hat{i} + 2 \hat{j} + 2 \hat{k}) \cdot(3 \hat{i} + 2 \hat{j} + 6 \hat{k})}{\sqrt{1 + 4+ 4} \sqrt{9 + 4 + 36}}| \\ & =|\frac{3+4+12}{3 \times 7}|=\frac{19}{21} \\ \theta & =\cos ^{-1}(\frac{19}{21}) \end{aligned} $$

Hence

Example 8 Find the angle between the pair of lines

and

$$ \begin{aligned} & \frac{x+3}{3}=\frac{y-1}{5}=\frac{z+3}{4} \\ & \frac{x+1}{1}=\frac{y-4}{1}=\frac{z-5}{2} \end{aligned} $$

Solution The direction ratios of the first line are 3, 5, 4 and the direction ratios of the second line are $1,1,2$. If $\theta$ is the angle between them, then

$$ \cos \theta=|\frac{3.1+5.1+4.2}{\sqrt{3^{2}+5^{2}+4^{2}} \sqrt{1^{2}+1^{2}+2^{2}}}|=\frac{16}{\sqrt{50} \sqrt{6}}=\frac{16}{5 \sqrt{2} \sqrt{6}}=\frac{8 \sqrt{3}}{15} $$

Hence, the required angle is $\cos ^{-1}(\frac{8 \sqrt{3}}{15})$.

Shortest Distance between Two Lines

If two lines in space intersect at a point, then the shortest distance between them is zero. Also, if two lines in space are parallel, then the shortest distance between them will be the perpendicular distance, i.e. the length of the perpendicular drawn from a point on one line onto the other line.

Further, in a space, there are lines which are neither intersecting nor parallel. In fact, such pair of lines are non coplanar and are called skew lines. For example, let us consider a room of size 1, 3, 2 units along

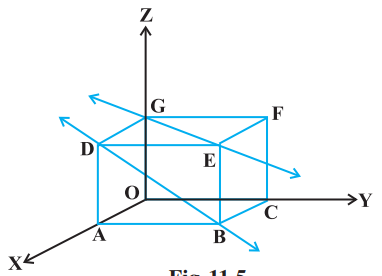
Fig 11.5 $x, y$ and $z$-axes respectively Fig 11.5.

The line GE that goes diagonally across the ceiling and the line DB passes through one corner of the ceiling directly above A and goes diagonally down the wall. These lines are skew because they are not parallel and also never meet.

By the shortest distance between two lines we mean the join of a point in one line with one point on the other line so that the length of the segment so obtained is the smallest.

For skew lines, the line of the shortest distance will be perpendicular to both the lines.

Distance between two skew lines

We now determine the shortest distance between two skew lines in the following way: Let $l_1$ and $l_2$ be two skew lines with equations (Fig. 11.6)

and

$$ \begin{aligned} & \vec{r} = \vec{a} _ {1}+\lambda \vec{b} _ {1} \\ & \vec{r} = \vec{a} _ {2}+\mu \vec{b} _ {2} \end{aligned} $$

Take any point $ S $ on $l_ {1} $ with position vector $ \overrightarrow{{}a}_ {1} $ and $ T $ on $ l_ {2} $, with position vector $ \overrightarrow{{}a}_ {2} $. Then the magnitude of the shortest distance vector will be equal to that of the projection of ST along the direction of the line of shortest distance (See 10.6.2).

If $\overrightarrow{{}PQ}$ is the shortest distance vector between $l_1$ and $l_2$, then it being perpendicular to both $ \vec{b} _1$ and $ \vec{b} _2$, the unit vector $\hat{n}$ along $\overrightarrow{{}PQ}$ would therefore be

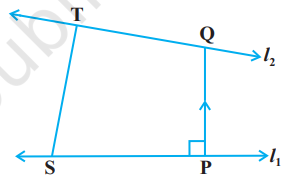
Fig 11.6

$$ \hat{n} = \frac{ \vec{b} _ {1} \times \vec{b} _ {2}}{| \vec{b} _ {1} \times \vec{b} _ {2}|} $$

Then

$$ \overrightarrow{{}PQ}=d \hat{n} $$

where, $d$ is the magnitude of the shortest distance vector. Let $\theta$ be the angle between $\overrightarrow{{}ST}$ and $\overrightarrow{{}PQ}$. Then

But

$$ \begin{aligned} PQ & = ST|\cos \theta| \\ \cos \theta & = |\frac{\overrightarrow{{}PQ} \cdot \overrightarrow{{}ST}}{|\overrightarrow{{}PQ}||\overrightarrow{{}ST}|}| \\ & = |\frac{d \hat{n} \cdot( \vec{a} _ {2}- \vec{a} _ {1})}{d ST}| \quad(\text{ since } \overrightarrow{{}ST}= \vec{a} _ {2}- \vec{a} _ {1}) \\ & = |\frac{( \vec{b} _ {1} \times \vec{b} _ {2}) \cdot( \vec{a} _ {2}- \vec{a} _ {1})}{ST| \vec{b} _ {1} \times \vec{b} _ {2}|}| \end{aligned} $$

Hence, the required shortest distance is

or

$$ \begin{aligned} & d = PQ = ST|\cos \theta| \\ & \boldsymbol{{}d} = |\frac{(\overrightarrow{{}b}_ {1} \times \overrightarrow{{}b}_ {2}) \cdot( \vec{a} _ {2} \times \vec{a} _ {1})}{| \vec{b} _ {1} \times \vec{b} _ {2}|}| \end{aligned} $$

Cartesian form

The shortest distance between the lines

and

$$ \begin{aligned} & l_1: \frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1} \\ & l_2: \frac{x-x_2}{a_2}=\frac{y-y_2}{b_2}=\frac{z-z_2}{c_2} \end{aligned} $$

$$ \left|\frac{ \begin{vmatrix} x_2-x_1 & y_2-y_1 & z_2-z_1 \\ a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \end{vmatrix} }{\sqrt{(b_1 c_2-b_2 c_1)^{2}+(c_1 a_2-c_2 a_1)^{2}+(a_1 b_2-a_2 b_1)^{2}}}\right| $$

Distance between parallel lines

If two lines $l_1$ and $l_2$ are parallel, then they are coplanar. Let the lines be given by

and

$$ \vec{r}= \vec{a} _1+\lambda \vec{b} $$

$$ \vec{r}= \vec{a} _2+\mu \vec{b} $$

where, $ \vec{a} _1$ is the position vector of a point $S$ on $l_1$ and $ \vec{a} _2$ is the position vector of a point $T$ on $l_2$ Fig 11.7.

As $l_1, l_2$ are coplanar, if the foot of the perpendicular from $T$ on the line $l_1$ is $P$, then the distance between the lines $l_1$ and $l_2=|TP|$.

Let $\theta$ be the angle between the vectors $\overrightarrow{{}ST}$ and $\vec{b}$. Then

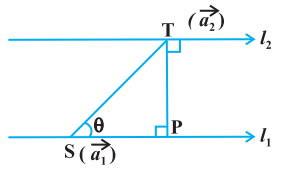
Fig 11.7

$$ \vec{b} \times \overrightarrow{{}ST}=(|\vec{b}||\overrightarrow{{}ST}| \sin \theta) \hat{n} \ldots $$

where $\hat{n}$ is the unit vector perpendicular to the plane of the lines $l_1$ and $l_2$.

But

$$ \overrightarrow{{}ST} = \vec{a} _2 - \vec{a} _1 $$

Therefore, from (3), we get

$$ \begin{matrix} & \quad \vec{b} \times ( \vec{a} _2 - \vec{a} _1) = \vec{b} , |PT| \hat{n} \quad (\text{since } PT = ST \sin \theta) \\ \text{i.e.,} & |\vec{b} \times ( \vec{a} _2 - \vec{a} _1)| = |\vec{b}| , |PT| \cdot 1 \quad (\text{as } |\hat{n}| = 1) \end{matrix} $$

Hence, the distance between the given parallel lines is

$$ d=|\overrightarrow{{}\mathbf{P T}}| = |\frac{\vec{b} \times(\vec{a} _ {2}-\vec{a} _ {1})}{|\vec{b}|}| $$

Example 9 Find the shortest distance between the lines $l_1$ and $l_2$ whose vector equations are

and

$$ \begin{aligned} \vec{r} & =\hat{i}+\hat{j}+\lambda(2 \hat{i}-\hat{j}+\hat{k}) \\ \vec{r} & =2 \hat{i}+\hat{j}-\hat{k}+\mu(3 \hat{i}-5 \hat{j}+2 \hat{k}) \end{aligned} $$

Solution Comparing (1) and (2) with $\vec{r} = \vec{a} _ {1} + \lambda \vec{b} _ {1} $ and $ \overrightarrow{{}r} = \overrightarrow{{}a} _ {2} + \mu \overrightarrow{{}b} _ {2} $ respectively, we get

$$ \vec{r} = \vec{a} _1 + \lambda \vec{b} _1 \quad and \quad \vec{r} = \vec{a} _2 + \mu \vec{b} _2 \mathbf{r} = \mathbf{a} _1 + \lambda \mathbf{b} _1 \quad and \quad \mathbf{r} = \mathbf{a} _2 + \mu \mathbf{b} _2 $$

Therefore

$$ \vec{a} _ {2}-\vec{a} _ {1}=\hat{i}-\hat{k} $$

and

$$ \begin{aligned} \vec{b} _ {1} \times \vec{b} _ {2} & =(2 \hat{i}-\hat{j}+\hat{k}) \times(3 \hat{i}-5 \hat{j}+2 \hat{k}) \\ & = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & -1 & 1 \\ 3 & -5 & 2 \end{vmatrix} =3 \hat{i}-\hat{j}-7 \hat{k} \end{aligned} $$

So

$$ | \vec{b} _ {1} \times \vec{b} _ {2}|=\sqrt{9+1+49}=\sqrt{59} $$

Hence, the shortest distance between the given lines is given by

$$ d=|\frac{(\overrightarrow{{}b}_ {1} \times \overrightarrow{{}b}_ {2}) \cdot(\overrightarrow{{}a}_ {2}-\overrightarrow{{}a}_ {1})}{|\overrightarrow{{}b}_ {1} \times \overrightarrow{{}b}_ {2}|}|=\frac{|3-0+7|}{\sqrt{59}}=\frac{10}{\sqrt{59}} $$

Example 10 Find the distance between the lines $l_1$ and $l_2$ given by

and

$$ \begin{aligned} & \vec{r}=\hat{i}+2 \hat{j}-4 \hat{k}+\lambda(2 \hat{i}+3 \hat{j}+6 \hat{k}) \\ & \vec{r}=3 \hat{i}+3 \hat{j}-5 \hat{k}+\mu(2 \hat{i}+3 \hat{j}+6 \hat{k}) \end{aligned} $$

Solution The two lines are parallel (Why?) We have

$$ \overrightarrow{{}a}_ {1}=\hat{i}+2 \hat{j}-4 \hat{k}, \overrightarrow{{}a}_ {2}=3 \hat{i}+3 \hat{j}-5 \hat{k} \text{ and } \vec{b}=2 \hat{i}+3 \hat{j}+6 \hat{k} $$

Therefore, the distance between the lines is given by

$$ \begin{aligned} & d =\left|\frac{\vec{b} \times( \vec{a} _ {2}- \vec{a} _ {1})}{|\vec{b}|}\right| =\left|\frac{ \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 3 & 6 \\ 2 & 1 & -1 \end{vmatrix} }{\sqrt{4+9+36}}\right| , \\ &=\frac{|-9 \hat{i}+14 \hat{j}-4 \hat{k}|}{\sqrt{49}}=\frac{\sqrt{293}}{\sqrt{49}}=\frac{\sqrt{293}}{7} \\ \end{aligned} $$

EXERCISE 11.2

1. Show that the three lines with direction cosines

$$ \frac{12}{13}, \frac{-3}{13}, \frac{-4}{13} ; \frac{4}{13}, \frac{12}{13}, \frac{3}{13} ; \frac{3}{13}, \frac{-4}{13}, \frac{12}{13} \text{ are mutually perpendicular. } $$

Solution

Two lines with direction cosines, $l_1, m_1, n_1$ and $l_2, m_2, n_2$, are perpendicular to each other, if $l_1 l_2+m_1 m_2+n_1 n_2=0$

(i) For the lines with direction cosines, $\frac{12}{13}, \frac{-3}{13}, \frac{-4}{13}$ and $\frac{4}{13}, \frac{12}{13}, \frac{3}{13}$, we obtain

$ \begin{aligned} l_1 l_2+m_1 m_2+n_1 n_2 & =\frac{12}{13} \times \frac{4}{13}+(\frac{-3}{13}) \times \frac{12}{13}+(\frac{-4}{13}) \times \frac{3}{13} \\ & =\frac{48}{169}-\frac{36}{169}-\frac{12}{169} \\ & =0 \end{aligned} $

Therefore, the lines are perpendicular.

(ii) For the lines with direction cosines, $\frac{4}{13}, \frac{12}{13}, \frac{3}{13}$ and $\frac{3}{13}, \frac{-4}{13}, \frac{12}{13}$, we obtain

$ \begin{aligned} l_1 l_2+m_1 m_2+n_1 n_2 & =\frac{4}{13} \times \frac{3}{13}+\frac{12}{13} \times(\frac{-4}{13})+\frac{3}{13} \times \frac{12}{13} \\ & =\frac{12}{169}-\frac{48}{169}+\frac{36}{169} \\ & =0 \end{aligned} $

Therefore, the lines are perpendicular.

(iii) For the lines with direction cosines, $\frac{3}{13}, \frac{-4}{13}, \frac{12}{13}$ and $\frac{12}{13}, \frac{-3}{13}, \frac{-4}{13}$, we obtain

$ \begin{aligned} l_1 l_2+m_1 m_2+n_1 n_2 & =(\frac{3}{13}) \times(\frac{12}{13})+(\frac{-4}{13}) \times(\frac{-3}{13})+(\frac{12}{13}) \times(\frac{-4}{13}) \\ & =\frac{36}{169}+\frac{12}{169}-\frac{48}{169} \\ & =0 \end{aligned} $

Therefore, the lines are perpendicular.

Thus, all the lines are mutually perpendicular.

2. Show that the line through the points $(1,-1,2),(3,4,-2)$ is perpendicular to the line through the points $(0,3,2)$ and $(3,5,6)$.

Solution

Let $A B$ be the line joining the points, $(1,-1,2)$ and $(3,4,-2)$, and $C D$ be the line joining the points, $(0,3,2)$ and $(3,5,6)$.

The direction ratios, $a_1, b_1, c_1$, of $AB$ are $(3-1),(4-(-1))$, and $(-2-2)$ i.e., 2,5 , and -4 .

The direction ratios, $a_2, b_2, c_2$, of $C D$ are $(3-0),(5-3)$, and $(6-2)$ i.e., 3,2 , and 4.

$A B$ and $C D$ will be perpendicular to each other, if $a_1 a_2+b_1 b_2+c_1 c_2=0$

$a_1 a_2+b_1 b_2+c_1 c_2=2 \times 3+5 \times 2+(-4) \times 4$

$=6+10-16$

$=0$

Therefore, $A B$ and $C D$ are perpendicular to each other.

3. Show that the line through the points $(4,7,8),(2,3,4)$ is parallel to the line through the points $(-1,-2,1),(1,2,5)$.

Solution

Let $A B$ be the line through the points, $(4,7,8)$ and $(2,3,4)$, and $C D$ be the line through the points, $(-1,-2,1)$ and $(1,2,5)$.

The directions ratios, $a_1, b_1, c_1$, of $A B$ are $(2-4),(3-7)$, and $(4-8)$ i.e., $-2,-4$, and -4 .

The direction ratios, $a_2, b_2, c_2$, of $C D$ are $(1-(-1)),(2-(-2))$, and (5 - 1) i.e., 2 , 4 , and 4. $AB$ will be parallel to $CD$, if $\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}$

$\frac{a_1}{a_2}=\frac{-2}{2}=-1$

$\frac{b_1}{b_2}=\frac{-4}{4}=-1$

$\frac{c_1}{c_2}=\frac{-4}{4}=-1$

$\therefore \frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}$

Thus, $A B$ is parallel to $C D$.

4. Find the equation of the line which passes through the point $(1,2,3)$ and is parallel to the vector $3 \hat{i}+2 \hat{j}-2 \hat{k}$.

Solution

It is given that the line passes through the point $A(1,2,3)$. Therefore, the position vector through A is $\vec{a}=\hat{i}+2 \hat{j}+3 \hat{k}$

$\vec{b}=3 \hat{i}+2 \hat{j}-2 \hat{k}$

It is known that the line which passes through point A and parallel to $\vec{b}$ is given by

$\vec{r}=\vec{a}+\lambda \vec{b}$, where $\lambda$ is a constant.

$\Rightarrow \vec{r}=\hat{i}+2 \hat{j}+3 \hat{k}+\lambda(3 \hat{i}+2 \hat{j}-2 \hat{k})$

This is the required equation of the line.

5. Find the equation of the line in vector and in cartesian form that passes through the point with position vector $2 \hat{i}-j+4 \hat{k}$ and is in the direction $\hat{i}+2 \hat{j}-\hat{k}$.

Solution

It is given that the line passes through the point with position vector $\vec{a}=2 \hat{i}-\hat{j}+4 \hat{k}$

$\vec{b}=\hat{i}+2 \hat{j}-\hat{k}$

It is known that a line through a point with position vector $\vec{a}$ and parallel to $\vec{b}$ is given by the equation, $\vec{r}=\vec{a}+\lambda \vec{b}$

$\Rightarrow \vec{r}=2 \hat{i}-\hat{j}+4 \hat{k}+\lambda(\hat{i}+2 \hat{j}-\hat{k})$

This is the required equation of the line in vector form.

$\vec{r}=x \hat{i}-y \hat{j}+z \hat{k}$

$\Rightarrow x \hat{i}-y \hat{j}+z \hat{k}=(\lambda+2) \hat{i}+(2 \lambda-1) \hat{j}+(-\lambda+4) \hat{k}$

Eliminating $\lambda$, we obtain the Cartesian form equation as

$\frac{x-2}{1}=\frac{y+1}{2}=\frac{z-4}{-1}$

This is the required equation of the given line in Cartesian form.

6. Find the cartesian equation of the line which passes through the point $(-2,4,-5)$ and parallel to the line given by $\frac{x+3}{3}=\frac{y-4}{5}=\frac{z+8}{6}$.

Solution

It is given that the line passes through the point $(-2,4,-5)$ and is parallel to $\frac{x+3}{3}=\frac{y-4}{5}=\frac{z+8}{6}$

The direction ratios of the line, $\frac{x+3}{3}=\frac{y-4}{5}=\frac{z+8}{6}$, are 3,5 , and 6 .

The required line is parallel to $\frac{x+3}{3}=\frac{y-4}{5}=\frac{z+8}{6}$

Therefore, its direction ratios are $3 k, 5 k$, and $6 k$, where $k \neq 0$

It is known that the equation of the line through the point $(x_1, y_1, z_1)$ and with direction

ratios, $a, b, c$, is given by $\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}$

Therefore the equation of the required line is

$\frac{x+2}{3 k}=\frac{y-4}{5 k}=\frac{z+5}{6 k}$

$\Rightarrow \frac{x+2}{3}=\frac{y-4}{5}=\frac{z+5}{6}=k$

7. The cartesian equation of a line is $\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{2}$. Write its vector form.

Solution

The Cartesian equation of the line is

$\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{2}$

The given line passes through the point $(5,-4,6)$. The position vector of this point is

$\vec{a}=5 \hat{i}-4 \hat{j}+6 \hat{k}$

Also, the direction ratios of the given line are 3,7 , and 2 .

This means that the line is in the direction of vector, $\vec{b}=3 \hat{i}+7 \hat{j}+2 \hat{k}$

It is known that the line through position vector $\vec{a}$ and in the direction of the $\vec{b}$ is given by the equation, $\vec{r}=\vec{a}+\lambda \vec{b}, \lambda \in R$

$\Rightarrow \vec{r}=(5 \hat{i}-4 \hat{j}+6 \hat{k})+\lambda(3 \hat{i}+7 \hat{j}+2 \hat{k})$

This is the required equation of the given line in vector form.

8. Find the angle between the following pairs of lines:

$\quad\quad$(i) $\vec{r}=2 \hat{i}-5 \hat{j}+\hat{k}+\lambda(3 \hat{i}+2 \hat{j}+6 \hat{k})$ and

$\quad\quad$ $ \vec{r}=7 \hat{i}-6 \hat{k}+\mu(\hat{i}+2 \hat{j}+2 \hat{k}) $

$\quad\quad$(ii) $\vec{r}=3 \hat{i}+\hat{j}-2 \hat{k}+\lambda(\hat{i}-\hat{j}-2 \hat{k})$ and

$\quad\quad$ $ \vec{r}=2 \hat{i}-\hat{j}-56 \hat{k}+\mu(3 \hat{i}-5 \hat{j}-4 \hat{k}) $

Solution

(i) Let $Q$ be the angle between the given lines.

The angle between the given pairs of lines is given by, $\cos Q=|\frac{ \vec{b} _1 \cdot \vec{b} _2}{| \vec{b} _1|| \vec{b} _2|}|$

The given lines are parallel to the vectors, $ \vec{b} _1=3 \hat{i}+2 \hat{j}+6 \hat{k}$ and $ \vec{b} _2=\hat{i}+2 \hat{j}+2 \hat{k}$, respectively.

$ \begin{aligned} \therefore| \vec{b} _1| & =\sqrt{3^{2}+2^{2}+6^{2}}=7 \\ | \vec{b} _2| & =\sqrt{(1)^{2}+(2)^{2}+(2)^{2}}=3 \\ \vec{b} _1 \cdot \vec{b} _2 & =(3 \hat{i}+2 \hat{j}+6 \hat{k}) \cdot(\hat{i}+2 \hat{j}+2 \hat{k}) \\ & =3 \times 1+2 \times 2+6 \times 2 \\ & =3+4+12 \\ & =19 \end{aligned} $

$\Rightarrow \cos Q=\frac{19}{7 \times 3}$

$\Rightarrow Q=\cos ^{-1}(\frac{19}{21})$

(ii) The given lines are parallel to the vectors, $ \vec{b} _1=\hat{i}-\hat{j}-2 \hat{k}$ and $ \vec{b} _2=3 \hat{i}-5 \hat{j}-4 \hat{k}$, respectively.

$ \begin{aligned} & \therefore| \vec{b} _1|=\sqrt{(1)^{2}+(-1)^{2}+(-2)^{2}}=\sqrt{6} \\ & | \vec{b} _2|=\sqrt{(3)^{2}+(-5)^{2}+(-4)^{2}}=\sqrt{50}=5 \sqrt{2} \\ & \vec{b} _1 \cdot \vec{b} _2=(\hat{i}-\hat{j}-2 \hat{k}) \cdot(3 \hat{i}-5 \hat{j}-4 \hat{k}) \\ & =1 \cdot 3-1(-5)-2(-4) \\ & =3+5+8 \\ & =16 \\ & \cos Q=|\frac{ \vec{b} _1 \cdot \vec{b} _2}{| \vec{b} _1|| \vec{b} _2|}| \\ & \Rightarrow \cos Q=\frac{16}{\sqrt{6} \cdot 5 \sqrt{2}}=\frac{16}{\sqrt{2} \cdot \sqrt{3} \cdot 5 \sqrt{2}}=\frac{16}{10 \sqrt{3}} \\ & \Rightarrow \cos Q=\frac{8}{5 \sqrt{3}} \\ & \Rightarrow Q=\cos ^{-1}(\frac{8}{5 \sqrt{3}}) \end{aligned} $

9. Find the angle between the following pair of lines:

$\quad\quad$(i) $\frac{x-2}{2}=\frac{y-1}{5}=\frac{z+3}{-3}$ and $\frac{x+2}{-1}=\frac{y-4}{8}=\frac{z-5}{4}$

$\quad\quad$(ii) $\frac{x}{2}=\frac{y}{2}=\frac{z}{1}$ and $\frac{x-5}{4}=\frac{y-2}{1}=\frac{z-3}{8}$

Solution

Let $ \vec{b} _1$ and $ \vec{b} _2$ be the vectors parallel to the pair of lines,

$ \begin{aligned} & \frac{x-2}{2}=\frac{y-1}{5}=\frac{z+3}{-3} \text{ and } \frac{x+2}{-1}=\frac{y-4}{8}=\frac{z-5}{4} \text{, respectively. } \\ & \therefore \vec{b} _1=2 \hat{i}+5 \hat{j}-3 \hat{k} \text{ and } \vec{b} _2=-\hat{i}+8 \hat{j}+4 \hat{k} \\ & | \vec{b} _1|=\sqrt{(2)^{2}+(5)^{2}+(-3)^{2}}=\sqrt{38} \\ & | \vec{b} _2|=\sqrt{(-1)^{2}+(8)^{2}+(4)^{2}}=\sqrt{81}=9 \\ & \vec{b} _1 \cdot \vec{b} _2=(2 \hat{i}+5 \hat{j}-3 \hat{k}) \cdot(-\hat{i}+8 \hat{j}+4 \hat{k}) \\ & =2(-1)+5 \times 8+(-3) \cdot 4 \\ & =-2+40-12 \\ & =26 \end{aligned} $

The angle, $Q$, between the given pair of lines is given by the relation,

$ \begin{aligned} & \cos Q=|\frac{ \vec{b} _1 \cdot \vec{b} _2}{| \vec{b} _1|| \vec{b} _2|}| \\ & \Rightarrow \cos Q=\frac{26}{9 \sqrt{38}} \\ & \Rightarrow Q=\cos ^{-1}(\frac{26}{9 \sqrt{38}}) \end{aligned} $

(ii) Let $ \vec{b} _1, \vec{b} _2$ be the vectors parallel to the given pair of lines, $\frac{x}{2}=\frac{y}{2}=\frac{z}{1}$ and $\frac{x-5}{4}=\frac{y-5}{1}=\frac{z-3}{8}$, respectively.

$ \begin{aligned} & \vec{b} _1=2 \hat{i}+2 \hat{j}+\hat{k} \\ & \vec{b} _2=4 \hat{i}+\hat{j}+8 \hat{k} \\ & \therefore| \vec{b} _1|=\sqrt{(2)^{2}+(2)^{2}+(1)^{2}}=\sqrt{9}=3 \\ & | \vec{b} _2|=\sqrt{4^{2}+1^{2}+8^{2}}=\sqrt{81}=9 \\ & \vec{b} _1 \cdot \vec{b} _2=(2 \hat{i}+2 \hat{j}+\hat{k}) \cdot(4 \hat{i}+\hat{j}+8 \hat{k}) \\ & \quad=2 \times 4+2 \times 1+1 \times 8 \\ & \quad=8+2+8 \\ & \quad=18 \end{aligned} $

If $Q$ is the angle between the given pair of lines, then $\cos Q=|\frac{ \vec{b} _1 \cdot \vec{b} _2}{| \vec{b} _1|| \vec{b} _2|}|$

$\Rightarrow \cos Q=\frac{18}{3 \times 9}=\frac{2}{3}$

$\Rightarrow Q=\cos ^{-1}(\frac{2}{3})$

10. Find the values of $p$ so that the lines $\frac{1-x}{3}=\frac{7 y-14}{2 p}=\frac{z-3}{2}$ and $\frac{7-7 x}{3 p}=\frac{y-5}{1}=\frac{6-z}{5}$ are at right angles.

Solution

The given equations can be written in the standard form as

$ \frac{x-1}{-3}=\frac{y-2}{\frac{2 p}{7}}=\frac{z-3}{2} \text{ and } \frac{x-1}{\frac{-3 p}{7}}=\frac{y-5}{1}=\frac{z-6}{-5} $

The direction ratios of the lines are $-3, \frac{2 p}{7}, 2$ and $\frac{-3 p}{7}, 1,-5$ respectively.

Two lines with direction ratios, $a_1, b_1, c_1$ and $a_2, b_2, c_2$, are perpendicular to each other, if $a_1 a_2+b_1 b_2+c_1 c_2=0$ $\therefore(-3) \cdot(\frac{-3 p}{7})+(\frac{2 p}{7}) \cdot(1)+2 \cdot(-5)=0$

$\Rightarrow \frac{9 p}{7}+\frac{2 p}{7}=10$

$\Rightarrow 11 p=70$

$\Rightarrow p=\frac{70}{11}$

Thus, the value of $p$ is $\frac{70}{11}$.

11. Show that the lines $\frac{x-5}{7}=\frac{y+2}{-5}=\frac{z}{1}$ and $\frac{x}{1}=\frac{y}{2}=\frac{z}{3}$ are perpendicular to each other.

Solution

The equations of the given lines are $\frac{x-5}{7}=\frac{y+2}{-5}=\frac{z}{1}$ and $\frac{x}{1}=\frac{y}{2}=\frac{z}{3}$

The direction ratios of the given lines are $7,-5,1$ and $1,2,3$ respectively.

Two lines with direction ratios, $a_1, b_1, c_1$ and $a_2, b_2, c_2$, are perpendicular to each other, if $a_1 a_2+b_1 b_2+c_1 c_2=0$

$\therefore 7 \times 1+(-5) \times 2+1 \times 3$

$=7-10+3$

$=0$

Therefore, the given lines are perpendicular to each other.

12. Find the shortest distance between the lines

$\quad\quad$ $ \begin{aligned} & \vec{r}=(\hat{i}+2 \hat{j}+\hat{k})+\lambda(\hat{i}-\hat{j}+\hat{k}) \text{ and } \\ & \vec{r}=2 \hat{i}-\hat{j}-\hat{k}+\mu(2 \hat{i}+\hat{j}+2 \hat{k}) \end{aligned} $

Solution

The equations of the given lines are

$\vec{r}=(\hat{i}+2 \hat{j}+\hat{k})+\lambda(\hat{i}-\hat{j}+\hat{k})$

$\vec{r}=2 \hat{i}-\hat{j}-\hat{k}+\mu(2 \hat{i}+\hat{j}+2 \hat{k})$

It is known that the shortest distance between the lines, $\vec{r}= \vec{a} _1+\lambda \vec{b} _1$ and $\vec{r}= \vec{a} _2+\mu \vec{b} _2$, is given by,

$d=|\frac{( \vec{b} _1 \times \vec{b} _2) \cdot( \vec{a} _2- \vec{a} _2)}{|\overrightarrow{{}b_1} \times \vec{b} _2|}|$

Comparing the given equations, we obtain

$ \begin{aligned} & \vec{a} _1=\hat{i}+2 \hat{j}+\hat{k} \\ & \vec{b} _1=\hat{i}-\hat{j}+\hat{k} \\ & \vec{a} _2=2 \hat{i}-\hat{j}-\hat{k} \\ & \vec{b} _2=2 \hat{i}+\hat{j}+2 \hat{k} \\ & \vec{a} _2- \vec{a} _1=(2 \hat{i}-\hat{j}-\hat{k})-(\hat{i}+2 \hat{j}+\hat{k})=\hat{i}-3 \hat{j}-2 \hat{k} \\ & \vec{b} _1 \times \vec{b} _2= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & -1 & 1 \\ 2 & 1 & 2 \end{vmatrix} \\ & \vec{b} _1 \times \vec{b} _2=(-2-1) \hat{i}-(2-2) \hat{j}+(1+2) \hat{k}=-3 \hat{i}+3 \hat{k} \\ & \Rightarrow| \vec{b} _1 \times \vec{b} _2|=\sqrt{(-3)^{2}+(3)^{2}}=\sqrt{9+9}=\sqrt{18}=3 \sqrt{2} \end{aligned} $

Substituting all the values in equation (1), we obtain

$ \begin{aligned} & d=|\frac{(-3 \hat{i}+3 \hat{k}) \cdot(\hat{i}-3 \hat{j}-2 \hat{k})}{3 \sqrt{2}}| \\ & \Rightarrow d=|\frac{-3.1+3(-2)}{3 \sqrt{2}}| \\ & \Rightarrow d=|\frac{-9}{3 \sqrt{2}}| \\ & \Rightarrow d=\frac{3}{\sqrt{2}}=\frac{3 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}}=\frac{3 \sqrt{2}}{2} \end{aligned} $

Therefore, the shortest distance between the two lines is $\frac{3 \sqrt{2}}{2}$ units.

13. Find the shortest distance between the lines

$\quad\quad$ $\frac{x+1}{7}=\frac{y+1}{-6}=\frac{z+1}{1}$ and $\frac{x-3}{1}=\frac{y-5}{-2}=\frac{z-7}{1}$

Solution

The given lines are $\frac{x+1}{7}=\frac{y+1}{-6}=\frac{z+1}{1}$ and $\frac{x-3}{1}=\frac{y-5}{-2}=\frac{z-7}{1}$

It is known that the shortest distance between the two lines,

$\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1}$ and $\frac{x-x_2}{a_2}=\frac{y-y_2}{b_2}=\frac{z-z_2}{c_2}$, is given by,

$d=\frac{ \begin{vmatrix} x_2-x_1 & y_2-y_1 & z_2-z_1 \\ a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2\end{vmatrix} }{\sqrt{(b_1 c_2-b_2 c_1)^{2}+(c_1 a_2-c_2 a_1)^{2}+(a_1 b_2-a_2 b_1)^{2}}}$

Comparing the given equations, we obtain

$ \begin{aligned} & x_1=-1, y_1=-1, z_1=-1 \\ & a_1=7, \quad b_1=-6, c_1=1 \\ & x_2=3, \quad y_2=5, z_2=7 \\ & a_2=1, \quad b_2=-2, c_2=1 \\ & \text{ Then, } \begin{vmatrix} x_2-x_1 & y_2-y_1 & z_2-z_1 \\ a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \end{vmatrix} = \begin{vmatrix} 4 & 6 & 8 \\ 7 & -6 & 1 \\ 1 & -2 & 1 \end{vmatrix} \\ & =4(-6+2)-6(7-1)+8(-14+6) \\ & =-16-36-64 \\ & =-116 \\ & \Rightarrow \sqrt{(b_1 c_2-b_2 c_1)^{2}+(c_1 a_2-c_2 a_1)^{2}+(a_1 b_2-a_2 b_1)^{2}}=\sqrt{(-6+2)^{2}+(1+7)^{2}+(-14+6)^{2}} \\ & =\sqrt{16+36+64} \\ & =\sqrt{116} \\ & =2 \sqrt{29} \end{aligned} $

Substituting all the values in equation (1), we obtain

$d=\frac{-116}{2 \sqrt{29}}=\frac{-58}{\sqrt{29}}=\frac{-2 \times 29}{\sqrt{29}}=-2 \sqrt{29}$

Since distance is always non-negative, the distance between the given lines is $2 \sqrt{29}$ units.

14. Find the shortest distance between the lines whose vector equations are $\vec{r}=(\hat{i}+2 \hat{j}+3 \hat{k})+\lambda(\hat{i}-3 \hat{j}+2 \hat{k})$ and $\vec{r}=4 \hat{i}+5 \hat{j}+6 \hat{k}+\mu(2 \hat{i}+3 \hat{j}+\hat{k})$

Solution

The given lines are $\vec{r}=\hat{i}+2 \hat{j}+3 \hat{k}+\lambda(\hat{i}-3 \hat{j}+2 \hat{k})$ and $\vec{r}=4 \hat{i}+5 \hat{j}+6 \hat{k}+\mu(2 \hat{i}+3 \hat{j}+\hat{k})$

It is known that the shortest distance between the lines, $\vec{r}= \vec{a} _1+\lambda \vec{b} _1$ and $\vec{r}= \vec{a} _2+\mu \vec{b} _2$, is given by, $d=|\frac{( \vec{b} _1 \times \vec{b} _2) \cdot( \vec{a} _2- \vec{a} _2)}{| \vec{b} _1 \times \vec{b} _2|}|$

Comparing the given equations with $\vec{r}= \vec{a} _1+\lambda \vec{b} _1$ and $\vec{r}= \vec{a} _2+\mu \vec{b} _2$, we obtain

$ \begin{aligned} & \vec{a} _1=\hat{i}+2 \hat{j}+3 \hat{k} \\ & \vec{b} _1=\hat{i}-3 \hat{j}+2 \hat{k} \\ & \vec{a} _2=4 \hat{i}+5 \hat{j}+6 \hat{k} \\ & \vec{b} _2=2 \hat{i}+3 \hat{j}+\hat{k} \\ & \vec{a} _2- \vec{a} _1=(4 \hat{i}+5 \hat{j}+6 \hat{k})-(\hat{i}+2 \hat{j}+3 \hat{k})=3 \hat{i}+3 \hat{j}+3 \hat{k} \\ & \vec{b} _1 \times \vec{b} _2= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & -3 & 2 \\ 2 & 3 & 1 \end{vmatrix} =(-3-6) \hat{i}-(1-4) \hat{j}+(3+6) \hat{k}=-9 \hat{i}+3 \hat{j}+9 \hat{k} \\ & \Rightarrow| \vec{b} _1 \times \vec{b} _2|=\sqrt{(-9)^{2}+(3)^{2}+(9)^{2}}=\sqrt{81+9+81}=\sqrt{171}=3 \sqrt{19} \\ & ( \vec{b} _1 \times \vec{b} _2) \cdot( \vec{a} _2- \vec{a} _1)=(-9 \hat{i}+3 \hat{j}+9 \hat{k}) \cdot(3 \hat{i}+3 \hat{j}+3 \hat{k}) \\ & =-9 \times 3+3 \times 3+9 \times 3 \\ & =9 \end{aligned} $

Substituting all the values in equation (1), we obtain

$d=|\frac{9}{3 \sqrt{19}}|=\frac{3}{\sqrt{19}}$

Therefore, the shortest distance between the two given lines is $\frac{3}{\sqrt{19}}$ units.

15. Find the shortest distance between the lines whose vector equations are $\vec{r}=(1-t) \hat{i}+(t-2) \hat{j}+(3-2 t) \hat{k}$ and $\vec{r}=(s+1) \hat{i}+(2 s-1) \hat{j}-(2 s+1) \hat{k}$

Solution

The given lines are $\vec{r}=(1-t) \hat{i}+(t-2) \hat{j}+(3-2 t) \hat{k}$

$\Rightarrow \vec{r}=(\hat{i}-2 \hat{j}+3 \hat{k})+t(-\hat{i}+\hat{j}-2 \hat{k})$

$\vec{r}=(s+1) \hat{i}+(2 s-1) \hat{j}-(2 s+1) \hat{k}$

$\Rightarrow \vec{r}=(\hat{i}-\hat{j}+\hat{k})+s(\hat{i}+2 \hat{j}-2 \hat{k})$

It is known that the shortest distance between the lines, $\vec{r}= \vec{a} _1+\lambda \vec{b} _1$ and $\vec{r}= \vec{a} _2+\mu \vec{b} _2$, is given by,

$d=|\frac{( \vec{b} _1 \times \vec{b} _2) \cdot( \vec{a} _2- \vec{a} _2)}{| \vec{b} _1 \times \vec{b} _2|}|$

For the given equations,

$ \vec{a} _1=\hat{i}-2 \hat{j}+3 \hat{k}$

$ \vec{b} _1=-\hat{i}+\hat{j}-2 \hat{k}$

$ \vec{a} _2=\hat{i}-\hat{j}-\hat{k}$

$ \vec{b} _2=\hat{i}+2 \hat{j}-2 \hat{k}$

$ \vec{a} _2- \vec{a} _1=(\hat{i}-\hat{j}-\hat{k})-(\hat{i}-2 \hat{j}+3 \hat{k})=\hat{j}-4 \hat{k}$

$ \vec{b} _1 \times \vec{b} _2= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ -1 & 1 & -2 \\ 1 & 2 & -2\end{vmatrix} =(-2+4) \hat{i}-(2+2) \hat{j}+(-2-1) \hat{k}=2 \hat{i}-4 \hat{j}-3 \hat{k}$

$\Rightarrow| \vec{b} _1 \times \vec{b} _2|=\sqrt{(2)^{2}+(-4)^{2}+(-3)^{2}}=\sqrt{4+16+9}=\sqrt{29}$

$\therefore( \vec{b} _1 \times \vec{b} _2) \cdot( \vec{a} _2- \vec{a} _1)=(2 \hat{i}-4 \hat{j}-3 \hat{k}) \cdot(\hat{j}-4 \hat{k})=-4+12=8$

Substituting all the values in equation (3), we obtain

$d=|\frac{8}{\sqrt{29}}|=\frac{8}{\sqrt{29}}$

Therefore, the shortest distance between the lines is $\frac{8}{\sqrt{29}}$ units.

11.6 Plane

A plane is determined uniquely if any one of thefollowing is known:

(i) thenormal to the plane and itsdist ance from the origin is given, i.e., equation of a plane in normal form.

(ii) it passes through a point and is perpendicular to a given direction.

(iii) it passes through three given non collinear points.

Now we shall find vector and Cartesian equations of the planes.

11.6.1 Equation of a plane in normal form

Consider a plane whose perpendicular distance from theorigin is $d(d \neq 0)$. Fig 11.10

If $\overrightarrow{\mathrm{ON}}$ isthe normal from the origin to the plane, and $\overline{k^{\circ}}$ is the unit normal vector along $\overrightarrow{\mathrm{ON}}$. Then $\overrightarrow{\mathrm{ON}}=d \stackrel{\check{w}}{ }$. Let $\mathrm{P}$ be any point on the plane. Therefore, $\overrightarrow{\mathrm{NP}}$ is perpendicular to $\overrightarrow{\mathrm{ON}}$.

Therefore, $\overrightarrow{\mathrm{NP}} \cdot \overrightarrow{\mathrm{ON}}=0$

Let $\vec{r}$ betheposition vect or of the point $\mathrm{P}$, then $\overrightarrow{\mathrm{NP}}=\vec{r}-d \stackrel{\leftarrow}{4}$ (as $\overrightarrow{\mathrm{ON}}+\overrightarrow{\mathrm{NP}} \overrightarrow{\mathrm{OP}_{\mathrm{P}}}$ ) Therefore, (1) becomes

$$ (\vec{r}-d \hat{n}) \cdot d \hat{n}=0 $$

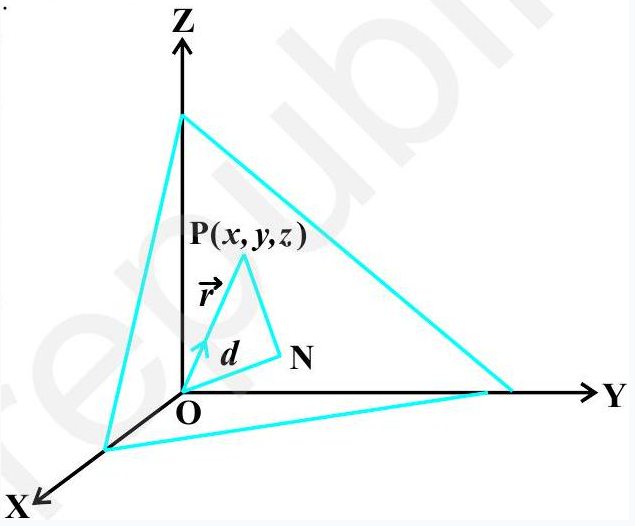
Fig 11.10

or

$$ (\vec{r}-d \hat{n}) \cdot \hat{n}=0 \quad(d \neq 0) $$

or

$$ \vec{r} \cdot \hat{n}-d \hat{n} \cdot \hat{n}=0 $$

$$ \begin{array}{ll} \text { i.e., } \quad \overrightarrow{\boldsymbol{r}} \cdot \hat{\boldsymbol{n}}=\boldsymbol{d} \quad(\text { as } \hat{n} \cdot \hat{n}=1) \tag{2} \end{array} $$

This is the vector form of the equation of the plane.

Cartesian form

Equation(2) gives the vector equation of a plane, where $\bar{k}$ is the unit vector normal to the plane. Let $\mathrm{P}(x, y, z)$ beany point on the plane. Then

$$ \overrightarrow{\mathrm{OP}}=x \hat{i}+y \hat{j}, z \hat{k} $$

Let $l, m, n$ be the direction cosines of $\hat{n}$. Then

$$ \hat{n}=l \hat{i}+m \hat{j}+n \hat{k} $$

Therefore, (2) gives

i.e.,

$$ (x \hat{i}+y \hat{j}, z \hat{k}).(l \hat{i}+m \hat{j}+n \hat{k})=d $$

$$ \begin{aligned} & l x+m y+n z=d \end{aligned} $$

This is the cartesian equation of the plane in the normal form.

- Note Equation (3) shows that if $r.(a \hat{i}+b \hat{j}+c \hat{k})$ isthe vect or equation of a plane, then $a x+b y+c z=d$ is the Cartesian equation of the plane, where $a, b$ and $c$ are the direction ratiosof the normal to the plane.

Example 13 Find the vector equation of the plane which is at a distance of $\frac{6}{\sqrt{29}}$ from the origin anditsnormal vector from the origin is $a\hat{i}-3 \hat{j}+4 \hat{k}$

Solution Let $ \hat{n}=2 \hat{i}-3 \hat{j}+4 \hat{k} $ Then

$$ \hat{n}=\frac{\vec{n}}{|\vec{n}|}=\frac{2 \hat{i}-3 \hat{j}+4 \hat{k}}{\sqrt{4+9+16}}=\frac{2 \hat{i}-3 \hat{j}+4 \hat{k}}{\sqrt{29}} $$

Hence, the required equation of the plane is

$$ \vec{r} \cdot\left(\frac{2}{\sqrt{29}} \hat{i}+\frac{-3}{\sqrt{29}} \hat{j}+\frac{4}{\sqrt{29}} \hat{k}\right)=\frac{6}{\sqrt{29}} $$

Example 14 Find thedirection cosines of the unit vector perpendicular to the plane

$$ r.(6 \hat{i}-3 \hat{j}-2 \hat{k})+1=0 $$ passing through the origin.

Solution The given equation can be written as

$$ r.(-6 \hat{i}+3 \hat{j}+2 \hat{k})=1 $$

Now $$ \left|-6 \hat{i}+3 \hat{j}+2 \hat{k}\right|=\sqrt{36+4+7}=7 $$

Therefore, dividing both sides of (1) by 7 , we get

$$ \vec{r} \cdot\left(-\frac{6}{7} \hat{i}_{+} \frac{3}{7} \hat{j}+\frac{2}{7} \hat{k}\right)=\frac{1}{7} $$

which is theequation of the plane in the form $\vec{r} \cdot \hat{n}=d$.

This shows that

$$ \hat{n}=-\frac{6}{7} \hat{i} + \frac{3}{7} \hat{j}+\frac{2}{7} \hat{k} $$ a unit vector perpendicular to the

plane through the origin. Hence, the direction cosines of $\large \hat{n}$ are $\frac{-6}{7}, \frac{3}{7}, \frac{2}{7}$

Example 15 Find the distance of the plane 2 x - 3 y+4 z - 6=0 from theorigin.

Solution Since the direction ratios of the normal to the plane are $2, - 3,4$; the direction cosinesof it are

$$ \frac{2}{\sqrt{2^{2}+(-3)^{2}+4^{2}}}, \frac{-3}{\sqrt{2^{2}+(-3)^{2}+4^{2}}}, \frac{4}{\sqrt{2^{2}+(-3)^{2}+4^{2}}} \text {, i.e., } \frac{2}{\sqrt{29}}, \frac{-3}{\sqrt{29}}, \frac{4}{\sqrt{29}} $$

Hence, dividing the equation 2 x -3 y+4 z- 6=0 i.e., 2 x -3 y+4 z=6 throughout by $\sqrt{29}$, we get

$$ \frac{2}{\sqrt{29}} x+\frac{-3}{\sqrt{29}} y+\frac{4}{\sqrt{29}} z=\frac{6}{\sqrt{29}} $$

This is of the form l x+m y+n z=d, where $d$ is the distance of the plane from the origin. So, the distance of the plane from theorigin is $\frac{6}{\sqrt{29}}$.

Example 16 Find the coordinates of the foot of the perpendicular drawn from the origin to the plane 2x+3y+4z-6=0.

Solution Let thecoordinates of the foot of the perpendicular $\mathrm{P}$ from the origin to the planeis $\left(x_{1}, y_{1}, z_{1}\right)$ (Fig11.11).

Then, the direction ratios of the line OP are $x_{1}, y_{1}, z_{1}$.

Writingthe equation of the plane in the normal form, we have

$$ \frac{2}{\sqrt{29}} x-\frac{3}{\sqrt{29}} y+\frac{4}{\sqrt{29}} z=\frac{6}{\sqrt{29}} $$

where, $\frac{2}{\sqrt{29}}, \frac{-3}{\sqrt{29}}, \frac{4}{\sqrt{29}}$ are the direction cosines of the OP.

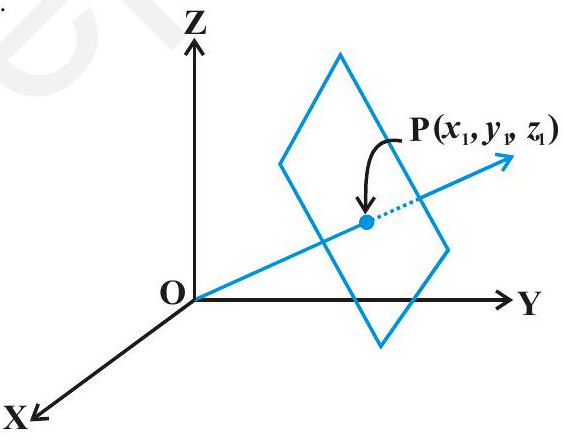
Fig 11.11

Since $d . c$.’s and direction ratios of a line are proportional, we have

i.e.,

$$ \begin{aligned} \frac{x_{1}}{\frac{2}{\sqrt{29}}} & =\frac{y_{1}}{\frac{-3}{\sqrt{29}}}=\frac{z_{1}}{\frac{4}{\sqrt{29}}}=k \ x_{1} & =\frac{2 k}{\sqrt{29}}, y_{1}=\frac{-3 k}{\sqrt{29}}, z_{1}=\frac{4 k}{\sqrt{29}} \end{aligned} $$

Substituting these in the equation of the plane, we get $k=\frac{6}{\sqrt{29}}$.

Hence, the foot of the perpendicular is $\left(\frac{12}{29}, \frac{-18}{29}, \frac{24}{29}\right)$.

Note If $d$ is the distance from the origin and $l, m, n$ are the direction cosines of the normal to the plane through the origin, then the foot of the perpendicular is $(l d, m d, n d)$.

11.6.2 Equation of a plane perpendicular to a given vector and passing through a given point In the space, there can be many planes that are perpendicular to the given vector, but through a given point $\mathbf{P}\left(x_{1}, y_{1}, z_{1}\right.)$ , only one such plane exists (see Fig 11.12).

Let a plane pass through a point A with position vector $\vec{a}$ and perpendicularto the vector $\vec{N}$.

Let $\vec{r}$ bethe position vector of any point $\mathrm{P}(x, y, z)$ in the plane.(Fig11.13).

Then the point $\mathrm{P}$ lies in the plane if and only if $\overrightarrow{\mathrm{AP}}$ is perpendicular to $\overrightarrow{\mathrm{N}}$. i.e., $\overrightarrow{\mathrm{AP}} \cdot \overrightarrow{\mathrm{N}}=0$. But $\overrightarrow{\mathrm{AP}}=\vec{r}-\vec{a}$. Therefore, $(\overrightarrow{\boldsymbol{r}}-\overrightarrow{\boldsymbol{a}}) \cdot \overrightarrow{\mathbf{N}}=\mathbf{0}$

This is the vector equation of the plane.

Cartesian form

Let the given point Abe $\left(x_{1}, y_{1}, z_{1}\right), \mathrm{P}$ be $(x, y, z)$ and direction ratios of $\overrightarrow{\mathrm{N}}$ are A, B and C. Then,

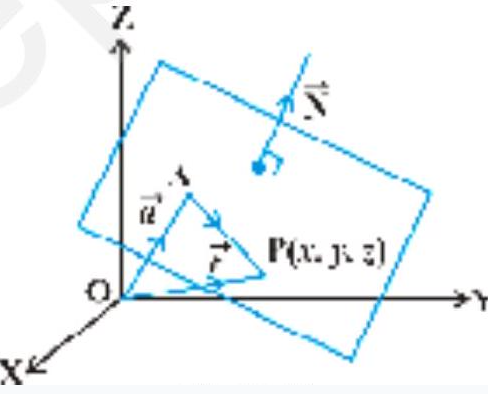
Fig 11.13

$$ \vec{a}=x_1 \hat{i}+y_1 \hat{j}+z_1 \hat{k}, \vec{r}=x \hat{i}+y \hat{j}+z \hat{k} \text { and } \overrightarrow{\mathrm{N}}=A\hat{i} +B\hat{j}+B\hat{k} $$

Now $$\quad(\vec{r}-\vec{a}) \cdot \overrightarrow{\mathrm{N}}=0$$ So $$\quad\left[\left(x-x_1\right) \hat{i}+\left(y-y_1\right) \hat{j}+\left(z-z_1\right) \hat{k}\right] \cdot(\mathrm{A} \hat{i}+\mathrm{B} \hat{j}+C \hat{k})=0$$ i.e. $$\quad \mathbf{A}\left(x-x_1\right)+\mathbf{B}\left(y-y_1\right)+\mathbf{C}\left(z-z_1\right)=\mathbf{0}$$

$$ \mathrm{A}\left(x-x_{1}\right)+\mathrm{B}\left(y-y_{1}\right)+\mathrm{C}\left(z-z_{1}\right)=0 $$

Example 17 Find the vector andcartesian equations of the plane which passesthrough thepoint (5, 2, -4) and perpendicular to the line with direction ratios 2, 3, -1

Solution We have the position vector of point $ (5, 2, – 4) \quad as \quad \vec{a}=5 \hat{i}+2\hat{j}-4 \hat{k} $ and the normal vector equation of the plane is given by $(\vec{r}-\vec{a}).N=0$

Therefore, the vector equation of the plane is given by $(\vec{r}-\vec{a}) \cdot \overrightarrow{\mathrm{N}}=0$

or $$ [\vec{r}-(5 \hat{i}+2 \hat{j}-4 \hat{k})] \cdot(2 \hat{i}+3 \hat{j}-\hat{k})=0 $$

Transforming (1) into Cart esian form, we have $ \begin{array}{ll} & {[(x-5) \hat{i}+(y-2) \hat{j}+(z+4) \hat{k}] \cdot(2 \hat{i}+3 \hat{j}-\hat{k})=0} \\ or & 2(x-5) +(y-2)+(z+4)= 0\\ i.e. & 2 x+3 y-z=20 \end{array} $

which is the cartesian equation of the plane.

11.6.3 Equation of a plane passing through three non collinear points

Let $\mathrm{R}, \mathrm{S}$ and $\mathrm{T}$ be three non collinear pointson the plane with position vectors $\vec{a}, \vec{b}$ and $\vec{c}$ respectively (Fig 11.14).

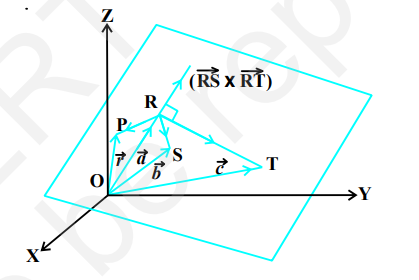
Fig 11.14 is

or

$$ \begin{array}{r} (\vec{r}-\vec{a}) \cdot(\overrightarrow{\mathrm{RS}} \times \overrightarrow{\mathrm{RT}})=0 \\ (\overrightarrow{\boldsymbol{r}}-\overrightarrow{\boldsymbol{a}}) \cdot[(\overrightarrow{\boldsymbol{b}}-\overrightarrow{\boldsymbol{a}}) \times(\overrightarrow{\boldsymbol{c}}-\overrightarrow{\boldsymbol{a}})]=\mathbf{0} \tag{1} \end{array} $$

This is the equation of the plane in vector form passing through three noncollinear points.

$\square$ Note Why wasit necessary to say that the three points hadto be non collinear? If the three points were on the same line, then there will be many planes that will contain them (Fig11.15).

These planeswill resemble the pages of a book where the line containing the pointsR, Sand T are membersin the binding of the book.

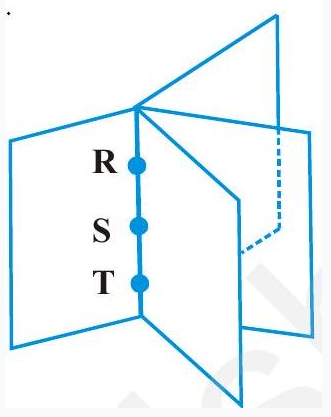
Fig 11.15

Cartesian form

Let $\left(x_{1}, y_{1}, z_{1}\right),\left(x_{2}, y_{2}, z_{2}\right)$ and $\left(x_{3}, y_{3}, z_{3}\right)$ be the coordinates of the points $\mathrm{R}, \mathrm{S}$ and $\mathrm{T}$ respectively. Let $(x, y, z)$ be the coordinates of any point $\mathrm{P}$ on the planewith position vector $\vec{r}$. Then

$$ \begin{aligned} & \overrightarrow{\mathrm{RP}}=\left(x-x_1\right) \hat{i}+\left(y-y_1\right) \hat{j}+\left(z-z_1\right) \hat{k} \end{aligned} $$

$$ \begin{aligned} & \overrightarrow{\mathrm{RS}}=\left(x_2-x_1\right) \hat{i}+\left(y_2-y_1\right) \hat{j}+\left(z_2-z_1\right) \hat{k} \end{aligned} $$

Substitutingthese valuesin equation (1) of thevector form and expressing it in the form of a determinant, we have

$$ \left|\begin{array}{lll} x-x_{1} & y-y_{1} & z-z_{1} \\ x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\ x_{3}-x_{1} & y_{3}-y_{1} & z_{3}-z_{1} \end{array}\right|=0 $$

which is the equation of the plane in Cartesian form passingthrough three non collinear points $\left(x_{1}, y_{1}, z_{1}\right),\left(x_{2}, y_{2}, z_{2}\right)$ and $\left(x_{3}, y_{3}, z_{3}\right)$.

Example 18 Find the vector equations of the plane passing through the points R(2,5,-3), S(-2,-3) and T(5,3,-3)

Solution Let $ \vec{a}=2 \hat{i}+5 \hat{j}-3 \hat{k},\quad \vec{b}=-2 \hat{i}-3 \hat{j}+5 \hat{k},\quad \vec{c}=5 \hat{i}+3 \hat{j}-3 \hat{k} $

Then the vector equation of the plane passing through $\vec{a}, \vec{b}$ and $\vec{c}$ and is given by

$$ \begin{aligned} & (\vec{r}-\vec{a}) \cdot(\overrightarrow{\mathrm{RS}} \times \overrightarrow{\mathrm{RT}})=0 \quad (Why?) \\ \quad & (\vec{r}-\vec{a}) \cdot[(\vec{b}-\vec{a}) \times(\vec{c}-\vec{a})]=0 \\ i.e. \quad \quad \quad \quad \quad \quad [\vec{r}-2 \hat{i}+5 \hat{j}-3 \hat{k}] \end{aligned} $$

11.6.4 Intercept form of the equation of a plane

In this section, we shall deduce the equation of a plane in termsof the intercepts made by the planeon the coordinate axes. Let the equation of the plane be

$$ \begin{equation*} \mathrm{A} x+\mathrm{B} y+\mathrm{Cz}+\mathrm{D}=0(\mathrm{D} \neq 0) \tag{1} \end{equation*} $$

Let the plane make intercepts $a, b, c$ on $x, y$ and $z$ axes, respectively (Fig 11.16).

Hence, the plane meets $x, y$ and $z$-axes at $(a, 0,0)$, $(0, b, 0),(0,0, c)$, respectively.

Therefore

$$ \begin{aligned} & \mathrm{A} a+\mathrm{D}=0 \text { or } \mathrm{A}=\frac{\mathrm{D}}{a} \\ & \mathrm{~B} b+\mathrm{D}=0 \text { or } \mathrm{B}=\frac{\mathrm{D}}{b} \\ & \mathrm{C} c+\mathrm{D}=0 \text { or } \mathrm{C}=\frac{\mathrm{D}}{c} \end{aligned} $$

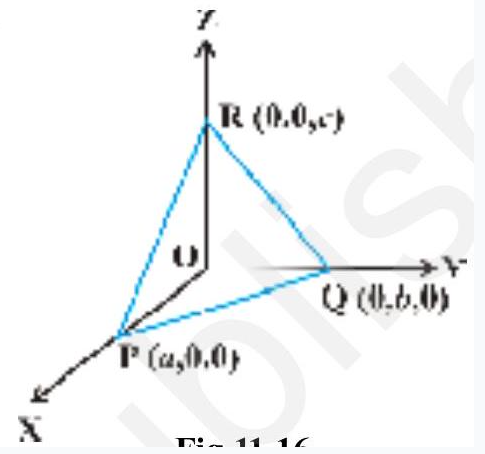
Fig 11.16

Substituting these values in the equation (1) of the plane and simplifying, weget

$$ \begin{equation*} \frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1 \tag{1} \end{equation*} $$

which is the required equation of the plane in the intercept form.

Example 19 Find the equation of the plane with intercepts 2,3 and 4 on the $x, y$ and $z$-axis respectively.

Solution Let the equation of the plane be

$$ \begin{equation*} \frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1 \tag{1} \end{equation*} $$

Here

$$ a=2, b=3, c=4 \text {. } $$

Substituting the values of $a, b$ and $c$ in (1), we get the required equation of the plane as $\frac{x}{2}+\frac{y}{3}+\frac{z}{4}=1$ or $6 x+4 y+3 z=12$.

11.6.5 Plane passing thro ugh the intersection of two given planes

Let $\pi_1$ and $\pi_2$ be two planes with equations $\vec{r} \bullet \hat{n}_1=d_1$ and $\vec{r} \bullet \hat{n}_2=d_2$ respectively. Theposition vector of any point on the line of intersection must satisfy both the equations(Fig 11.17).

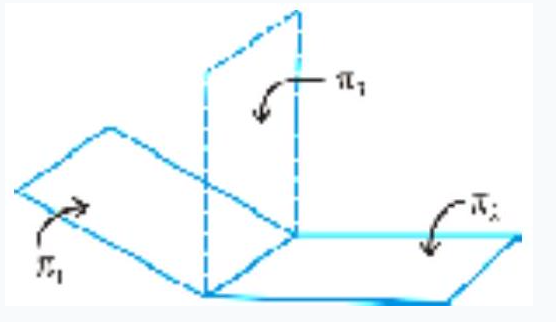
Fig 11.17

If $\vec{t}$ is the position vector of a point on the line, then

$$ \vec{t} \cdot \hat{n_1}=d_1 \quad \text{and} \quad \vec{t} \cdot \hat{n_2} d_{2} $$

Therefore, for all real values of $\lambda$, we have

$$ \vec{t} \cdot (\hat{n_1} + \lambda \hat{n_2})=d_1 + \lambda d_2 $$

Since $\vec{t}$ isarbitrary, it satisfies for any point on the line.

Hence, the equation $ \vec{t} \cdot (\hat{n_1} + \lambda \hat{n_2})=d_1 + \lambda d_2 $ represents a plane $\pi_{3}$ which is such that if any vector $\vec{r}$ satisfies both the equations $\pi_{1}$ and $\pi_{2}$, it also satisfies the equation $\pi_{3}$ i.e., any plane passingthrough the intersection of the planes

$$ \vec{r} \cdot \hat{n_1}=d_1 \quad \text{and} \quad \vec{r} \cdot \hat{n_2} d_{2} $$ has the equation $$ \vec{r} \cdot (\hat{n_1} + \lambda \hat{n_2})=d_1 + \lambda d_2 $$

Cartesian form

In Cartesian system, let

$$ \begin{aligned} \vec{n}_1 & =\mathrm{A}_1 \hat{i}+\mathrm{B}_2 \hat{j}+\mathrm{C}_1 \hat{k} \\ \vec{n}_2 & =\mathrm{A}_2 \hat{i}+\mathrm{B}_2 \hat{j}+\mathrm{C}_2 \hat{k} \\ \text { and } \quad \vec{r} & =x \hat{i}+y \hat{j}+z \hat{k} \end{aligned} $$ and Then (1) becomes $$ x\left(\mathrm{~A}_1+\lambda \mathrm{A}_2\right)+y\left(\mathrm{~B}_1+\lambda \mathrm{B}_2\right)+z\left(\mathrm{C}_1+\lambda \mathrm{C}_2\right)=d_1+\lambda d_2 $$ or $$ \left(\mathrm{A}_1 x+\mathrm{B}_1 y+\mathrm{C}_1 z-d_1\right)+\lambda\left(\mathrm{A}_2 x+\mathrm{B}_2 y+\mathrm{C}_2 z-d_2\right)=0 $$

which is the required Cartesian form of the equation of the plane passing through the intersection of the given planesfor each value of $\lambda$

Example 20 Find the vector equation of theplane passingthrough the intersection of theplanes $\vec{r} \cdot\left(\hat{i} + \hat{j} + \hat{k}\right)=6$ and $\vec{r} \cdot\left(2 \hat{i} + 3 \hat{j} + 4 \hat{k}\right)=-5$, and the point $(1,1,1)$.

Solution Here, $\vec{n}_1=\hat{i} + \hat{j} + \hat{k} \quad \text{and} \quad \vec{n}_2= 2 \hat{i} + 3 \hat{j} + 4 \hat{k}$

and

$$ d_{1}=6 \text { and } d_{2}= -5 $$

Hence, using the relation $\vec{r} \cdot (\vec{n_1} + \lambda\vec{n_2})=d_{2} $, we get $$ \vec{r} \cdot[\hat{i}+\hat{j}+\hat{k}+\lambda(2\hat{i}+3\hat{j}+4\hat{k})]=6-5\lambda $$

or $$ \vec{r} \cdot[(1+2\lambda)\hat{i}+(1+3\lambda)\hat{j}+(1+4\lambda)\hat{k}]=6-5\lambda $$

where, $\lambda$ is some real number.

Taking

$$\vec{r}=x\hat{i}+y\hat{j}+z\hat{k} $$, we get

or $$x\hat{i}+y\hat{j}+z\hat{k} \cdot [(1+2\lambda)\hat{i}+(1+3\lambda)\hat{j}+(1+4\lambda)\hat{k}]=6-5\lambda $$

or $$ (1+2\lambda)\hat{i}+(1+3\lambda)\hat{j}+(1+4\lambda)\hat{k}=6-5\lambda $$

$$(x + y + z - 6)+\lambda(2x+3y+4z+5)=0$$

Given that the plane passesthrough the point ( $1,1,1)$, it must satisfy (2), i.e.

$$ (1+1+1 - 6)+\lambda(2+3+4+5)=0 $$

or

$$ \lambda=\frac{3}{14} $$

Putting the values of $\lambda$ in (1), we get $$ \vec{r}\left[\left(1+\frac{3}{7}\right) \hat{i}+\left(1+\frac{9}{14}\right) \hat{j}+\left(1+\frac{6}{7}\right) \hat{k}\right]=6-\frac{15}{14} $$ or $$ \vec{r}\left(\frac{10}{7} \hat{i}+\frac{23}{14} \hat{j}+\frac{13}{7} \hat{k}\right)=\frac{69}{14} $$ or $$ \vec{r} \cdot(20 \hat{i}+23 \hat{j}+26 \hat{k})=69 $$ which is the required vector equat ion of the plane.

11.7 Coplanarity of Two Lines

Let the given lines be $$ \begin{aligned} & \vec{r}=\vec{a}_1+\lambda \vec{b}_1 \\ & \vec{r}=\vec{a}_2+\mu \vec{b}_2 \end{aligned} $$ and Theline (1)passesthrough the point, say A, with position vect or $\vec{a}_1$ andisparallel to $\vec{b}_1$. The line (2) passes through the point, say $B$ with position vector $\vec{a}_2$ and is parallel to $\vec{b}_2$.

Thus, $$ \overrightarrow{\mathrm{AB}}=\vec{a}_2 \vec{a}_1 $$

The given lines are coplanar if and only if $\overrightarrow{\mathrm{AB}}$ is perpendicular to $\vec{b}_1 \times \vec{b}_2$. i.e. $$ \overrightarrow{\mathrm{AB}} \cdot\left(\vec{b}_1 \times \vec{b}_2\right)=0 \text { or }\left(\vec{a}_2-\vec{a}_1\right) \cdot\left(\vec{b}_1 \times \vec{b}_2\right)=0 $$

Cartesian form

Let $\left(x_{1}, y_{1}, z_{1}\right)$ and $\left(x_{2}, y_{2}, z_{2}\right)$ be the coordinates of the points $\mathrm{A}$ and $\mathrm{B}$ respectively.

Let $a_{1}, b_{1}, c_{1}$ and $a_{2}, b_{2}, c_{2}$ be the direction ratios of $\vec{b}{1}$ and $\vec{b}{2}$, respectively. Then

$$ \begin{aligned} & \left.\overrightarrow{\mathrm{AB}}=(x_2-\bar{x}_1\right) \hat{i}+\left(y_2-y_1\right) \hat{j}+\left(z_2-\bar{z}_1\right) \hat{k} \\ & \vec{b}_1=\bar{a}_1 \hat{i}+b_1 \hat{j}+c_1 \hat{k} \text { and } \vec{b}_2 \bar{a}_2 \hat{i}+b_2 \hat{j}+c_2 \hat{k} \end{aligned} $$

The given lines are coplanar if andonly if $\overrightarrow{\mathrm{AB}} \cdot\left(\vec{b}_1 \times \vec{b}_2\right)=0$. In the cart esian form, it can be expressed as

$$ \left|\begin{array}{ccc} x_2 x_1 & y_2 y_1 & z_2 z_1 \\ a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \end{array}\right| = 0 $$

Example 21 Showthat thelines

$$ \frac{x+3}{- 3}=\frac{y-1}{1}=\frac{z-5}{5} \text { and } \frac{x+1}{- 1}=\frac{y-2}{2}=\frac{z-5}{5} \text { are coplanar. } $$

Solution Here, $x_{1}=$ -3, $y_{1}=1, z_{1}=5, a_{1}=- 3, b_{1}=1, c_{1}=5$

$$ x_{2}=- 1, y_{2}=2, z_{2}=5, a_{2}=- 1, b_{2}=2, c_{2}=5 $$

Now consider the determinant

$$ \left|\begin{array}{ccc} x_2 -x_ 1 & y_2 -y_1 & z_2 -z_1 \\ a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \end{array}\right|=\left|\begin{array}{ccc} 2 & 1 & 0 \\ 3 & 1 & 5 \\ 1 & 2 & 5 \end{array}\right|=0 $$

Therefore, lines are coplanar.

11.8 Angle between Two Planes

Definition 2 The angle between two planes is defined as the angle between their normals (Fig 11.18 (a)). Observe that if $\theta$ is an angle bet ween the two planes, then so is 180 -$\theta$ (Fig 11.18 (b)). We shall take the acute angle as the angles between two planes.

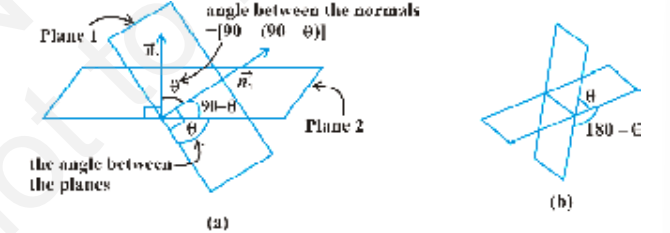
Fig 11.18

If $\vec{n_1}$ and $\vec{n}_{2}$ are normals to the planes and $\theta$ be the angle between the planes

$$ \vec{r} \cdot \vec{n_1}=d_1 \text { and } \vec{r} \cdot \vec{n_2}=d_2 $$

Then $\theta$ isthe angle between thenormals to the planes drawn from some common point.

We have,

$$ \cos \theta=\left|\frac{\vec{n_1} \cdot \vec{n_2}}{\left|\vec{n_1}\right|\left|\vec{n_2}\right|}\right| $$

Note The planes are perpendicular to each other if $\vec{n_1} \cdot \vec{n_2}=0$ and parallel if $\vec{n_1}$ is parallel to $\vec{n_2}$.

Cartesian form Let $\theta$ be the angle between the planes,

$$ \mathrm{A_1} x+\mathrm{B_1} y+\mathrm{C_1} z+\mathrm{D_1}=0 \text { and } \mathrm{A_2} x+\mathrm{B_2} y+\mathrm{C_2} z+\mathrm{D_2}=0 $$

The direction ratios of the normal to the planes are $A_{1}, B_{1}, C_{1}$ and $A_{2}, B_{2}, C_{2}$ respectively.

Therefore, $$ \cos \theta=\left|\frac{A_1 A_2+B_1B_2+C_1C_2}{\sqrt{A_1^2 + B_1^2+C_1^2}\sqrt{A_2^2 + B_2^2+C_2^2}}\right| $$

Note

1. If the planes are at right angles, then $\theta=90^{\circ}$ and so $\cos \theta=0$. Hence, $\cos \theta=\mathrm{A_1} \mathrm{~A_2}+\mathrm{B_1} \mathrm{~B_2}+\mathrm{C_1} \mathrm{C_2}=0$.
2. If the planesare parallel, then $\frac{A_{1}}{A_{2}}=\frac{B_{1}}{B_{2}}=\frac{C_{1}}{C_{2}}$.

Example 22 Find the angle between the two planes 2x+y-2z=5 and 3x-6y-2z=7 using vector method.

Solution Theanglebet ween two planes is the angle between their normals. From the equation of the planes, the normal vectorsare

Therefore

$$ \vec{N_1}=2\hat{i}+\hat{j}-2\hat{k} \quad \vec{N_2}=3\hat{i}-6\hat{j}-2\hat{k} $$

$$ \cos \theta=\left|\frac{\vec{N_1} \cdot \vec{N_2}}{|\vec{N_1}||\vec{N_2|}}\right|=\left|\frac{(2\hat{i}+\hat{j}-2\hat{k})\cdot (3\hat{i}-6\hat{j}-2\hat{k})}{\sqrt{4+1+4}\sqrt{9+36+4}} \right|=\left(\frac{4}{21}\right) $$

Hence

$$ \theta=\cos ^{-1}\left(\frac{4}{21}\right) $$

Example 23 Find the angle bet ween the two planes $3 x$ - $6 y+2 z=7$ and $2 x+2 y$ - $2 z=5$.

Solution Comparing the given equations of the planeswith the equations

We get

$$ \begin{aligned} \mathrm{A_1} x+\mathrm{B_1} y+\mathrm{C_1} z+\mathrm{D_1}=0 \text { and } \mathrm{A_2} x+\mathrm{B_2} y+\mathrm{C_2} z+\mathrm{D_2}=0 \\ \mathrm{~A_1}=3, \mathrm{~B_1}= -6, \mathrm{C_1}=2 \\ \mathrm{~A_2}=2, \mathrm{~B_2}=2, \mathrm{C_2}=- 2 \end{aligned} $$

Therefore, $\quad \theta=\cos ^{-1}\left(\frac{5 \sqrt{3}}{21}\right)$

11.9 Distance of a Point from a Plane

Vector form

Consider a point $\mathrm{P}$ with position vector $\vec{a}$ and a plane $\pi_{1}$ whose equation is $\vec{r} \cdot \hat{\mathbf{E}}=d$ (Fig 11.19).

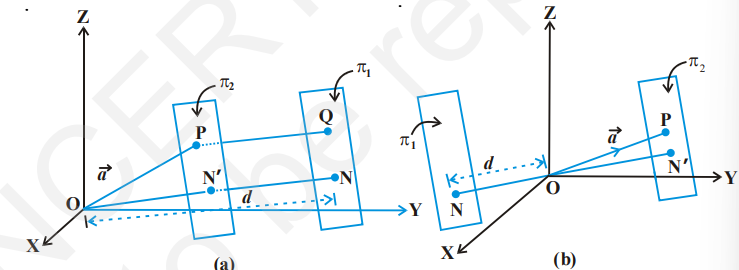
Fig 11.19

Consider a plane $\pi_{2}$ through $\mathrm{P}$ parallel to the plane $\pi_{1}$. The unit vector normal to $\pi_{2}$ is $\hat{n}$. Hence, its equation is $(\vec{r}-\vec{a}) \cdot \hat{n}=0$

i.e., $\quad \vec{r} \cdot \hat{n}=\vec{a} \cdot \hat{n}$

Thus, the distance ON’ of this plane from the origin is $| \vec{a} \cdot \hat{n}|$. Therefore, the distance PQ from the plane $\pi_{1}$ is (Fig. 11.21(a))

i.e.,

$$\mathrm{ON} \quad \mathrm{ON}^{\prime}=|d - \vec{a} \cdot \hat{n}|$$ which isthe length of the perpendicular from apoint to the given plane.

We may establish the similar results for (Fig 11.19(b)).

Note

1. If the equationof the plane $\pi_{2}$ is in the form $\vec{r} \cdot \overrightarrow{\mathrm{N}} \fallingdotseq d$, where $\overrightarrow{\mathrm{N}}$ isnormal to the plane, then the perpendicular distance is $\frac{|\vec{a} \cdot \overrightarrow{\mathrm{N}}-d|}{|\overrightarrow{\mathrm{N}}|}$.
2. The length of the perpendicular from origin Oto the plane $\vec{r} \cdot \overrightarrow{\mathrm{N}} \leftrightharpoons d$ is $\frac{|d|}{|\overrightarrow{\mathrm{N}}|}$ (since $\vec{a}=0$ ).

Cartesian form

Let $\mathrm{P}\left(x_{1}, y_{1}, z_{1}\right)$ bethe given point with position vector $\vec{a}$ and

$$ \mathrm{A} x+\mathrm{B} y+\mathrm{C} z=\mathrm{D} $$

be the Cartesian equation of the given plane. Then

$$ \begin{aligned} \vec{a} & =x_{1} \hat{i} +y_{1}\hat{j}+z_{1}\hat{k} \\ \overrightarrow{\mathrm{N}} & =\mathrm{A} \hat{i} + \mathrm{B} + \mathrm{C} \hat{k} \end{aligned} $$

Hence, from Note 1, the perpendicular from $P$ to the plane is

$$ \begin{aligned} & \left|\frac{(x_{1} \hat{i} +y_{1}\hat{j}+z_{1}\hat{k})\cdot(\mathrm{A} \hat{i} + \mathrm{B} + \mathrm{C} \hat{k})}{\sqrt{A^2+B^2+C^2}}\right| \end{aligned} $$

$$ \begin{aligned} =& \left|\frac{Ax_1+By_1+Cz_1-D}{\sqrt{A^2+B^2+C^2}}\right| \end{aligned} $$

Example 24 Find the distance of a point (2, 5, -3) from the plane

$$ \vec{r} \cdot\left(6 \hat{i}_{-}-3 \hat{j}+2 \hat{k}\right)=4 $$

Solution Here, $\vec{a}=2 \hat{i}+5 \hat{j}-3 \hat{k}, \overrightarrow{\mathrm{N}}=\hat{i}-3 \hat{j}+2\hat{k}$ and $d=4$.

Therefore, the distance of the point $(2,5, \bar{i} 3)$ from the given plane is

11.10 Angle between a Line and a Plane

Definition 3 The angle between a line and aplane is the complement of the angle between the line and normal to the plane(Fig 11.20).

Vector form If the equation of the line is $\vec{r}=\vec{a}+\lambda \vec{b}$ and the equation of the plane is $\vec{r} \cdot \vec{n}=d$. Then the angle $\theta$ bet ween the line andthe

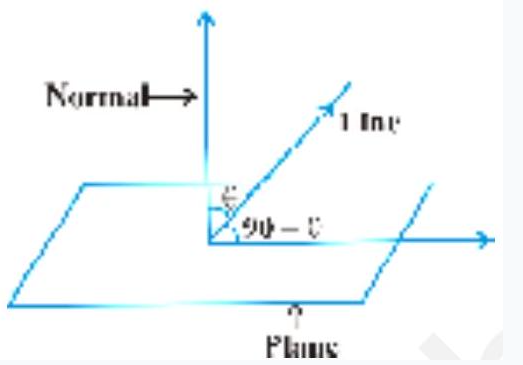
Fig 11.20 normalto the planeis

$$ \cos \theta=\left|\frac{\vec{b} \cdot \vec{n}}{|\vec{b}| \cdot|\vec{n}|}\right| $$

and so the angle $\phi$ bet ween the line and the plane is given by $90 \mathrm{i} \theta$, i.e.,

$$ \begin{aligned} \sin (90 - \theta) & =\cos \theta \ \sin \phi & =\left|\frac{\vec{b} \cdot \vec{n}}{|\vec{b}||\vec{n}|}\right| \text { or } \phi=\sin ^{i 1}\left|\frac{\bar{b} \cdot \bar{n}}{|\vec{b}||\bar{n}|}\right| \end{aligned} $$

i.e.

Example 25 Find the angle bet ween the line

$$ \frac{x+1}{2}=\frac{y}{3}=\frac{z-3}{6} $$

and the plane 10 x+2 yi -11 z=3.

Solution Let $\theta$ be the angle between the line and thenormal to theplane. Converting the given equations into vect or form, we have

$$ \vec{r}=(-\hat{i}+3 \hat{k})+\lambda(2 \hat{i}+3 \hat{j}+6 \hat{k}). $$

and

$$ \vec{r} \cdot(10 \hat{i}+2 \hat{j}-11\hat{k})=3 $$

Here

$$ \begin{aligned} & \vec{b}=2 \hat{i}+3 \hat{j}+6 \hat{k} \text { and } \vec{n}=10 \hat{i}=2 \hat{j}-11 \hat{k} \end{aligned} $$

$$ \sin\theta=\left|\frac{(2 \hat{i}+3 \hat{j}+6 \hat{k})\cdot(10 \hat{i}=2 \hat{j}-11 \hat{k})}{\sqrt{2^2+3^2+6^2}\sqrt{10^2+2^2+11^2}}\right| $$

$$ \begin{aligned} & =\left|\frac{-40}{7 \times 15}\right|=\left|\frac{-8}{21}\right|=\frac{8}{21} \quad \text { or } \phi=\sin ^{-1}\left(\frac{8}{21}\right) \end{aligned} $$

EXERCISE 11.3

1. In each of the followingcases, determine the direction cosines of the normal to the plane and the distance from the origin.

(a) z=2 $\quad\quad$ (b) x+y+z=1

(c) 2 x+3 y -z=5 $\quad\quad$ (d) 5 y+8=0

Solution

(a) The equation of the plane is $z=2$ or $0 x+0 y+z=2 \ldots$ (1)

The direction ratios of normal are 0,0 , and 1 .

$\therefore \sqrt{0^{2}+0^{2}+1^{2}}=1$

Dividing both sides of equation (1) by 1 , we obtain

$0 . x+0 . y+1 . z=2$

This is of the form $I x+m y+n z=d$, where $l, m, n$ are the direction cosines of normal to the plane and $d$ is the distance of the perpendicular drawn from the origin.

Therefore, the direction cosines are 0,0 , and 1 and the distance of the plane from the origin is 2 units.

(b) $x+y+z=1 \ldots$ (1)

The direction ratios of normal are 1,1 , and 1 .

$\therefore \sqrt{(1)^{2}+(1)^{2}+(1)^{2}}=\sqrt{3}$

Dividing both sides of equation (1) by $\sqrt{3}$, we obtain

$\frac{1}{\sqrt{3}} x+\frac{1}{\sqrt{3}} y+\frac{1}{\sqrt{3}} z=\frac{1}{\sqrt{3}}$

This equation is of the form $l x+m y+n z=d$, where $l, m, n$ are the direction cosines of normal to the plane and $d$ is the distance of normal from the origin.

Therefore, the direction cosines of the normal are $\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}$, and $\frac{1}{\sqrt{3}}$ and the distance of normal from the origin is $\frac{1}{\sqrt{3}}$ units.

(c) $2 x+3 y-z=5$

The direction ratios of normal are 2,3 , and -1 .

$\therefore \sqrt{(2)^{2}+(3)^{2}+(-1)^{2}}=\sqrt{14}$

Dividing both sides of equation (1) by $\sqrt{14}$, we obtain

$\frac{2}{\sqrt{14}} x+\frac{3}{\sqrt{14}} y-\frac{1}{\sqrt{14}} z=\frac{5}{\sqrt{14}}$

This equation is of the form $l x+m y+n z=d$, where $l, m, n$ are the direction cosines of normal to the plane and $d$ is the distance of normal from the origin.

Therefore, the direction cosines of the normal to the plane are $\frac{2}{\sqrt{14}}, \frac{3}{\sqrt{14}}$, and $\frac{-1}{\sqrt{14}}$ and

the distance of normal from the origin is $\frac{5}{\sqrt{14}}$ units.

(d) $5 y+8=0$

$\Rightarrow 0 x-5 y+0 z=8$

The direction ratios of normal are $0,-5$, and 0 .

$\therefore \sqrt{0+(-5)^{2}+0}=5$

Dividing both sides of equation (1) by 5 , we obtain

$-y=\frac{8}{5}$

This equation is of the form $l x+m y+n z=d$, where $l, m, n$ are the direction cosines of normal to the plane and $d$ is the distance of normal from the origin.

Therefore, the direction cosines of the normal to the plane are $0,-1$, and 0 and the

distance of normal from the origin is $\frac{8}{5}$ units.

2. Find the vector equation of a plane which is at a distance of 7 units from the origin and normal to thevector $3 \hat{i}+ 5 \hat{j}-6 \hat{k}$

Solution

The normal vector is, $\vec{n}=3 \hat{i}+5 \hat{j}-6 \hat{k}$

$\therefore \hat{n}=\frac{\vec{n}}{|\vec{n}|}=\frac{3 \hat{i}+5 \hat{j}-6 \hat{k}}{\sqrt{(3)^{2}+(5)^{2}+(6)^{2}}}=\frac{3 \hat{i}+5 \hat{j}-6 \hat{k}}{\sqrt{70}}$

It is known that the equation of the plane with position vector $\vec{r}$ is given by, $\vec{r} \cdot \hat{n}=d$

$\Rightarrow \hat{r} \cdot(\frac{3 \hat{i}+5 \hat{j}-6 \hat{k}}{\sqrt{70}})=7$

This is the vector equation of the required plane.

3. Find the Cartesian equation of the following planes:

(a) $\vec{r} \cdot\left(\hat{i} + \hat{j}-\hat{k}\right)=2$ $\quad\quad$(b) $\vec{r} \cdot(2 \hat{i}+3 \hat{j}-4 \overline{j})=1$

(c) $\vec{r} \cdot\left[(s-2 t) \hat{i}(3-t) \hat{j}_{+}(2 s+t) \hat{k}=15\right].$

Solution

(a) It is given that equation of the plane is

$\vec{r} \cdot(\hat{i}+\hat{j}-\hat{k})=2$

For any arbitrary point $P(x, y, z)$ on the plane, position vector $\vec{r}$ is given by, $\vec{r}=x \hat{i}+y \hat{j}-z \hat{k}$

Substituting the value of $\vec{r}$ in equation (1), we obtain

$(x \hat{i}+y \hat{j}-z \hat{k}) \cdot(\hat{i}+\hat{j}-\hat{k})=2$

$\Rightarrow x+y-z=2$

This is the Cartesian equation of the plane.

(b) $\vec{r} \cdot(2 \hat{i}+3 \hat{j}-4 \hat{k})=1$

For any arbitrary point $P(x, y, z)$ on the plane, position vector $\vec{r}$ is given by,

$\vec{r}=x \hat{i}+y \hat{j}-z \hat{k}$

Substituting the value of $\vec{r}$ in equation (1), we obtain

$(x \hat{i}+y \hat{j}+z \hat{k}) \cdot(2 \hat{i}+3 \hat{j}-4 \hat{k})=1$

$\Rightarrow 2 x+3 y-4 z=1$

This is the Cartesian equation of the plane.

(c) $\vec{r} \cdot[(s-2 t) \hat{i}+(3-t) \hat{j}+(2 s+t) \hat{k}]=15$

For any arbitrary point $P(x, y, z)$ on the plane, position vector $\vec{r}$ is given by, $\vec{r}=x \hat{i}+y \hat{j}-z \hat{k}$

Substituting the value of $\vec{r}$ in equation (1), we obtain

$(x \hat{i}+y \hat{j}-z \hat{k}) \cdot[(s-2 t) \hat{i}+(3-t) \hat{j}+(2 s+t) \hat{k}]=15$

$\Rightarrow(s-2 t) x+(3-t) y+(2 s+t) z=15$

This is the Cartesian equation of the given plane.

4. In the following cases, find the coordinates of the foot of the perpendicular drawn from theorigin.

(a) $2 x+3 y+4 +z12=0$ $\quad\quad$(b) $3 y+4 z - 6=0$

(c) $x+y+z=1$ $\quad\quad$(d) $5 y+8=0$

Solution

(a) Let the coordinates of the foot of perpendicular $P$ from the origin to the plane be $(x_1, y_1, z_1)$. $2 x+3 y+4 z-12=0$

$\Rightarrow 2 x+3 y+4 z=12$

The direction ratios of normal are 2, 3, and 4 .

$\therefore \sqrt{(2)^{2}+(3)^{2}+(4)^{2}}=\sqrt{29}$

Dividing both sides of equation (1) by $\sqrt{29}$, we obtain

$\frac{2}{\sqrt{29}} x+\frac{3}{\sqrt{29}} y+\frac{4}{\sqrt{29}} z=\frac{12}{\sqrt{29}}$

This equation is of the form $l x+m y+n z=d$, where $l, m, n$ are the direction cosines of normal to the plane and $d$ is the distance of normal from the origin.

The coordinates of the foot of the perpendicular are given by

( $l d, m d, n d)$.

Therefore, the coordinates of the foot of the perpendicular are

$(\frac{2}{\sqrt{29}} \cdot \frac{12}{\sqrt{29}}, \frac{3}{\sqrt{29}} \cdot \frac{12}{\sqrt{29}}, \frac{4}{\sqrt{29}} \cdot \frac{12}{\sqrt{29}})$ i.e., $(\frac{24}{29}, \frac{36}{49}, \frac{48}{29})$.

(b) Let the coordinates of the foot of perpendicular $P$ from the origin to the plane be ( $x_1$, $.y_1, z_1)$.

$3 y+4 z-6=0$

$\Rightarrow 0 x+3 y+4 z=6$

The direction ratios of the normal are 0,3 , and 4 .

$\therefore \sqrt{0+3^{2}+4^{2}}=5$

Dividing both sides of equation (1) by 5 , we obtain

$0 x+\frac{3}{5} y+\frac{4}{5} z=\frac{6}{5}$

This equation is of the form $l x+m y+n z=d$, where $l, m, n$ are the direction cosines of normal to the plane and $d$ is the distance of normal from the origin.

The coordinates of the foot of the perpendicular are given by

(Id, $m d, n d)$.

Therefore, the coordinates of the foot of the perpendicular are

$(0, \frac{3}{5}, \frac{6}{5}, \frac{4}{5} . \frac{6}{5})$ i.e., $(0, \frac{18}{25}, \frac{24}{25})$.

(c) Let the coordinates of the foot of perpendicular $P$ from the origin to the plane be ( $x_1$, $.y_1, z_1)$.

$x+y+z=1$

The direction ratios of the normal are 1,1 , and 1 .

$\therefore \sqrt{1^{2}+1^{2}+1^{2}}=\sqrt{3}$

Dividing both sides of equation (1) by $\sqrt{3}$, we obtain

$\frac{1}{\sqrt{3}} x+\frac{1}{\sqrt{3}} y+\frac{1}{\sqrt{3}} z=\frac{1}{\sqrt{3}}$

This equation is of the form $l x+m y+n z=d$, where $l, m, n$ are the direction cosines of normal to the plane and $d$ is the distance of normal from the origin.

The coordinates of the foot of the perpendicular are given by

( $l d, m d, n d)$.

Therefore, the coordinates of the foot of the perpendicular are

$(\frac{1}{\sqrt{3}} \cdot \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}} \cdot \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}} \cdot \frac{1}{\sqrt{3}})$ i.e., $(\frac{1}{3}, \frac{1}{3}, \frac{1}{3})$.

(d) Let the coordinates of the foot of perpendicular $P$ from the origin to the plane be ( $x_1$, $.y_1, z_1)$.

$5 y+8=0$

$\Rightarrow 0 x-5 y+0 z=8$

The direction ratios of the normal are $0,-5$, and 0 . $\therefore \sqrt{0+(-5)^{2}+0}=5$

Dividing both sides of equation (1) by 5 , we obtain

$-y=\frac{8}{5}$

This equation is of the form $l x+m y+n z=d$, where $l, m, n$ are the direction cosines of normal to the plane and $d$ is the distance of normal from the origin.

The coordinates of the foot of the perpendicular are given by

(Id, $m d, n d)$.

Therefore, the coordinates of the foot of the perpendicular are

$ (0,-1(\frac{8}{5}), 0) \text{ i.e., }(0,-\frac{8}{5}, 0) \text{. } $

5. Find the vector and cartesian equations of the planes

(a) that passes through the point (1,0,-2)nand the normal to the plane is $\hat{i}+\hat{\hat{j}}-\overline{\hat{k}}$

(b) that passes through the point $(1,4,6)$ and the normalvect or to the plane is $\hat{i} + 2 \hat{j}+\hat{k}$.

Solution

(a) The position vector of point $(1,0,-2)$ is $\vec{a}=\hat{i}-2 \hat{k}$

The normal vector $\vec{N}$ perpendicular to the plane is $\vec{N}=\hat{i}+\hat{j}-\hat{k}$

The vector equation of the plane is given by, $(\vec{r}-\vec{a}) \cdot \vec{N}=0$

$\Rightarrow[\vec{r}-(\hat{i}-2 \hat{k})] \cdot(\hat{i}+\hat{j}-\hat{k})=0$

$\vec{r}$ is the position vector of any point $P(x, y, z)$ in the plane.

$\therefore \vec{r}=x \hat{i}+y \hat{j}+z \hat{k}$

Therefore, equation (1) becomes

$ \begin{aligned} & {[(x \hat{i}+y \hat{j}+z \hat{k})-(\hat{i}-2 \hat{k})] \cdot(\hat{i}+\hat{j}-\hat{k})=0} \\ & \Rightarrow[(x-1) \hat{i}+y \hat{j}+(z+2) \hat{k}] \cdot(\hat{i}+\hat{j}-\hat{k})=0 \\ & \Rightarrow(x-1)+y-(z+2)=0 \\ & \Rightarrow x+y-z-3=0 \\ & \Rightarrow x+y-z=3 \end{aligned} $

This is the Cartesian equation of the required plane.

(b) The position vector of the point $(1,4,6)$ is $\vec{a}=\hat{i}+4 \hat{j}+6 \hat{k}$

The normal vector $\vec{N}$ perpendicular to the plane is $\vec{N}=\hat{i}-2 \hat{j}+\hat{k}$

The vector equation of the plane is given by, $(\vec{r}-\vec{a}) \cdot \vec{N}=0$

$\Rightarrow[\vec{r}-(\hat{i}+4 \hat{j}+6 \hat{k})] \cdot(\hat{i}-2 \hat{j}+\hat{k})=0$

$\vec{r}$ is the position vector of any point $P(x, y, z)$ in the plane.

$\therefore \vec{r}=x \hat{i}+y \hat{j}+z \hat{k}$

Therefore, equation (1) becomes

$ \begin{aligned} & {[(x \hat{i}+y \hat{j}+z \hat{k})-(\hat{i}+4 \hat{j}+6 \hat{k})] \cdot(\hat{i}-2 \hat{j}+\hat{k})=0} \\ & \Rightarrow[(x-1) \hat{i}+(y-4) \hat{j}+(z-6) \hat{k}] \cdot(\hat{i}-2 \hat{j}+\hat{k})=0 \\ & \Rightarrow(x-1)-2(y-4)+(z-6)=0 \\ & \Rightarrow x-2 y+z+1=0 \end{aligned} $

This is the Cartesian equation of the required plane.

6. Findthe equations of the planes that passes through three points.

(a) (1,1,-1) , (6, 4, - 5), (- 4, -2, 3)

(b) (1,1,0),(1,2,1),(-2,2, -1)

Solution

(a) The given points are $A(1,1,-1), B(6,4,-5)$, and $C(-4,-2,3)$.

$ \begin{aligned} \begin{vmatrix} 1 & 1 & -1 \\ 6 & 4 & -5 \\ -4 & -2 & 3 \end{vmatrix} & =(12-10)-(18-20)-(-12+16) \\ & =2+2-4 \\ & =0 \end{aligned} $

Since A, B, C are collinear points, there will be infinite number of planes passing through the given points.

(b) The given points are A $(1,1,0), B(1,2,1)$, and $C(-2,2,-1)$.

$ \begin{vmatrix} 1 & 1 & 0 \\ 1 & 2 & 1 \\ -2 & 2 & -1 \end{vmatrix} =(-2-2)-(2+2)=-8 \neq 0 $

Therefore, a plane will pass through the points $A, B$, and $C$.

It is known that the equation of the plane through the points, $(x_1, y_1, z_1),(x_2, y_2, z_2)$, and

$ \begin{aligned} & (x_3, y_3, z_3), \text{ is } \\ & \begin{vmatrix} x-x_1 & y-y_1 & z-z_1 \\ x_2-x_1 & y_2-y_1 & z_2-z_1 \\ x_3-x_1 & y_3-y_1 & z_3-z_1 \end{vmatrix} =0 \\ & \Rightarrow \begin{vmatrix} x-1 & y-1 & z \\ 0 & 1 & 1 \\ -3 & 1 & -1 \end{vmatrix} =0 \\ & \Rightarrow(-2)(x-1)-3(y-1)+3 z=0 \\ & \Rightarrow-2 x-3 y+3 z+2+3=0 \\ & \Rightarrow-2 x-3 y+3 z=-5 \\ & \Rightarrow 2 x+3 y-3 z=5 \end{aligned} $

This is the Cartesian equation of the required plane.

7. Find the intercepts cut off by the plane $2 x+y - z=5$.

Solution

$2 x+y-z=5$

Dividing both sides of equation (1) by 5 , we obtain

$\begin{aligned} & \frac{2}{5} x+\frac{y}{5}-\frac{z}{5}=1 \\ & \Rightarrow \frac{x}{\frac{5}{2}}+\frac{y}{5}+\frac{z}{-5}=1 \quad …(2)\end{aligned} $

It is known that the equation of a plane in intercept form is $\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$, where $a, b, c$ are the intercepts cut off by the plane at $x, y$, and $z$ axes respectively.

Therefore, for the given equation,

$a=\frac{5}{2}, b=5$, and $c=-5$

Thus, the intercepts cut off by the plane are $\frac{5}{2}, 5$, and -5 .

8. Find the equation of the plane with intercept 3 on the $y$-axisandparallel to ZOX plane.

Solution

The equation of the plane $Z O X$ is

$y=0$

Any plane parallel to it is of the form, $y=a$

Since the $y$-intercept of the plane is 3 ,

$\therefore a=3$

Thus, the equation of the required plane is $y=3$

9. Find the equation of the plane through the intersection of the planes $3 x - y+2 z - 4=0$ and $x+y+z - 2=0$ and the point $(2,2,1)$.

Solution

The equation of any plane through the intersection of the planes,

$3 x-y+2 z-4=0$ and $x+y+z-2=0$, is

$(3 x-y+2 z-4)+\alpha(x+y+z-2)=0$, where $\alpha \in R$

The plane passes through the point $(2,2,1)$. Therefore, this point will satisfy equation (1).

$\therefore(3 \times 2-2+2 \times 1-4)+\alpha(2+2+1-2)=0$

$\Rightarrow 2+3 \alpha=0$

$\Rightarrow \alpha=-\frac{2}{3}$

Substituting $\alpha=-\frac{2}{3}$ in equation (1), we obtain

$(3 x-y+2 z-4)-\frac{2}{3}(x+y+z-2)=0$

$\Rightarrow 3(3 x-y+2 z-4)-2(x+y+z-2)=0$

$\Rightarrow(9 x-3 y+6 z-12)-2(x+y+z-2)=0$

$\Rightarrow 7 x-5 y+4 z-8=0$

This is the required equation of the plane.

10. Find the vector equation of the plane passing through the intersection of the planes $\vec{r} \cdot\left(2 \hat{i} + 2 \hat{j}-3 \hat{k}\right)=7, \vec{r} \cdot\left(2 \hat{i} + 5 \hat{j}+3 \hat{j}\right)=9$ andthrough the point $(2,1,3)$.

Solution

The equations of the planes are $\vec{r} \cdot(2 \hat{i}+2 \hat{j}-3 \hat{k})=7$ and $\vec{r} \cdot(2 \hat{i}+5 \hat{j}+3 \hat{k})=9$

$\Rightarrow \vec{r} \cdot(2 \hat{i}+2 \hat{j}-3 \hat{k})-7=0$

$\vec{r} \cdot(2 \hat{i}+5 \hat{j}+3 \hat{k})-9=0$

The equation of any plane through the intersection of the planes given in equations (1) and (2) is given by,

$[\vec{r} \cdot(2 \hat{i}+2 \hat{j}-3 \hat{k})-7]+\lambda[\vec{r} \cdot(2 \hat{i}+5 \hat{j}+3 \hat{k})-9]=0$, where $\lambda \in R$

$$ \begin{align*} & \vec{r} \cdot[(2 \hat{i}+2 \hat{j}-3 \hat{k})+\lambda(2 \hat{i}+5 \hat{j}+3 \hat{k})]=9 \lambda+7 \\ & \vec{r} \cdot[(2+2 \lambda) \hat{i}+(2+5 \lambda) \hat{j}+(3 \lambda-3) \hat{k}]=9 \lambda+7 \tag{3} \end{align*} $$

The plane passes through the point $(2,1,3)$. Therefore, its position vector is given by, $\vec{r}=2 \hat{i}+2 \hat{j}+3 \hat{k}$

Substituting in equation (3), we obtain

$ \begin{aligned} & (2 \hat{i}+\hat{j}-3 \hat{k}) \cdot[(2+2 \lambda) \hat{i}+(2+5 \lambda) \hat{j}+(3 \lambda-3) \hat{k}]=9 \lambda+7 \\ & \Rightarrow(2+2 \lambda)+(2+5 \lambda)+(3 \lambda-3)=9 \lambda+7 \\ & \Rightarrow 18 \lambda-3=9 \lambda+7 \\ & \Rightarrow 9 \lambda=10 \\ & \Rightarrow \lambda=\frac{10}{9} \end{aligned} $

Substituting $\lambda=\frac{10}{9}$ in equation (3), we obtain

$\vec{r} \cdot(\frac{38}{9} \hat{i}+\frac{68}{9} \hat{j}+\frac{3}{9} \hat{k})=17$

$\Rightarrow \vec{r} \cdot(38 \hat{i}+68 \hat{j}+3 \hat{k})=153$

This is the vector equation of the required plane.

11. Find the equation of the plane through the line of intersection of the planes $x+y+z=1$ and $2 x+3 y+4 z=5$ which is perpendicular to the plane $x - y+z=0$.

Solution

The equation of the plane through the intersection of the planes, $x+y+z=1$ and

$$ \begin{align*} & 2 x+3 y+4 z=5, \text{ is } \\ & (x+y+z-1)+\lambda(2 x+3 y+4 z-5)=0 \\ & \Rightarrow(2 \lambda+1) x+(3 \lambda+1) y+(4 \lambda+1) z-(5 \lambda+1)=0 \tag{1} \end{align*} $$

The direction ratios, $a_1, b_1, c_1$, of this plane are $(2 \lambda+1),(3 \lambda+1)$, and $(4 \lambda+1)$.

The plane in equation (1) is perpendicular to $x-y+z=0$

Its direction ratios, $a_2, b_2, c_2$, are $1,-1$, and 1 .

Since the planes are perpendicular,

$a_1 a_2+b_1 b_2+c_1 c_2=0$

$\Rightarrow(2 \lambda+1)-(3 \lambda+1)+(4 \lambda+1)=0$

$\Rightarrow 3 \lambda+1=0$

$\Rightarrow \lambda=-\frac{1}{3}$

Substituting $\lambda=-\frac{1}{3}$ in equation (1), we obtain

$\frac{1}{3} x-\frac{1}{3} z+\frac{2}{3}=0$

$\Rightarrow x-z+2=0$

This is the required equation of the plane.

12. Find the angle between the planes whose vector equations are

$\vec{r} \cdot (2 \hat{i} + 2 \hat{j}-3 \hat{k}) \quad \text{and} \quad \vec{r} \cdot (3 \hat{i} -3 \hat{j} +5 \hat{k})$

Solution

The equations of the given planes are $\vec{r} \cdot(2 \hat{i}+2 \hat{j}-3 \hat{k})=5$ and $\vec{r} \cdot(3 \hat{i}-3 \hat{j}+5 \hat{k})=3$

It is known that if $ \vec{n} _1$ and $ \vec{n} _2$ are normal to the planes, $\vec{r} \cdot \vec{n} _1=d_1$ and $\vec{r} \cdot \vec{n} _2=d_2$, then the angle between them, $Q$, is given by,

$\cos Q=|\frac{ \vec{n} _1 \cdot \vec{n} _2}{| \vec{n} _1|| \vec{n} _2|}|$

Here, $ \vec{n} _1=2 \hat{i}+2 \hat{j}-3 \hat{k}$ and $ \vec{n} _2=3 \hat{i}-3 \hat{j}+5 \hat{k}$

$\therefore \vec{n} _1 \cdot \vec{n} _2=(2 \hat{i}+2 \hat{j}-3 \hat{k})(3 \hat{i}-3 \hat{j}+5 \hat{k})=2.3+2 \cdot(-3)+(-3) \cdot 5=-15$

$| \vec{n} _1|=\sqrt{(2)^{2}+(2)^{2}+(-3)^{2}}=\sqrt{17}$

$| \vec{n} _2|=\sqrt{(3)^{2}+(-3)^{2}+(5)^{2}}=\sqrt{43}$

Substituting the value of $\vec{n} \cdot \vec{n} _2,| \vec{n} _1|$ and $| \vec{n} _2|$ in equation (1), we obtain

$\cos Q=|\frac{-15}{\sqrt{17} \cdot \sqrt{43}}|$

$\Rightarrow \cos Q=\frac{15}{\sqrt{731}}$

$\Rightarrow \cos Q^{-1}=(\frac{15}{\sqrt{731}})$

13. In the following cases, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles bet ween them.

(a) $7 x+5 y+6 z+30=0$ and $3 x$ - $y $ - $10 z+4=0$

(b) $2 x+y+3 z - 2=0$ and $x - 2 y+5=0$

(c) $2 x$ - $2 y+4 z+5=0$ and $3 x - 3 y+6 z - 1=0$

(d) $2 x - y+3 z - 1=0$ and $2 x - y+3 z+3=0$

(e) $4 x+8 y+z - 8=0$ and $y+z - 4=0$

Solution

The direction ratios of normal to the plane, $L_1: a_1 x+b_1 y+c_1 z=0$, are $a_1, b_1, c_1$ and $L_2: a_1 x+b_2 y+c_2 z=0$ are $a_2, b_2, c_2$.

$L_1 | L_2$, if $\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}$

$L_1 \perp L_2$, if $a_1 a_2+b_1 b_2+c_1 c_2=0$

The angle between $L_1$ and $L_2$ is given by,

$Q=\cos ^{-1}|\frac{a_1 a_2+b_1 b_2+c_1 c_2}{\sqrt{a_1^{2}+b_1^{2}+c_1^{2} \cdot \sqrt{a_2^{2}+b_2^{2}+c_2^{2}}}}|$

(a) The equations of the planes are $7 x+5 y+6 z+30=0$ and

$3 x-y-10 z+4=0$

Here, $a_1=7, b_1=5, c_1=6$ $a_2=3, b_2=-1, c_2=-10$

$a_1 a_2+b_1 b_2+c_1 c_2=7 \times 3+5 \times(-1)+6 \times(-10)=-44 \neq 0$

Therefore, the given planes are not perpendicular.

$\frac{a_1}{a_2}=\frac{7}{3}, \frac{b_1}{b_2}=\frac{5}{-1}=-5, \frac{c_1}{c_2}=\frac{6}{-10}=\frac{-3}{5}$

It can be seen that, $\frac{a_1}{a_2} \neq \frac{b_1}{b_2} \neq, \frac{c_1}{c_2}$

Therefore, the given planes are not parallel.

The angle between them is given by,

$ \begin{aligned} Q & =\cos ^{-1}|\frac{7 \times 3+5 \times(-1)+6 \times(-10)}{\sqrt{(7)^{2}+(5)^{2}+(6)^{2}} \times \sqrt{(3)^{2}+(-1)^{2}+(-10)^{2}}}| \\ & =\cos ^{-1}|\frac{21-5-60}{\sqrt{110} \times \sqrt{110}}| \\ & =\cos ^{-1} \frac{44}{110} \\ & =\cos ^{-1} \frac{2}{5} \end{aligned} $

(b) The equations of the planes are $2 x+y+3 z-2=0$ and $x-2 y+5=0$

Here, $a_1=2, b_1=1, c_1=3$ and $a_2=1, b_2=-2, c_2=0$

$\therefore a_1 a_2+b_1 b_2+c_1 c_2=2 \times 1+1 \times(-2)+3 \times 0=0$

Thus, the given planes are perpendicular to each other.

(c) The equations of the given planes are $2 x-2 y+4 z+5=0$ and $3 x-3 y+6 z-1=0$

Here, $a_1=2, b_1-2, c_1=4$ and

$a_2=3, b_2=-3, c_2=6 \quad a_1 a_2+b_1 b_2+c_1 c_2=2 \times 3+(-2)(-3)+4 \times 6=6+6+24=36 \neq 0$

Thus, the given planes are not perpendicular to each other.

$\frac{a_1}{a_2}=\frac{2}{3}, \frac{b_1}{b_2}=\frac{-2}{-3}=\frac{2}{3}$ and $\frac{c_1}{c_2}=\frac{4}{6}=\frac{2}{3}$ $\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}$

Thus, the given planes are parallel to each other.

(d) The equations of the planes are $2 x-y+3 z-1=0$ and $2 x-y+3 z+3=0$

Here, $a_1=2, b_1=-1, c_1=3$ and $a_2=2, b_2=-1, c_2=3$

$\frac{a_1}{a_2}=\frac{2}{2}=1, \frac{b_1}{b_2}=\frac{-1}{-1}=1$ and $\frac{c_1}{c_2}=\frac{3}{3}=1$

$\therefore \frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}$

Thus, the given lines are parallel to each other.

(e) The equations of the given planes are $4 x+8 y+z-8=0$ and $y+z-4=0$

Here, $a_1=4, b_1=8, c_1=1$ and $a_2=0, b_2=1, c_2=1$

$a_1 a_2+b_1 b_2+c_1 c_2=4 \times 0+8 \times 1+1=9 \neq 0$

Therefore, the given lines are not perpendicular to each other.

$\frac{a_1}{a_2}=\frac{4}{0}, \frac{b_1}{b_2}=\frac{8}{1}=8, \frac{c_1}{c_2}=\frac{1}{1}=1$

$\therefore \frac{a_1}{a_2} \neq \frac{b_1}{b_2} \neq, \frac{c_1}{c_2}$

Therefore, the given lines are not parallel to each other.

The angle between the planes is given by,

$Q=\cos ^{-1}|\frac{4 \times 0+8 \times 1+1 \times 1}{\sqrt{4^{2}+8^{2}+1^{2}} \times \sqrt{0^{2}+1^{2}+1^{2}}}|=\cos ^{-1}|\frac{9}{9 \times \sqrt{2}}|=\cos ^{-1}(\frac{1}{\sqrt{2}})=45^{\circ}$

14. In the following cases, find the distance of each of the given points from the corresponding given plane.

Point

(a) $(0,0,0)$

(b) (3,-2,1)

(c) (2,3, -5)

(d) (-6,0,0)

Plane

$3 x - 4 y+12 z=3$

$2 x$ - $y+2 z+3=0$

$x+2 y$ - $2 z=9$

$2 x - 3 y+6 z - 2=0$

Solution

It is known that the distance between a point, $p(x_1, y_1, z_1)$, and a plane, $A x+B y+C z=$ $D$, is given by,

$d=|\frac{A x_1+B y_1+C z_1-D}{\sqrt{A^{2}+B^{2}+C^{2}}}|$

(a) The given point is $(0,0,0)$ and the plane is $3 x-4 y+12 z=3$

$\therefore d=|\frac{3 \times 0-4 \times 0+12 \times 0-3}{\sqrt{(3)^{2}+(-4)^{2}+(12)^{2}}}|=\frac{3}{\sqrt{169}}=\frac{3}{13}$

(b) The given point is $(3,-2,1)$ and the plane is $2 x-y+2 z+3=0$

$\therefore=|\frac{2 \times 3-(-2)+2 \times 1+3}{\sqrt{(2)^{2}+(-1)^{2}+(2)^{2}}}|=|\frac{13}{3}|=\frac{13}{3}$

(c) The given point is $(2,3,-5)$ and the plane is $x+2 y-2 z=9$

$\therefore d=|\frac{2+2 \times 3-2(-5)-9}{\sqrt{(1)^{2}+(2)^{2}+(-2)^{2}}}|=\frac{9}{3}=3$

(d) The given point is $(-6,0,0)$ and the plane is $2 x-3 y+6 z-2=0$

$ d=|\frac{2(-6)-3 \times 0+6 \times 0-2}{\sqrt{(2)^{2}+(-3)^{2}+(6)^{2}}}|=|\frac{-14}{\sqrt{49}}|=\frac{14}{7}=2 $

Miscellaneous Examples

Example $26 \mathrm{~A}$ line makes angles $\alpha, \beta, \gamma$ and $\delta$ with the diagonals of a cube, prove that

$$ \cos ^{2} \alpha+\cos ^{2} \beta+\cos ^{2} \gamma+\cos ^{2} \delta=\frac{4}{3} $$

Solu tion A cube is a rectangular parallelopipedhavingequal length, breadth and height.

Let OADBFEGC be the cube with each side of length $a$ units. (Fig11.21)

The four diagonals are OE, AF, BG and CD.

The direction cosines of the diagonal $\mathrm{OE}$ which is the line joining two points $\mathrm{O}$ andE are

$$ \frac{a-0}{\sqrt{a^{2}+a^{2}+a^{2}}}, \frac{a-0}{\sqrt{a^{2}+a^{2}+a^{2}}}, \frac{a-0}{\sqrt{a^{2}+a^{2}+a^{2}}} $$

i.e., $\quad \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}$

Fig 11.21

Similarly, the direction cosines of AF, BG and CD are $\frac{\mathrm{i} 1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}} ; \frac{1}{\sqrt{3}}$, $\frac{- 1}{\sqrt{3}}, \frac{1}{\sqrt{3}}$ and $\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{- 1}{\sqrt{3}}$, respectively.

Let $l, m, n$ be the direction cosines of the given line which makes angles $\alpha, \beta, \gamma, \delta$ with OE, AF, BG CD, respectively. Then

$$ \begin{aligned} & \cos \alpha=\frac{1}{\sqrt{3}}(l+m+n) ; \cos \beta=\frac{1}{\sqrt{3}}(- l+m+n) \ & \cos \gamma=\frac{1}{\sqrt{3}}(l - m+n) ; \cos \delta=\frac{1}{\sqrt{3}}(l+m - n) \quad \text { (Why?) } \end{aligned} $$

Squaring and adding, we get

$$ \begin{aligned} \cos ^{2} \alpha & +\cos ^{2} \beta+\cos ^{2} \gamma+\cos ^{2} \delta \ & \left.=\frac{1}{3}\left[(l+m+n)^{2}+(- l+m+n)^{2}\right]+(l - m+n)^{2}+(l+m - n)^{2}\right] \ & =\frac{1}{3}\left[4\left(l^{2}+m^{2}+n^{2}\right)\right]=\frac{4}{3} \quad\left(\text { as } l^{2}+m^{2}+n^{2}=1\right) \end{aligned} $$

Example 27 Find the equation of the plane that contains the point $(1, - 1,2)$ and is perpendicular to each of the planes $2 x+3 y - 2 z=5$ and $x+2 y - 3 z=8$.

Solution The equation of the plane containing the given point is

$$ \begin{equation*} \mathrm{A}(x - 1)+\mathrm{B}(y+1)+\mathrm{C}(z - 2)=0 \tag{1} \end{equation*} $$

Applying the condition of perpendicularly to the plane given in (1) with the planes

$$ \begin{aligned} & 2 x+3 y - 2 z=5 \text { and } x+2 y 3 z=8 \text {, we have } \ & 2 \mathrm{~A}+3 \mathrm{~B} \text { - } 2 \mathrm{C}=0 \text { and } \mathrm{A}+2 \mathrm{~B} \text { - } 3 \mathrm{C}=0 \end{aligned} $$

Solving these equations, we find $A=- \quad 5 C$ and $B=4 C$. Hence, the required equation is

• 5 C(x - 1)+4 C(y+1)+C(z - 2)=0

i.e.

$$ 5 x - 4 y - z=7 $$

Example 28 Find the distance between the point $\mathrm{P}(6,5,9)$ andthe plane determined by the points $\mathrm{A}(3, - 1,2), \mathrm{B}(5,2,4)$ and $C(- 1, \mathrm{i} ~ 1,6)$.

Solution Let A, B, Cbethethree pointsintheplane. Disthefoot of the perpendicular drawn from a point $\mathrm{P}$ to the plane. $\mathrm{PD}$ is the requireddistance to be determined, which is the projection of $\overrightarrow{\mathrm{AP}}$ on $\overrightarrow{\mathrm{AB}} \times \overrightarrow{\mathrm{AC}}$.

Hence, $\mathrm{PD}=$ the dot product of $\overrightarrow{\mathrm{AP}}$ with the unit vector along $\overrightarrow{\mathrm{AB}} \times \overrightarrow{\mathrm{AC}}$.

So

$$ \overrightarrow{\mathrm{AP}}=3 \hat{\hat{i}}+6 \hat{j}+7 \hat{\hat{k}} $$

and

$$ \overrightarrow{\mathrm{AB}} \times \overrightarrow{\mathrm{AC}}=\left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k} \\ 2 & 3 & 2 \\ -4 & 0 & 4 \end{array}\right|=12 \hat{\hat{i}}-16 \hat{j}+12 \check{\hat{k}} $$

Unit vector along $\overrightarrow{\mathrm{AB}} \times \overrightarrow{\mathrm{AC}}=\frac{3 \hat{E}_{-} 4 \hat{\hat{j}^{2}}+3 \hat{\hat{E}^{2}}}{\sqrt{34}}$

Hence

$$ \begin{aligned} & P D=\left(3 \hat{i} 6 \hat{j}_{+} 7 \hat{j}\right) \cdot \frac{3 \hat{E}-4 \hat{E}+3 \hat{k}}{\sqrt{34}} \\ & =\frac{3 \sqrt{34}}{17} \end{aligned} $$

Alternatively, find the equation of the plane passing through A, B and C and then computethedistance of the point $\mathrm{P}$ from theplane.

Example 29 Showthat the lines

$$ \frac{x-a+d}{\alpha-\delta}=\frac{y-a}{\alpha}=\frac{z-a-d}{\alpha+\delta} $$

and

$$ \frac{x-b+c}{\beta-\gamma}=\frac{y-b}{\beta}=\frac{z-b-c}{\beta+\gamma} \text { are coplanar. } $$

Solution

Here

$$ \begin{array}{ll} x_{1}=a - d & x_{2}=b - c \\ y_{1}=a & y_{2}=b \\ z_{1}=a+d & z_{2}=b+c \\ a_{1}=\alpha - \delta & a_{2}=\beta \ddot{\mathrm{i} \gamma} \\ b_{1}=\alpha & b_{2}=\beta \\ c_{1}=\alpha+\delta & c_{2}=\beta+\gamma \end{array} $$

Nowconsider the determinant

$$ \left|\begin{array}{ccc} x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\ a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \end{array}\right|=\left|\begin{array}{ccc} b-c-a+d & b-a & b+c-a-d \\ \alpha-\delta & \alpha & \alpha+\delta \\ \beta-\gamma & \beta & \beta+\gamma \end{array}\right| $$

Adding third column to the first column, we get

$$ 2\left|\begin{array}{ccc} b-a & b-a & b+c-a-d \\ \alpha & \alpha & \alpha+\delta \\ \beta & \beta & \beta+\gamma \end{array}\right|=0 $$

Since the first and second columns are identical. Hence, the given two lines are coplanar.

Example 30 Find the coordinates of the point where the line through the points A $(3,4,1)$ and $B(5,1,6)$ crosses the $X Y$-plane.

Solution Thevector equation of the line through thepoints $A$ and Bis

$$ \vec{r}=3 \hat{i}+4 \hat{j}+\hat{k}+\lambda[(5-3) \hat{i}+(1-4) \hat{j}+(6-1) \hat{k}] $$ i.e. $$\quad \vec{r}=3 \hat{i}+4 \hat{j}+\hat{k}+\lambda(2 \hat{i}-3 \hat{j}+5 \hat{k})$$

Let $\mathrm{P}$ be the point where the line $\mathrm{AB}$ crosses the $\mathrm{XY}$-plane. Then the position vector of the point $\mathrm{P}$ is of the form $x \hat{\hat{i}}_{+} y \hat{j}$.

This point must satisfy the equation (1). (Why ?)

i.e. $\quad x \hat{i} + k \hat{j}=(3+2 \lambda) \hat{i}+(4-3 \lambda) \hat{j}+(1+5 \lambda) \hat{k}$

Equating the likecoefficients of $\hat{j}, \hat{j}$ and $\hat{E}$, wehave

$$ \begin{aligned} & x=3+2 \lambda \ & y=4 \text { - } 3 \lambda \ & 0=1+5 \lambda \end{aligned} $$

Solving the above equations, we get

$$ x=\frac{13}{5} \text { and } y=\frac{23}{5} $$

Hence, the coordinates of the required point are $\left(\frac{13}{5}, \frac{23}{5}, 0\right)$.

Miscellaneous Exercise on Chapter 11

1. Find the angle between the lines whose direction ratios are $a, b, c$ and $b-c, c-a, a-b$.

Solution

The angle $Q$ between the lines with direction cosines, $a, b, c$ and $b-c, c-a$, $a-b$, is given by,

$\cos Q=|\frac{a(b-c)+b(c-a)+c(a-b)}{\sqrt{a^{2}+b^{2}+c^{2}}+\sqrt{(b-c)^{2}+(c-a)^{2}+(a-b)^{2}}}|$

$\Rightarrow \cos Q=0$

$\Rightarrow Q=\cos ^{-1} 0$

$\Rightarrow Q=90^{\circ}$

Thus, the angle between the lines is $90^{\circ}$.

2. Find the equation of a line parallel to $x$-axis and passing through the origin.

Solution

The line parallel to $x$-axis and passing through the origin is $x$-axis itself.

Let $A$ be a point on $x$-axis. Therefore, the coordinates of $A$ are given by $(a, 0,0)$, where

$a \in R$.

Direction ratios of $OA$ are $(a-0)=a, 0,0$

The equation of $O A$ is given by,

$\frac{x-0}{a}=\frac{y-0}{0}=\frac{z-0}{0}$

$\Rightarrow \frac{x}{1}=\frac{y}{0}=\frac{z}{0}=a$

Thus, the equation of line parallel to $x$-axis and passing through origin is $\frac{x}{1}=\frac{y}{0}=\frac{z}{0}$

3. If the lines $\frac{x-1}{-3}=\frac{y-2}{2 k}=\frac{z-3}{2}$ and $\frac{x-1}{3 k}=\frac{y-1}{1}=\frac{z-6}{-5}$ are perpendicular, find the value of $k$.

Solution

The direction of ratios of the lines, $\frac{x-1}{-3}=\frac{y-2}{2 k}=\frac{z-3}{2}$ and $\frac{x-1}{3 k}=\frac{y-1}{1}=\frac{z-6}{-5}$, are -3 , $2 k, 2$ and $3 k, 1,-5$ respectively.

It is known that two lines with direction ratios, $a_1, b_1, c_1$ and $a_2, b_2, c_2$, are perpendicular, if $a_1 a_2+b_1 b_2+c_1 c_2=0$

$\therefore-3(3 k)+2 k \times 1+2(-5)=0$

$\Rightarrow-9 k+2 k-10=0$

$\Rightarrow 7 k=-10$

$\Rightarrow k=\frac{-10}{7}$

Therefore, for $k=-\frac{10}{7}$, the given lines are perpendicular to each other.

4. Find the shortest distance between lines $\vec{r}=6 \hat{i}+2 \hat{j}+2 \hat{k}+\lambda(\hat{i}-2 \hat{j}+2 \hat{k})$ and $\vec{r}=-4 \hat{i}-\hat{k}+\mu(3 \hat{i}-2 \hat{j}-2 \hat{k})$.

Solution

The given lines are

$\vec{r}=6 \hat{i}+2 \hat{j}+2 \hat{k}+\lambda(\hat{i}-2 \hat{j}+2 \hat{k})$

$\vec{r}=-4 \hat{i}-\hat{k}+\mu(3 \hat{i}-2 \hat{j}-2 \hat{k})$

It is known that the shortest distance between two lines, $\vec{r}= \vec{a} _1+\lambda \vec{b} _1$ and $\vec{r}= \vec{a} _2+\lambda \vec{b} _2$, is given by

$d=|\frac{( \vec{b} _1 \times \vec{b} _2) \cdot( \vec{a} _2- \vec{a} _1)}{| \vec{b} _1 \times \vec{b} _2|}|$

Comparing $\vec{r}= \vec{a} _1+\lambda \vec{b} _1$ and $\vec{r}= \vec{a} _2+\lambda \vec{b} _2$ to equations (1) and (2), we obtain

$ \vec{a} _1=6 \hat{i}+2 \hat{j}+2 \hat{k}$

$ \vec{b} _1=\hat{i}-2 \hat{j}+2 \hat{k}$

$ \vec{a} _2=-4 \hat{i}-\hat{k}$

$ \vec{b} _2=3 \hat{i}-2 \hat{j}-2 \hat{k}$

$\Rightarrow \vec{a} _2- \vec{a} _1=(-4 \hat{i}-\hat{k})-(6 \hat{i}+2 \hat{j}+2 \hat{k})=-10 \hat{i}-2 \hat{j}-3 \hat{k}$

$ \begin{aligned} & \Rightarrow \vec{b} _1 \times \vec{b} _2= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & -2 & 2 \\ 3 & -2 & -2 \end{vmatrix} =(4+4) \hat{i}-(-2-6) \hat{j}+(-2+6) \hat{k}=8 \hat{i}+8 \hat{j}+4 \hat{k} \\ & \therefore| \vec{b} _1 \times \vec{b} _2|=\sqrt{(8)^{2}+(8)^{2}+(4)^{2}}=12 \end{aligned} $

$ ( \vec{b} _1 \times \vec{b} _2) \cdot( \vec{a} _2- \vec{a} _1)=(8 \hat{i}+8 \hat{j}+4 \hat{k}) \cdot(-10 \hat{i}-2 \hat{j}-3 \hat{k})=-80-16-12=-108 $

Substituting all the values in equation (1), we obtain

$d=|\frac{-108}{12}|=9$

Therefore, the shortest distance between the two given lines is 9 units.

5. Find the vector equation of the line passing through the point $(1,2,-4)$ and perpendicular to the two lines:

$\quad\quad$ $ \frac{x-8}{3}=\frac{y+19}{-16}=\frac{z-10}{7} \text{ and } \frac{x-15}{3}=\frac{y-29}{8}=\frac{z-5}{-5} . $

Solution

Let the required line be parallel to vector $\vec{b}$ given by,

$\vec{b}=b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}$

The position vector of the point $(1,2,3)$ is $\vec{a}=\hat{i}+2 \hat{j}+3 \hat{k}$

The equation of line passing through $(1,2,3)$ and parallel to $\vec{b}$ is given by,

$$ \begin{align*} & \vec{r}=\vec{a}+\lambda \vec{b} \\ & \Rightarrow \vec{r}(\hat{i}+2 \hat{j}+3 \hat{k})+\lambda(b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}) \tag{1} \end{align*} $$

The equations of the given planes are $\vec{r} \cdot(\hat{i}-\hat{j}+2 \hat{k})=5$

$\vec{r} \cdot(3 \hat{i}+\hat{j}+\hat{k})=6$

The line in equation (1) and plane in equation (2) are parallel. Therefore, the normal to the plane of equation (2) and the given line are perpendicular.

$\Rightarrow(\hat{i}-\hat{j}+2 \hat{k}) \cdot \lambda(b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k})=0$

$\Rightarrow \lambda(b_1-b_2+2 b_3)=0$

$\Rightarrow b_1-b_2+2 b_3=0$

Similarly, $(3 \hat{i}+\hat{j}+\hat{k}) \cdot \lambda(b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k})=0$

$\Rightarrow \lambda(3 b_1+b_2+b_3)=0$

$\Rightarrow 3 b_1+b_2+b_3=0$

From equations (4) and (5), we obtain

$\frac{b_1}{(-1) \times 1-1 \times 2}=\frac{b_2}{2 \times 3-1 \times 1}=\frac{b_3}{1 \times 1-3(-1)}$

$\Rightarrow \frac{b_1}{-3}=\frac{b_2}{5}=\frac{b_3}{4}$

Therefore, the direction ratios of $\vec{b}$ are $-3,5$, and 4 .

$\therefore \vec{b}=b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}=-3 \hat{i}+5 \hat{j}+4 \hat{k}$

Substituting the value of $\vec{b}$ in equation (1), we obtain

$\vec{r}=(\hat{i}+2 \hat{j}+3 \hat{k})+\lambda(-3 \hat{i}+5 \hat{j}+4 \hat{k})$

This is the equation of the required line.

Summary

Direction cosines of a line are the cosines of the angles made by the line with the positive directions of the coordinate axes.

If $l, m, n$ are the direction cosines of a line, then $l^{2}+m^{2}+n^{2}=1$.

Direction cosines of a line joining two points $P(x_1, y_1, z_1)$ and $Q(x_2, y_2, z_2)$ are

$ \frac{x_2-x_1}{PQ}, \frac{y_2-y_1}{PQ}, \frac{z_2-z_1}{PQ} $

where $PQ=\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}+(z_2-z_1)^{2}}$

$\Delta$ Direction ratios of a line are the numbers which are proportional to the direction cosines of a line.

• If $l, m, n$ are the direction cosines and $a, b, c$ are the direction ratios of a line then

$ l=\frac{a}{\sqrt{a^{2}+b^{2}+c^{2}}} ; m=\frac{b}{\sqrt{a^{2}+b^{2}+c^{2}}} ; n=\frac{c}{\sqrt{a^{2}+b^{2}+c^{2}}} $

Skew lines are lines in space which are neither parallel nor intersecting. They lie in different planes.

• Angle between skew lines is the angle between two intersecting lines drawn from any point (preferably through the origin) parallel to each of the skew lines.
• If $l_1, m_1, n_1$ and $l_2, m_2, n_2$ are the direction cosines of two lines; and $\theta$ is the acute angle between the two lines; then

$ \cos \theta=|l_1 l_2+m_1 m_2+n_1 n_2| $

If $a_1, b_1, c_1$ and $a_2, b_2, c_2$ are the direction ratios of two lines and $\theta$ is the acute angle between the two lines; then

$ \cos \theta=|\frac{a_1 a_2+b_1 b_2+c_1 c_2}{\sqrt{a_1^{2}+b_1^{2}+c_1^{2}} \sqrt{a_2^{2}+b_2^{2}+c_2^{2}}}| $

Vector equation of a line that passes through the given point whose position vector is $\vec{a}$ and parallel to a given vector $\vec{b}$ is $\vec{r}=\vec{a}+\lambda \vec{b}$.

Equation of a line through a point $(x_1, y_1, z_1)$ and having direction cosines $l, m, n$ is

$ \frac{x-x_1}{l}=\frac{y-y_1}{m}=\frac{z-z_1}{n} $

• The vector equation of a line which passes through two points whose position vectors are $\vec{a}$ and $\vec{b}$ is $\vec{r}=\vec{a}+\lambda(\vec{b}-\vec{a})$.

$\Delta$ If $\theta$ is the acute angle between $\vec{r}= \vec{a} _ {1}+\lambda \vec{b} _ {1}$ and $\vec{r}= \vec{a} _ {2}+\lambda \vec{b} _ {2}$, then $\cos \theta=|\frac{ \vec{b} _ {1} \cdot \vec{b} _ {2}}{| \vec{b} _ {1}|| \vec{b} _ {2}|}|$

$\checkmark$ If $\frac{x-x_1}{l_1}=\frac{y-y_1}{m_1}=\frac{z-z_1}{n_1}$ and $\frac{x-x_2}{l_2}=\frac{y-y_2}{m_2}=\frac{z-z_2}{n_2}$

are the equations of two lines, then the acute angle between the two lines is given by $\cos \theta=|l_1 l_2+m_1 m_2+n_1 n_2|$.

• Shortest distance between two skew lines is the line segment perpendicular to both the lines.

Shortest distance between $\vec{r}= \vec{a} _ {1}+\lambda \vec{b} _ {1}$ and $\vec{r}= \vec{a} _ {2}+\mu \vec{b} _ {2}$ is

$ |\frac{( \vec{b} _ {1} \times \vec{b} _ {2}) \cdot( \vec{a} _ {2}- \vec{a} _ {1})}{| \vec{b} _ {1} \times \vec{b} _ {2}|}| $

Shortest distance between the lines: $\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1}$ and

$ \frac{x-x_2}{a_2}=\frac{y-y_2}{b_2}=\frac{z-z_2}{c_2} \text{ is } $

$ \frac{ \begin{vmatrix} x_2-x_1 & y_2-y_1 & z_2-z_1 \\ a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \end{vmatrix} }{\sqrt{(b_1 c_2-b_2 c_1)^{2}+(c_1 a_2-c_2 a_1)^{2}+(a_1 b_2-a_2 b_1)^{2}}} $

Distance between parallel lines $\vec{r}= \vec{a} _ {1}+\lambda \vec{b}$ and $\vec{r}= \vec{a} _ {2}+\mu \vec{b}$ is

$|\frac{\vec{b} \times( \vec{a} _ {2}- \vec{a} _ {1})}{|\vec{b}|}|$