Mathematics 11
- Chapter 1 Sets
- Chapter 2 Relations And Functions
- Chapter 3 Trigonometric Functions
- Chapter 4 Complex numbers and quadratic equations
- Chapter 5 Linear Inequalities
- Chapter 6 Permutations And Combinations
- Chapter 7 Binomial Theorem
- Chapter 8 Sequences And Series
- Chapter 9 Straight Lines
- Chapter 10 Conic Sections
- Chapter 11 Introduction To Three Dimensional Geometry
- Chapter 12 Limits And Derivaties
- Chapter 13 Statistics
- Chapter 14 Probability
Chapter 9 Straight Lines
STRAIGHT LINES
Geometry, as a logical system, is a means and even the most powerful means to make children feel the strength of the human spirit that is of their own spirit. - H. FREUDENTHAL
9.1 Introduction
We are familiar with two-dimensional coordinate geometry from earlier classes. Mainly, it is a combination of algebra and geometry. A systematic study of geometry by the use of algebra was first carried out by celebrated French philosopher and mathematician René Descartes, in his book ‘La Géométry, published in 1637. This book introduced the notion of the equation of a curve and related analytical methods into the study of geometry. The resulting combination of analysis and geometry is referred now as analytical geometry. In the earlier classes, we initiated the study of coordinate geometry, where we studied about coordinate axes, coordinate plane, plotting of points in a
 plane, distance between two points, section formulae, etc. All these concepts are the basics of coordinate geometry.
plane, distance between two points, section formulae, etc. All these concepts are the basics of coordinate geometry.
Let us have a brief recall of coordinate geometry done in earlier classes. To recapitulate, the location of the points $(6,-4)$ and $(3,0)$ in the XY-plane is shown in Fig 9.1.

We may note that the point $(6,-4)$ is at 6 units distance from the $y$-axis measured along the positive $x$-axis and at 4 units distance from the $x$-axis measured along the negative $y$-axis. Similarly, the point $(3,0)$ is at 3 units distance from the $y$-axis measured along the positive $x$-axis and has zero distance from the $x$-axis. formulae:
We also studied there following important
I. Distance between the points $P(x_1, y_1)$ and $Q(x_2, y_2)$ is
$ PQ=\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}} $
For example, distance between the points $(6,-4)$ and $(3,0)$ is
$ \sqrt{(3-6)^{2}+(0+4)^{2}}=\sqrt{9+16}=5 \text{ units. } $
II. The coordinates of a point dividing the line segment joining the points $(x_1, y_1)$ and $(x_2, y_2)$ internally, in the ratio $m: n$ are $(\frac{m x_2+n x_1}{m+n}, \frac{m y_2+n y_1}{m+n})$.
For example, the coordinates of the point which divides the line segment joining
A $(1,-3)$ and $B(-3,9)$ internally, in the ratio $1: 3$ are given by $x=\frac{1 .(-3)+3.1}{1+3}=0$
$ \text{ and } y=\frac{1.9+3 \cdot(-3)}{1+3}=0 $
III. In particular, if $m=n$, the coordinates of the mid-point of the line segment joining the points $(x_1, y_1)$ and $(x_2, y_2)$ are $(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2})$.
IV. Area of the triangle whose vertices are $(x _{1,} y_1),(x_2, y_2)$ and $(x_3, y_3)$ is
$ \frac{1}{2}|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)| . $
For example, the area of the triangle, whose vertices are $(4,4),(3,-2)$ and $(-3,16)$ is
$ \frac{1}{2}|4(-2-16)+3(16-4)+(-3)(4+2)|=\frac{|-54|}{2}=27 $
Remark If the area of the triangle $ABC$ is zero, then three points $A, B$ and $C$ lie on a line, i.e., they are collinear.
In the this Chapter, we shall continue the study of coordinate geometry to study properties of the simplest geometric figure - straight line. Despite its simplicity, the line is a vital concept of geometry and enters into our daily experiences in numerous interesting and useful ways. Main focus is on representing the line algebraically, for which slope is most essential.
9.2 Slope of a Line
A line in a coordinate plane forms two angles with the $x$-axis, which are supplementary.
The angle (say) $\theta$ made by the line $l$ with positive direction of $x$-axis and measured anti clockwise is called the inclination of the line. Obviously $0^{\circ} \leq \theta \leq 180^{\circ}$ (Fig 9.2).

We observe that lines parallel to $x$-axis, or coinciding with $x$-axis, have inclination of $0^{\circ}$. The inclination of a vertical line (parallel to or coinciding with $y$-axis) is $90^{\circ}$.
Definition 1 If $\theta$ is the inclination of a line $l$, then $\tan \theta$ is called the slope or gradient of the line $l$.
The slope of a line whose inclination is $90^{\circ}$ is not defined.
The slope of a line is denoted by $m$.
Thus, $m=\tan \theta, \theta \neq 90^{\circ}$
It may be observed that the slope of $x$-axis is zero and slope of $y$-axis is not defined.
9.2.1 Slope of a line when coordinates of any two points on the line are given
We know that a line is completely determined when we are given two points on it. Hence, we proceed to find the slope of a line in terms of the coordinates of two points on the line.
Let $P(x_1, y_1)$ and $Q(x_2, y_2)$ be two points on non-vertical line $l$ whose inclination is $\theta$. Obviously, $x_1 \neq x_2$, otherwise the line will become perpendicular to $x$-axis and its slope will not be defined. The inclination of the line $l$ may be acute or obtuse. Let us take these two cases.
Draw perpendicular $QR$ to $x$-axis and $PM$ perpendicular to $RQ$ as shown in Figs. 9.3 (i) and (ii).
Case 1 When angle $\theta$ is acute:

In Fig 9.3 (i), $\angle MPQ=\theta \quad \quad \quad \quad \quad \quad \ldots (1)$
Therefore, slope of line $l=m=\tan \theta$.
But in $\triangle MPQ$, we have $\tan \theta=\frac{MQ}{MP}=\frac{y_2-y_1}{x_2-x_1} \quad \quad \quad \quad \quad \quad \ldots (2)$
From equations (1) and (2), we have
$ m=\frac{y_2-y_1}{x_2-x_1} $
Case II When angle $\theta$ is obtuse:

In Fig 9.3 (ii), we have
$\angle MPQ=180^{\circ}-\theta$.
Therefore, $\theta=180^{\circ}-\angle MPQ$.
Now, slope of the line $l$
$ \begin{aligned} m & =\tan \theta \\ & =\tan (180^{\circ}-\angle MPQ)=-\tan \angle MPQ \\ & =-\frac{MQ}{MP}=-\frac{y_2-y_1}{x_1-x_2}=\frac{y_2-y_1}{x_2-x_1} . \end{aligned} $
Consequently, we see that in both the cases the slope $m$ of the line through the points $(x_1, y_1)$ and $(x_2, y_2)$ is given by $m=\frac{y_2-y_1}{x_2-x_1}$.
9.2.2 Conditions for parallelism and perpendicularity of lines in terms of their
slopes In a coordinate plane, suppose that non-vertical lines $l_1$ and $l_2$ have slopes $m_1$ and $m_2$, respectively. Let their inclinations be $\alpha$ and $\beta$, respectively.If the line $\boldsymbol{l_1}$ is parallel to $\boldsymbol{l_2}$ (Fig 9.4), then their inclinations are equal, i.e.,

$ \alpha=\beta, \text{ and hence, } \tan \alpha=\tan \beta $
Therefore $m_1=m_2$, i.e., their slopes are equal.
Conversely, if the slope of two lines $l_1$ and $l_2$ is same, i.e.,
Then
$ m_1=m_2 $
$ \tan \alpha=\tan \beta \text{. } $
By the property of tangent function (between $0^{\circ}$ and $180^{\circ}$ ), $\alpha=\beta$.
Therefore, the lines are parallel.
Hence, two non vertical lines $l_1$ and $l_2$ are parallel if and only if their slopes are equal.
If the lines $ \boldsymbol{l_1 } $ and $\boldsymbol{l_2 } $ are perpendicular (Fig 9.5), then $\beta=\alpha+90^{\circ}$.

Therefore, $\tan \beta=\tan (\alpha+90^{\circ})$
$ =-\cot \alpha=-\frac{1}{\tan \alpha} $
i.e., $\quad m_2=-\frac{1}{m_1}$ or $\quad m_1 m_2=-1$
Conversely, if $m_1 m_2=-1$, i.e., $\tan \alpha \tan \beta=-1$.
Then $\tan \alpha=-\cot \beta=\tan (\beta+90^{\circ})$ or $\tan (\beta-90^{\circ})$
Therefore, $\alpha$ and $\beta$ differ by $90^{\circ}$.
Thus, lines $l_1$ and $l_2$ are perpendicular to each other.
Hence, two non-vertical lines are perpendicular to each other if and only if their slopes are negative reciprocals of each other,
i.e., $\quad m_2=-\frac{1}{m_1}$ or, $m_1 m_2=-1$.
Let us consider the following example.
Example 1 Find the slope of the lines:
(a) Passing through the points $(3,-2)$ and $(-1,4)$,
(b) Passing through the points $(3,-2)$ and $(7,-2)$,
(c) Passing through the points $(3,-2)$ and $(3,4)$,
(d) Making inclination of $60^{\circ}$ with the positive direction of $x$-axis.
Solution (a) The slope of the line through $(3,-2)$ and $(-1,4)$ is
$ m=\frac{4-(-2)}{-1-3}=\frac{6}{-4}=-\frac{3}{2} $
(b) The slope of the line through the points $(3,-2)$ and $(7,-2)$ is
$ m=\frac{-2-(-2)}{7-3}=\frac{0}{4}=0 $
(c) The slope of the line through the points $(3,-2)$ and $(3,4)$ is
$ m=\frac{4-(-2)}{3-3}=\frac{6}{0} \text{, which is not defined. } $
(d) Here inclination of the line $\alpha=60^{\circ}$. Therefore, slope of the line is
$ m=\tan 60^{\circ}=\sqrt{3} \text{. } $
9.2.3 Angle between two lines
When we think about more than one line in a plane, then we find that these lines are either intersecting or parallel. Here we will discuss the angle between two lines in terms of their slopes.
Let $L_1$ and $L_2$ be two non-vertical lines with slopes $m_1$ and $m_2$, respectively. If $\alpha_1$ and $\alpha_2$ are the inclinations of lines $L_1$ and $L_2$, respectively. Then
$ m_1=\tan \alpha_1 \text{ and } m_2=\tan \alpha_2 . $
We know that when two lines intersect each other, they make two pairs of vertically opposite angles such that sum of any two adjacent angles is $180^{\circ}$. Let $\theta$ and $\phi$ be the adjacent angles between the lines $L_1$ and $L_2$ (Fig 9.6). Then

$ \theta=\alpha_2-\alpha_1 \text{ and } \alpha_1, \alpha_2 \neq 90^{\circ} \text{. } $
Therefore $\tan \theta=\tan (\alpha_2-\alpha_1)=\frac{\tan \alpha_2-\tan \alpha_1}{1+\tan \alpha_1 \tan \alpha_2}=\frac{m_2-m_1}{1+m_1 m_2} \quad(.$ as $.1+m_1 m_2 \neq 0)$ and $\phi=180^{\circ}-\theta$ so that
$\tan \phi=\tan (180^{\circ}-\theta)=-\tan \theta=-\frac{m_2-m_1}{1+m_1 m_2}$, as $1+m_1 m_2 \neq 0$
Now, there arise two cases:
Case I If $\frac{m_2-m_1}{1+m_1 m_2}$ is positive, then $\tan \theta$ will be positive and $\tan \phi$ will be negative, which means $\theta$ will be acute and $\phi$ will be obtuse.
Case II If $\frac{m_2-m_1}{1+m_1 m_2}$ is negative, then $\tan \theta$ will be negative and $\tan \phi$ will be positive, which means that $\theta$ will be obtuse and $\phi$ will be acute.
Thus, the acute angle (say $\theta$ ) between lines $L_1$ and $L_2$ with slopes $m_1$ and $m_2$, respectively, is given by
$ \tan \theta=|\frac{m_2-m_1}{1+m_1 m_2}|, \text{ as } 1+m_1 m_2 \neq 0 \quad \quad \quad \quad \quad \quad \quad \quad \ldots(1) $
The obtuse angle ( say $\phi$ ) can be found by using $\phi=180^{\circ}-\theta$.
Example 2 If the angle between two lines is $\frac{\pi}{4}$ and slope of one of the lines is $\frac{1}{2}$, find the slope of the other line.
Solution We know that the acute angle $\theta$ between two lines with slopes $m_1$ and $m_2$
is given by $\quad \tan \theta=\left|\frac{m_2-m_1}{1+m_1 m_2} \right| \quad \quad \quad \quad \quad \quad \quad \quad \ldots(1)$
Let $m_1=\frac{1}{2}, m_2=m$ and $\theta=\frac{\pi}{4}$.
Now, putting these values in (1), we get
$ \tan \frac{\pi}{4}=\left|\frac{m-\frac{1}{2}}{1+\frac{1}{2} m}\right| \text{ or } 1=\left|\frac{m-\frac{1}{2}}{1+\frac{1}{2} m}\right| $
which gives $\frac{m-\frac{1}{2}}{1+\frac{1}{2} m}=1$ or $\frac{m-\frac{1}{2}}{1+\frac{1}{2} m}=-1$.
Therefore $m=3$ or $m=-\frac{1}{3}$.
Hence, slope of the other line is 3 or $-\frac{1}{3}$. Fig 9.7 explains the reason of two answers.

Example 3 Line through the points $(-2,6)$ and $(4,8)$ is perpendicular to the line through the points $(8,12)$ and $(x, 24)$. Find the value of $x$.
Solution Slope of the line through the points $(-2,6)$ and $(4,8)$ is
$ m_1=\frac{8-6}{4-(-2)}=\frac{2}{6}=\frac{1}{3} $
Slope of the line through the points $(8,12)$ and $(x, 24)$ is
$ m_2=\frac{24-12}{x-8}=\frac{12}{x-8} $
Since two lines are perpendicular, $m_1 m_2=-1$, which gives
$ \frac{1}{3} \times \frac{12}{x-8}=-1 \text{ or } x=4 \text{. } $
EXERCISE 9.1
1. Draw a quadrilateral in the Cartesian plane, whose vertices are $(-4,5),(0,7)$, $(5,-5)$ and $(-4,-2)$. Also, find its area.
Answer : Let $A B C D$ be the given quadrilateral with vertices $ A($ -4, 5 $), B(0,7), C ( 5, - $5 $)$, and $D$ (4, 2). Then, by plotting $A, B, C$, and $D$ on the Cartesian plane and joining $A B, B C, C D$, and $D A$, the given quadrilateral can be drawn as To find the area of quadrilateral $A B C D$, we draw one diagonal, say $A C$. Accordingly, area $(A B C D)=area(\triangle A B C)+area(\triangle A C D)$ We know that the area of a triangle whose vertices are $(x_1, y_1),(x_2, y_2)$, and $(x_3, y_3)$ is $\frac{1}{2}|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)|$ Therefore, area of $\triangle ABC$
$=\frac{1}{2}|-4(7+5)+0(-5-5)+5(5-7)|$ unit $^{2}$ $=\frac{1}{2}|-4(12)+5(-2)|$ unit $^{2}$ $=\frac{1}{2}|-48-10|$ unit $^{2}$ $=\frac{1}{2}|-58|$ unit $^{2}$ $=\frac{1}{2} \times 58$ unit $^{2}$ $=29$ unit $^{2}$ Area of $\triangle A C D$ $=\frac{1}{2}|-4(-5+2)+5(-2-5)+(-4)(5+5)|$ unit $^{2}$ $=\frac{1}{2}|-4(-3)+5(-7)-4(10)|$ unit $^{2}$ $=\frac{1}{2}|12-35-40|$ unit $^{2}$ $=\frac{1}{2}|-63|$ unit $^{2}$ $=\frac{63}{2}$ unit $^{2}$ Thus, area (ABCD) $
=(29+\frac{63}{2}) \text{ unit }^{2}=\frac{58+63}{2} \text{ unit }^{2}=\frac{121}{2} \text{ unit }^{2}
$Show Answer

Answer : Let $A B C$ be the given equilateral triangle with side $2 a$. Accordingly, $AB=BC=CA=2 a$ Assume that base $BC$ lies along the $y$-axis such that the mid-point of $BC$ is at the origin. i.e., $BO=OC=a$, where $O$ is the origin. Now, it is clear that the coordinates of point $C$ are $(0, a)$, while the coordinates of point $B$ are $(0, - a)$. It is known that the line joining a vertex of an equilateral triangle with the mid-point of its opposite side is perpendicular. Hence, vertex A lies on the $y$-axis. On applying Pythagoras theorem to $\triangle A O C$, we obtain $
\begin{aligned}
& (AC)^{2}=(OA)^{2}+(OC)^{2} \\
& \Rightarrow(2 a)^{2}=(OA)^{2}+a^{2} \\
& \Rightarrow 4 a^{2} - a^{2}=(OA)^{2} \\
& \Rightarrow(OA)^{2}=3 a^{2} \\
& \Rightarrow OA=\sqrt{3} a
\end{aligned}
$ $\therefore$ Coordinates of point $A=( \pm \sqrt{3} a, 0)$ Thus, the vertices of the given equilateral triangle are $(0, a),(0, -{ } a)$, and $(\sqrt{3} a, 0)$ or $(0, a),(0, - a)$, and $(-\sqrt{3} a, 0)$.Show Answer

Answer : The given points are $P(x_1, y_1)$ and $Q(x_2, y_2)$. (i) When PQ is parallel to the $y$-axis, $x_1=x_2$. In this case, distance between $P$ and $Q=\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}}$ $
\begin{aligned}
& =\sqrt{(y_2-y_1)^{2}} \\
& =|y_2-y_1|
\end{aligned}
$ (ii) When PQ is parallel to the $x$-axis, $y_1=y_2$. In this case, distance between $P$ and $Q=\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}}$ $
\begin{aligned}
& =\sqrt{(x_2-x_1)^{2}} \\
& =|x_2-x_1|
\end{aligned}
$Show Answer
Answer : Let $(a, 0)$ be the point on the $x$ axis that is equidistant from the points $(7,6)$ and $(3,4)$. Accordingly, $\sqrt{(7-a)^{2}+(6-0)^{2}}=\sqrt{(3-a)^{2}+(4-0)^{2}}$ $\Rightarrow \sqrt{49+a^{2}-14 a+36}=\sqrt{9+a^{2}-6 a+16}$ $\Rightarrow \sqrt{a^{2}-14 a+85}=\sqrt{a^{2}-6 a+25}$ On squaring both sides, we obtain $a^{2}$ - $14 a+85=a^{2}- 6 a+25$ $\Rightarrow a - 14 a+6 a=25 - 85$ $\Rightarrow $ - $8 a=- 60$ $\Rightarrow a=\frac{60}{8}=\frac{15}{2}$ Thus, the required point on the $x$-axis is $
(\frac{15}{2}, 0)
$Show Answer
Answer : The coordinates of the mid-point of the line segment joining the points $P(0, - 4)$ and $B(8,0)$ are $
(\frac{0+8}{2}, \frac{-4+0}{2})=(4,-2)
$ It is known that the slope $(m)$ of a non-vertical line passing through the points $(x_1, y_1)$ and $(x_2, y_2)$ is given by $m=\frac{y_2-y_1}{x_2-x_1}, x_2 \neq x_1$ Therefore, the slope of the line passing through $(0,0)$ and $ ( 4, \hat{a} 2 ) $ is $\frac{-2-0}{4-0}=\frac{-2}{4}=-\frac{1}{2}$. Hence, the required slope of the line is $-\frac{1}{2}$.Show Answer
Answer : The vertices of the given triangle are A $(4,4), B(3,5)$, and C (-1, -1). It is known that the slope $(m)$ of a non-vertical line passing through the points $(x_1, y_1)$ and $(x_2, y_2)$ is given by $m=\frac{y_2-y_1}{x_2-x_1}, x_2 \neq x_1$ $\therefore$ Slope of $AB(m_1)=\frac{5-4}{3-4}=-1$ Slope of $BC(m_2)=\frac{-1-5}{-1-3}=\frac{-6}{-4}=\frac{3}{2}$ Slope of CA $(m_3)=\frac{4+1}{4+1}=\frac{5}{5}=1$ It is observed that $m_1 m_3=\hat{a} $ 1 This shows that line segments $A B$ and $C A$ are perpendicular to each other i.e., the given triangle is right-angled at $A(4,4)$. Thus, the points $(4,4),(3,5)$, and (1, 1 ) are the vertices of a right-angled triangle.Show Answer
Answer : If a line makes an angle of $30^{\circ}$ with the positive direction of the $y$-axis measured anticlockwise, then the angle made by the line with the positive direction of the $x$-axis measured anticlockwise is $90^{\circ}+30^{\circ}=120^{\circ}$. Thus, the slope of the given line is $\tan 120^{\circ}=\tan (180^{\circ} - 60^{\circ})=- \tan 60^{\circ}=-\sqrt{3}$Show Answer

Answer : Let points ( $$ - $2, $ -1), $(4,0),(3,3)$, and ( $-$3,2 ) be respectively denoted by A, B, C, and $D$. Slope of $A B=\frac{0+1}{4+2}=\frac{1}{6}$ Slope of $CD=\frac{2-3}{-3-3}=\frac{-1}{-6}=\frac{1}{6}$ $\Rightarrow$ Slope of $A B=$ Slope of $C D$ $\Rightarrow A B$ and $C D$ are parallel to each other. Now, slope of $BC=\frac{3-0}{3-4}=\frac{3}{-1}=-3$ Slope of $AD=\frac{2+1}{-3+2}=\frac{3}{-1}=-3$ $\Rightarrow$ Slope of $BC=$ Slope of $AD$ $\Rightarrow B C$ and $A D$ are parallel to each other. Therefore, both pairs of opposite sides of quadrilateral $A B C D$ are parallel. Hence, $A B C D$ is a parallelogram. Thus, points (-2, -1), $(4,0),(3,3)$, and (-3,2) are the vertices of a parallelogram.Show Answer

Answer : The slope of the line joining the points ($ 3, \hat{a} $ 1 ) and ( $4, \hat{a} $ 2 ) is $
m=\frac{-2-(-1)}{4-3}=-2+1=-1
$ Now, the inclination $(\theta)$ of the line joining the points $(3, -$1 $)$ and $(4, -{ } 2)$ is given by
$\tan \theta=- 1$ $\Rightarrow \theta=(90^{\circ}+45^{\circ})=135^{\circ}$ Thus, the angle between the $x$-axis and the line joining the points $(3, $ - 1 $)$ and ( $ 4, - $ 2 ) is $ 135^{\circ} $.Show Answer
Answer : Let $m_1$ and $m$ be the slopes of the two given lines such that $m_1=2 m$. We know that if $\theta$ isthe angle between the lines $l_1$ and $I_2$ with slopes $m_1$ and $m_2$, then $
\tan \theta=|\frac{m_2-m_1}{1+m_1 m_2}|
$ It is given that the tangent of the angle between the two lines is $\frac{1}{3}$. $\therefore \frac{1}{3}=|\frac{m-2 m}{1+(2 m) \cdot m}|$ $\Rightarrow \frac{1}{3}=|\frac{-m}{1+2 m^{2}}|$ $\Rightarrow \frac{1}{3}=\frac{-m}{1+2 m^{2}}$ or $\frac{1}{3}=-(\frac{-m}{1+2 m^{2}})=\frac{m}{1+2 m^{2}}$ If $m=$ - 1 , then the slopes of the lines are - 1 and - 2 . If $m=-\frac{1}{2}$, then the slopes of the lines are $-\frac{1}{2}$ and -1. Case II $\frac{1}{3}=\frac{m}{1+2 m^{2}}$ $\Rightarrow 2 m^{2}+1=3 m$ $\Rightarrow 2 m^{2}-3 m+1=0$ $\Rightarrow 2 m^{2}-2 m-m+1=0$ $\Rightarrow 2 m(m-1)-1(m-1)=0$ $\Rightarrow(m-1)(2 m-1)=0$ $\Rightarrow m=1$ or $m=\frac{1}{2}$ If $m=1$, then the slopes of the lines are 1 and 2 . If $m=\frac{1}{2}$, then the slopes of the lines are $\frac{1}{2}$ and 1 Hence, the slopes of the lines are - 1 and - 2 or $\quad-\frac{1}{2}$ and - 1 or 1 and 2 or $\frac{1}{2}$ and 1 .Show Answer
$ k-y_1=m(h-x_1) . $
Show Answer
Answer :
The slope of the line passing through $(x_1, y_1)$ and $(h, k)$ is $\frac{k-y_1}{h-x_1}$.
It is given that the slope of the line is $m$.
$\therefore \frac{k-y_1}{h-x_1}=m$
$\Rightarrow k-y_1=m(h-x_1)$
Hence, $k-y_1=m(h-x_1)$
9.3 Various Forms of the Equation of a Line
We know that every line in a plane contains infinitely many points on it. This relationship between line and points leads us to find the solution of the following problem:
How can we say that a given point lies on the given line? Its answer may be that for a given line we should have a definite condition on the points lying on the line. Suppose $P(x, y)$ is an arbitrary point in the XY-plane and $L$ is the given line. For the equation of $L$, we wish to construct a statement or condition for the point $P$ that is true, when $P$ is on $L$, otherwise false. Of course the statement is merely an algebraic equation involving the variables $x$ and $y$. Now, we will discuss the equation of a line under different conditions.
9.3.1 Horizontal and vertical lines
If a horizontal line $L$ is at a distance $a$ from the $x$ axis then ordinate of every point lying on the line is either $a$ or $-a$ [Fig 9.8 (a)]. Therefore, equation of the line $L$ is either $y=a$ or $y=-a$. Choice of sign will depend upon the position of the line according as the line is above or below the $y$-axis. Similarly, the equation of a vertical line at a distance $b$ from the $y$-axis is either $x=b$ or $x=-b$ [ Fig 9.8(b)].

Example 4 Find the equations of the lines parallel to axes and passing through $(-2,3)$.

Solution Position of the lines is shown in the Fig 9.9. The $y$-coordinate of every point on the line parallel to $x$-axis is 3 , therefore, equation of the line parallel tox-axis and passing through $(-2,3)$ is $y=3$. Similarly, equation of the line parallel to $y$-axis and passing through $(-2,3)$ is $x=-2$.
9.3.2 Point-slope form
Suppose that $P_0(x_0, y_0)$ is a fixed point on a non-vertical line $L$, whose slope is $m$. Let $P(x, y)$ be an arbitrary point on L (Fig 9.10).

Then, by the definition, the slope of $L$ is given by
$ m=\frac{y-y_0}{x-x_0} \text{, i.e., } y-y_0=m(x-x_0) \quad \quad \quad \quad \quad \quad \ldots (1) $
Since the point $P_0(x_0, y_0)$ along with all points $(x, y)$ on $L$ satisfies (1) and no other point in the plane satisfies (1). Equation (1) is indeed the equation for the given line $L$.
Thus, the point $(x, y)$ lies on the line with slope $m$ through the fixed point $(x_0, y_0)$, if and only if, its coordinates satisfy the equation
$ y-y_0=m(x-x_0) $
Example 5 Find the equation of the line through $(-2,3)$ with slope -4 .
Solution Here $m=-4$ and given point $(x_0, y_0)$ is $(-2,3)$.
By slope-intercept form formula (1) above, equation of the given line is
$y-3=-4(x+2)$ or
$4 x+y+5=0$, which is the required equation.
9.3.3 Two-point form
Let the line $L$ passes through two given points $P_1(x_1, y_1)$ and $P_2(x_2, y_2)$. Let $P(x, y)$ be a general point on $L$ (Fig 9.11).

The three points $P_1, P_2$ and $P$ are collinear, therefore, we have
Fig 9.11 slope of $P_1 P=$ slope of $P_1 P_2$
$ \text{ i.e., } \quad \frac{y-y_1}{x-x_1}=\frac{y_2-y_1}{x_2-x_1}, \quad \text{ or } \quad y-y_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1) \text{. } $
Thus, equation of the line passing through the points $(x_1, y_1)$ and $(x_2, y_2)$ is given by
$ y-y_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1) \quad \quad \quad \quad \quad \quad \quad \quad \ldots (2) $
Example 6 Write the equation of the line through the points $(1,-1)$ and $(3,5)$.
Solution Here $x_1=1, y_1=-1, x_2=3$ and $y_2=5$. Using two-point form (2) above for the equation of the line, we have
$ y-(-1)=\frac{5-(-1)}{3-1}(x-1) $
or
$ -3 x+y+4=0 \text{, which is the required equation. } $
9.3.4 Slope-intercept form
Sometimes a line is known to us with its slope and an intercept on one of the axes. We will now find equations of such lines.
Case I Suppose a line $L$ with slope $m$ cuts the $y$-axis at a distance $c$ from the origin (Fig 9.12). The distance $c$ is called the $y$ intercept of the line L. Obviously, coordinates of the point where the line meet the $y$-axis are $(0, c)$. Thus, $L$ has slope $m$ and passes through a fixed point $(0, c)$. Therefore, by point-slope form, the equation of $L$ is

$ y-c=m(x-0) \text{ or } y=m x+c $
Thus, the point $(x, y)$ on the line with slope $m$ and $y$-intercept $c$ lies on the line if and only if
$ y=m x+c \quad \quad \quad \quad \quad \quad \ldots(3) $
Note that the value of $c$ will be positive or negative according as the intercept is made on the positive or negative side of the $y$-axis, respectively.
Case II Suppose line $L$ with slope $m$ makes $x$-intercept $d$. Then equation of $L$ is
$ y=m(x-d) \quad \quad \quad \quad \quad \quad \ldots(4) $
Students may derive this equation themselves by the same method as in Case I.
Example 7 Write the equation of the lines for which $\tan \theta=\frac{1}{2}$, where $\theta$ is the inclination of the line and (i) $y$-intercept is $-\frac{3}{2}$ (ii) $x$-intercept is 4 .
Solution (i) Here, slope of the line is $m=\tan \theta=\frac{1}{2}$ and $y$ - intercept $c=-\frac{3}{2}$.
Therefore, by slope-intercept form (3) above, the equation of the line is
$ y=\frac{1}{2} x-\frac{3}{2} \text{ or } 2 y-x+3=0 \text{, } $
which is the required equation.
(ii) Here, we have $m=\tan \theta=\frac{1}{2}$ and $d=4$.
Therefore, by slope-intercept form (4) above, the equation of the line is
$ y=\frac{1}{2}(x-4) \text{ or } 2 y-x+4=0 \text{, } $
which is the required equation.
9.3.5 Intercept - form
Suppose a line L makes $x$-intercept $a$ and $y$-intercept $b$ on the axes. Obviously $L$ meets $x$-axis at the point $(a, 0)$ and $y$-axis at the point $(0, b)$ (Fig .9.13). By two-point form of the equation of the line, we have

$ \begin{aligned} & y-0=\frac{b-0}{0-a}(x-a) \text{ or } a y=-b x+a b, \\ & \text{ i.e., } \quad \frac{x}{a}+\frac{y}{b}=1 . \end{aligned} $
Thus, equation of the line making intercepts $a$ and $b$ on $x$-and $y$-axis, respectively, is
$ \frac{x}{a}+\frac{y}{b}=1 \quad \quad \quad \quad \quad \quad \quad \ldots (5) $
Example 8 Find the equation of the line, which makes intercepts -3 and 2 on the $x$ - and $y$-axes respectively.
Solution Here $a=-3$ and $b=2$. By intercept form (5) above, equation of the line is
$ \frac{x}{-3}+\frac{y}{2}=1 \quad \text{ or } \quad 2 x-3 y+6=0 $
Any equation of the form $A x+B y+C=0$, where $A$ and $B$ are not zero simultaneously is called general linear equation or general equation of a line.
EXERCISE 9.2
In Exercises 1 to 8, find the equation of the line which satisfy the given conditions:
1. Write the equations for the $x$-and $y$-axes.
Answer : The $y$-coordinate of every point on the $x$-axis is 0 . Therefore, the equation of the $x$-axis is $y=0$. The $x$-coordinate of every point on the $y$-axis is 0 . Therefore, the equation of the $y$-axis is $x=0$.Show Answer
Answer : We know that the equation of the line passing through point $(x_0, y_0)$, whose slope is $m$, is $(y-y_0)=m(x-x_0)$. Thus, the equation of the line passing through point ( $-$ “ 4,3$)$, whose slope is $\frac{1}{2}$, is $
\begin{aligned}
& (y-3)=\frac{1}{2}(x+4) \\
& 2(y-3)=x+4 \\
& 2 y-6=x+4 \\
& \text{ i.e., } x-2 y+10=0
\end{aligned}
$Show Answer
Answer : We know that the equation of the line passing through point $(x_0, y_0)$, whose slope is $m$, is $(y-y_0)=m(x-x_0)$. Thus, the equation of the line passing through point $(0,0)$, whose slope is $m$, is ( $y$ - 0$)=m(x$ - 0$)$ i.e., $y=m x$Show Answer
Answer : The slope of the line that inclines with the $x$-axis at an angle of $75^{\circ}$ is $m=\tan 75^{\circ}$ $\Rightarrow m=\tan (45^{\circ}+30^{\circ})=\frac{\tan 45^{\circ}+\tan 30^{\circ}}{1-\tan 45^{\circ} \cdot \tan 30^{\circ}}=\frac{1+\frac{1}{\sqrt{3}}}{1-1 \cdot \frac{1}{\sqrt{3}}}=\frac{\frac{\sqrt{3}+1}{\sqrt{3}}}{\frac{\sqrt{3}-1}{\sqrt{3}}}=\frac{\sqrt{3}+1}{\sqrt{3}-1}$ We know that the equation of the line passing through point $(x_0, y_0)$, whose slope is $m$, is $(y-y_0)=m(x-x_0)$. Thus, if a line passes though $(2,2 \sqrt{3})$ and inclines with the $x$-axis at an angle of $75^{\circ}$, then the equation of the line is given as $
\begin{aligned}
& (y-2 \sqrt{3})=\frac{\sqrt{3}+1}{\sqrt{3}-1}(x-2) \\
& (y-2 \sqrt{3})(\sqrt{3}-1)=(\sqrt{3}+1)(x-2) \\
& y(\sqrt{3}-1)-2 \sqrt{3}(\sqrt{3}-1)=x(\sqrt{3}+1)-2(\sqrt{3}+1) \\
& (\sqrt{3}+1) x-(\sqrt{3}-1) y=2 \sqrt{3}+2-6+2 \sqrt{3} \\
& (\sqrt{3}+1) x-(\sqrt{3}-1) y=4 \sqrt{3}-4 \\
& \text{ i.e., }(\sqrt{3}+1) x-(\sqrt{3}-1) y=4(\sqrt{3}-1)
\end{aligned}
$Show Answer
Answer : It is known that if a line with slope $m$ makes $x$-intercept $d$, then the equation of the line is given as $y=m(x-d)$ For the line intersecting the $x$-axis at a distance of 3 units to the left of the origin, $d=-3$. The slope of the line is given as $m=-2$ Thus, the required equation of the given line is $y=-2[x-(-3)]$ $y=-2 x-6$ i.e., $2 x+y+6=0$Show Answer
Answer : It is known that if a line with slope $m$ makes $y$-intercept $c$, then the equation of the line is given as $y=m x+c$ Here, $c=2$ and $m=\tan 30^{\circ}$ $
=\frac{1}{\sqrt{3}} \text{. }
$ Thus, the required equation of the given line is $
\begin{aligned}
& y=\frac{1}{\sqrt{3}} x+2 \\
& y=\frac{x+2 \sqrt{3}}{\sqrt{3}} \\
& \sqrt{3} y=x+2 \sqrt{3} \\
& \text{ i.e., } x-\sqrt{3} y+2 \sqrt{3}=0
\end{aligned}
$Show Answer
Answer : It is known that the equation of the line passing through points $(x_1, y_1)$ and $(x_2, y_2)$ is $y-y_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1)$. Therefore, the equation of the line passing through the points ( $.-{ }^{\text{" }} 1,1,1) $ and (2, - 4 ) is $(y-1)=\frac{-4-1}{2+1}(x+1)$ $(y-1)=\frac{-5}{3}(x+1)$ $3(y-1)=-5(x+1)$ $3 y-3=-5 x-5$ i.e., $5 x+3 y+2=0$Show Answer
Answer : It is given that the vertices of $\triangle P Q R$ are $P(2,1), Q(\hat{a}.$ “" $.^{2}, 3)$, and $R(4,5)$. Let $RL$ be the median through vertex $R$. Accordingly, $L$ is the mid-point of $PQ$. By mid-point formula, the coordinates of point $L$ are given by $(\frac{2-2}{2}, \frac{1+3}{2})=(0,2)$ It is known that the equation of the line passing through points $(x_1, y_1)$ and $(x_2, y_2)$ is $y-y_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1)$. Therefore, the equation of $RL$ can be determined by substituting $(x_1, y_1)=(4,5)$ and $(x_2, y_2)=(0,2)$. Hence, $y-5=\frac{2-5}{0-4}(x-4)$ $\Rightarrow y-5=\frac{-3}{-4}(x-4)$ $\Rightarrow 4(y-5)=3(x-4)$ $\Rightarrow 4 y-20=3 x-12$ $\Rightarrow 3 x-4 y+8=0$ Thus, the required equation of the median through vertex $R$ is $3 x-4 y+8=0$.Show Answer

Answer : The slope of the line joining the points $(2,5)$ and $( - 3,6)$ is $
m=\frac{6-5}{-3-2}=\frac{1}{-5}
$ We know that two non-vertical lines are perpendicular to each other if and only if their slopes are negative reciprocals of each other. Therefore, slope of the line perpendicular to the line through the points $(2,5)$ and (-3,6 ) $
=-\frac{1}{m}=-\frac{1}{(\frac{-1}{5})}=5
$ Now, the equation of the line passing through point ( $- 3,5$ ), whose slope is 5 , is $
\begin{aligned}
& (y-5)=5(x+3) \\
& y-5=5 x+15 \\
& \text{ i.e., } 5 x-y+20=0
\end{aligned}
$Show Answer
Answer : According to the section formula, the coordinates of the point that divides the line segment joining the points $(1,0)$ and $(2,3)$ in the ratio $1: n$ is given by $
(\frac{n(1)+1(2)}{1+n}, \frac{n(0)+1(3)}{1+n})=(\frac{n+2}{n+1}, \frac{3}{n+1})
$ The slope of the line joining the points $(1,0)$ and $(2,3)$ is $
m=\frac{3-0}{2-1}=3
$ We know that two non-vertical lines are perpendicular to each other if and only if their slopes are negative reciprocals of each other. Therefore, slope of the line that is perpendicular to the line joining the points $(1,0)$ and $(2,3) \quad m \quad 3$ $
=-\frac{1}{m}=-\frac{1}{3}
$ Now, the equation of the line passing through $(\frac{n+2}{n+1}, \frac{3}{n+1})$ and whose slope is $-\frac{1}{3}$ is given by $
\begin{aligned}
& (y-\frac{3}{n+1})=\frac{-1}{3}(x-\frac{n+2}{n+1}) \\
& \Rightarrow 3[(n+1) y-3]=-[x(n+1)-(n+2)] \\
& \Rightarrow 3(n+1) y-9=-(n+1) x+n+2 \\
& \Rightarrow(1+n) x+3(1+n) y=n+11
\end{aligned}
$Show Answer
Answer : The equation of a line in the intercept form is $$
\begin{equation*}
\frac{x}{a} + \frac{y}{b}=1 \tag{i}
\end{equation*}
$$ Here, $a$ and $b$ are the intercepts on $x$ and $y$ axes respectively. It is given that the line cuts off equal intercepts on both the axes. This means that $a=b$. Accordingly, equation (i) reduces to $$
\begin{align*}
& \frac{x}{a} + \frac{y}{a}=1 \\
& \Rightarrow x+y=a
\end{align*}
$$ Since the given line passes through point $(2,3)$, equation (ii) reduces to $2+3=a \Rightarrow a=5$ On substituting the value of $a$ in equation (ii), we obtain $x+y=5$, which is the required equation of the lineShow Answer
Answer : The equation of a line in the intercept form is $$
\begin{equation*}
\frac{x}{a} + \frac{y}{b}=1 \tag{i}
\end{equation*}
$$ Here, $a$ and $b$ are the intercepts on $x$ and $y$ axes respectively. It is given thata $+b=9 \Rightarrow b=9$ - $a \ldots$ (ii) From equations (i) and (ii), we obtain $$
\begin{equation*}
\frac{x}{a} + \frac{y}{9-a}=1 \tag{iii}
\end{equation*}
$$ It is given that the line passes through point $(2,2)$. Therefore, equation (iii) reduces to $$
\begin{aligned}
& \frac{2}{a} + \frac{2}{9-a}=1 \\
& \Rightarrow 2(\frac{1}{a} + \frac{1}{9-a})=1 \\
& \Rightarrow 2(\frac{9-a+a}{a(9-a)})=1 \\
& \Rightarrow \frac{18}{9 a-a^{2}}=1 \\
& \Rightarrow 18=9 a-a^{2} \\
& \Rightarrow a^{2}-9 a+18=0 \\
& \Rightarrow a^{2}-6 a-3 a+18=0 \\
& \Rightarrow a(a-6)-3(a-6)=0 \\
& \Rightarrow(a-6)(a-3)=0 \\
& \Rightarrow a=6 \text{ or } a=3
\end{aligned}
$$ If $a=6$ and $b=9$ - $6=3$, then the equation of the line is $\frac{x}{6}+\frac{y}{3}=1 \Rightarrow x+2 y-6=0$ If $a=3$ and $b=9 - 3=6$, then the equation of the line is $\frac{x}{3}+\frac{y}{6}=1 \Rightarrow 2 x+y-6=0$Show Answer
Answer : The slope of the line making an angle $\frac{2 \pi}{3}$ with the positive $x$-axis is $\quad m=\tan (\frac{2 \pi}{3})=-\sqrt{3}$ Now, the equation of the line passing through point $(0,2)$ and having a slope $-\sqrt{3}$ is $(y-2)=-\sqrt{3}(x-0)$. $y-2=-\sqrt{3} x$ i.e., $\sqrt{3} x+y-2=0$ The slope of line parallel to line $\sqrt{3} x+y-2=0$ is $-\sqrt{3}$. It is given that the line parallel to line $\sqrt{3} x+y-2=0$ crosses the $y$-axis 2 units below the origin i.e., it passes through point ( 0, - 2 ). Hence, the equation of the line passing through point ( $0, -$ “ 2 ) and having a slope $-\sqrt{3}$ is $y-(-2)=-\sqrt{3}(x-0)$ $y+2=-\sqrt{3} x$ $\sqrt{3} x+y+2=0$Show Answer
Answer : The slope of the line joining the origin $(0,0)$ and point (-2,9) is $m_1=\frac{9-0}{-2-0}=-\frac{9}{2}$ Accordingly, the slope of the line perpendicular to the line joining the origin and point (- 2,9 ) is $m_2=-\frac{1}{m_1}=-\frac{1}{(-\frac{9}{2})}=\frac{2}{9}$ Now, the equation of the line passing through point $($ - 2,9$)$ and having a slope $m_2$ is $
\begin{aligned}
& (y-9)=\frac{2}{9}(x+2) \\
& 9 y-81=2 x+4 \\
& \text{ i.e., } 2 x-9 y+85=0
\end{aligned}
$Show Answer
Answer : It is given that when $C=20$, the value of $L$ is 124.942 , whereas when $C=110$, the value of $L$ is 125.134 . Accordingly, points $(20,124.942)$ and $(110,125.134)$ satisfy the linear relation between $L$ and $C$. Now, assuming $C$ along the $x$-axis and $L$ along the $y$-axis, we have two points i.e., $(20,124.942)$ and $(110,125.134)$ in the $X Y$ plane. Therefore, the linear relation between $L$ and $C$ is the equation of the line passing through points $(20,124.942)$ and $(110,125.134)$. $(L - 124.942)=\frac{125.134-124.942}{110-20}(C-20)$ $L-124.942=\frac{0.192}{90}(C-20)$ i.e., $L=\frac{0.192}{90}(C-20)+124.942$, which is the required linear relationShow Answer
Answer : The relationship between selling price and demand is linear. Assuming selling price per litre along the $x$-axis and demand along the $y$-axis, we have two points i.e., $(14,980)$ and $(16,1220)$ in the XY plane that satisfy the linear relationship between selling price and demand. Therefore, the linear relationship between selling price per litre and demand is the equation of the line passing through points $(14,980)$ and $(16,1220)$. $
\begin{aligned}
& y-980=\frac{1220-980}{16-14}(x-14) \\
& y-980=\frac{240}{2}(x-14) \\
& y-980=120(x-14) \\
& \text{ i.e., } y=120(x-14)+980
\end{aligned}
$ When $x=$ Rs $17 /$ litre, $
\begin{aligned}
& y=120(17-14)+980 \\
& \Rightarrow y=120 \times 3+980=360+980=1340
\end{aligned}
$ Thus, the owner of the milk store could sell 1340 litres of milk weekly at Rs 17/litre.Show Answer
Answer : Let $A B$ be the line segment between the axes and let $P(a, b)$ be its mid-point. Let the coordinates of $A$ and $B$ be $(0, y)$ and $(x, 0)$ respectively. Since $P(a, b)$ is the mid-point of $AB$, $(\frac{0+x}{2}, \frac{y+0}{2})=(a, b)$ $\Rightarrow(\frac{x}{2}, \frac{y}{2})=(a, b)$ $\Rightarrow \frac{x}{2}=a$ and $\frac{y}{2}=b$ $\therefore x=2 a$ and $y=2 b$ Thus, the respective coordinates of A and B are $(0,2 b)$ and $(2 a, 0)$. The equation of the line passing through points $(0,2 b)$ and $(2 a, 0)$ is $(y-2 b)=\frac{(0-2 b)}{(2 a-0)}(x-0)$ $y-2 b=\frac{-2 b}{2 a}(x)$ $a(y-2 b)=-b x$ $a y-2 a b=-b x$ i.e., $b x+a y=2 a b$ On dividing both sides by $a b$, we obtain
$\frac{b x}{a b}+\frac{a y}{a b}=\frac{2 a b}{a b}$ $\Rightarrow \frac{x}{a}+\frac{y}{b}=2$ Thus, the equation of the line is $\frac{x}{a}+\frac{y}{b}=2$.Show Answer

Answer : Let $A B$ be the line segment between the axes such that point $R(h, k)$ divides $A B$ in the ratio 1: 2 . Let the respective coordinates of $A$ and $B$ be $(x, 0)$ and $(0, y)$. Since point $R(h, k)$ divides $AB$ in the ratio $1: 2$, according to the section formula, $(h, k)=(\frac{1 \times 0+2 \times x}{1+2}, \frac{1 \times y+2 \times 0}{1+2})$ $\Rightarrow(h, k)=(\frac{2 x}{3}, \frac{y}{3})$ $\Rightarrow h=\frac{2 x}{3}$ and $k=\frac{y}{3}$ $\Rightarrow x=\frac{3 h}{2}$ and $y=3 k$ Therefore, the respective coordinates of $A$ and $B$ are $(\frac{3 h}{2}, 0)$ and $(0,3 k)$. Now, the equation of line $AB$ passing through points $(\frac{3 h}{2}, 0)$ and $(0,3 k)$ is
$(y-0)=\frac{3 k-0}{0-\frac{3 h}{2}}(x-\frac{3 h}{2})$ $y=-\frac{2 k}{h}(x-\frac{3 h}{2})$ $h y=-2 k x+3 h k$ i.e., $2 k x+h y=3 h k$ Thus, the required equation of the line is $2 k x+h y=3 h k$.Show Answer

Show Answer
Answer :
In order to show that points $(3,0)$, $ (-2,- 2 )$ , and $(8,2)$ are collinear, it suffices to show that the line passing through points $(3,0)$ and $ (-2 , - 2 )$ also passes through point $(8,2)$.
The equation of the line passing through points $(3,0)$ and $( -2, - 2 )$ is
$ \begin{aligned} & (y-0)=\frac{(-2-0)}{(-2-3)}(x-3) \\ & y=\frac{-2}{-5}(x-3) \\ & 5 y=2 x-6 \\ & \text{ i.e., } 2 x-5 y=6 \end{aligned} $
It is observed that at $x=8$ and $y=2$,
L.H.S. $=2 \times 8 $ $ - 5 \times 2=16$ - $10=6=$ R.H.S.
Therefore, the line passing through points $(3,0)$ and ( $.- 2, - 2)$ also passes through point $(8,2)$. Hence, points $(3$, $0)$, (-2, -2), and (8, 2) are collinear.
9.4 Distance of a Point From a Line
The distance of a point from a line is the length of the perpendicular drawn from the point to the line. Let $L: A x+By+C=0$ be a line, whose distance from the point $P(x_1, y_1)$ is $d$. Draw a perpendicular PM from the point $P$ to the line $L$ (Fig 9.14). If the

line meets the $x$-and $y$-axes at the points $Q$ and $R$, respectively. Then, coordinates of the points are $Q(-\frac{C}{A}, 0)$ and $R(0,-\frac{C}{B})$. Thus, the area of the triangle $P Q R$ is given by
$ \text{ area }(\Delta PQR)=\frac{1}{2} PM \cdot QR \text{, which gives } PM=\frac{2 area(\Delta PQR)}{QR} \quad \quad \quad \ldots (1) $
Also, area $(\Delta PQR)=\frac{1}{2}\left|x_1(0+\frac{C}{B})+(-\frac{C}{A})(-\frac{C}{B}-y_1)+0(y_1-0)\right|$
$ =\frac{1}{2}|x_1 \frac{C}{B}+y_1 \frac{C}{A}+\frac{C^{2}}{AB}| $
or 2 area $(\Delta PQR)=|\frac{C}{AB}| \cdot|A _{x_1}+B y_1+C|$, and
$ QR=\sqrt{(0+\frac{C}{A})^{2}+(\frac{C}{B}-0)^{2}}=|\frac{C}{AB}| \sqrt{A^{2}+B^{2}} $
Substituting the values of area $(\triangle PQR)$ and $QR$ in (1), we get
$ PM=\frac{|A x_1+B y_1+C|}{\sqrt{A^{2}+B^{2}}} $
or
$ d=\frac{|A x_1+B y_1+C|}{\sqrt{A^{2}+B^{2}}} . $
Thus, the perpendicular distance $(d)$ of a line $A x+B y+C=0$ from a point $(x_1, y_1)$ is given by
$ d=\frac{|A x_1+B y_1+C|}{\sqrt{A^{2}+B^{2}}} . $
9.4.1 Distance between two parallel lines
We know that slopes of two parallel lines are equal.Therefore, two parallel lines can be taken in the form
$\quad \quad \quad\quad y=m x+c_1 \quad \quad \quad \quad \quad \ldots (1)$
and $\quad \quad \quad y=m x+c_2 \quad \quad \quad \quad \quad \ldots (2)$
Line (1) will intersect $x$-axis at the point $A(-\frac{c_1}{m}, 0)$ as shown in Fig 9.15.

Distance between two lines is equal to the length of the perpendicular from point A to line (2). Therefore, distance between the lines (1) and (2) is
$ \frac{|(-m)(-\frac{c_1}{m})+(-c_2)|}{\sqrt{1+m^{2}}} \text{ or } d=\frac{|c_1-c_2|}{\sqrt{1+m^{2}}} \text{. } $
Thus, the distance $d$ between two parallel lines $y=m x+c_1$ and $y=m x+c_2$ is given by
$ d=\frac{|c_1-c_2|}{\sqrt{1+m^{2}}} $
If lines are given in general form, i.e., $A x+B y+C_1=0$ and $A x+B y+C_2=0$,
then above formula will take the form $d=\frac{|C_1-C_2|}{\sqrt{A^{2}+B^{2}}}$
Students can derive it themselves.
Example 9 Find the distance of the point $(3,-5)$ from the line $3 x-4 y-26=0$.
Solution Given line is $3 x-4 y-26=0$
Comparing (1) with general equation of line $A x+B y+C=0$, we get
$ A=3, B=-4 \text{ and } C=-26 $
Given point is $(x_1, y_1)=(3,-5)$. The distance of the given point from given line is
$ d=\frac{|A x_1+B y_1+C|}{\sqrt{A^{2}+B^{2}}}=\frac{|3.3+(-4)(-5)-26|}{\sqrt{3^{2}+(-4)^{2}}}=\frac{3}{5} . $
Example 10 Find the distance between the parallel lines $3 x-4 y+7=0$ and
$ 3 x-4 y+5=0 $
Solution Here $A=3, B=-4, C_1=7$ and $C_2=5$. Therefore, the required distance is
$ \begin{aligned} & d=\frac{|7-5|}{\sqrt{3^{2}+(-4)^{2}}}=\frac{2}{5} . \\ & \text{ EXERCISE } 9.3 \end{aligned} $
EXERCISE 9.3
1. Reduce the following equations into slope - intercept form and find their slopes and the $y$ - intercepts.
(i) $x+7 y=0$,
(ii) $6 x+3 y-5=0$,
(iii) $y=0$.
Answer : (i) The given equation is $x+7 y=0$. It can be written as $y=-\frac{1}{7} x+0$ This equation is of the form $y=m x+c$, where $
m=-\frac{1}{7} \text{ and } c=0
$ Therefore, equation (1) is in the slope-intercept form, where the slope and the $y$-intercept are $-\frac{1}{7}$ and 0 respectively. (ii) The given equation is $6 x+3 y -5=0$. It can be written as $y=\frac{1}{3}(-6 x+5)$ $y=-2 x+\frac{5}{3}$ This equation is of the form $y=m x+c$, where $m=-2$ and $c=\frac{5}{3}$. Therefore, equation (2) is in the slope-intercept form, where the slope and the $y$-intercept are- 2 and $\frac{5}{3}$ respectively. (iii) The given equation is $y=0$. It can be written as $y=0 . x+0$ This equation is of the form $y=m x+c$, where $m=0$ and $c=0$. Therefore, equation (3) is in the slope-intercept form, where the slope and the $y$-intercept are 0 and 0 respectively.Show Answer
(i) $3 x+2 y-12=0$,
(ii) $4 x-3 y=6$,
(iii) $3 y+2=0$.
Answer : (i) The given equation is $3 x+2 y$ - $12=0$. It can be written as $3 x+2 y=12$ $\frac{3 x}{12}+\frac{2 y}{12}=1$
i.e., $\frac{x}{4}+\frac{y}{6}=1$ This equation is of the form $\frac{x}{a}+\frac{y}{b}=1$, where $a=4$ and $b=6$. Therefore, equation (1) is in the intercept form, where the intercepts on the $x$ and $y$ axes are 4 and 6 respectively. (ii) The given equation is $4 x - 3 y=6$. It can be written as $\frac{4 x}{6}-\frac{3 y}{6}=1$ $\frac{2 x}{3}-\frac{y}{2}=1$ i.e., $\frac{x}{(\frac{3}{2})}+\frac{y}{(-2)}=1$ This equation is of the form $\frac{x}{a}+\frac{y}{b}=1$, where $a=\frac{3}{2}$ and $b=-$2 . Therefore, equation (2) is in the intercept form, where the intercepts on the $x$ and $y$ axes are $\frac{3}{2}$ and -2 respectively. (iii) The given equation is $3 y+2=0$. It can be written as $3 y=-2$ i.e., $\frac{y}{(-\frac{2}{3})}=1$ This equation is of the form $\frac{x}{a}+\frac{y}{b}=1$, where $a=0$ and $b=-\frac{2}{3}$. Therefore, equation (3) is in the intercept form, where the intercept on the $y$-axis is $-\frac{2}{3}$ and it has no intercept on the $x$-axis.Show Answer
Answer : The given equation of the line is $12(x+6)=5(y - 2)$. $\Rightarrow 12 x+72=5 y$ 10 $\Rightarrow 12 x - 5 y+82=0$.. On comparing equation (1) with general equation of line $A x+B y+C=0$, we obtain $A=12, B=$ - 5 , and $C=82$. It is known that the perpendicular distance ( $d$ ) of a line $A x+B y+C=0$ from a point $(x_1, y_1)$ is given by $d=\frac{|A x_1+B y_1+C|}{\sqrt{A^{2}+B^{2}}}$. The given point is $(x_1, y_1)=(- 1,1)$. Therefore, the distance of point $( - 1,1 )$ from the given line $=\frac{|12(-1)+(-5)(1)+82|}{\sqrt{(12)^{2}+(-5)^{2}}}$ units $=\frac{|-12-5+82|}{\sqrt{169}}$ units $=\frac{|65|}{13}$ units $=5$ unitsShow Answer
Answer : The given equation of line is $\frac{x}{3}+\frac{y}{4}=1$ or, $4 x+3 y-12=0$ On comparing equation (1) with general equation of line $A x+B y+C=0$, we obtain $A=4, B=3$, and $C=$ - 12 . Let $(a, 0)$ be the point on the $x$-axis whose distance from the given line is 4 units. It is known that the perpendicular distance $(d)$ of a line $A x+B y+C=0$ from a point $(x_1, y_1)$ is given by $d=\frac{|A x_1+B y_1+C|}{\sqrt{A^{2}+B^{2}}}$. Therefore, $4=\frac{|4 a+3 \times 0-12|}{\sqrt{4^{2}+3^{2}}}$ $\Rightarrow 4=\frac{|4 a-12|}{5}$ $\Rightarrow|4 a-12|=20$ $\Rightarrow \pm(4 a-12)=20$ $\Rightarrow(4 a-12)=20$ or $-(4 a-12)=20$ $\Rightarrow 4 a=20+12$ or $4 a=-20+12$ $\Rightarrow a=8$ or -2 Thus, the required points on the $x$-axis are (-2,0) and $(8,0)$.Show Answer
(i) $15 x+8 y-34=0$ and $15 x+8 y+31=0 \quad$ (ii) $l(x+y)+p=0$ and $l(x+y)-r=0$.
Answer : It is known that the distance (d) between parallel lines $A x+B y+C_1=0$ and $A x+B y+C_2=0$ is given by $d=\frac{|C_1-C_2|}{\sqrt{A^{2}+B^{2}}}$ (i) The given parallel lines are $15 x+8 y$ âe" $34=0$ and $15 x+8 y+31=0$. Here, $A=15, B=8, C_1=$ - 34 , and $C_2=31$. Therefore, the distance between the parallel lines is
$d=\frac{|C_1-C_2|}{\sqrt{A^{2}+B^{2}}}=\frac{|-34-31|}{\sqrt{(15)^{2}+(8)^{2}}}$ units $=\frac{|-65|}{17}$ units $=\frac{65}{17}$ units (ii) The given parallel lines are $I(x+y)+p=0$ and $I(x+y) - r=0$. $l x+l y+p=0$ and $l x+l y - r=0$ Here, $A=I, B=I, C_1=p$, and $C_2=- r$. Therefore, the distance between the parallel lines is $d=\frac{|C_1-C_2|}{\sqrt{A^{2}+B^{2}}}=\frac{|p+r|}{\sqrt{l^{2}+l^{2}}}$ units $=\frac{|p+r|}{\sqrt{2 l^{2}}}$ units $=\frac{|p+r|}{l \sqrt{2}}$ units $=\frac{1}{\sqrt{2}}|\frac{p+r}{l}|$ unitsShow Answer
Answer : The equation of the given line is $3 x-4 y+2=0$ or $y=\frac{3 x}{4}+\frac{2}{4}$ or $y=\frac{3}{4} x+\frac{1}{2}$, which is of the form $y=m x+c$ $\therefore$ Slope of the given line $
=\frac{3}{4}
$ It is known that parallel lines have the same slope. $\therefore$ Slope of the other line $=$ $
m=\frac{3}{4}
$ Now, the equation of the line that has a slope of $\frac{3}{4}$ and passes through the point $(-$ $2,3)$ is $
\begin{aligned}
& (y-3)=\frac{3}{4}{x-(-2)} \\
& 4 y-12=3 x+6 \\
& \text{ i.e., } 3 x-4 y+18=0
\end{aligned}
$Show Answer
Answer : The given equation of line is $x-7 y+5=0$. Or, $y=\frac{1}{7} x+\frac{5}{7}$, which is of the form $y=m x+c$ $\therefore$ Slope of the given line $
=\frac{1}{7}
$ The slope of the line perpendicular to the line having a slope of $\frac{1}{7}$ is $m=-\frac{1}{(\frac{1}{7})}=-7$ The equation of the line with slope $- 7$ and $x$-intercept 3 is given by $y=m(x - d)$ $\Rightarrow y=- 7(x - 3)$ $\Rightarrow y=- 7 x+21$ $\Rightarrow 7 x+y=21$Show Answer
Answer : The given lines are $\sqrt{3} x+y=1$ and $x+\sqrt{3} y=1$. $y=-\sqrt{3} x+1 \quad \ldots(1) \quad$ and $y=-\frac{1}{\sqrt{3}} x+\frac{1}{\sqrt{3}}$ The slope of line (1) is $m_1=-\sqrt{3}$, while the slope of line (2) is $m_2=-\frac{1}{\sqrt{3}}$. The acute angle i.e., $\theta$ between the two lines is given by
$\tan \theta=|\frac{m_1-m_2}{1+m_1 m_2}|$ $\tan \theta=|\frac{-\sqrt{3}+\frac{1}{\sqrt{3}}}{1+(-\sqrt{3})(-\frac{1}{\sqrt{3}})}|$ $\tan \theta=|\frac{\frac{-3+1}{\sqrt{3}}}{1+1}|=|\frac{-2}{2 \times \sqrt{3}}|$ $\tan \theta=\frac{1}{\sqrt{3}}$ $\theta=30^{\circ}$ Thus, the angle between the given lines is either $30^{\circ}$ or $180^{\circ} - 30^{\circ}=150^{\circ}$.Show Answer
Answer : The slope of the line passing through points $(h, 3)$ and $(4,1)$ is $m_1=\frac{1-3}{4-h}=\frac{-2}{4-h}$ The slope of line $7 x$ - $9 y$ - $19=0$ or $y=\frac{7}{9} x-\frac{19}{9} \quad m_2=\frac{7}{9}$. It is given that the two lines are perpendicular. $\therefore m_1 \times m_2=-1$ $\Rightarrow(\frac{-2}{4-h}) \times(\frac{7}{9})=-1$ $\Rightarrow \frac{-14}{36-9 h}=-1$ $\Rightarrow 14=36-9 h$ $\Rightarrow 9 h=36-14$ $\Rightarrow h=\frac{22}{9}$ Thus, the value of $h$ is $\frac{22}{9}$.Show Answer
$ A(x-x_1)+B(y-y_1)=0 . $
Answer : The slope of line $A x+B y+C=0$ or $y=(\frac{-A}{B}) x+(\frac{-C}{B})$ is $\quad m=-\frac{A}{B}$ It is known that parallel lines have the same slope. $\therefore$ Slope of the other line $=m=-\frac{A}{B}$ The equation of the line passing through point $(x_1, y_1)$ and having a slope $m=-\frac{A}{B}$ is $y-y_1=m(x-x_1)$ $y-y_1=-\frac{A}{B}(x-x_1)$ $B(y-y_1)=-A(x-x_1)$ $A(x-x_1)+B(y-y_1)=0$ Hence, the line through point $(x_1, y_1)$ and parallel to line $A x+B y+C=0$ is $A(x - x_1)+B(y - y_1)=0$Show Answer
Answer : It is given that the slope of the first line, $m_1=2$. Let the slope of the other line be $m_2$. The angle between the two lines is $60^{\circ}$.
$\therefore \tan 60^{\circ}=|\frac{m_1-m_2}{1+m_1 m_2}|$ $\Rightarrow \sqrt{3}=|\frac{2-m_2}{1+2 m_2}|$ $\Rightarrow \sqrt{3}= \pm(\frac{2-m_2}{1+2 m_2})$ $\Rightarrow \sqrt{3}=\frac{2-m_2}{1+2 m_2}$ or $\sqrt{3}=-(\frac{2-m_2}{1+2 m_2})$ $\Rightarrow \sqrt{3}(1+2 m_2)=2-m_2$ or $\sqrt{3}(1+2 m_2)=-(2-m_2)$ $\Rightarrow \sqrt{3}+2 \sqrt{3} m_2+m_2=2$ or $\sqrt{3}+2 \sqrt{3} m_2-m_2=-2$ $\Rightarrow \sqrt{3}+(2 \sqrt{3}+1) m_2=2$ or $\sqrt{3}+(2 \sqrt{3}-1) m_2=-2$ $\Rightarrow m_2=\frac{2-\sqrt{3}}{(2 \sqrt{3}+1)}$ or $m_2=\frac{-(2+\sqrt{3})}{(2 \sqrt{3}-1)}$ Case I: $\quad m_2=(\frac{2-\sqrt{3}}{2 \sqrt{3}+1})$ The equation of the line passing through point $(2,3)$ and having a slope of $\frac{(2-\sqrt{3})}{(2 \sqrt{3}+1)}$ is $(y-3)=\frac{2-\sqrt{3}}{2 \sqrt{3}+1}(x-2)$ $(2 \sqrt{3}+1) y-3(2 \sqrt{3}+1)=(2-\sqrt{3}) x-2(2-\sqrt{3})$ $(\sqrt{3}-2) x+(2 \sqrt{3}+1) y=-4+2 \sqrt{3}+6 \sqrt{3}+3$ $(\sqrt{3}-2) x+(2 \sqrt{3}+1) y=-1+8 \sqrt{3}$ In this case, the equation of the other line is $(\sqrt{3}-2) x+(2 \sqrt{3}+1) y=-1+8 \sqrt{3}$. Case II : $\quad m_2=\frac{-(2+\sqrt{3})}{(2 \sqrt{3}-1)}$ The equation of the line passing through point $(2,3)$ and having a slope of $\frac{-(2+\sqrt{3})}{(2 \sqrt{3}-1)}$ is $
\begin{aligned}
& (y-3)=\frac{-(2+\sqrt{3})}{(2 \sqrt{3}-1)}(x-2) \\
& (2 \sqrt{3}-1) y-3(2 \sqrt{3}-1)=-(2+\sqrt{3}) x+2(2+\sqrt{3}) \\
& (2 \sqrt{3}-1) y+(2+\sqrt{3}) x=4+2 \sqrt{3}+6 \sqrt{3}-3 \\
& (2+\sqrt{3}) x+(2 \sqrt{3}-1) y=1+8 \sqrt{3}
\end{aligned}
$ In this case, the equation of the other line is $(2+\sqrt{3}) x+(2 \sqrt{3}-1) y=1+8 \sqrt{3}$. Thus, the required equation of the other line is $(\sqrt{3}-2) x+(2 \sqrt{3}+1) y=-1+8 \sqrt{3}$ or $(2+\sqrt{3}) x+(2 \sqrt{3}-1) y=1+8 \sqrt{3}$Show Answer
Answer : The right bisector of a line segment bisects the line segment at $90^{\circ}$. The end-points of the line segment are given as A $(3,4)$ and $B(-{ } 1,2)$. Accordingly, mid-point of $A B$ $
=(\frac{3-1}{2}, \frac{4+2}{2})=(1,3)
$ Slope of $A B=\frac{2-4}{-1-3}=\frac{-2}{-4}=\frac{1}{2}$ $\therefore$ Slope of the line perpendicular to $A B=$ $
=-\frac{1}{(\frac{1}{2})}=-2
$ The equation of the line passing through $(1,3)$ and having a slope of - 2 is (y - 3$)=$ -2 (x - 1) $y $ - $3=- 2 x+2$ $2 x+y=5$ Thus, the required equation of the line is $2 x+y=5$.Show Answer
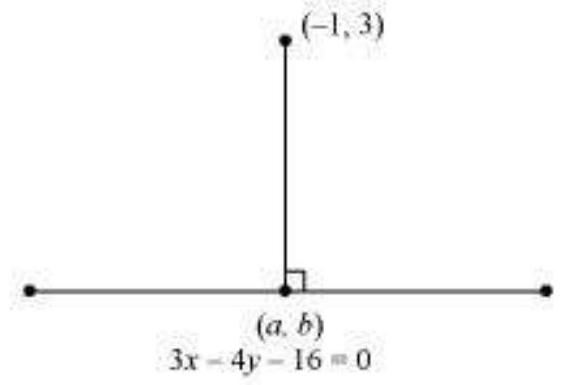
Answer : Let $(a, b)$ be the coordinates of the foot of the perpendicular from the point $(- 1,3)$ to the line $3 x - 4 y - 16=0$. Slope of the line joining $( - 1,3) \text{ and } (a, b), m_1=\frac{b-3}{a+1}$ Slope of the line $3 x$- $4 y$- $16=0$ or $y=\frac{3}{4} x-4, m_2=\frac{3}{4}$ Since these two lines are perpendicular, $m_1 m_2=$ - 1 $\therefore(\frac{b-3}{a+1}) \times(\frac{3}{4})=-1$ $\Rightarrow \frac{3 b-9}{4 a+4}=-1$ $\Rightarrow 3 b-9=-4 a-4$ $\Rightarrow 4 a+3 b=5$ Point $(a, b)$ lies on line $3 x$ - $4 y=16$. $\therefore 3 a$ - $4 b=16$ On solving equations (1) and (2), we obtain $a=\frac{68}{25}$ and $b=-\frac{49}{25}$ Thus, the required coordinates of the foot of the perpendicular are $(\frac{68}{25},-\frac{49}{25})$Show Answer
Answer : The given equation of line is $y=m x+c$. It is given that the perpendicular from the origin meets the given line at (-1,2). Therefore, the line joining the points $(0,0)$ and $(- 1,2)$ is perpendicular to the given line. $\therefore$ Slope of the line joining $(0,0)$ and $( - 1,2)$ $
=\frac{2}{-1}=-2
$ The slope of the given line is $m$. $\therefore m \times-2=-$ [The two lines are perpendicular] $\Rightarrow m=\frac{1}{2}$ Since point $( - 1,2)$ lies on the given line, it satisfies the equation $y=m x+c$. $\therefore 2=m(-1)+c$ $\Rightarrow 2=\frac{1}{2}(-1)+c$ $\Rightarrow c=2+\frac{1}{2}=\frac{5}{2}$ Thus, the respective values of $m$ and $c$ are $\frac{1}{2}$ and $\frac{5}{2}$.Show Answer
Answer : The equations of given lines are $x \cos \theta - y \sin \theta=k \cos 2 \theta \ldots$ (1) $x \sec \theta+y cosec \theta=k$. The perpendicular distance $(d)$ of a line $A x+B y+C=0$ from a point $(x_1, y_1)$ is given by $$
\begin{equation*}
d=\frac{|A x_1+B y_1+C|}{\sqrt{A^{2}+B^{2}}} . \tag{2}
\end{equation*}
$$ On comparing equation (1) to the general equation of line i.e., $A x+B y+C=0$, we obtain $A=\cos \theta, B=$ -sin $\theta$, and $C=- k \cos 2 \theta$. It is given that $p$ is the length of the perpendicular from $(0,0)$ to line (1).
$\therefore p=\frac{|A(0)+B(0)+C|}{\sqrt{A^{2}+B^{2}}}=\frac{|C|}{\sqrt{A^{2}+B^{2}}}=\frac{|-k \cos 2 \theta|}{\sqrt{\cos ^{2} \theta+\sin ^{2} \theta}}=|-k \cos 2 \theta|$ On comparing equation (2) to the general equation of line i.e., $A x+B y+C=0$, we obtain $A=\sec \theta, B=cosec \theta$, and $C=$ -k. It is given that $q$ is the length of the perpendicular from $(0,0)$ to line (2). $\therefore q=\frac{|A(0)+B(0)+C|}{\sqrt{A^{2}+B^{2}}}=\frac{|C|}{\sqrt{A^{2}+B^{2}}}=\frac{|-k|}{\sqrt{\sec ^{2} \theta+cosec^{2} \theta}}$ From (3) and (4), we have $
\begin{aligned}
& p^{2}+4 q^{2}=(\mid-k \cos 2 \theta)^{2}+4(\frac{|-k|}{\sqrt{\sec ^{2} \theta+cosec^{2} \theta}})^{2} \\
& =k^{2} \cos ^{2} 2 \theta+\frac{4 k^{2}}{(\sec ^{2} \theta+cosec^{2} \theta)} \\
& =k^{2} \cos ^{2} 2 \theta+\frac{4 k^{2}}{(\frac{1}{\cos ^{2} \theta}+\frac{1}{\sin ^{2} \theta})} \\
& =k^{2} \cos ^{2} 2 \theta+\frac{4 k^{2}}{(\frac{\sin ^{2} \theta+\cos ^{2} \theta}{\sin ^{2} \theta \cos ^{2} \theta})} \\
& =k^{2} \cos ^{2} 2 \theta+\frac{4 k^{2}}{(\frac{1}{\sin ^{2} \theta \cos ^{2} \theta})} \\
& =k^{2} \cos ^{2} 2 \theta+4 k^{2} \sin ^{2} \theta \cos ^{2} \theta \\
& =k^{2} \cos ^{2} 2 \theta+k^{2}(2 \sin ^{2} \theta \cos ^{2} \theta. \\
& =k^{2} \cos ^{2} 2 \theta+k^{2} \sin ^{2} 2 \theta \\
& =k^{2}(\cos ^{2} 2 \theta+\sin ^{2} 2 \theta) \\
& =k^{2}
\end{aligned}
$ Hence, we proved that $p^{2}+4 q^{2}=k^{2}$.Show Answer
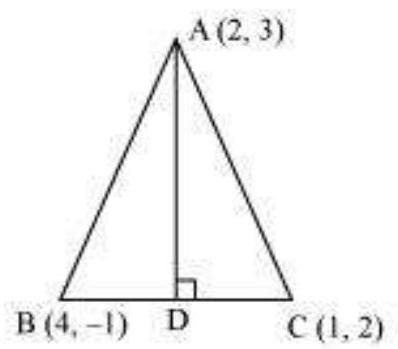
Answer : Let $A D$ be the altitude of triangle $A B C$ from vertex $A$. Accordingly, $A D \perp B C$ The equation of the line passing through point $(2,3)$ and having a slope of 1 is $(y - 3)=1(x -2 )$ $\Rightarrow x - y+1=0$ $\Rightarrow y $ - $x=1$ Therefore, equation of the altitude from vertex $A=y $ - $x=1$. Length of $A D=$ Length of the perpendicular from $A(2,3)$ to $B C$ The equation of $B C$ is $(y+1)=\frac{2+1}{1-4}(x-4)$ $\Rightarrow(y+1)=-1(x-4)$ $\Rightarrow y+1=-x+4$ $\Rightarrow x+y-3=0$ The perpendicular distance $(d)$ of a line $A x+B y+C=0$ from a point $(x_1, y_1)$ is given by $\sqrt{A^{2}+B^{2}}$. On comparing equation (1) to the general equation of line $A x+B y+C=0$, we obtain $A=1, B=1$, and $C=$ - 3 . $\therefore$ Length of $A D$ $
=\frac{|1 \times 2+1 \times 3-3|}{\sqrt{1^{2}+1^{2}}} \text{ units }=\frac{|2|}{\sqrt{2}} \text{ units }=\frac{2}{\sqrt{2}} \text{ units }=\sqrt{2} \text{ units }
$ Thus, the equation and the length of the altitude from vertex $A$ are $y -$ $x=1$ and $\sqrt{2}$ units respectively.Show Answer
Show Answer
Answer :
It is known that the equation of a line whose intercepts on the axes are $a$ and $b$ is
$$ \begin{align*} & \frac{x}{a}+\frac{y}{b}=1 \\ & \text{ or } b x+a y=a b \\ & \text{ or } b x+a y-a b=0 \tag{1} \end{align*} $$
The perpendicular distance $(d)$ of a line $A x+B y+C=0$ from a point $(x_1, y_1)$ is given by
$ d=\frac{|A x_1+B y_1+C|}{\sqrt{A^{2}+B^{2}}} $
On comparing equation (1) to the general equation of line $A x+B y+C=0$, we obtain $A=b, B=a$, and $C=a -a b$.
Therefore, if $p$ is the length of the perpendicular from point $(x_1, y_1)=(0,0)$ to line (1), we obtain
$p=\frac{|A(0)+B(0)-a b|}{\sqrt{b^{2}+a^{2}}}$
$\Rightarrow p=\frac{|-a b|}{\sqrt{a^{2}+b^{2}}}$
On squaring both sides, we obtain
$p^{2}=\frac{(-a b)^{2}}{a^{2}+b^{2}}$
$\Rightarrow p^{2}(a^{2}+b^{2})=a^{2} b^{2}$
$\Rightarrow \frac{a^{2}+b^{2}}{a^{2} b^{2}}=\frac{1}{p^{2}}$
$\Rightarrow \frac{1}{p^{2}}=\frac{1}{a^{2}}+\frac{1}{b^{2}}$
Hence, we showed that $\frac{1}{p^{2}}=\frac{1}{a^{2}}+\frac{1}{b^{2}}$.
Miscellaneous Examples
Example 11 If the lines $2 x+y-3=0,5 x+k y-3=0$ and $3 x-y-2=0$ are concurrent, find the value of $k$.
Solution Three lines are said to be concurrent, if they pass through a common point, i.e., point of intersection of any two lines lies on the third line. Here given lines are
$ \begin{aligned} & 2 x+y-3=0 \quad \quad\quad\quad\quad\quad\quad\quad\ldots(1) \\ & 5 x+k y-3=0 \quad \quad\quad\quad\quad\quad\quad\quad\ldots(2) \\ & 3 x-y-2=0 \quad \quad\quad\quad\quad\quad\quad\quad\ldots(3) \end{aligned} $
Solving (1) and (3) by cross-multiplication method, we get
$ \frac{x}{-2-3}=\frac{y}{-9+4}=\frac{1}{-2-3} \quad \text{ or } \quad x=1, y=1 \text{. } $
Therefore, the point of intersection of two lines is $(1,1)$. Since above three lines are concurrent, the point $(1,1)$ will satisfy equation $(2)$ so that
$ 5.1+k .1-3=0 \text{ or } k=-2 \text{. } $
Example 12 Find the distance of the line $4 x-y=0$ from the point $P(4,1)$ measured along the line making an angle of $135^{\circ}$ with the positive $x$-axis.
Solution Given line is $4 x-y=0 \quad \quad\quad\quad\quad\quad\quad\quad\ldots(1)$
In order to find the distance of the line (1) from the point $P(4,1)$ along another line, we have to find the point of intersection of both the lines. For this purpose, we will first find the equation of the second line (Fig 9.16). Slope of second line is $\tan 135^{\circ}=-1$. Equation of the line with slope -1 through the point $P(4,1)$ is

$ y-1=-1(x-4) \text{ or } x+y-5=0 \quad \quad\quad\quad\quad\quad\quad\quad\ldots(2) $
Solving (1) and (2), we get $x=1$ and $y=4$ so that point of intersection of the two lines is $Q(1,4)$. Now, distance of line (1) from the point $P(4,1)$ along the line (2) $=$ the distance between the points $P(4,1)$ and $Q(1,4)$.
$ =\sqrt{(1-4)^{2}+(4-1)^{2}}=3 \sqrt{2} \text{ units. } $
Example 13 Assuming that straight lines work as the plane mirror for a point, find the image of the point $(1,2)$ in the line $x-3 y+4=0$.
Solution Let $Q(h, k)$ is the image of the point $P(1,2)$ in the line
$ x-3 y+4=0 \quad \quad\quad\quad\quad\quad\quad\quad\ldots(1) $
Therefore, the line (1) is the perpendicular bisector of line segment PQ (Fig 9.17).

Hence Slope of line $PQ=\frac{-1}{\text{ Slope of line } x-3 y+4=0}$,
so that $\frac{k-2}{h-1}=\frac{-1}{\frac{1}{3}} \quad$ or $\quad 3 h+k=5\quad \quad\quad\quad\quad\ldots(2)$
and the mid-point of $PQ$, i.e., point $(\frac{h+1}{2}, \frac{k+2}{2})$ will satisfy the equation (1) so that
$ \frac{h+1}{2}-3(\frac{k+2}{2})+4=0 \text{ or } h-3 k=-3 \quad \quad\quad\quad\quad\ldots(3) $
Solving (2) and (3), we get $h=\frac{6}{5}$ and $k=\frac{7}{5}$.
Hence, the image of the point $(1,2)$ in the line (1) is $(\frac{6}{5}, \frac{7}{5})$.
Example 14 Show that the area of the triangle formed by the lines
$y=m_1 x+c_1, y=m_2 x+c_2$ and $x=0$ is $\frac{(c_1-c_2)^{2}}{2|m_1-m_2|}$.
Solution Given lines are
$y=m_1 x+c_1 \quad \quad\quad\quad\quad\ldots(1)$
$y=m_2 x+c_2\quad \quad\quad\quad\quad\ldots(2)$
$x=0\quad \quad\quad\quad\quad\quad\quad\quad\ldots(3)$
We know that line $y=m x+c$ meets the line $x=0$ ( $y$-axis) at the point $(0, c)$. Therefore, two vertices of the triangle formed by lines (1) to (3) are $P(0, c_1)$ and $Q(0, c_2)$ (Fig 9.18).

Third vertex can be obtained by solving equations (1) and (2). Solving (1) and (2), we get
$ x=\frac{(c_2-c_1)}{(m_1-m_2)} \text{ and } y=\frac{(m_1 c_2-m_2 c_1)}{(m_1-m_2)} $
Therefore, third vertex of the triangle is $R(\frac{(c_2-c_1)}{(m_1-m_2)}, \frac{(m_1 c_2-m_2 c_1)}{(m_1-m_2)})$.
Now, the area of the triangle is
$ =\frac{1}{2}|0(\frac{m_1 c_2-m_2 c_1}{m_1-m_2}-c_2)+\frac{c_2-c_1}{m_1-m_2}(c_2-c_1)+0(c_1-\frac{m_1 c_2-m_2 c_1}{m_1-m_2})|=\frac{(c_2-c_1)^{2}}{2|m_1-m_2|} $
Example 15 A line is such that its segment between the lines
$5 x-y+4=0$ and $3 x+4 y-4=0$ is bisected at the point $(1,5)$. Obtain its equation.
Solution Given lines are
$5 x-y+4=0 \quad \quad \quad \quad \quad \quad \quad \ldots (1)$
$3 x+4 y-4=0 \quad \quad \quad \quad \quad \quad \quad \ldots(2)$
Let the required line intersects the lines (1) and (2) at the points, $(\alpha_1, \beta_1)$ and $(\alpha_2, \beta_2)$, respectively (Fig 9.19). Therefore

$ \begin{aligned} & 5 \alpha_1-\beta_1+4=0 \text{ and } \\ & 3 \alpha_2+4 \beta_2-4=0 \end{aligned} $
or $\beta_1=5 \alpha_1+4$ and $\beta_2=\frac{4-3 \alpha_2}{4}$.
We are given that the mid point of the segment of the required line between $(\alpha_1, \beta_1)$ and $(\alpha_2, \beta_2)$ is $(1,5)$. Therefore
$ \frac{\alpha_1+\alpha_2}{2}=1 \text{ and } \frac{\beta_1+\beta_2}{2}=5 \text{, } $
or
$ \begin{aligned} & \alpha_1+\alpha_2=2 \text{ and } \frac{5 \alpha_1+4+\frac{4-3 \alpha_2}{4}}{2}=5 \text{, } \\ & \text{ or } \alpha_1+\alpha_2=2 \text{ and } 20 \alpha_1-3 \alpha_2=20 \quad \quad \quad \quad \quad \ldots (3) \end{aligned} $
Solving equations in (3) for $\alpha_1$ and $\alpha_2$, we get
$ \alpha_1=\frac{26}{23} \text{ and } \alpha_2=\frac{20}{23} \text{ and hence, } \beta_1=5 \cdot \frac{26}{23}+4=\frac{222}{23} \text{. } $
Equation of the required line passing through $(1,5)$ and $(\alpha_1, \beta_1)$ is
$ y-5=\frac{\beta_1-5}{\alpha_1-1}(x-1) \text{ or } y-5=\frac{\frac{222}{23}-5}{\frac{26}{23}-1}(x-1) $
or $ \quad \quad \quad \quad \quad \quad \quad 107 x-3 y-92=0 $
which is the equation of required line.
Example 16 Show that the path of a moving point such that its distances from two lines $3 x-2 y=5$ and $3 x+2 y=5$ are equal is a straight line.
Solution Given lines are
$ \begin{aligned} & \quad\quad \quad 3 x-2 y=5 \quad\quad\quad\quad\quad\quad\quad\quad \ldots (1)\\ & \text{ and } \quad 3 x+2 y=5 \quad\quad\quad\quad\quad\quad\quad\quad \ldots(2) \end{aligned} $
Let $(h, k)$ is any point, whose distances from the lines (1) and (2) are equal. Therefore
$ \frac{|3 h-2 k-5|}{\sqrt{9+4}}=\frac{|3 h+2 k-5|}{\sqrt{9+4}} \text{ or }|3 h-2 k-5|=|3 h+2 k-5|, $
which gives $3 h-2 k-5=3 h+2 k-5$ or $-(3 h-2 k-5)=3 h+2 k-5$.
Solving these two relations we get $k=0$ or $h=\frac{5}{3}$. Thus, the point $(h, k)$ satisfies the equations $y=0$ or $x=\frac{5}{3}$, which represent straight lines. Hence, path of the point equidistant from the lines (1) and (2) is a straight line.
Miscellaneous Exercise on Chapter 9
1. Find the values of $k$ for which the line $(k-3) x-(4-k^{2}) y+k^{2}-7 k+6=0$ is
(a) Parallel to the $x$-axis,
(b) Parallel to the $y$-axis,
(c) Passing through the origin.
Answer : The given equation of line is (k - 3) x - $(4 - k^{2}) y+k^{2} $ -$7 k+6=0$ (a) If the given line is parallel to the $x$-axis, then Slope of the given line $=$ Slope of the $x$-axis The given line can be written as ( 4 - $ k^{2}) y=(k $ -3 $) x+k^{2}- 7 k+6=0$ $y=\frac{(k-3)}{(4-k^{2})} x+\frac{k^{2}-7 k+6}{(4-k^{2})}$ , which is of the form $y=m x+c$. $\therefore$ Slope of the given line $=\frac{(k-3)}{(4-k^{2})}$ Slope of the $x$-axis $=0$ $\therefore \frac{(k-3)}{(4-k^{2})}=0$ $\Rightarrow k-3=0$ $\Rightarrow k=3$ Thus, if the given line is parallel to the $x$-axis, then the value of $k$ is 3 . (b) If the given line is parallel to the $y$-axis, it is vertical. Hence, its slope will be undefined. The slope of the given line is $\frac{(k-3)}{(4-k^{2})}$. Now, $\frac{(k-3)}{(4-k^{2})}$ is undefined at $k^{2}=4$ $k^{2}=4$ $\Rightarrow k= \pm 2$ Thus, if the given line is parallel to the $y$-axis, then the value of $k$ is $\pm 2$. (c) If the given line is passing through the origin, then point $(0,0)$ satisfies the given equation of line. $(k-3)(0)-(4-k^{2})(0)+k^{2}-7 k+6=0$ $k^{2}-7 k+6=0$ $k^{2}-6 k-k+6=0$ $(k-6)(k-1)=0$ $k=1$ or 6 Thus, if the given line is passing through the origin, then the value of $k$ is either 1 or 6 . Answer : Let the intercepts cut by the given lines on the axes be $a$ and $b$. It is given that $a+b=1 \ldots(1)$ $a b=- 6$ On solving equations (1) and (2), we obtain $a=3$ and $b=$ - 2 or $a=-2$ and $b=3$ It is known that the equation of the line whose intercepts on the axes are $a$ and $b$ is $\frac{x}{a}+\frac{y}{b}=1$ or $b x+a y-a b=0$ Case I: $a=3$ and $b=$ - 2 In this case, the equation of the line is - $2 x+3 y+6=0$, i.e., $2 x$ - $3 y=6$. Case II: $a=$ - 2 and $b=3$ In this case, the equation of the line is $3 x $ - $2 y+6=0$, i.e., - $3 x+2 y=6$. Thus, the required equation of the lines are $2 x $ - $3 y=6$ and $-3 x+2 y=6$. Answer : Let $(0, b)$ be the point on the $y$-axis whose distance from line $\frac{x}{3}+\frac{y}{4}=1$ is 4 units. The given line can be written as $4 x+3 y$ - $12=0$ On comparing equation (1) to the general equation of line $A x+B y+C=0$, we obtain $A=4, B=3$, and $C=\hat{a} \ell^{\text{" }} 12$. It is known that the perpendicular distance $(d)$ of a line $A x+B y+C=0$ from a point $(x_1, y_1)$ is given by $d=\frac{|A x_1+B y_1+C|}{\sqrt{A^{2}+B^{2}}}$. Therefore, if $(0, b)$ is the point on the $y$-axis whose distance from line $\frac{x}{3}+\frac{y}{4}=1$ is 4 units, then:
$4=\frac{|4(0)+3(b)-12|}{\sqrt{4^{2}+3^{2}}}$ $\Rightarrow 4=\frac{|3 b-12|}{5}$ $\Rightarrow 20=|3 b-12|$ $\Rightarrow 20= \pm(3 b-12)$ $\Rightarrow 20=(3 b-12)$ or $20=-(3 b-12)$ $\Rightarrow 3 b=20+12$ or $3 b=-20+12$ $\Rightarrow b=\frac{32}{3}$ or $b=-\frac{8}{3}$ Thus, the required points are $(0, \frac{32}{3})$ and $(0,-\frac{8}{3})$. Answer : The equation of the line joining the points $(\cos \theta, \sin \theta)$ and $(\cos \phi, \sin \phi)$ is given by $
\begin{aligned}
& y-\sin \theta=\frac{\sin \phi-\sin \theta}{\cos \phi-\cos \theta}(x-\cos \theta) \\
& y(\cos \phi-\cos \theta)-\sin \theta(\cos \phi-\cos \theta)=x(\sin \phi-\sin \theta)-\cos \theta(\sin \phi-\sin \theta) \\
& x(\sin \theta-\sin \phi)+y(\cos \phi-\cos \theta)+\cos \theta \sin \phi-\cos \theta \sin \theta-\sin \theta \cos \phi+\sin \theta \cos \theta=0 \\
& x(\sin \theta-\sin \phi)+y(\cos \phi-\cos \theta)+\sin (\phi-\theta)=0 \\
& A x+B y+C=0, \text{ where } A=\sin \theta-\sin \phi, B=\cos \phi-\cos \theta, \text{ and } C=\sin (\phi-\theta)
\end{aligned}
$ It is known that the perpendicular distance $(d)$ of a line $A x+B y+C=0$ from a point $(x_1, y_1)$ is given by $d=\frac{|A x_1+B y_1+C|}{\sqrt{A^{2}+B^{2}}}$. Therefore, the perpendicular distance $(d)$ of the given line from point $(x_1, y_1)=(0,0)$ is $
\begin{aligned}
& d=\frac{|(\sin \theta-\sin \phi)(0)+(\cos \phi-\cos \theta)(0)+\sin (\phi-\theta)|}{\sqrt{(\sin \theta-\sin \phi)^{2}+(\cos \phi-\cos \theta)^{2}}} \\
& =\frac{|\sin (\phi-\theta)|}{\sqrt{\sin ^{2} \theta+\sin ^{2} \phi-2 \sin \theta \sin \phi+\cos ^{2} \phi+\cos ^{2} \theta-2 \cos \phi \cos \theta}} \\
& =\frac{|\sin (\phi-\theta)|}{\sqrt{(\sin ^{2} \theta+\cos ^{2} \theta)+(\sin ^{2} \phi+\cos ^{2} \phi)-2(\sin \theta \sin \phi+\cos \theta \cos \phi)}} \\
& =\frac{|\sin (\phi-\theta)|}{\sqrt{1+1-2(\cos (\phi-\theta))}} \\
& =\frac{|\sin (\phi-\theta)|}{\sqrt{2(1-\cos (\phi-\theta))}} \\
& =\frac{|\sin (\phi-\theta)|}{\sqrt{2(2 \sin ^{2}(\frac{\phi-\theta}{2}))}} \\
& =\frac{|\sin (\phi-\theta)|}{|2 \sin (\frac{\phi-\theta}{2})|}
\end{aligned}
$ Answer : The equation of any line parallel to the $y$-axis is of the form $x=a$ The two given lines are $x$ - $7 y+5=0$ $3 x+y=0$ On solving equations (2) and (3), we obtain $x=-\frac{5}{22}$ and $y=\frac{15}{22}$. Therefore, $(-\frac{5}{22}, \frac{15}{22})$ is the point of intersection of lines (2) and (3). Since line $x=a$ passes through point $(-\frac{5}{22}, \frac{15}{22}), a=-\frac{5}{22}$. Thus, the required equation of the line is $x=-\frac{5}{22}$. Answer : The equation of the given line is $\frac{x}{4}+\frac{y}{6}=1$. This equation can also be written as $3 x+2 y$ âє“ $12=0$ $y=\frac{-3}{2} x+6$ , which is of the form $y=m x+c$ $\therefore$ Slope of the given line $=-\frac{3}{2}$ $\therefore$ Slope of line perpendicular to the given line $
=-\frac{1}{(-\frac{3}{2})}=\frac{2}{3}
$ Let the given line intersect the $y$-axis at $(0, y)$. On substituting $x$ with 0 in the equation of the given line, we obtain $\frac{y}{6}=1 \Rightarrow y=6$ $\therefore$ The given line intersects the $y$-axis at $(0,6)$. The equation of the line that has a slope of $\frac{2}{3}$ and passes through point $(0,6)$ is $(y-6)=\frac{2}{3}(x-0)$ $3 y-18=2 x$ $2 x-3 y+18=0$ Thus, the required equation of the line is $2 x-3 y+18=0$. Answer : The equations of the given lines are $y$ - $x=0$ $x+y=0$. $x$ - $k=0$ The point of intersection of lines (1) and (2) is given by $x=0$ and $y=0$ The point of intersection of lines (2) and (3) is given by $x=k$ and $y=$ -k The point of intersection of lines (3) and (1) is given by $x=k$ and $y=k$ Thus, the vertices of the triangle formed by the three given lines are $(0,0),(k, -k) $, and $(k, k)$. We know that the area of a triangle whose vertices are $(x_1, y_1),(x_2, y_2)$, and $(x_3, y_3)$ is $\frac{1}{2}|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)|$ Therefore, area of the triangle formed by the three given lines $=\frac{1}{2}|0(-k-k)+k(k-0)+k(0+k)|$ square units $=\frac{1}{2}|k^{2}+k^{2}|$ square units $=\frac{1}{2}|2 k^{2}|$ square units $=k^{2}$ square units Answer : The equations of the given lines are $3 x+y-2=0$ $p x+2 y-3=0$
$2 x-y-3=0$… On solving equations (1) and (3), we obtain $x=1$ and $y=-1$ Since these three lines may intersect at one point, the point of intersection of lines (1) and (3) will also satisfy line (2). $p(1)+2(-1)-3=0$ $p-2-3=0$ $p=5$ Thus, the required value of $p$ is 5 . Answer : The equations of the given lines are $y=m_1 x+c_1 \ldots(1)$ $y=m_2 x+c_2 \ldots$ $y=m_3 x+c_3$. On subtracting equation (1) from (2), we obtain $0=(m_2-m_1) x+(c_2-c_1)$ $\Rightarrow(m_1-m_2) x=c_2-c_1$ $\Rightarrow x=\frac{c_2-c_1}{m_1-m_2}$ On substituting this value of $x$ in (1), we obtain $
\begin{aligned}
& y=m_1(\frac{c_2-c_1}{m_1-m_2})+c_1 \\
& y=\frac{m_1 c_2-m_1 c_1}{m_1-m_2}+c_1 \\
& y=\frac{m_1 c_2-m_1 c_1+m_1 c_1-m_2 c_1}{m_1-m_2} \\
& y=\frac{m_1 c_2-m_2 c_1}{m_1-m_2}
\end{aligned}
$ $
\therefore(\frac{c_2-c_1}{m_1-m_2}, \frac{m_1 c_2-m_2 c_1}{m_1-m_2}) \text{ is the point of intersection of lines (1) and (2). }
$ It is given that lines (1), (2), and (3) are concurrent. Hence, the point of intersection of lines (1) and (2) will also satisfy equation (3). $
\begin{aligned}
& \frac{m_1 c_2-m_2 c_1}{m_1-m_2}=m_3(\frac{c_2-c_1}{m_1-m_2})+c_3 \\
& \frac{m_1 c_2-m_2 c_1}{m_1-m_2}=\frac{m_3 c_2-m_3 c_1+c_3 m_1-c_3 m_2}{m_1-m_2} \\
& m_1 c_2-m_2 c_1-m_3 c_2+m_3 c_1-c_3 m_1+c_3 m_2=0 \\
& m_1(c_2-c_3)+m_2(c_3-c_1)+m_3(c_1-c_2)=0 \\
& \text{ Hence, } m_1(c_2-c_3)+m_2(c_3-c_1)+m_3(c_1-c_2)=0 .
\end{aligned}
$ Answer : Let the slope of the required line be $m_1$. The given line can be written as $y=\frac{1}{2} x-\frac{3}{2}$, which is of the form $y=m x+c$ $\therefore$ Slope of the given line $=m_2=\frac{1}{2}$ It is given that the angle between the required line and line $x - 2 y=3$ is $45^{\circ}$. We know that if $\theta$ isthe acute angle between lines $I_1$ and $I_2$ with slopes $m_1$ and $m_2$ respectively, then $\tan \theta=|\frac{m_2-m_1}{1+m_1 m_2}|$
$\therefore \tan 45^{\circ}=\frac{|m_1-m_2|}{1+m_1 m_2}$ $\Rightarrow I=|\frac{\frac{1}{2}-m_1}{1+\frac{m_1}{2}}|$ $\Rightarrow 1=|\frac{(\frac{1-2 m_1}{2})}{\frac{2+m_1}{2}}|$ $\Rightarrow 1=|\frac{1-2 m_1}{2+m_1}|$ $\Rightarrow 1= \pm(\frac{1-2 m_1}{2+m_1})$ $\Rightarrow 1=\frac{1-2 m_1}{2+m_1}$ or $1=-(\frac{1-2 m_1}{2+m_1})$ $\Rightarrow 2+m_1=1-2 m_1$ or $2+m_1=-1+2 m_1$ $\Rightarrow m_1=-\frac{1}{3}$ or $m_1=3$ Case I: $m_1=3$ The equation of the line passing through $(3,2)$ and having a slope of 3 is: $y$ - 2 = $3(x$ - 3 $)$ $y$ - $2=3 x$ - 9 $3 x -y=7$ Case II: $m_1=-\frac{1}{3}$ The equation of the line passing through $(3,2)$ and having a slope of $-\frac{1}{3}$ is: $y-2=-\frac{1}{3}(x-3)$ $3 y-6=-x+3$ $x+3 y=9$ Thus, the equations of the lines are $3 x$ - $y=7$ and $x+3 y=9$. Answer : Let the equation of the line having equal intercepts on the axes be $\frac{x}{a}+\frac{y}{a}=1$ Or $x+y=a$ On solving equations $4 x+7 y - 3=0$ and $2 x $ - $3 y+1=0$, we obtain $x=\frac{1}{13}$ and $y=\frac{5}{13}$. $\therefore(\frac{1}{13}, \frac{5}{13})$ is the point of intersection of the two given lines. Since equation (1) passes through point $(\frac{1}{13}, \frac{5}{13})$, $\frac{1}{13}+\frac{5}{13}=a$ $\Rightarrow a=\frac{6}{13}$ $\therefore$ Equation (1) becomes $
x+y=\frac{6}{13} \text{, i.e., } 13 x+13 y=6
$ Thus, the required equation of the line is $13 x+13 y=6$ $\theta$ with the line $y=m x+c$ is $\frac{y}{x}=\frac{m \pm \tan ,}{1 \mp m \tan ,}$. Answer : Let the equation of the line passing through the origin be $y=m_1 x$. If this line makes an angle of $\theta$ with line $y=m x+c$, then angle $\theta$ is given by
$\therefore \tan \theta=|\frac{m_1-m}{1+m_1 m}|$ $\Rightarrow \tan \theta=|\frac{\frac{y}{x}-m}{1+\frac{y}{x} m}|$ $\Rightarrow \tan \theta= \pm(\frac{\frac{y}{x}-m}{1+\frac{y}{x} m})$ $\Rightarrow \tan \theta=\frac{\frac{y}{x}-m}{1+\frac{y}{x} m}$ or $\tan \theta=-(\frac{\frac{y}{x}-m}{1+\frac{y}{x} m})$ Case I: $\quad \tan \theta=\frac{\frac{y}{x}-m}{1+\frac{y}{x} m}$ $
\tan \theta=\frac{\frac{y}{x}-m}{1+\frac{y}{x} m}
$ $\Rightarrow \tan \theta+\frac{y}{x} m \tan \theta=\frac{y}{x}-m$ $\Rightarrow m+\tan \theta=\frac{y}{x}(1-m \tan \theta)$ $\Rightarrow \frac{y}{x}=\frac{m+\tan \theta}{1-m \tan \theta}$ Case II: $
\tan \theta=-(\frac{\frac{y}{x}-m}{1+\frac{y}{x} m})
$ $\tan \theta=-(\frac{\frac{y}{x}-m}{1+\frac{y}{x} m})$ $\Rightarrow \tan \theta+\frac{y}{x} m \tan \theta=-\frac{y}{x}+m$ $\Rightarrow \frac{y}{x}(1+m \tan \theta)=m-\tan \theta$ $\Rightarrow \frac{y}{x}=\frac{m-\tan \theta}{1+m \tan \theta}$ Therefore, the required line is given by $\frac{y}{x}=\frac{m \pm \tan \theta}{1 \mp m \tan \theta}$ Answer : The equation of the line joining the points ( $.-{ }^{*} 1,1)$ and $(5,7)$ is given by $y-1=\frac{7-1}{5+1}(x+1)$ $y-1=\frac{6}{6}(x+1)$ $x-y+2=0$ The equation of the given line is $x+y-=0$… The point of intersection of lines (1) and (2) is given by $x=1$ and $y=3$ Let point $(1,3)$ divide the line segment joining $(- 1,1)$ and $(5,7)$ in the ratio $1: k$. Accordingly, by section formula,
$(1,3)=(\frac{k(-1)+1(5)}{1+k}, \frac{k(1)+1(7)}{1+k})$ $\Rightarrow(1,3)=(\frac{-k+5}{1+k}, \frac{k+7}{1+k})$ $\Rightarrow \frac{-k+5}{1+k}=1, \frac{k+7}{1+k}=3$ $\therefore \frac{-k+5}{1+k}=1$ $\Rightarrow-k+5=1+k$ $\Rightarrow 2 k=4$ $\Rightarrow k=2$ Thus, the line joining the points ( $-$ “ 1,1$)$ and $(5,7)$ is divided by line $x+y=4$ in the ratio $1: 2$. Answer : The given lines are $2 x - y=0$… $4 x+7 y+5=0 \ldots$ A $(1,2)$ is a point on line (1). Let $B$ be the point of intersection of lines (1) and (2). On solving equations (1) and (2), we obtain $
x=\frac{-5}{18} \text{ and } y=\frac{-5}{9}
$ $\therefore$ Coordinates of point $B$ are $(\frac{-5}{18}, \frac{-5}{9})$. By using distance formula, the distance between points $A$ and $B$ can be obtained as $AB=\sqrt{(1+\frac{5}{18})^{2}+(2+\frac{5}{9})^{2}}$ units $=\sqrt{(\frac{23}{18})^{2}+(\frac{23}{9})^{2}}$ units $=\sqrt{(\frac{23}{2 \times 9})^{2}+(\frac{23}{9})^{2}}$ units $=\sqrt{(\frac{23}{9})^{2}(\frac{1}{2})^{2}+(\frac{23}{9})^{2}}$ units $=\sqrt{(\frac{23}{9})^{2}(\frac{1}{4}+1)}$ units $=\frac{23}{9} \sqrt{\frac{5}{4}}$ units $=\frac{23}{9} \times \frac{\sqrt{5}}{2}$ units $=\frac{23 \sqrt{5}}{18}$ units Thus, the required distance is 18 units Answer : Let $y=m x+c$ be the line through point $($ - 1,2$)$. Accordingly, $2=m(- 1)+c$. $\Rightarrow 2=- m+c$ $\Rightarrow c=m+2$ $\therefore y=m x+m+2$ The given line is $x+y=4$. On solving equations (1) and (2), we obtain $
\begin{aligned}
& x=\frac{2-m}{m+1} \text{ and } y=\frac{5 m+2}{m+1} \\
& \therefore(\frac{2-m}{m+1}, \frac{5 m+2}{m+1}) \text{ is the point of intersection of lines (1) and (2). }
\end{aligned}
$ Since this point is at a distance of 3 units from point (- 1,2 ), according to distance formula, $
\begin{aligned}
& \sqrt{(\frac{2-m}{m+1}+1)^{2}+(\frac{5 m+2}{m+1}-2)^{2}}=3 \\
\Rightarrow & (\frac{2-m+m+1}{m+1})^{2}+(\frac{5 m+2-2 m-2}{m+1})^{2}=3^{2} \\
\Rightarrow & \frac{9}{(m+1)^{2}}+\frac{9 m^{2}}{(m+1)^{2}}=9 \\
\Rightarrow & \frac{1+m^{2}}{(m+1)^{2}}=1 \\
\Rightarrow & 1+m^{2}=m^{2}+1+2 m \\
\Rightarrow & 2 m=0 \\
\Rightarrow & m=0
\end{aligned}
$ Thus, the slope of the required line must be zero i.e., the line must be parallel to the $x$-axis. Answer : Let $A(1,3)$ and $B(-4,1)$ be the coordinates of the end points of the hypotenuse. Now, plotting the line segment joining the points $A(1,3)$ and $B(-4,1)$ on the coordinate plane, we will get two right triangles with $A B$ as the hypotenuse. Now from the diagram, it is clear that the point of intersection of the other two legs of the right triangle having $A B$ as the hypotenuse can be either $P$ or $Q$. CASE 1: When $\angle $ APB is taken. The perpendicular sides in $\angle $ APB are AP and PB. Now, side $P B$ is parallel to $x$-axis and at a distance of 1 units above $x$-axis. So, equation of $P B$ is, $y=1$ or $y-1=0$. The side AP is parallel to $y$-axis and at a distance of 1 units on the right of $y$-axis. So, equation of $A P$ is $x=1$ or $x-1=0$. CASE 2: When $\angle $ AQB is taken. The perpendicular sides in $\angle $ AQB are AQ and QB. Now, side $A Q$ is parallel to $x$-axis and at a distance of 3 units above $x$-axis. So, equation of $A Q$ is, $y=3$ or $y-3=0$. The side QB is parallel to $y$-axis and at a distance of 4 units on the left of $y$-axis. So, equation of $QB$ is $x=-4$ or $x+4=0$. Hence, the equation of the legs are : $x=1, y=1$ or $x=-4, y=3$ Answer : The equation of the given line is $x+3 y=7$ Let point $B(a, b)$ be the image of point $A(3,8)$. Accordingly, line (1) is the perpendicular bisector of $A B$. Slope of $AB=\frac{b-8}{a-3}$, while the slope of line $(1)=-\frac{1}{3}$ Since line (1) is perpendicular to $A B$, $$
\begin{align*}
& (\frac{b-8}{a-3}) \times(-\frac{1}{3})=-1 \\
& \Rightarrow \frac{b-8}{3 a-9}=1 \\
& \Rightarrow b-8=3 a-9 \\
& \Rightarrow 3 a-b=1 \tag{2}
\end{align*}
$$ Mid-point of $AB=(\frac{a+3}{2}, \frac{b+8}{2})$ The mid-point of line segment $A B$ will also satisfy line (1). Hence, from equation (1), we have $(\frac{a+3}{2})+3(\frac{b+8}{2})=7$ $\Rightarrow a+3+3 b+24=14$ $\Rightarrow a+3 b=-13$ On solving equations (2) and (3), we obtain $a=$ - 1 and $b=$ -4. Thus, the image of the given point with respect to the given line is (-1, -4). Answer : The equations of the given lines are $y=3 x+1 \ldots(1)$ $2 y=x+3$
$y=m x+4 \ldots(3)$ Slope of line (1), $m_1=3$ Slope of line (2), $m_2=\frac{1}{2}$ Slope of line (3), $m_3=m$ It is given that lines (1) and (2) are equally inclined to line (3). This means that the angle between lines (1) and (3) equals the angle between lines (2) and (3). $\therefore|\frac{m_1-m_3}{1+m_1 m_3}|=|\frac{m_2-m_3}{1+m_2 m_3}|$ $\Rightarrow|\frac{3-m}{1+3 m}|=|\frac{\frac{1}{2}-m}{1+\frac{1}{2} m}|$ $\Rightarrow|\frac{3-m}{1+3 m}|=|\frac{1-2 m}{m+2}|$ $\Rightarrow \frac{3-m}{1+3 m}= \pm(\frac{1-2 m}{m+2})$ $\Rightarrow \frac{3-m}{1+3 m}=\frac{1-2 m}{m+2}$ or $\frac{3-m}{1+3 m}=-(\frac{1-2 m}{m+2})$ If $\frac{3-m}{1+3 m}=\frac{1-2 m}{m+2}$, then $(3-m)(m+2)=(1-2 m)(1+3 m)$ $\Rightarrow-m^{2}+m+6=1+m-6 m^{2}$ $\Rightarrow 5 m^{2}+5=0$ $\Rightarrow(m^{2}+1)=0$ $\Rightarrow m=\sqrt{-1}$, which is not real Hence, this case is not posible. If $\frac{3-m}{1+3 m}=-(\frac{1-2 m}{m+2})$, then $\Rightarrow(3-m)(m+2)=-(1-2 m)(1+3 m)$ $\Rightarrow-m^{2}+m+6=-(1+m-6 m^{2})$ $\Rightarrow 7 m^{2}-2 m-7=0$ $\Rightarrow m=\frac{2 \pm \sqrt{4-4(7)(-7)}}{2(7)}$ $\Rightarrow m=\frac{2 \pm 2 \sqrt{1+49}}{14}$ $\Rightarrow m=\frac{1 \pm 5 \sqrt{2}}{7}$ Thus, the required value of $m$ is $\frac{1 \pm 5 \sqrt{2}}{7}$. Answer : The equations of the given lines are $x+y$ - $5=0$ $3 x$ - $2 y+7=0$ The perpendicular distances of $P(x, y)$ from lines (1) and (2) are respectively given by $
d_1=\frac{|x+y-5|}{\sqrt{(1)^{2}+(1)^{2}}} \text{ and } d_2=\frac{|3 x-2 y+7|}{\sqrt{(3)^{2}+(-2)^{2}}}
$ i.e., $d_1=\frac{|x+y-5|}{\sqrt{2}}$ and $d_2=\frac{|3 x-2 y+7|}{\sqrt{13}}$ It is given that $d_1+d_2=10$
$\therefore \frac{|x+y-5|}{\sqrt{2}}+\frac{|3 x-2 y+7|}{\sqrt{13}}=10$ $\Rightarrow \sqrt{13}|x+y-5|+\sqrt{2}|3 x-2 y+7|-10 \sqrt{26}=0$ $\Rightarrow \sqrt{13}(x+y-5)+\sqrt{2}(3 x-2 y+7)-10 \sqrt{26}=0$ [Assuming $(x+y-5)$ and $(3 x-2 y+7)$ are positive] $\Rightarrow \sqrt{13} x+\sqrt{13} y-5 \sqrt{13}+3 \sqrt{2} x-2 \sqrt{2} y+7 \sqrt{2}-10 \sqrt{26}=0$ $\Rightarrow x(\sqrt{13}+3 \sqrt{2})+y(\sqrt{13}-2 \sqrt{2})+(7 \sqrt{2}-5 \sqrt{13}-10 \sqrt{26})=0$ which is the equation of a line. Similarly, we can obtain the equation of line for any signs of $(x+y-5)$ and $(3 x-2 y+7)$. Thus, point $P$ must move on a line. Answer : The equations of the given lines are $9 x+6 y - 7=0$ $3 x+2 y+6=0$… Let $P(h, k)$ be the arbitrary point that is equidistant from lines (1) and (2). The perpendicular distance of $P(h, k)$ from line (1) is given by $
d_1=\frac{|9 h+6 k-7|}{(9)^{2}+(6)^{2}}=\frac{|9 h+6 k-7|}{\sqrt{117}}=\frac{|9 h+6 k-7|}{3 \sqrt{13}}
$ The perpendicular distance of $P(h, k)$ from line (2) is given by $
d_2=\frac{|3 h+2 k+6|}{\sqrt{(3)^{2}+(2)^{2}}}=\frac{|3 h+2 k+6|}{\sqrt{13}}
$ Since $P(h, k)$ is equidistant from lines (1) and (2), $d_1=d_2$ $$
\begin{aligned}
& \therefore \frac{|9 h+6 k-7|}{3 \sqrt{13}}=\frac{|3 h+2 k+6|}{\sqrt{13}} \\
& \Rightarrow 9 h+6 k-7|=3| 3 h+2 k+6 \mid \\
& \Rightarrow 9 h+6 k-7 \mid= \pm 3(3 h+2 k+6) \\
& \Rightarrow 9 h+6 k-7=3(3 h+2 k+6) \text{ or } 9 h+6 k-7=-3(3 h+2 k+6)
\end{aligned}
$$ The case $9 h+6 k-7=3(3 h+2 k+6)$ is not possible as $9 h+6 k-7=3(3 h+2 k+6) \Rightarrow-7=18$ (which is absurd) $\therefore h+6 k-7=-3(3 h+2 k+6)$ $9h + 6k -7 = -9h-6k-18$ $\Rightarrow 18 h+12 k+11=0$ Thus, the required equation of the line is $18 x+12 y+11=0$. Answer : $9h + 6k -7 = -9h-6k-18$ Let the coordinates of point $A$ be $(a, 0)$. Draw a line (AL) perpendicular to the $x$-axis. We know that angle of incidence is equal to angle of reflection. Hence, let $\angle BAL=\angle CAL=\varnothing$ Let $\angle CAX=\theta$ $\therefore \angle OAB=180^{\circ} a \ell(\theta+2 \Phi)=180^{\circ} a \ell[\theta+2(90^{\circ} a \ell \theta)]$ $
\begin{aligned}
& =180^{\circ} a \epsilon \theta a \epsilon 180^{\circ}+2 \theta \\
& =\theta \\
& \therefore \angle B A X=180^{\circ} - \theta
\end{aligned}
$ Now, slope of line $AC=\frac{3-0}{5-a}$ $\Rightarrow \tan \theta=\frac{3}{5-a}$ Slope of line $AB=\frac{2-0}{1-a}$ $\Rightarrow \tan (180^{\circ}-\theta)=\frac{2}{1-a}$ $\Rightarrow-\tan \theta=\frac{2}{1-a}$ $\Rightarrow \tan \theta=\frac{2}{a-1}$ From equations (1) and (2), we obtain $
\begin{aligned}
& \frac{3}{5-a}=\frac{2}{a-1} \\
& \Rightarrow 3 a-3=10-2 a \\
& \Rightarrow a=\frac{13}{5}
\end{aligned}
$ Thus, the coordinates of point $A$ are $(\frac{13}{5}, 0)$. Answer : The equation of the given line is $\frac{x}{a} \cos \theta+\frac{y}{b} \sin \theta=1$ Or, $b x \cos \theta+a y \sin \theta-a b=0$ Length of the perpendicular from point $(\sqrt{a^{2}-b^{2}}, 0)$ to line (1) is $p_1=\frac{|b \cos \theta(\sqrt{a^{2}-b^{2}})+a \sin \theta(0)-a b|}{\sqrt{b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta}}=\frac{|b \cos \theta \sqrt{a^{2}-b^{2}}-a b|}{\sqrt{b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta}}$ Length of the perpendicular from point $(-\sqrt{a^{2}-b^{2}}, 0)$ to line (2) is $p_2=\frac{|b \cos \theta(-\sqrt{a^{2}-b^{2}})+a \sin \theta(0)-a b|}{\sqrt{b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta}}=\frac{|b \cos \theta \sqrt{a^{2}-b^{2}}+a b|}{\sqrt{b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta}}$ On multiplying equations (2) and (3), we obtain $
\begin{aligned}
& p_1 p_2=\frac{|b \cos \theta \sqrt{a^{2}-b^{2}}-a b|(b \cos \theta \sqrt{a^{2}-b^{2}}+a b) \mid}{(\sqrt{b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta})^{2}} \\
& =\frac{|(b \cos \theta \sqrt{a^{2}-b^{2}}-a b)(b \cos \theta \sqrt{a^{2}-b^{2}}+a b)|}{(b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta)} \\
& =\frac{|(b \cos \theta \sqrt{a^{2}-b^{2}})^{2}-(a b)^{2}|}{(b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta)} \\
& =\frac{|b^{2} \cos ^{2} \theta(a^{2}-b^{2})-a^{2} b^{2}|}{(b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta)} \\
& =\frac{|a^{2} b^{2} \cos ^{2} \theta-b^{4} \cos ^{2} \theta-a^{2} b^{2}|}{b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta} \\
& =\frac{b^{2}|a^{2} \cos ^{2} \theta-b^{2} \cos ^{2} \theta-a^{2}|}{b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta} \\
& =\frac{b^{2}|a^{2} \cos ^{2} \theta-b^{2} \cos ^{2} \theta-a^{2} \sin ^{2} \theta-a^{2} \cos ^{2} \theta|}{b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta} \quad[\sin ^{2} \theta+\cos ^{2} \theta=1] \\
& =\frac{b^{2}|-(b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta)|}{b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta} \\
& =\frac{b^{2}(b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta)}{(b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta)} \\
& =b^{2}
\end{aligned}
$ Hence, proved. Answer : The equations of the given lines are $2 x$ - $3 y+4=0$ $3 x+4 y-=0$ $6 x$ - $7 y+8=0$ The person is standing at the junction of the paths represented by lines (1) and (2). On solving equations (1) and (2), we obtain $
x=-\frac{1}{17} \text{ and } y=\frac{22}{17}
$ Thus, the person is standing at point $(-\frac{1}{17}, \frac{22}{17})$. The person can reach path (3) in the least time if he walks along the perpendicular line to (3) from point $(-\frac{1}{17}, \frac{22}{17})$ Slope of the line $(3)=\frac{6}{7}$ $\therefore$ Slope of the line perpendicular to line (3) $
=-\frac{1}{(\frac{6}{7})}=-\frac{7}{6}
$ The equation of the line passing through $(-\frac{1}{17}, \frac{22}{17})$ and having a slope of $-\frac{7}{6}$ is given by $
\begin{aligned}
& (y-\frac{22}{17})=-\frac{7}{6}(x+\frac{1}{17}) \\
& 6(17 y-22)=-7(17 x+1) \\
& 102 y-132=-119 x-7 \\
& 119 x+102 y=125
\end{aligned}
$ Hence, the path that the person should follow is $119 x+102 y=125$. Slope $(m)$ of a non-vertical line passing through the points $(x_1, y_1)$ and $(x_2, y_2)$ is given by $m=\frac{y_2-y_1}{x_2-x_1}=\frac{y_1-y_2}{x_1-x_2}, \quad x_1 \neq x_2$. If a line makes an angle a with the positive direction of $x$-axis, then the slope of the line is given by $m=\tan \alpha, \alpha \neq 90^{\circ}$. Slope of horizontal line is zero and slope of vertical line is undefined. An acute angle (say $\theta$ ) between lines $L_1$ and $L_2$ with slopes $m_1$ and $m_2$ is given by $\tan \theta=|\frac{m_2-m_1}{1+m_1 m_2}|, 1+m_1 m_2 \neq 0$. Two lines are parallel if and only if their slopes are equal. Two lines are perpendicular if and only if product of their slopes is -1 . Three points A, B and C are collinear, if and only if slope of $AB=$ slope of $BC$. Equation of the horizontal line having distance $a$ from the $x$-axis is either $y=a$ or $y=-a$. Equation of the vertical line having distance $b$ from the $y$-axis is either $x=b$ or $x=-b$. The point $(x, y)$ lies on the line with slope $m$ and through the fixed point $(x_o, y_o)$, if and only if its coordinates satisfy the equation $y-y_0=m(x-x_0)$. Equation of the line passing through the points $(x_1, y_1)$ and $(x_2, y_2)$ is given by $y-y_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1)$. The point $(x, y)$ on the line with slope $m$ and $y$-intercept $c$ lies on the line if and only if $y=m x+c$. If a line with slope $m$ makes $x$-intercept $d$. Then equation of the line is $y=m(x-d)$. Equation of a line making intercepts $a$ and $b$ on the $x$-and $y$-axis, respectively, is $\frac{x}{a}+\frac{y}{b}=1$. Any equation of the form $A x+By+C=0$, with $A$ and $B$ are not zero, simultaneously, is called the general linear equation or general equation of a line. The perpendicular distance $(d)$ of a line $A x+B y+C=0$ from a point $(x_1, y_1)$ is given by $d=\frac{|A x_1+B y_1+C|}{\sqrt{A^{2}+B^{2}}}$. Distance between the parallel lines $A x+B y+C_1=0$ and $A x+B y+C_2=0$, is given by $d=\frac{|C_1-C_2|}{\sqrt{A^{2}+B^{2}}}$.Show Answer
Show Answer
Show Answer
Show Answer
Show Answer
Show Answer
Show Answer
Show Answer
Show Answer
Show Answer
Show Answer
Show Answer
Show Answer
Show Answer
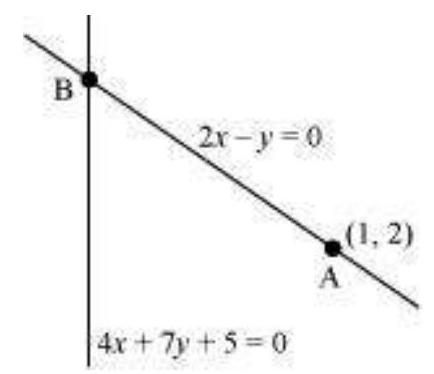
Show Answer
Show Answer
Show Answer
Show Answer
Show Answer
Show Answer
Show Answer
Show Answer
Show Answer
Summary






