In normal life we rarely come across pure substances. Most of these are mixtures containing two or more pure substances. Their utility or importance in life depends on their composition. For example, the properties of brass (mixture of copper and zinc) are quite different from those of German silver (mixture of copper, zinc and nickel) or bronze (mixture of copper and tin); 1 part per million $(\mathrm{ppm})$ of fluoride ions in water prevents tooth decay, while $1.5 \mathrm{ppm}$ causes the tooth to become mottled and high concentrations of fluoride ions can be poisonous (for example, sodium fluoride is used in rat poison); intravenous injections are always dissolved in water containing salts at particular ionic concentrations that match with blood plasma concentrations and so on.

In this Unit, we will consider mostly liquid solutions and their formation. This will be followed by studying the properties of the solutions, like vapour pressure and colligative properties. We will begin with types of solutions and then various alternatives in which concentrations of a solute can be expressed in liquid solution.

2.1 Types of Solutions

Solutions are homogeneous mixtures of two or more than two components. By homogenous mixture we mean that its composition and properties are uniform throughout the mixture. Generally, the component that is present in the largest quantity is known as solvent. Solvent determines the physical state in which solution exists. One or more components present in the solution other than solvent are called solutes. In this Unit we shall consider only binary solutions (i.e., consisting of two components). Here each component may be solid, liquid or in gaseous state and are summarised in Table 2.1.

Type of Solution	Solute	Solvent	Common Examples
Gaseous Solutions	Gas Liquid Solid	Gas Gas Gas	Mixture of oxygen and nitrogen gases Chloroform mixed with nitrogen gas Camphor in nitrogen gas
Liquid Solutions	Gas Liquid Solid	Liquid Liquid Liquid	Oxygen dissolved in water Ethanol dissolved in water Glucose dissolved in water
Solid Solutions	Gas Liquid Solid	Solid Solid Solid	Solution of hydrogen in palladium Amalgam of mercury with sodium Copper dissolved in gold

2.2 Expressing Concentration of Solutions

Composition of a solution can be described by expressing its concentration. The latter can be expressed either qualitatively or quantitatively. For example, qualitatively we can say that the solution is dilute (i.e., relatively very small quantity of solute) or it is concentrated (i.e., relatively very large quantity of solute). But in real life these kinds of description can add to lot of confusion and thus the need for a quantitative description of the solution.

There are several ways by which we can describe the concentration of the solution quantitatively.

(i) Mass percentage $(\mathrm{w} / \mathrm{w})$ : The mass percentage of a component of a solution is defined as:

Mass \% of a component

$$ \begin{equation*} =\frac{\text { Mass of the component in the solution }}{\text { Total mass of the solution }} \times 100 \tag{2.1} \end{equation*} $$

For example, if a solution is described by $10 \%$ glucose in water by mass, it means that $10 \mathrm{~g}$ of glucose is dissolved in $90 \mathrm{~g}$ of water resulting in a $100 \mathrm{~g}$ solution. Concentration described by mass percentage is commonly used in industrial chemical applications. For example, commercial bleaching solution contains 3.62 mass percentage of sodium hypochlorite in water.

(ii) Volume percentage ( $\mathrm{V} / \mathrm{V}$) : The volume percentage is defined as:

Volume $\%$ of a component $=\frac{\text { Volume of the component }}{\text { Total volume of solution }} \times 100$

For example, $10 \%$ ethanol solution in water means that $10 \mathrm{~mL}$ of ethanol is dissolved in water such that the total volume of the solution is $100 \mathrm{~mL}$. Solutions containing liquids are commonly expressed in this unit. For example, a $35 \%(v / v)$ solution of ethylene glycol, an antifreeze, is used in cars for cooling the engine. At this concentration the antifreeze lowers the freezing point of water to $255.4 \mathrm{~K}\left(-17.6^{\circ} \mathrm{C}\right)$.

(iii) Mass by volume percentage (w/V): Another unit which is commonly used in medicine and pharmacy is mass by volume percentage. It is the mass of solute dissolved in $100 \mathrm{~mL}$ of the solution.

(iv) Parts per million: When a solute is present in trace quantities, it is convenient to express concentration in parts per million (ppm) and is defined as:

Parts per million $=$

$$ \begin{equation*} \frac{\text { Number of parts of the component }}{\text { Total number of parts of all components of the solution }} \times 10^{6} \tag{2.3} \end{equation*} $$

As in the case of percentage, concentration in parts per million can also be expressed as mass to mass, volume to volume and mass to volume. A litre of sea water (which weighs $1030 \mathrm{~g}$ ) contains about $6 \times 10^{-3} \mathrm{~g}$ of dissolved oxygen $\left(\mathrm{O_2}\right)$. Such a small concentration is also expressed as $5.8 \mathrm{~g}$ per $10^{6} \mathrm{~g}(5.8 \mathrm{ppm})$ of sea water. The concentration of pollutants in water or atmosphere is often expressed in terms of $\mu \mathrm{g} \mathrm{mL}^{-1}$ or ppm.

(v) Mole fraction: Commonly used symbol for mole fraction is $x$ and subscript used on the right hand side of $x$ denotes the component. It is defined as:

Mole fraction of a component $=$ Number of moles of the component/ Total number of moles of all the components (2.4)

For example, in a binary mixture, if the number of moles of A and B are $n_{\mathrm{A}}$ and $n_{\mathrm{B}}$ respectively, the mole fraction of $\mathrm{A}$ will be

$$ \begin{equation*} x_{\mathrm{A}}=\frac{n_{\mathrm{A}}}{n_{\mathrm{A}}+n_{\mathrm{B}}} \tag{2.5} \end{equation*} $$

For a solution containing i number of components, we have:

$$ \begin{equation*} x_{\mathrm{i}}=\frac{n_{\mathrm{i}}}{n_{1}+n_{2}+\ldots \ldots+n_{\mathrm{i}}}=\frac{n_{\mathrm{i}}}{\sum n_{\mathrm{i}}} \tag{2.6} \end{equation*} $$

It can be shown that in a given solution sum of all the mole fractions is unity, i.e.

$$ \begin{equation*} x_{1}+x_{2}+\ldots \ldots \ldots \ldots \ldots \ldots .+x_{i}=1 \tag{2.7} \end{equation*} $$

Mole fraction unit is very useful in relating some physical properties of solutions, say vapour pressure with the concentration of the solution and quite useful in describing the calculations involving gas mixtures.

Example 2.1

Calculate the mole fraction of ethylene glycol $\left(\mathrm{C_2} \mathrm{H_6} \mathrm{O_2}\right)$ in a solution containing $20 \%$ of $\mathrm{C_2} \mathrm{H_6} \mathrm{O_2}$ by mass.

Solution

Assume that we have $100 \mathrm{~g}$ of solution (one can start with any amount of solution because the results obtained will be the same). Solution will contain $20 \mathrm{~g}$ of ethylene glycol and $80 \mathrm{~g}$ of water.

Molar mass of $\mathrm{C_2} \mathrm{H_6} \mathrm{O_2}=12 \times 2+1 \times 6+16 \times 2=62 \mathrm{~g} \mathrm{~mol}^{-1}$.

Moles of $\mathrm{C_2} \mathrm{H_6} \mathrm{O_2}=\frac{20 \mathrm{~g}}{62 \mathrm{~g} \mathrm{~mol}^{-1}}=0.322 \mathrm{~mol}$

Moles of water $=\frac{80 \mathrm{~g}}{18 \mathrm{~g} \mathrm{~mol}^{-1}}=4.444 \mathrm{~mol}$

$\mathrm{x_\text {glycol }}=\frac{\text { moles of } \mathrm{C_2} \mathrm{H_6} \mathrm{O_2}}{\text { moles of } \mathrm{C_2} \mathrm{H_6} \mathrm{O_2}+\text { moles of } \mathrm{H_2} \mathrm{O}}$

$$ =\frac{0.322 \mathrm{~mol}}{0.322 \mathrm{~mol}+4.444 \mathrm{~mol}}=0.068 $$

Similarly, $x_{\text {water }}=\frac{4.444 \mathrm{~mol}}{0.322 \mathrm{~mol}+4.444 \mathrm{~mol}}=0.932$

Mole fraction of water can also be calculated as: $1-0.068=0.932$

(vi) Molarity: MMolarity $(M)$ is defined as number of moles of solute dissolved in one litre (or one cubic decimetre) of solution,

$$ \begin{equation*} \text { Molarity }=\frac{\text { Moles of solute }}{\text { Volume of solution in litre }} \tag{2.8} \end{equation*} $$

For example, $0.25 \mathrm{~mol} \mathrm{~L}^{-1}$ (or $0.25 \mathrm{M}$ ) solution of $\mathrm{NaOH}$ means that $0.25 \mathrm{~mol}$ of $\mathrm{NaOH}$ has been dissolved in one litre (or one cubic decimetre).

Example 2.2

Calculate the molarity of a solution containing $5 \mathrm{~g}$ of $\mathrm{NaOH}$ in $450 \mathrm{~mL}$ solution.

Solution

$$ \text { Moles of } \mathrm{NaOH}=\frac{5 \mathrm{~g}}{40 \mathrm{~g} \mathrm{~mol}^{-1}}=0.125 \mathrm{~mol} $$

Volume of the solution in litres $=450 \mathrm{~mL} / 1000 \mathrm{~mL} \mathrm{~L}^{-1}$

Using equation (2.8),

$$ \begin{aligned} \text { Molarity } & =\frac{0.125 \mathrm{~mol} \times 1000 \mathrm{~mL} \mathrm{~L}^{-1}}{450 \mathrm{~mL}}=0.278 \mathrm{M} \ & =0.278 \mathrm{~mol} \mathrm{~L}^{-1} \ & =0.278 \mathrm{~mol} \mathrm{dm}^{-3} \end{aligned} $$

(vii) Molality: Molality $(m)$ is defined as the number of moles of the solute per kilogram $(\mathrm{kg})$ of the solvent and is expressed as:

$$ \begin{equation*} \text { Molality }(\mathrm{m})=\frac{\text { Moles of solute }}{\text { Mass of solvent in } \mathrm{kg}} \tag{2.9} \end{equation*} $$

For example, $1.00 \mathrm{~mol} \mathrm{~kg}^{-1}$ (or $1.00 \mathrm{~m}$ ) solution of $\mathrm{KCl}$ means that $1 \mathrm{~mol}(74.5 \mathrm{~g})$ of $\mathrm{KCl}$ is dissolved in $1 \mathrm{~kg}$ of water.

Each method of expressing concentration of the solutions has its own merits and demerits. Mass \%, ppm, mole fraction and molality are independent of temperature, whereas molarity is a function of temperature. This is because volume depends on temperature and the mass does not.

Example 2.3

Calculate molality of $2.5 \mathrm{~g}$ of ethanoic acid $\left(\mathrm{CH_3} \mathrm{COOH}\right)$ in $75 \mathrm{~g}$ of benzene.

Solution

Moles of $\mathrm{C_2} \mathrm{H_4} \mathrm{O_2}=\frac{2.5 \mathrm{~g}}{60 \mathrm{~g} \mathrm{~mol}^{-1}}=0.0417 \mathrm{~mol}$

Mass of benzene in $\mathrm{kg}=75 \mathrm{~g} / 1000 \mathrm{~g} \mathrm{~kg}^{-1}=75 \times 10^{-3} \mathrm{~kg}$

Molality of $\mathrm{C_2} \mathrm{H_4} \mathrm{O_2}=\frac{\text { Moles of } \mathrm{C_2} \mathrm{H_4} \mathrm{O_2}}{\mathrm{~kg} \text { of benzene }}=\frac{0.0417 \mathrm{~mol} \times 1000 \mathrm{~g} \mathrm{~kg}^{-1}}{75 \mathrm{~g}}$

$$ =0.556 \mathrm{~mol} \mathrm{~kg}^{-1} $$

Intext Questions

2.1 Calculate the mass percentage of benzene $\left(\mathrm{C_6} \mathrm{H_6}\right)$ and carbon tetrachloride $\left(\mathrm{CCl_4}\right)$ if $22 \mathrm{~g}$ of benzene is dissolved in $122 \mathrm{~g}$ of carbon tetrachloride.

Answer

Mass percentage of $\mathrm{C_6} \mathrm{H_6}$

$$ =\frac{\text { Mass of } \mathrm{C_6} \mathrm{H_6}}{\text { Total mass of the solution }} \times 100 \% $$

$$ \begin{aligned} & =\frac{\text { Mass of } \mathrm{C_6} \mathrm{H_6}}{\text { Mass of } \mathrm{C_6} \mathrm{H_6}+\text { Mass of } \mathrm{CCl_4}} \times 100 \% \\ & =\frac{22}{22+122} \times 100 \% \\ & =15.28 \% \end{aligned} $$

Mass percentage of $\mathrm{CCl_4} \quad$ Total mass of the solution

$$ =\frac{\text { Mass of } \mathrm{CCl_4}}{\text { Total mass of the solution }} \times 100 \% $$

$$ =\frac{\text { Mass of } \mathrm{CCl_4}}{\text { Mass of } \mathrm{C_6} \mathrm{H_6}+\text { Mass of } \mathrm{CCl_4}} \times 100 \% $$

$=\frac{122}{22+122} \times 100 \%$

$=84.72 \%$

Alternatively,

Mass percentage of $\mathrm{CCl_4}=(100-15.28) \%$

$=84.72 \%$

2.2 Calculate the mole fraction of benzene in solution containing $30 \%$ by mass in carbon tetrachloride.

Answer

Let the total mass of the solution be $100 \mathrm{~g}$ and the mass of benzene be $30 \mathrm{~g}$.

$\therefore$ Mass of carbon tetrachloride $=(100-30) \mathrm{g}$

$=70 \mathrm{~g}$

Molar mass of benzene $\left(\mathrm{C_6} \mathrm{H_6}\right)=(6 \times 12+6 \times 1) \mathrm{g} \mathrm{mol}^{-1}$

$=78 \mathrm{~g} \mathrm{~mol}^{-1}$

$\therefore$ Number of moles of

$$ \mathrm{C_6} \mathrm{H_6}=\frac{30}{78} \mathrm{~mol} $$

$=0.3846 \mathrm{~mol}$

Molar mass of carbon tetrachloride $\left(\mathrm{CCl_4}\right)=1 \times 12+4 \times 355$

$=154 \mathrm{~g} \mathrm{~mol}^{-1}$

$\therefore$ Number of moles of $\mathrm{CCl_4}=\frac{70}{154} \mathrm{~mol}$

$=0.4545 \mathrm{~mol}$

Thus, the mole fraction of $\mathrm{C_6} \mathrm{H_6}$ is given as:

Number of moles of $\mathrm{C_6} \mathrm{H_6}$

Number of moles of $\mathrm{C_6} \mathrm{H_6}+$ Number of moles of $\mathrm{CCl_4}$

$=\frac{0.3846}{0.3846+0.4545}$

$=0.458$

2.3 Calculate the molarity of each of the following solutions: (a) $30 \mathrm{~g}$ of $\mathrm{Co}\left(\mathrm{NO_3}\right)_{2} .6 \mathrm{H_2} \mathrm{O}$ in $4.3 \mathrm{~L}$ of solution (b)30 $\mathrm{mL}$ of $0.5 \mathrm{M} \mathrm{H_2} \mathrm{SO_4}$ diluted to $500 \mathrm{~mL}$.

Answer

Molarity is given by:

$$ \text { Molarity }=\frac{\text { Moles of solute }}{\text { Volume of solution in litre }} $$

(a) Molar mass of $\mathrm{Co}\left(\mathrm{NO_3}\right)_{2} \cdot 6 \mathrm{H_2} \mathrm{O}=59+2(14+3 \times 16)+6 \times 18$

$=291 \mathrm{~g} \mathrm{~mol}^{-1}$

$\therefore$ Moles of $\mathrm{Co}\left(\mathrm{NO_3}\right)_{2} \cdot 6 \mathrm{H_2} \mathrm{O}=\frac{30}{291} \mathrm{~mol}$

$=0.103 \mathrm{~mol}$

Therefore, molarity $=\frac{0.103 \mathrm{~mol}}{4.3 \mathrm{~L}}$

$=0.023 \mathrm{M}$

(b) Number of moles present in $1000 \mathrm{~mL}$ of $0.5 \mathrm{M} \mathrm{H_2} \mathrm{SO_4}=0.5 \mathrm{~mol}$ $\therefore$ Number of moles present in $30 \mathrm{~mL}$ of $0.5 \mathrm{M} \mathrm{H_2} \mathrm{SO_4}=\frac{0.5 \times 30}{1000} \mathrm{~mol}$

$=0.015 \mathrm{~mol}$

Therefore, molarity

$$ =\frac{0.015}{0.5 \mathrm{~L}} \mathrm{~mol} $$

$=0.03 \mathrm{M}$

2.4 Calculate the mass of urea $\left(\mathrm{NH_2} \mathrm{CONH_2}\right)$ required in making $2.5 \mathrm{~kg}$ of 0.25 molal aqueous solution.

Answer

Molar mass of urea $\left(\mathrm{NH_2} \mathrm{CONH_2}\right)=2(1 \times 14+2 \times 1)+1 \times 12+1 \times 16$

$=60 \mathrm{~g} \mathrm{~mol}^{-1}$

0.25 molar aqueous solution of urea means:

$1000 \mathrm{~g}$ of water contains $0.25 \mathrm{~mol}=(0.25 \times 60) \mathrm{g}$ of urea

$=15 \mathrm{~g}$ of urea

That is,

$(1000+15) \mathrm{g}$ of solution contains $15 \mathrm{~g}$ of urea

Therefore, $2.5 \mathrm{~kg}(2500 \mathrm{~g})$ of solution contains

$$ =\frac{15 \times 2500}{1000+15} \mathrm{~g} $$

$=36.95 \mathrm{~g}$

$=37 \mathrm{~g}$ of urea (approximately)

Hence, mass of urea required $=37 \mathrm{~g}$

Note:There is a slight variation in this answer and the one given in the NCERT textbook.

2.5 Calculate (a)molality (b)molarity and (c)mole fraction of $\mathrm{KI}$ if the density of $20 \%$ (mass/mass) aqueous $\mathrm{KI}$ is $1.202 \mathrm{~g} \mathrm{~mL}^{-1}$.

Answer

(a) Molar mass of $\mathrm{KI}=39+127=166 \mathrm{~g} \mathrm{~mol}^{-1}$

$20 \%$ (mass/mass) aqueous solution of $\mathrm{KI}$ means $20 \mathrm{~g}$ of $\mathrm{KI}$ is present in $100 \mathrm{~g}$ of solution.

That is, $20 \mathrm{~g}$ of KI is present in $(100-20) \mathrm{g}$ of water $=80 \mathrm{~g}$ of water

Therefore, molality of the solution

$$ =\frac{\text { Moles of KI }}{\text { Mass of water in } \mathrm{kg}} $$

$=\frac{\frac{20}{166}}{0.08} \mathrm{~m}$

$=1.506 \mathrm{~m}$

$=1.51 \mathrm{~m}$ (approximately)

(b) It is given that the density of the solution $=1.202 \mathrm{~g} \mathrm{~mL}^{-1}$

$=\frac{100 \mathrm{~g}}{1.202 \mathrm{~g} \mathrm{~mL}^{-1}}$

$$ =\frac{\text { Mass }}{\text { Density }} $$

$=83.19 \mathrm{~mL}$

$=83.19 \times 10^{-3} \mathrm{~L}$

Therefore, molarity of the solution

$$ =\frac{\frac{20}{166} \mathrm{~mol}}{83.19 \times 10^{-3} \mathrm{~L}} $$

$=1.45 \mathrm{M}$

(c) Moles of KI

$$ =\frac{20}{166}=0.12 \mathrm{~mol} $$

Moles of water

$$ =\frac{80}{18}=4.44 \mathrm{~mol} $$

Therefore, mole fraction of $\mathrm{KI}$

$$ =\frac{\text { Moles of KI }}{\text { Moles of KI }+ \text { Moles of water }} $$

$$ =\frac{0.12}{0.12+4.44} $$

$=0.0263$

2.3 Solubility

Solubility of a substance is its maximum amount that can be dissolved in a specified amount of solvent at a specified temperature. It depends upon the nature of solute and solvent as well as temperature and pressure. Let us consider the effect of these factors in solution of a solid or a gas in a liquid.

2.3.1 Solubility of a Solid in a Liquid

Every solid does not dissolve in a given liquid. While sodium chloride and sugar dissolve readily in water, naphthalene and anthracene do not. On the other hand, naphthalene and anthracene dissolve readily in benzene but sodium chloride and sugar do not. It is observed that polar solutes dissolve in polar solvents and non polar solutes in nonpolar solvents. In general, a solute dissolves in a solvent if the intermolecular interactions are similar in the two or we may say like dissolves like.

When a solid solute is added to the solvent, some solute dissolves and its concentration increases in solution. This process is known as dissolution. Some solute particles in solution collide with the solid solute particles and get separated out of solution. This process is known as crystallisation. A stage is reached when the two processes occur at the same rate. Under such conditions, number of solute particles going into solution will be equal to the solute particles separating out and a state of dynamic equilibrium is reached.

$$ \begin{equation*} \text { Solute }+ \text { Solvent } \rightleftharpoons \text { Solution } \tag{2.10} \end{equation*} $$

At this stage the concentration of solute in solution will remain constant under the given conditions, i.e., temperature and pressure. Similar process is followed when gases are dissolved in liquid solvents. Such a solution in which no more solute can be dissolved at the same temperature and pressure is called a saturated solution. An unsaturated solution is one in which more solute can be dissolved at the same temperature. The solution which is in dynamic equilibrium with undissolved solute is the saturated solution and contains the maximum amount of solute dissolved in a given amount of solvent. Thus, the concentration of solute in such a solution is its solubility.

Earlier we have observed that solubility of one substance into another depends on the nature of the substances. In addition to these variables, two other parameters, i.e., temperature and pressure also control this phenomenon.

Effect of temperature

The solubility of a solid in a liquid is significantly affected by temperature changes. Consider the equilibrium represented by equation 1.10 . This, being dynamic equilibrium, must follow Le Chateliers Principle. In general, if in a nearly saturated solution, the dissolution process is endothermic $(\left.\Delta_{\text {sol }} \mathrm{H}>0\right)$, the solubility should increase with rise in temperature and if it is exothermic $\left(\Delta_{\text {sol }} \mathrm{H}<0\right)$ the solubility should decrease. These trends are also observed experimentally.

Effect of pressure

Pressure does not have any significant effect on solubility of solids in liquids. It is so because solids and liquids are highly incompressible and practically remain unaffected by changes in pressure.

2.3.2 Solubility of a Gas in a Liquid

Many gases dissolve in water. Oxygen dissolves only to a small extent in water. It is this dissolved oxygen which sustains all aquatic life. On the other hand, hydrogen chloride gas (HCl) is highly soluble in water. Solubility of gases in liquids is greatly affected by pressure and temperature. The solubility of gases increase with increase of pressure. For solution of gases in a solvent, consider a system as shown in Fig. 2.1 (a). The lower part is solution and the upper part is gaseous system at pressure p and temperature T. Assume this system to be in a state of dynamic equilibrium, i.e., under these conditions rate of gaseous particles entering and leaving the solution phase is the same. Now increase the pressure over the solution phase by compressing the gas to a smaller volume [Fig. 2.1 (b)]. This will increase the number of gaseous particles per unit volume over the solution and also the rate at which the gaseous particles are striking the surface of solution to enter it. The solubility of the gas will increase until a new equilibrium is reached resulting in an increase in the pressure of a gas above the solution and thus its solubility increases.

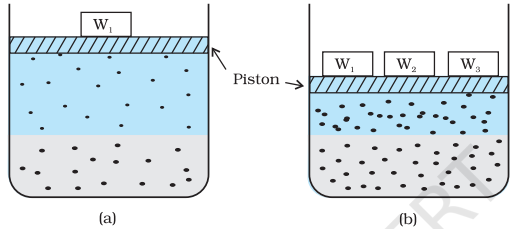
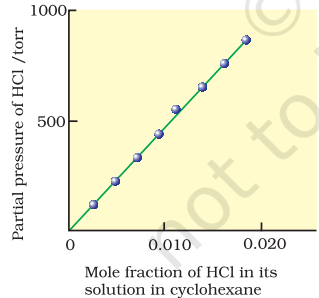
Henry was the first to give a quantitative relation between pressure and solubility of a gas in a solvent which is known as Henry’s law. The law states that at a constant temperature, the solubility of a gas in a liquid is directly proportional to the partial pressure of the gas present above the surface of liquid or solution. Dalton, a contemporary of Henry, also concluded independently that the solubility of a gas in a liquid solution is a function of partial pressure of the gas. If we use the mole fraction of a gas in the solution as a measure of its solubility, then it can be said that the mole fraction of gas in the solution is proportional to the partial pressure of the gas over the solution. The most commonly used form of Henry’s law states that “the partial pressure of the gas in vapour phase (p) is proportional to the mole fraction of the gas $(\boldsymbol{x})$ in the solution" and is expressed as:

$$ \begin{equation*} p=K_{\mathrm{H}} x \tag{2.11} \end{equation*} $$

Here $K_H$ is the Henry’s law constant. If we draw a graph between partial pressure of the gas versus mole fraction of the gas in solution, then we should get a plot of the type as shown in Fig. 2.2.

Different gases have different KH values at the same temperature (Table 2.2). This suggests that KH is a function of the nature of the gas.

It is obvious from equation (2.11) that higher the value of $K_{\mathrm{H}}$ at a given pressure, the lower is the solubility of the gas in the liquid. It can be seen from Table 1.2 that $\mathrm{K_\mathrm{H}}$ values for both $\mathrm{N_2}$ and $\mathrm{O_2}$ increase with increase of temperature indicating that the solubility of gases increases with decrease of temperature. It is due to this reason that aquatic species are more comfortable in cold waters rather than in warm waters.

increases with decrease of temperature. It is due to this reason that aquatic species are more comfortable in cold waters rather than in warm waters.

Henry’s law finds several applications in industry and explains some biological phenomena. Notable among these are:

• To increase the solubility of CO2 in soft drinks and soda water, the bottle is sealed under high pressure.

• Scuba divers must cope with high concentrations of dissolved gases while breathing air at high pressure underwater. Increased pressure increases the solubility of atmospheric gases in blood. When the divers come towards surface, the pressure gradually decreases. This releases the dissolved gases and leads to the formation of bubbles of nitrogen in the blood. This blocks capillaries and creates a medical condition known as bends, which are painful and dangerous to life.

To avoid bends, as well as, the toxic effects of high concentrations of nitrogen in the blood, the tanks used by scuba divers are filled with air diluted with helium (11.7% helium, 56.2% nitrogen and 32.1% oxygen).

• At high altitudes the partial pressure of oxygen is less than that at the ground level. This leads to low concentrations of oxygen in the blood and tissues of people living at high altitudes or climbers. Low blood oxygen causes climbers to become weak and unable to think clearly, symptoms of a condition known as anoxia.

Example 1.4

If $\mathrm{N_2}$ gas is bubbled through water at $293 \mathrm{~K}$, how many millimoles of $\mathrm{N_2}$ gas would dissolve in 1 litre of water? Assume that $\mathrm{N_2}$ exerts a partial pressure of 0.987 bar. Given that Henry’s law constant for $\mathrm{N_2}$ at $293 \mathrm{~K}$ is $76.48 \mathrm{kbar}$.

Solution

The solubility of gas is related to the mole fraction in aqueous solution. The mole fraction of the gas in the solution is calculated by applying Henry’s law. Thus:

$x$ (Nitrogen) $=\frac{p \text { (nitrogen) }}{K_{\mathrm{H}}}=\frac{0.987 \mathrm{bar}}{76,480 \mathrm{bar}}=1.29 \times 10^{-5}$

As 1 litre of water contains $55.5 \mathrm{~mol}$ of it, therefore if $n$ represents number of moles of $\mathrm{N_2}$ in solution,

$x($ Nitrogen $)=\frac{n \mathrm{~mol}}{n \mathrm{~mol}+55.5 \mathrm{~mol}}=\frac{n}{55.5}=1.29 \times 10^{-5}$

( $n$ in denominator is neglected as it is $«55.5$ )

Thus $n=1.29 \times 10^{-5} \times 55.5 \mathrm{~mol}=7.16 \times 10^{-4} \mathrm{~mol}$

$=\frac{7.16 \times 10^{-4} \mathrm{~mol} \times 1000 \mathrm{mmol}}{1 \mathrm{~mol}}=0.716 \mathrm{mmol}$

Effect of Temperature

Solubility of gases in liquids decreases with rise in temperature. When dissolved, the gas molecules are present in liquid phase and the process of dissolution can be considered similar to condensation and heat is evolved in this process. We have learnt in the last Section that dissolution process involves dynamic equilibrium and thus must follow Le Chatelier’s Principle. As dissolution is an exothermic process, the solubility should decrease with increase of temperature.

Intext Questions

2.6 $\mathrm{H_2} \mathrm{~S}$, a toxic gas with rotten egg like smell, is used for the qualitative analysis. If the solubility of $\mathrm{H_2} \mathrm{~S}$ in water at STP is $0.195 \mathrm{~m}$, calculate Henry’s law constant.

Answer

It is given that the solubility of $\mathrm{H_2} \mathrm{~S}$ in water at STP is $0.195 \mathrm{~m}$, i.e., 0.195 mol of $\mathrm{H_2} \mathrm{~S}$ is dissolved in $1000 \mathrm{~g}$ of water.

Moles of water $=\frac{1000 \mathrm{~g}}{18 \mathrm{~g} \mathrm{~mol}^{-1}}$

$=55.56 \mathrm{~mol}$

$$ =\frac{0.195}{0.195+55.56} $$

$$ =\frac{\text { Moles of } \mathrm{H_2} \mathrm{~S}}{\text { Moles of } \mathrm{H_2} \mathrm{~S}+\text { Moles of water }} $$

$=0.0035$

At STP, pressure $(p)=0.987$ bar

According to Henry’s law:

$p=\mathrm{K_\mathrm{H}} X$

$\Rightarrow \mathrm{K_\mathrm{H}}=\frac{p}{x}$

$$ =\frac{0.987}{0.0035} \text { bar } $$

$=282$ bar

2.7 Henry’s law constant for $\mathrm{CO_2}$ in water is $1.67 \times 10^{8} \mathrm{~Pa}$ at $298 \mathrm{~K}$. Calculate the quantity of $\mathrm{CO_2}$ in $500 \mathrm{~mL}$ of soda water when packed under $2.5 \mathrm{~atm}$ $\mathrm{CO_2}$ pressure at $298 \mathrm{~K}$.

Answer

It is given that:

$\mathrm{K_\mathrm{H}}=1.67 \times 10^{8} \mathrm{~Pa}$

$$ p_{\mathrm{CO_2}}=2.5 \mathrm{~atm}=2.5 \times 1.01325 \times 10^{5} \mathrm{~Pa} $$

$=2.533125 \times 10^{5} \mathrm{~Pa}$

According to Henry’s law:

$$ \begin{aligned} p_{\mathrm{CO_2}} & =\mathrm{K_\mathrm{H}} x \\ \Rightarrow x & =\frac{p_{\mathrm{CO_2}}}{\mathrm{~K_\mathrm{H}}} \\ & =\frac{2.533125 \times 10^{5}}{1.67 \times 10^{8}} \end{aligned} $$

$=0.00152$

We can write,

$$ x=\frac{n_{\mathrm{CO_2}}}{n_{\mathrm{CO_2}}+n_{\mathrm{H_2} \mathrm{O}}} \approx \frac{n_{\mathrm{CO_2}}}{n_{\mathrm{H_2} \mathrm{O}}} $$

[Since, $n_{\mathrm{CO_2}}$ is negligible as compared to ${ }^{n_{\mathrm{H_2} \mathrm{O}}}$ ]

In $500 \mathrm{~mL}$ of soda water, the volume of water $=500 \mathrm{~mL}$

[Neglecting the amount of soda present]

We can write:

$500 \mathrm{~mL}$ of water $=500 \mathrm{~g}$ of water

$=\frac{500}{18} \mathrm{~mol}$ of water

$=27.78 \mathrm{~mol}$ of water

Now, $\frac{n_{\mathrm{CO_2}}}{n_{\mathrm{H_2} \mathrm{O}}}=x$

$\frac{n_{\mathrm{CO_2}}}{27.78}=0.00152$

$n_{\mathrm{CO_2}}=0.042 \mathrm{~mol}$

Hence, quantity of $\mathrm{CO_2}$ in $500 \mathrm{~mL}$ of soda water $=(0.042 \times 44) \mathrm{g}$

$=1.848 \mathrm{~g}$

2.4 Vapour Pressure of Liquid Solutions

Liquid solutions are formed when solvent is a liquid. The solute can be a gas, a liquid or a solid. Solutions of gases in liquids have already been discussed in Section 2.3.2. In this Section, we shall discuss the solutions of liquids and solids in a liquid. Such solutions may contain one or more volatile components. Generally, the liquid solvent is volatile. The solute may or may not be volatile. We shall discuss the properties of only binary solutions, that is, the solutions containing two components, namely, the solutions of (i) liquids in liquids and (ii) solids in liquids.

2.4.1 Vapour Pressure of Liquid- Liquid Solutions

Let us consider a binary solution of two volatile liquids and denote the two components as 1 and 2. When taken in a closed vessel, both the components would evaporate and eventually an equilibrium would be established between vapour phase and the liquid phase. Let the total vapour pressure at this stage be ptotal and p1 and p2 be the partial vapour pressures of the two components 1 and 2 respectively. These partial pressures are related to the mole fractions x1 and x2 of the two components 1 and 2 respectively.

The French chemist, Francois Marte Raoult (1886) gave the quantitative relationship between them. The relationship is known as the Raoult’s law which states that for a solution of volatile liquids, the partial vapour pressure of each component of the solution is directly proportional to its mole fraction present in solution.

Thus, for component 1

$$ \begin{aligned} & p_{1} \propto x_{1} \\ & \text { and } \quad p_{1}=p_{1}^{0} x_{1} \end{aligned} $$

where $p_{1}^{0}$ is the vapour pressure of pure component 1 at the same temperature.

Similarly, for component 2

$$ \begin{equation*} p_{2}=p_{2}{ }^{0} x_{2} \tag{2.13} \end{equation*} $$

where $p_{2}{ }^{0}$ represents the vapour pressure of the pure component 2 .

According to Dalton’s law of partial pressures, the total pressure

$(\left.p_{\text {total }}\right)$ over the solution phase in the container will be the sum of the partial pressures of the components of the solution and is given as:

$$ \begin{equation*} p_{\text {total }}=p_{1}+p_{2} \tag{2.14} \end{equation*} $$

Substituting the values of $p_{1}$ and $p_{2}$, we get

$$ \begin{align*} p_{\text {total }} & =x_{1} p_{1}{ }^{0}+x_{2} p_{2}{ }^{0} \\ & =\left(1-x_{2}\right) p_{1}{ }^{0}+x_{2} p_{2}{ }^{0} \tag{2.15}\\ & =p_{1}{ }^{0}+\left(p_{2}{ }^{0}-p_{1}{ }^{0}\right) x_{2} \tag{2.16} \end{align*} $$

Following conclusions can be drawn from equation (2.16). (i) Total vapour pressure over the solution can be related to the mole fraction of any one component. (ii) Total vapour pressure over the solution varies linearly with the mole fraction of component 2.

(iii) Depending on the vapour pressures of the pure components 1 and 2, total vapour pressure over the solution decreases or increases with the increase of the mole fraction of component 1.

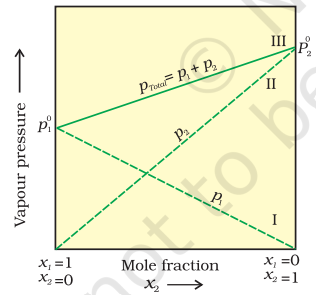
A plot of $p_{1}$ or $p_{2}$ versus the mole fractions $x_{1}$ and $x_{2}$ for a solution gives a linear plot as shown in Fig. 2.3. These lines (I and II) pass through the points for which $x_{1}$ and $x_{2}$ are equal to unity. Similarly the plot (line III) of $p_{\text {total }}$ versus $x_{2}$ is also linear (Fig. 2.3). The minimum value of $p_{\text {total }}$ is $p_{1}{ }^{0}$ and the maximum value is $p_{2}{ }^{0}$, assuming that component 1 is less volatile than component 2 , i.e., $p_{1}{ }^{0}<p_{2}{ }^{0}$.

The composition of vapour phase in equilibrium with the solution is determined by the partial pressures of the components. If $y_{1}$ and $y_{2}$ are the mole fractions of the components 1 and 2 respectively in the vapour phase then, using Dalton’s law of partial pressures:

$$ \begin{align*} & p_{1}=y_{1} p_{\text {total }} \tag{2.17}\\ & p_{2}=y_{2} p_{\text {total }} \tag{2.18} \end{align*} $$

In general

$$ \begin{equation*} p_{\mathrm{i}}=y_{\mathrm{i}} \quad p_{\text {total }} \tag{2.19} \end{equation*} $$

Vapour pressure of chloroform $\left(\mathrm{CHCl_3}\right)$ and dichloromethane $\left(\mathrm{CH_2} \mathrm{Cl_2}\right)$ at $298 \mathrm{~K}$ are $200 \mathrm{~mm} \mathrm{Hg}$ and $415 \mathrm{~mm} \mathrm{Hg}$ respectively. (i) Calculate the vapour pressure of the solution prepared by mixing $25.5 \mathrm{~g}$ of $\mathrm{CHCl_3}$ and $40 \mathrm{~g}$ of $\mathrm{CH_2} \mathrm{Cl_2}$ at $298 \mathrm{~K}$ and, (ii) mole fractions of each component in vapour phase.

(i) Molar mass of $\mathrm{CH_2} \mathrm{Cl_2}=12 \times 1+1 \times 2+35.5 \times 2=85 \mathrm{~g} \mathrm{~mol}^{-1}$

Molar mass of $\mathrm{CHCl_3}=12 \times 1+1 \times 1+35.5 \times 3=119.5 \mathrm{~g} \mathrm{~mol}^{-1}$

Moles of $\mathrm{CH_2} \mathrm{Cl_2} \quad=\frac{40 \mathrm{~g}}{85 \mathrm{~g} \mathrm{~mol}^{-1}}=0.47 \mathrm{~mol}$

Moles of $\mathrm{CHCl_3} \quad=\frac{25.5 \mathrm{~g}}{119.5 \mathrm{~g} \mathrm{~mol}^{-1}}=0.213 \mathrm{~mol}$

Total number of moles $=0.47+0.213=0.683 \mathrm{~mol}$

$$ \begin{aligned} & x_{\mathrm{CH_2} \mathrm{Cl_2}}=\frac{0.47 \mathrm{~mol}}{0.683 \mathrm{~mol}}=0.688 \\ & x_{\mathrm{CHCl_3}}=1.00-0.688=0.312 \end{aligned} $$

Using equation (2.16),

$$ \begin{aligned} p_{\text {total }} & =p_{1}^{0}+\left(p_{2}{ }^{0}-p_{1}{ }^{0}\right) x_{2}=200+(415-200) \times 0.688 \\ & =200+147.9=347.9 \mathrm{~mm} \mathrm{Hg} \end{aligned} $$

(ii) Using the relation (2.19), $y_{\mathrm{i}}=p_{\mathrm{i}} / p_{\text {total }}$, we can calculate the mole fraction of the components in gas phase $\left(y_{\mathrm{i}}\right)$.

$$ \begin{aligned} & p_{\mathrm{CH_2} \mathrm{Cl_2}}=0.688 \times 415 \mathrm{~mm} \mathrm{Hg}=285.5 \mathrm{~mm} \mathrm{Hg} \\ & p_{\mathrm{CHCl_3}}=0.312 \times 200 \mathrm{~mm} \mathrm{Hg}=62.4 \mathrm{~mm} \mathrm{Hg} \\ & y_{\mathrm{CH_2} \mathrm{Cl_2}}=285.5 \mathrm{~mm} \mathrm{Hg} / 347.9 \mathrm{~mm} \mathrm{Hg}=0.82 \\ & y_{\mathrm{CHCl_3}}=62.4 \mathrm{~mm} \mathrm{Hg} / 347.9 \mathrm{~mm} \mathrm{Hg}=0.18 \end{aligned} $$

Note: Since, $\mathrm{CH_2} \mathrm{Cl_2}$ is a more volatile component than $\mathrm{CHCl_3}$, $\left[p_{\mathrm{CH_2} \mathrm{Cl_2}}^{0}=\right.$ $415 \mathrm{~mm} \mathrm{Hg}$ and $p_{\mathrm{CHCl_3}}^{0}=200 \mathrm{~mm} \mathrm{Hg}]$ and the vapour phase is also richer in $\mathrm{CH_2} \mathrm{Cl_2}\left[y_{\mathrm{CH_2} \mathrm{Cl_2}}=0.82\right.$ and $\left.y_{\mathrm{CHCl_3}}=0.18\right]$, it may thus be concluded that at equilibrium, vapour phase will be always rich in the component which is more volatile.

2.4.2 Raoult’s Law as a special case of Henry’s Law

According to Raoult’s law, the vapour pressure of a volatile component in a given solution is given by $p_{\mathrm{i}}=x_{\mathrm{i}} p_{\mathrm{i}}{ }^{0}$. In the solution of a gas in a liquid, one of the components is so volatile that it exists as a gas and we have already seen that its solubility is given by Henry’s law which states that

$$ p=K_{\mathrm{H}} x $$

If we compare the equations for Raoult’s law and Henry’s law, it can be seen that the partial pressure of the volatile component or gas is directly proportional to its mole fraction in solution. Only the proportionality constant $K_{\mathrm{H}}$ differs from $p_{1}{ }^{0}$. Thus, Raoult’s law becomes a special case of Henry’s law in which $K_{\mathrm{H}}$ becomes equal to $p_{1}{ }^{0}$

2.4.3 Vapour Pressure of Solutions of Solids in Liquids

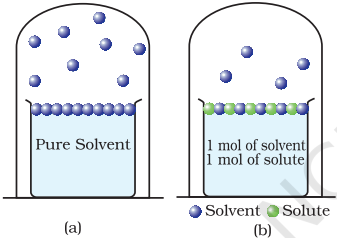
Another important class of solutions consists of solids dissolved in liquid, for example, sodium chloride, glucose, urea and cane sugar in water and iodine and sulphur dissolved in carbon disulphide. Some physical properties of these solutions are quite different from those of pure solvents. For example, vapour pressure. We have learnt in Unit 5, Class XI, that liquids at a given temperature vapourise and under equilibrium conditions the pressure exerted by the vapours of the liquid over the liquid phase is called vapour pressure [Fig. 2.4 (a)]. In a pure liquid the entire surface is occupied by the molecules of the liquid. If a non-volatile solute is added to a solvent to give a solution [Fig. 2.4.(b)], the vapour pressure of the solution is solely from the solvent alone. This vapour pressure of the solution at a given temperature is found to be lower than the vapour pressure of the pure solvent at the same temperature. In the solution, the surface has both solute and solvent molecules; thereby the fraction of the surface covered by the solvent molecules gets reduced. Consequently, the number of solvent molecules escaping from the surface is correspondingly reduced, thus, the vapour pressure is also reduced.

The decrease in the vapour pressure of solvent depends on the quantity of non-volatile solute present in the solution, irrespective of its nature. For example, decrease in the vapour pressure of water by adding $1.0 \mathrm{~mol}$ of sucrose to one $\mathrm{kg}$ of water is nearly similar to that produced by adding $1.0 \mathrm{~mol}$ of urea to the same quantity of water at the same temperature.

Raoult’s law in its general form can be stated as, for any solution the partial vapour pressure of each volatile component in the solution is directly proportional to its mole fraction.

In a binary solution, let us denote the solvent by 1 and solute by 2. When the solute is non-volatile, only the solvent molecules are present in vapour phase and contribute to vapour pressure. Let p1 be the vapour pressure of the solvent, $x_{1}$ be its mole fraction, $p_{i}^{0}$ be its vapour pressure in the pure state. Then according to Raoult’s law

$$ \begin{align*} & p_{1} \propto x_{1} \ & \text { and } \quad p_{1}=x_{1} p_{1}^{0} \tag{2.20} \end{align*} $$

The proportionality constant is equal to the vapour pressure of pure solvent, $p_{1}^{0}$. A plot between the vapour pressure and the mole fraction of the solvent is linear (Fig. 2.5).

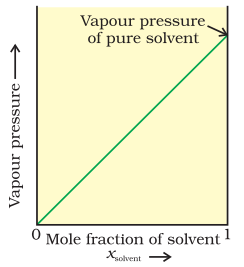
2.5 Ideal and Nonideal Solutions

Liquid-liquid solutions can be classified into ideal and non-ideal solutions on the basis of Raoult’s law.

2.5.1 Ideal Solutions

The solutions which obey Raoult’s law over the entire range of concentration are known as ideal solutions. The ideal solutions have two other important properties. The enthalpy of mixing of the pure components to form the solution is zero and the volume of mixing is also zero, i.e., $$ \begin{equation*} \Delta_{\text {mix }} H=0, \quad \Delta_{\text {mix }} V=0 \tag{2.21} \end{equation*} $$

It means that no heat is absorbed or evolved when the components are mixed. Also, the volume of solution would be equal to the sum of volumes of the two components. At molecular level, ideal behaviour of the solutions can be explained by considering two components A and B. In pure components, the intermolecular attractive interactions will be of types A-A and B-B, whereas in the binary solutions in addition to these two interactions, A-B type of interactions will also be present. If the intermolecular attractive forces between the A-A and B-B are nearly equal to those between A-B, this leads to the formation of ideal solution. A perfectly ideal solution is rare but some solutions are nearly ideal in behaviour. Solution of n-hexane and n-heptane, bromoethane and chloroethane, benzene and toluene, etc. fall into this category.

2.5.2 Non-ideal Solutions

When a solution does not obey Raoult’s law over the entire range of concentration, then it is called non-ideal solution. The vapour pressure of such a solution is either higher or lower than that predicted by Raoult’s law (equation 2.16). If it is higher, the solution exhibits positive deviation and if it is lower, it exhibits negative deviation from Raoult’s law. The plots of vapour pressure as a function of mole fractions for such solutions are shown in Fig. 2.6.

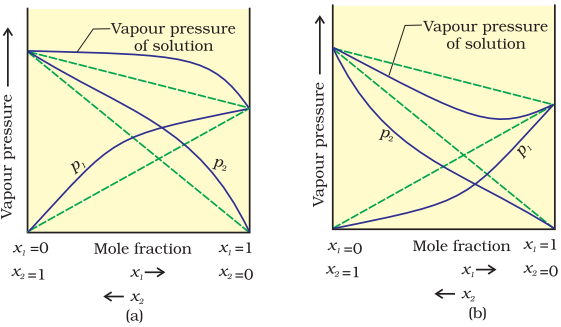
The cause for these deviations lie in the nature of interactions at the molecular level. In case of positive deviation from Raoult’s law, A-B interactions are weaker than those between A-A or B-B, i.e., in this case the intermolecular attractive forces between the solute-solvent molecules are weaker than those between the solute-solute and solvent-solvent molecules. This means that in such solutions, molecules of A (or B) will find it easier to escape than in pure state. This will increase the vapour pressure and result in positive deviation. Mixtures of ethanol and acetone behave in this manner. In pure ethanol, molecules are hydrogen bonded. On adding acetone, its molecules get in between the host molecules and break some of the hydrogen bonds between them. Due to weakening of interactions, the solution shows positive deviation from Raoult’s law [Fig. 2.6 (a)]. In a solution formed by adding carbon disulphide to acetone, the dipolar interactions between solute-solvent molecules are weaker than the respective interactions among the solute-solute and solvent-solvent molecules. This solution also shows positive deviation.

In case of negative deviations from Raoult’s law, the intermolecular attractive forces between A-A and B-B are weaker than those between A-B and leads to decrease in vapour pressure resulting in negative deviations. An example of this type is a mixture of phenol and aniline. In this case the intermolecular hydrogen bonding between phenolic proton and lone pair on nitrogen atom of aniline is stronger than the respective intermolecular hydrogen bonding between similar molecules. Similarly, a mixture of chloroform and acetone forms a solution with negative deviation from Raoult’s law. This is because chloroform molecule is able to form hydrogen bond with acetone molecule as shown.

This decreases the escaping tendency of molecules for each component and consequently the vapour pressure decreases resulting in negative deviation from Raoult’s law [Fig. 2.6. (b)].

Some liquids on mixing, form azeotropes which are binary mixtures having the same composition in liquid and vapour phase and boil at a constant temperature. In such cases, it is not possible to separate the components by fractional distillation. There are two types of azeotropes called minimum boiling azeotrope and maximum boiling azeotrope. The solutions which show a large positive deviation from Raoult’s law form minimum boiling azeotrope at a specific composition.

For example, ethanol-water mixture (obtained by fermentation of sugars) on fractional distillation gives a solution containing approximately 95% by volume of ethanol. Once this composition, known as azeotrope composition, has been achieved, the liquid and vapour have the same composition, and no further separation occurs.

The solutions that show large negative deviation from Raoult’s law form maximum boiling azeotrope at a specific composition. Nitric acid and water is an example of this class of azeotrope. This azeotrope has the approximate composition, 68% nitric acid and 32% water by mass, with a boiling point of 393.5 K.

Intext Question

2.8 The vapour pressure of pure liquids A and B are 450 and $700 \mathrm{~mm} \mathrm{Hg}$ respectively, at $350 \mathrm{~K}$. Find out the composition of the liquid mixture if total vapour pressure is $600 \mathrm{~mm} \mathrm{Hg}$. Also find the composition of the vapour phase.

Answer

It is given that:

$p_{\mathrm{A}}^{0}=450 \mathrm{~mm}$ of $\mathrm{Hg}$

$p_{\mathrm{B}}^{0}=700 \mathrm{~mm}$ of $\mathrm{Hg}$

$p_{\text {total }}=600 \mathrm{~mm}$ of $\mathrm{Hg}$

From Raoult’s law, we have:

$p_{\mathrm{A}}=p_{\mathrm{A}}^{0} x_{\mathrm{A}}$

$p_{\mathrm{B}}=p_{\mathrm{B}}^{0} x_{\mathrm{B}}=p_{\mathrm{B}}^{0}\left(1-x_{\mathrm{A}}\right)$ Therefore, total pressure, $p_{\text {total }}=p_{\mathrm{A}}+p_{\mathrm{B}}$

$\Rightarrow p_{\text {total }}=p_{\mathrm{A}}^{0} x_{\mathrm{A}}+p_{\mathrm{B}}^{0}\left(1-x_{\mathrm{A}}\right)$

$\Rightarrow p_{\text {total }}=p_{\mathrm{A}}^{0} x_{\mathrm{A}}+p_{\mathrm{B}}^{0}-p_{\mathrm{B}}^{0} x_{\mathrm{A}}$

$\Rightarrow p_{\text {total }}=\left(p_{\mathrm{A}}^{0}-p_{\mathrm{B}}^{0}\right) x_{\mathrm{A}}+p_{\mathrm{B}}^{0}$

$\Rightarrow 600=(450-700) x_{\mathrm{A}}+700$

$\Rightarrow-100=-250 x_{\mathrm{A}}$

$\Rightarrow x_{\mathrm{A}}=0.4$

Therefore, $x_{\mathrm{B}}=1-x_{\mathrm{A}}$

$=1-0.4$

$=0.6$

Now, $p_{\mathrm{A}}=p_{\mathrm{A}}^{0} x_{\mathrm{A}}$

$=450 \times 0.4$

$=180 \mathrm{~mm}$ of $\mathrm{Hg}$

$p_{\mathrm{B}}=p_{\mathrm{B}}^{0} x_{\mathrm{B}}$

$=700 \times 0.6$

$=420 \mathrm{~mm}$ of $\mathrm{Hg}$

Now, in the vapour phase:

Mole fraction of liquid $\mathrm{A}=\frac{p_{\mathrm{A}}}{p_{\mathrm{A}}+p_{\mathrm{B}}}$

$$ \begin{aligned} & =\frac{180}{180+420} \\ & =\frac{180}{600} \\ & =0.30 \end{aligned} $$

And, mole fraction of liquid $B=1-0.30$ $=0.70$

2.6 Colligative Properties and Determination of Molar Mass

We have learnt in Section 2.4.3 that the vapour pressure of solution decreases when a non-volatile solute is added to a volatile solvent. There are many properties of solutions which are connected with this decrease of vapour pressure. These are: (1) relative lowering of vapour pressure of the solvent (2) depression of freezing point of the solvent (3) elevation of boiling point of the solvent and (4) osmotic pressure of the solution. All these properties depend on the number of solute particles irrespective of their nature relative to the total number of particles present in the solution. Such properties are called colligative properties (colligative: from Latin: co means together, ligare means to bind). In the following Sections we will discuss these properties one by one.

2.6.1 Relative Lowering of Vapour Pressure

We have learnt in Section 2.4.3 that the vapour pressure of a solvent in solution is less than that of the pure solvent. Raoult established that the lowering of vapour pressure depends only on the concentration of the solute particles and it is independent of their identity. The equation (2.20) given in Section 2.4.3 establishes a relation between vapour pressure of the solution, mole fraction and vapour pressure of the solvent, i.e.,

$$ \begin{equation*} p_{1}=x_{1} p_{1}^{0} \tag{2.22} \end{equation*} $$

The reduction in the vapour pressure of solvent $\left(\Delta p_{1}\right)$ is given as:

$$ \begin{align*} \Delta p_{1} & =p_{1}^{0}-p_{1}=p_{1}^{0}-p_{1}^{0} x_{1} \\ & =p_{1}^{0}\left(1-x_{1}\right) \tag{2.23} \end{align*} $$

Knowing that $x_{2}=1-x_{1}$, equation (1.23) reduces to

$$ \begin{equation*} \Delta p_{1}=x_{2} p_{1}{ }^{0} \tag{2.24} \end{equation*} $$

In a solution containing several non-volatile solutes, the lowering of the vapour pressure depends on the sum of the mole fraction of different solutes. Equation (2.24)

$$ \begin{equation*} \frac{\Delta p_{1}}{p_{1}^{0}}=\frac{p_{1}^{0}-p_{1}}{p_{1}^{0}}=x_{2} \tag{2.25} \end{equation*} $$

The expression on the left hand side of the equation as mentioned earlier is called relative lowering of vapour pressure and is equal to the mole fraction of the solute. The above equation can be written as:

$$ \begin{equation*} \frac{p_{1}^{0}-p_{1}}{p_{1}^{0}}=\frac{n_{2}}{n_{1}+n_{2}}\left(\text { since } x_{2}=\frac{n_{2}}{n_{1}+n_{2}}\right) \tag{2.26} \end{equation*} $$

Here $n_{1}$ and $n_{2}$ are the number of moles of solvent and solute respectively present in the solution. For dilute solutions $n_{2}<n_{1}$, hence neglecting $n_{2}$ in the denominator we have

$$ \begin{align*} \frac{p_{1}^{0}-p_{1}}{p_{1}^{0}} & =\frac{n_{2}}{n_{1}} \tag{2.27}\\ \text { or } \frac{p_{1}^{0}-p_{1}}{p_{1}^{0}} & =\frac{\mathrm{w_2} \times M_{1}}{M_{2} \times \mathrm{w_1}} \tag{2.28} \end{align*} $$

Here $w_{1}$ and $w_{2}$ are the masses and $M_{1}$ and $M_{2}$ are the molar masses of the solvent and solute respectively.

From this equation (2.28), knowing all other quantities, the molar mass of solute (M2) can be calculated.

Example 2.6

The vapour pressure of pure benzene at a certain temperature is 0.850 bar. A non-volatile, non-electrolyte solid weighing $0.5 \mathrm{~g}$ when added to $39.0 \mathrm{~g}$ of benzene (molar mass $78 \mathrm{~g} \mathrm{~mol}^{-1}$ ). Vapour pressure of the solution, then, is 0.845 bar. What is the molar mass of the solid substance?

Solution

The various quantities known to us are as follows:

$p_{1}{ }^{0}=0.850$ bar; $p=0.845 \mathrm{bar} ; M_{1}=78 \mathrm{~g} \mathrm{~mol}^{-1} ; w_{2}=0.5 \mathrm{~g} ; w_{1}=39 \mathrm{~g}$

Substituting these values in equation (2.28), we get

$\frac{0.850 \text { bar }-0.845 \text { bar }}{0.850 \text { bar }}=\frac{0.5 \mathrm{~g} \times 78 \mathrm{~g} \mathrm{~mol}^{-1}}{M_{2} \times 39 \mathrm{~g}}$

Therefore, $M_{2}=170 \mathrm{~g} \mathrm{~mol}^{-1}$

2.6.2 Elevation of Boiling Point

The vapour pressure of a liquid increases with increase of temperature. It boils at the temperature at which its vapour pressure is equal to the atmospheric pressure. For example, water boils at $373.15 \mathrm{~K}\left(100^{\circ} \mathrm{C}\right)$ because at this temperature the vapour pressure of water is 1.013 bar ( 1 atmosphere). We have also learnt in the last section that vapour pressure of the solvent decreases in the presence of non-volatile solute. Fig. 2.7 depicts the variation of vapour pressure of the pure solvent and solution as a function of temperature. For example, the vapour pressure of an aqueous solution of sucrose is less than 1.013 bar at $373.15 \mathrm{~K}$. In order to make this solution boil, its vapour pressure must be increased to 1.013 bar by raising the temperature above the boiling temperature of the pure solvent (water). Thus, the boiling point of a solution is prepared as shown in Fig. 2.7: The vapour pressure curve for solution lies below the curve for pure water. The diagram shows that $\Delta T_{\mathrm{b}}$ denotes the elevation of boiling point of a solvent in solution. always higher than that of the boiling point of the pure solvent in which the solution is prepared as shown in Fig. 2.7. Similar to lowering of vapour pressure, the elevation of boiling point also depends on the number of solute molecules rather than their nature. A solution of $1 \mathrm{~mol}$ of sucrose in $1000 \mathrm{~g}$ of water boils at $373.52 \mathrm{~K}$ at one atmospheric pressure.

Let $T_{\mathrm{b}}^{0}$ be the boiling point of pure solvent and $T_{\mathrm{b}}$ be the boiling point of solution. The increase in the boiling point $\Delta T_{\mathrm{b}}=T_{\mathrm{b}}-T_{\mathrm{b}}^{0}$ is known as elevation of boiling point.

Experiments have shown that for dilute solutions the elevation of boiling point $\left(\Delta T_{\mathrm{b}}\right)$ is directly proportional to the molal concentration of the solute in a solution. Thus

$$ \begin{align*} & \Delta T_{\mathrm{b}} \propto \mathrm{m} \tag{2.29}\\ \text { or } \quad \Delta T_{\mathrm{b}} & =K_{\mathrm{b}} \mathrm{m} \tag{2.30} \end{align*} $$

Here $m$ (molality) is the number of moles of solute dissolved in $1 \mathrm{~kg}$ of solvent and the constant of proportionality, $K_{\mathrm{b}}$ is called Boiling Point Elevation Constant or Molal Elevation Constant (Ebullioscopic Constant). The unit of $K_{\mathrm{b}}$ is $\mathrm{K} \mathrm{kg} \mathrm{mol}^{-1}$. Values of $K_{\mathrm{b}}$ for some common solvents are given in Table 1.3. If $\mathrm{w_2}$ gram of solute of molar mass $M_{2}$ is dissolved in $\mathrm{w_1}$ gram of solvent, then molality, $\mathrm{m}$ of the solution is given by the expression:

$$ \begin{equation*} \mathrm{m}=\frac{w_{2} / \mathrm{M_2}}{w_{1} / 1000}=\frac{1000 \times w_{2}}{M_{2} \times w_{1}} \tag{2.31} \end{equation*} $$

Substituting the value of molality in equation (1.30) we get

$$ \begin{align*} \Delta T_{\mathrm{b}} & =\frac{K_{\mathrm{b}} \times 1000 \times w_{2}}{M_{2} \times w_{1}} \tag{2.32}\\ M_{2} & =\frac{1000 \times w_{2} \times K_{\mathrm{b}}}{\Delta T_{\mathrm{b}} \times w_{1}} \tag{2.33} \end{align*} $$

Thus, in order to determine $M_{2}$, molar mass of the solute, known mass of solute in a known mass of the solvent is taken and $\Delta T_{\mathrm{b}}$ is determined experimentally for a known solvent whose $K_{\mathrm{b}}$ value is known.

2.6.3 Depression of Freezing Point

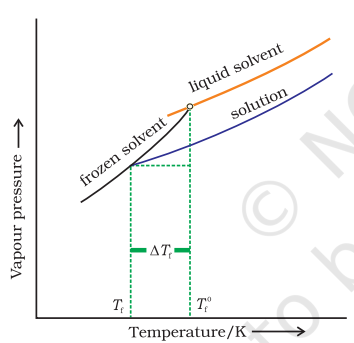
The lowering of vapour pressure of a solution causes a lowering of the freezing point compared to that of the pure solvent (Fig. 2 8). We know that at the freezing point of a substance, the solid phase is in dynamic equilibrium with the liquid phase. Thus, the freezing point of a substance may be defined as the temperature at which the vapour pressure of the substance in its liquid phase is equal to its vapour pressure in the solid phase. A solution will freeze when its vapour pressure equals the vapour pressure of the pure solid solvent as is clear from Fig. 2.8. According to Raoult’s law, when a non-volatile solid is added to the solvent its vapour pressure decreases and now it would become equal to that of solid solvent at lower temperature. Thus, the freezing point of the solvent decreases.

Let $T_{\mathrm{f}}^{0}$ be the freezing point of pure solvent and $T_{\mathrm{f}}$ be its freezing point when non-volatile solute is dissolved in it. The decrease in freezing point.

$$ \Delta T_{\mathrm{f}}=T_{\mathrm{f}}^{0}-T_{\mathrm{f}} \text { is known as depression in } $$

freezing point.

Similar to elevation of boiling point, depression of freezing point $\left(\Delta T_{\mathrm{f}}\right)$ for dilute solution (ideal solution) is directly proportional to molality, $\mathrm{m}$ of the solution. Thus,

$$ \Delta T_{\mathrm{f}} \propto \mathrm{m} $$

$$ \begin{equation*} \text { or } \quad \Delta T_{\mathrm{f}}=K_{\mathrm{f}} \mathrm{m} \tag{2.34} \end{equation*} $$

The proportionality constant, $\mathrm{K_\mathrm{f}}$, which depends on the nature of the solvent is known as Freezing Point Depression Constant or Molal

Depression Constant or Cryoscopic Constant. The unit of $\mathrm{K_\mathrm{f}}$ is $\mathrm{K} \mathrm{kg}$ $\mathrm{mol}^{-1}$. Values of $K_{\mathrm{f}}$ for some common solvents are listed in Table 2.3.

If $\mathrm{w_2}$ gram of the solute having molar mass as $M_{2}$, present in $\mathrm{w_1}$ gram of solvent, produces the depression in freezing point $\Delta T_{\mathrm{f}}$ of the solvent then molality of the solute is given by the equation (2.31).

$$ \begin{equation*} \mathrm{m}=\frac{w_{2} / M_{2}}{w_{1} / 1000} \tag{2.31} \end{equation*} $$

Substituting this value of molality in equation (2.34) we get:

$$ \begin{align*} \Delta T_{\mathrm{f}} & =\frac{K_{\mathrm{f}} \times w_{2} / M_{2}}{w_{1} / 1000} \\ \Delta T_{\mathrm{f}} & =\frac{K_{\mathrm{f}} \times w_{2} \times 1000}{M_{2} \times w_{1}} \tag{2.35}\\ M_{2} & =\frac{K_{\mathrm{f}} \times w_{2} \times 1000}{\Delta T_{\mathrm{f}} \times w_{1}} \tag{2.36} \end{align*} $$

Thus for determining the molar mass of the solute we should know the quantities $\mathrm{w_1}, \mathrm{w_2}, \Delta T_{\mathrm{f}}$, along with the molal freezing point depression constant. The values of $K_{f}$ and $K_{b}$, which depend upon the nature of the solvent, can be ascertained from the following relations.

$$ \begin{align*} K_{\mathrm{f}} & =\frac{R \times M_{1} \times T_{\mathrm{f}}^{2}}{1000 \times \Delta_{\text {fus }} H} \tag{2.37}\\ K_{\mathrm{b}} & =\frac{R \times M_{1} \times T_{\mathrm{b}}^{2}}{1000 \times \Delta_{\text {vap }} H} \tag{2.38} \end{align*} $$

Here the symbols $R$ and $M_{1}$ stand for the gas constant and molar mass of the solvent, respectively and $T_{\mathrm{f}}$ and $T_{\mathrm{b}}$ denote the freezing point and the boiling point of the pure solvent respectively in kelvin. Further, $\Delta_{\text {fus }} H$ and $\Delta_{\text {vap }} H$ represent the enthalpies for the fusion and vapourisation of the solvent, respectively.

2.6.4 Osmosis and Osmotic Pressure

There are many phenomena which we observe in nature or at home. For example, raw mangoes shrivel when pickled in brine (salt water); wilted flowers revive when placed in fresh water, blood cells collapse when suspended in saline water, etc. If we look into these processes we find one thing common in all, that is, all these substances are bound by membranes. These membranes can be of animal or vegetable origin and these occur naturally such as pig’s bladder or parchment or can be synthetic such as cellophane. These membranes appear to be continuous sheets or films, yet they contain a network of submicroscopic holes or pores. Small solvent molecules, like water, can pass through these holes but the passage of bigger molecules like solute is hindered. Membranes having this kind of properties are known as semipermeable membranes (SPM).

Assume that only solvent molecules can pass through these semipermeable membranes. If this membrane is placed between the solvent and solution as shown in Fig. 2.9, the solvent molecules will flow through the membrane from pure solvent to the solution. This process of flow of the solvent is called osmosis.

The flow will continue till the equilibrium is attained. The flow of the solvent from its side to solution side across a semipermeable membrane can be stopped if some extra pressure is applied on the solution. This pressure that just stops the flow of solvent is called osmotic pressure of the solution. The flow of solvent from dilute solution to the concentrated solution across a semipermeable membrane is due to osmosis. The important point to be kept in mind is that solvent molecules always flow from lower concentration to higher concentration of solution. The osmotic pressure has been found to depend on the concentration of the solution.

The osmotic pressure of a solution is the excess pressure that must be applied to a solution to prevent osmosis, i.e., to stop the passage of solvent molecules through a semipermeable membrane into the solution. This is illustrated in Fig. 2.10. Osmotic pressure is a colligative property as it depends on the number of solute molecules and not on their identity. For dilute solutions, it has been found experimentally that osmotic pressure is proportional to the molarity, C of the solution at a given temperature T. Thus:

$$ \begin{equation*} \Pi=C R T \tag{2.39} \end{equation*} $$

Here $\Pi$ is the osmotic pressure and $\mathrm{R}$ is the gas constant.

$$ \begin{equation*} \Pi=\left(n_{2} / V\right) R T \tag{2.40} \end{equation*} $$

Here $V$ is volume of a solution in litres containing $\mathrm{n_2}$ moles of solute. If $\mathrm{w_2}$ grams of solute, of molar mass, $M_{2}$ is present in the solution, then $n_{2}=\mathrm{w_2} / M_{2}$ and we can write,

$$ \begin{array}{r} \Pi V=\frac{\mathbf{w_2} R T}{M_{2}} \\ \text { or } M_{2}=\frac{\mathbf{w_2} R T}{\Pi V} \tag{2.42} \end{array} $$

Thus, knowing the quantities $\mathrm{w_2}, T, \Pi$ and $V$ we can calculate the molar mass of the solute.

Measurement of osmotic pressure provides another method of determining molar masses of solutes. This method is widely used to determine molar masses of proteins, polymers and other macromolecules. The osmotic pressure method has the advantage over other methods as pressure measurement is around the room temperature and the molarity of the solution is used instead of molality. As compared to other colligative properties, its magnitude is large even for very dilute solutions. The technique of osmotic pressure for determination of molar mass of solutes is particularly useful for biomolecules as they are generally not stable at higher temperatures and polymers have poor solubility.

Two solutions having same osmotic pressure at a given temperature are called isotonic solutions. When such solutions are separated by semipermeable membrane no osmosis occurs between them. For example, the osmotic pressure associated with the fluid inside the blood cell is equivalent to that of 0.9% (mass/ volume) sodium chloride solution, called normal saline solution and it is safe to inject intravenously. On the other hand, if we place the cells in a solution containing more than 0.9% (mass/volume) sodium chloride, water will flow out of the cells and they would shrink. Such a solution is called hypertonic. If the salt concentration is less than 0.9% (mass/volume), the solution is said to be hypotonic. In this case, water will flow into the cells if placed in this solution and they would swell.

The phenomena mentioned in the beginning of this section can be explained on the basis of osmosis. A raw mango placed in concentrated salt solution loses water via osmosis and shrivel into pickle. Wilted flowers revive when placed in fresh water. A carrot that has become limp because of water loss into the atmosphere can be placed into the water making it firm once again. Water will move into its cells through osmosis. When placed in water containing less than 0.9% (mass/ volume) salt, blood cells swell due to flow of water in them by osmosis. People taking a lot of salt or salty food experience water retention in tissue cells and intercellular spaces because of osmosis. The resulting puffiness or swelling is called edema. Water movement from soil into plant roots and subsequently into upper portion of the plant is partly due to osmosis. The preservation of meat by salting and of fruits by adding sugar protects against bacterial action. Through the process of osmosis, a bacterium on salted meat or candid fruit loses water, shrivels and dies.

2.6.5 Reverse Osmosis and Water Purification

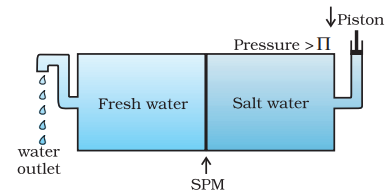
The direction of osmosis can be reversed if a pressure larger than the osmotic pressure is applied to the solution side. That is, now the pure solvent flows out of the solution through the semi permeable membrane. This phenomenon is called reverse osmosis and is of great practical utility. Reverse osmosis is used in desalination of sea water. A schematic set up for the process is shown in Fig. 2.11. When pressure more than osmotic pressure is applied, pure water is squeezed out of the sea water through the membrane. A variety of polymer membranes are available for this purpose.

The pressure required for the reverse osmosis is quite high. A workable porous membrane is a film of cellulose acetate placed over a suitable support. Cellulose acetate is permeable to water but impermeable to impurities and ions present in sea water. These days many countries use desalination plants to meet their potable water requirements.

Summary

A solution is a homogeneous mixture of two or more substances. Solutions are classified as solid, liquid and gaseous solutions. The concentration of a solution is expressed in terms of mole fraction, molarity, molality and in percentages. The dissolution of a gas in a liquid is governed by Henry’s law, according to which, at a given temperature, the solubility of a gas in a liquid is directly proportional to the partial pressure of the gas. The vapour pressure of the solvent is lowered by the presence of a non-volatile solute in the solution and this lowering of vapour pressure of the solvent is governed by Raoult’s law, according to which the relative lowering of vapour pressure of the solvent over a solution is equal to the mole fraction of a non-volatile solute present in the solution. However, in a binary liquid solution, if both the components of the solution are volatile then another form of Raoult’s law is used. Mathematically, this form of the Raoult’s law is stated as: $p_{\text {total }}=p_{1}^{0} x_{1}+p_{2}^{0} x_{2}$. Solutions which obey Raoult’s law over the entire range of concentration are called ideal solutions. Two types of deviations from Raoult’s law, called positive and negative deviations are observed. Azeotropes arise due to very large deviations from Raoult’s law.

The properties of solutions which depend on the number of solute particles and are independent of their chemical identity are called colligative properties. These are lowering of vapour pressure, elevation of boiling point, depression of freezing point and osmotic pressure. The process of osmosis can be reversed if a pressure higher than the osmotic pressure is applied to the solution. Colligative properties have been used to determine the molar mass of solutes. Solutes which dissociate in solution exhibit molar mass lower than the actual molar mass and those which associate show higher molar mass than their actual values.

Quantitatively, the extent to which a solute is dissociated or associated can be expressed by van’t Hoff factor i. This factor has been defined as ratio of normal molar mass to experimentally determined molar mass or as the ratio of observed colligative property to the calculated colligative property.

Exercises

2.1 Define the term solution. How many types of solutions are formed? Write briefly about each type with an example.

Answer

Homogeneous mixtures of two or more than two components are known as solutions.

There are three types of solutions.

(i) Gaseous solution:

The solution in which the solvent is a gas is called a gaseous solution. In these solutions, the solute may be liquid, solid, or gas. For example, a mixture of oxygen and nitrogen gas is a gaseous solution.

(ii) Liquid solution:

The solution in which the solvent is a liquid is known as a liquid solution. The solute in these solutions may be gas, liquid, or solid.

For example, a solution of ethanol in water is a liquid solution.

(iii) Solid solution:

The solution in which the solvent is a solid is known as a solid solution. The solute may be gas, liquid or solid. For example, a solution of copper in gold is a solid solution.

2.2 Give an example of a solid solution in which the solute is a gas.

Answer

In case a solid solution is formed between two substances (one having very large particles and the other having very small particles), an interstitial solid solution will be formed. For example, a solution of hydrogen in palladium is a solid solution in which the solute is a gas.

2.3 Define the following terms:

(i) Mole fraction

(ii) Molality

(iii) Molarity

(iv) Mass percentage.

Answer

(i) Mole fraction:

The mole fraction of a component in a mixture is defined as the ratio of the number of moles of the component to the total number of moles of all the components in the mixture.

i.e.,

$$ \text{Mole fraction of a component }=\frac{\text { Number of moles of the component }}{\text { Total number of moles of all components }} $$

Mole fraction is denoted by ’ $x$ ‘.

If in a binary solution, the number of moles of the solute and the solvent are $n_{A}$ and $n_{B}$ respectively, then the mole fraction of the solute in the solution is given by,

$x_{A}=\frac{n_{A}}{n_{A}+n_{B}}$

Similarly, the mole fraction of the solvent in the solution is given as:

$x_{B}=\frac{n_{B}}{n_{A}+n_{B}}$

(ii) Molality

Molality (m) is defined as the number of moles of the solute per kilogram of the solvent. It is expressed as:

$\text{Molality (m)}=\frac{\text { Moles of solute }}{\text { Mass of solvent in } \mathrm{kg}}$

(iii) Molarity

Molarity $(M)$ is defined as the number of moles of the solute dissolved in one Litre of the solution.

It is expressed as:

Molarity (M) $=\frac{\text { Moles of solute }}{\text { Volume of solution in Litre }}$

(iv) Mass percentage:

The mass percentage of a component of a solution is defined as the mass of the solute in grams present in $100 \mathrm{~g}$ of the solution. It is expressed as:

$$ \text{Mass $\%$ of a component }=\frac{\text { Mass of component in solution }}{\text { Total mass of solution }} \times 100 $$

2.4 Concentrated nitric acid used in laboratory work is $68 \%$ nitric acid by mass in aqueous solution. What should be the molarity of such a sample of the acid if the density of the solution is $1.504 \mathrm{~g} \mathrm{~mL}^{-1}$ ?

Answer

Concentrated nitric acid used in laboratory work is $68 \%$ nitric acid by mass in an aqueous solution. This means that $68 \mathrm{~g}$ of nitric acid is dissolved in $100 \mathrm{~g}$ of the solution.

Molar mass of nitric acid $\left(\mathrm{HNO_3}\right)=1 \times 1+1 \times 14+3 \times 16=63 \mathrm{~g} \mathrm{~mol}^{-1}$

Then, number of moles of $\mathrm{HNO_3}=\frac{68}{63} \mathrm{~mol}$

$=1.079 \mathrm{~mol}$

Given,

Density of solution $=1.504 \mathrm{~g} \mathrm{~mL}^{-1}$

$\therefore$ Volume of $100 \mathrm{~g}$ solution $=\frac{100}{1.504} \mathrm{~mL}$

$=66.49 \mathrm{~mL}$

$=66.49 \times 10^{-3} \mathrm{~L}$

Molarity of solution $=\frac{1.079 \mathrm{~mol}}{66.49 \times 10^{-3} \mathrm{~L}}$

$=16.23 \mathrm{M}$

2.5 A solution of glucose in water is labelled as $10 \% \mathrm{w} / \mathrm{w}$, what would be the molality and mole fraction of each component in the solution? If the density of solution is $1.2 \mathrm{~g} \mathrm{~mL}^{-1}$, then what shall be the molarity of the solution?

Answer

$10 \% \mathrm{w} / \mathrm{w}$ solution of glucose in water means that $10 \mathrm{~g}$ of glucose in present in $100 \mathrm{~g}$ of the solution i.e., $10 \mathrm{~g}$ of glucose is present in $(100-10) \mathrm{g}=90 \mathrm{~g}$ of water.

Molar mass of glucose $\left(\mathrm{C_6} \mathrm{H_12} \mathrm{O_6}\right)=6 \times 12+12 \times 1+6 \times 16=180 \mathrm{~g} \mathrm{~mol}^{-1}$

$$ \text{Then, number of moles of glucose }=\frac{10}{180} \mathrm{~mol} $$

$=0.056 \mathrm{~mol}$

$\therefore$ Molality of solution $\quad=\frac{0.056 \mathrm{~mol}}{0.09 \mathrm{~kg}}=0.62 \mathrm{~m}$

Number of moles of water $=\frac{90 \mathrm{~g}}{18 \mathrm{~g} \mathrm{~mol}^{-1}}$

$=5 \mathrm{~mol}$

$$ \begin{aligned} \Rightarrow \text { Mole fraction of glucose } \left(x_{\mathrm{g}}\right) & =\frac{0.056}{0.056+5} \\ \quad & =0.011 \end{aligned} $$

And, mole fraction of water $x_{\mathrm{w}}=1-x_{\mathrm{g}}$

$=1-0.011$

$=0.989$

If the density of the solution is $1.2 \mathrm{~g} \mathrm{~mL}^{-1}$, then the volume of the $100 \mathrm{~g}$ solution can be given as:

$=\frac{100 \mathrm{~g}}{1.2 \mathrm{~g} \mathrm{~mL}^{-1}}$

$=83.33 \mathrm{~mL}$

$=83.33 \times 10^{-3} \mathrm{~L}$

$\therefore$ Molarity of the solution $=\frac{0.056 \mathrm{~mol}}{83.33 \times 10^{-3} \mathrm{~L}}$

$=0.67 \mathrm{M}$

2.6 How many $\mathrm{mL}$ of $0.1 \mathrm{M} \mathrm{HCl}$ are required to react completely with $1 \mathrm{~g}$ mixture of $\mathrm{Na_2} \mathrm{CO_3}$ and $\mathrm{NaHCO_3}$ containing equimolar amounts of both?

Answer

Let the amount of $\mathrm{Na_2} \mathrm{CO_3}$ in the mixture be $x \mathrm{~g}$.

Then, the amount of $\mathrm{NaHCO_3}$ in the mixture is $(1-x) \mathrm{g}$.

Molar mass of $\mathrm{Na_2} \mathrm{CO_3}=2 \times 23+1 \times 12+3 \times 16$

$=106 \mathrm{~g} \mathrm{~mol}^{-1}$

$\therefore$ Number of moles $\mathrm{Na_2} \mathrm{CO_3}=\frac{x}{106} \mathrm{~mol}$

Molar mass of $\mathrm{NaHCO_3}=1 \times 23+1 \times 1 \times 12+3 \times 16$

$=84 \mathrm{~g} \mathrm{~mol}^{-1}$

$\therefore$ Number of moles of $\mathrm{NaHCO_3}=\frac{1-x}{84} \mathrm{~mol}$

According to the question,

$\frac{x}{106}=\frac{1-x}{84}$

$\Rightarrow 84 x=106-106 x$

$\Rightarrow 190 x=106$

$\Rightarrow x=0.5579$

Therefore, number of moles of $\mathrm{Na_2} \mathrm{CO_3}=\frac{0.5579}{106} \mathrm{~mol}$

$=0.0053 \mathrm{~mol}$

And, number of moles of $\mathrm{NaHCO_3}=\frac{1-0.5579}{84}$ $=0.0053 \mathrm{~mol}$

$\mathrm{HCl}$ reacts with $\mathrm{Na_2} \mathrm{CO_3}$ and $\mathrm{NaHCO_3}$ according to the following equation.

$\underset{\mathrm{2~mol}}{2 \mathrm{HCl}}+ \underset{\mathrm{1~mol}}{\mathrm{Na_2} \mathrm{CO_3}} \longrightarrow 2 \mathrm{NaCl}+\mathrm{H_2} \mathrm{O}+\mathrm{CO_2}$

$\underset{\mathrm{1~mol}}{\mathrm{HCl}}+\underset{\mathrm{1~mol}}{\mathrm{NaHCO_3}} \longrightarrow \mathrm{NaCl}+\mathrm{H_2} \mathrm{O}+\mathrm{CO_2}$

$1 \quad 1 $

1 mol of $\mathrm{Na_2} \mathrm{CO_3}$ reacts with $2 \mathrm{~mol}$ of $\mathrm{HCl}$.

Therefore, $0.0053 \mathrm{~mol}$ of $\mathrm{Na_2} \mathrm{CO_3}$ reacts with $2 \times 0.0053 \mathrm{~mol}=0.0106 \mathrm{~mol}$.

Similarly, 1 mol of $\mathrm{NaHCO_3}$ reacts with $1 \mathrm{~mol}$ of $\mathrm{HCl}$.

Therefore, $0.0053 \mathrm{~mol}$ of $\mathrm{NaHCO_3}$ reacts with $0.0053 \mathrm{~mol}$ of $\mathrm{HCl}$.

Total moles of $\mathrm{HCl}$ required $=(0.0106+0.0053) \mathrm{mol}$

$=0.0159 \mathrm{~mol}$

In $0.1 \mathrm{M}$ of $\mathrm{HCl}$,

$0.1 \mathrm{~mol}$ of $\mathrm{HCl}$ is preset in $1000 \mathrm{~mL}$ of the solution.

Therefore, $0.0159 \mathrm{~mol}$ of $\mathrm{HCl}$ is present in

$$ \frac{1000 \times 0.0159}{0.1} \mathrm{~mol} $$

$=159 \mathrm{~mL}$ of the solution

Hence, $159 \mathrm{~mL}$ of $0.1 \mathrm{M}$ of $\mathrm{HCl}$ is required to react completely with $1 \mathrm{~g}$ mixture of $\mathrm{Na_2} \mathrm{CO_3}$ and $\mathrm{NaHCO_3,}$, containing equimolar amounts of both.

2.7 A solution is obtained by mixing $300 \mathrm{~g}$ of $25 \%$ solution and $400 \mathrm{~g}$ of $40 \%$ solution by mass. Calculate the mass percentage of the resulting solution.

Answer

Total amount of solute present in the mixture is given by,

$300 \times \frac{25}{100}+400 \times \frac{40}{100}$

$=75+160$

$=235 \mathrm{~g}$

Total amount of solution $=300+400=700 \mathrm{~g}$

Therefore, mass percentage (w/w) of the solute in the resulting solution,

$$ =\frac{235}{700} \times 100 \% $$

$=33.57 \%$

And, mass percentage ( $w / w$ ) of the solvent in the resulting solution,

$=(100-33.57) \%$

$=66.43 \%$

2.8 An antifreeze solution is prepared from $222.6 \mathrm{~g}$ of ethylene glycol $\left(\mathrm{C_2} \mathrm{H_6} \mathrm{O_2}\right)$ and $200 \mathrm{~g}$ of water. Calculate the molality of the solution. If the density of the solution is $1.072 \mathrm{~g} \mathrm{~mL}^{-1}$, then what shall be the molarity of the solution?

Answer

Molar mass of ethylene glycol $\left[\mathrm{C_2} \mathrm{H_4}(\mathrm{OH})_{2}\right]=2 \times 12+6 \times 1+2 \times 16$

$=62 \mathrm{gmol}^{-1}$

Number of moles of ethylene glycol

$$ =\frac{222.6 \mathrm{~g}}{62 \mathrm{gmol}^{-1}} $$

$=3.59 \mathrm{~mol}$

Therefore, molality of the solution

$$ =\frac{3.59 \mathrm{~mol}}{0.200 \mathrm{~kg}} $$

$=17.95 \mathrm{~m}$

Total mass of the solution $=(222.6+200) \mathrm{g}$

$=422.6 \mathrm{~g}$

Given,

Density of the solution $=1.072 \mathrm{~g} \mathrm{~mL}^{-1}$

$\therefore$ Volume of the solution $=\frac{422.6 \mathrm{~g}}{1.072 \mathrm{~g} \mathrm{~mL}^{-1}}$

$=394.22 \mathrm{~mL}$

$=0.3942 \times 10^{-3} \mathrm{~L}$

$\Rightarrow$ Molarity of the solution $=\frac{3.59 \mathrm{~mol}}{0.39422 \times 10^{-3} \mathrm{~L}}$

$=9.11 \mathrm{M}$

2.9 A sample of drinking water was found to be severely contaminated with chloroform $\left(\mathrm{CHCl_3}\right)$ supposed to be a carcinogen. The level of contamination was 15 ppm (by mass):

(i) express this in percent by mass

(ii) determine the molality of chloroform in the water sample.

Answer

(i) 15 ppm (by mass) means 15 parts per million $\left(10^{6}\right)$ of the solution.

Therefore, percent by mass $=\frac{15}{10^{6}} \times 100 \%$

$=1.5 \times 10^{-3} \%$

(ii) Molar mass of chloroform $\left(\mathrm{CHCl_3}\right)=1 \times 12+1 \times 1+3 \times 35.5$

$=119.5 \mathrm{~g} \mathrm{~mol}^{-1}$

Now, according to the question,

$15 \mathrm{~g}$ of chloroform is present in $10^{6} \mathrm{~g}$ of the solution.

i.e., $15 \mathrm{~g}$ of chloroform is present in $\left(10^{6}-15\right) /10^{6} \mathrm{~g}$ of water.

$\therefore$ Molality of the solution $=\frac{\frac{15}{119.5} \mathrm{~mol}}{10^{6} \times 10^{-3} \mathrm{~kg}}$

$=1.26 \times 10^{-4} \mathrm{~m}$

2.10 What role does the molecular interaction play in a solution of alcohol and water?

Answer

In pure alcohol and water, the molecules are held tightly by a strong hydrogen bonding. The interaction between the molecules of alcohol and water is weaker than alcohol-alcohol and water-water interactions. As a result, when alcohol and water are mixed, the intermolecular interactions become weaker and the molecules can easily escape. This increases the vapour pressure of the solution, which in turn lowers the boiling point of the resulting solution.

2.11 Why do gases always tend to be less soluble in liquids as the temperature is raised?

Answer

Solubility of gases in liquids decreases with an increase in temperature. This is because dissolution of gases in liquids is an exothermic process.

Gas + Liquid $\longrightarrow$ Solution + Heat

Therefore, when the temperature is increased, heat is supplied and the equilibrium shifts backwards, thereby decreasing the solubility of gases.

2.12 State Henry’s law and mention some important applications.

Answer

Henry’s law states that partial pressure of a gas in the vapour phase is proportional to the mole fraction of the gas in the solution. If $p$ is the partial pressure of the gas in the vapour phase and $x$ is the mole fraction of the gas, then Henry’s law can be expressed as:

$p=K_{\mathrm{H}} x$

Where,

$K_{\mathrm{H}}$ is Henry’s law constant

Some important applications of Henry’s law are mentioned below.

(i) Bottles are sealed under high pressure to increase the solubility of $\mathrm{CO_2}$ in soft drinks and soda water.

(ii) Henry’s law states that the solubility of gases increases with an increase in pressure. Therefore, when a scuba diver dives deep into the sea, the increased sea pressure causes the nitrogen present in air to dissolve in his blood in great amounts. As a result, when he comes back to the surface, the solubility of nitrogen again decreases and the dissolved gas is released, leading to the formation of nitrogen bubbles in the blood. This results in the blockage of capillaries and leads to a medical condition known as ‘bends’ or ‘decompression sickness’.

Hence, the oxygen tanks used by scuba divers are filled with air and diluted with helium to avoid bends.

(iii) The concentration of oxygen is low in the blood and tissues of people living at high altitudes such as climbers. This is because at high altitudes, partial pressure of oxygen is less than that at ground level. Low-blood oxygen causes climbers to become weak and disables them from thinking clearly. These are symptoms of anoxia.

2.13 The partial pressure of ethane over a solution containing $6.56 \times 10^{-3} \mathrm{~g}$ of ethane is 1 bar. If the solution contains $5.00 \times 10^{-2} \mathrm{~g}$ of ethane, then what shall be the partial pressure of the gas?

Answer

Molar mass of ethane $\left(\mathrm{C_2} \mathrm{H_6}\right)=2 \times 12+6 \times 1$

$=30 \mathrm{~g} \mathrm{~mol}^{-1}$

$\therefore$ Number of moles present in $6.56 \times 10^{-3} \mathrm{~g}$ of ethane $=\frac{6.56 \times 10^{-3}}{30}$

$=2.187 \times 10^{-4} \mathrm{~mol}$

Let the number of moles of the solvent be $x$.

According to Henry’s law,

$$ \begin{aligned} & p=K_{H} X \\ & \Rightarrow 1 \text { bar }=K_{H} \cdot \frac{2.187 \times 10^{-4}}{2.187 \times 10^{-4}+x} \\ & \Rightarrow 1 \text { bar }=K_{H} \cdot \frac{2.187 \times 10^{-4}}{x}\left(\text { Since } x > > 2.187 \times 10^{-4}\right) \\ & \Rightarrow K_{H}=\frac{x}{2.187 \times 10^{-4}} \text { bar } \end{aligned} $$

2.14 What is meant by positive and negative deviations from Raoult’s law and how is the sign of $\Delta_{\text {mix }} \mathrm{H}$ related to positive and negative deviations from Raoult’s law?

Answer

According to Raoult’s law, the partial vapour pressure of each volatile component in any solution is directly proportional to its mole fraction. The solutions which obey Raoult’s law over the entire range of concentration are known as ideal solutions. The solutions that do not obey Raoult’s law (non-ideal solutions) have vapour pressures either higher or lower than that predicted by Raoult’s law. If the vapour pressure is higher, then the solution is said to exhibit positive deviation, and if it is lower, then the solution is said to exhibit negative deviation from Raoult’s law.

Vapour pressure of a two-component solution showing positive deviation from Raoult’s law

Vapour pressure of a two-component solution showing negative deviation from Raoult’s law

In the case of an ideal solution, the enthalpy of the mixing of the pure components for forming the solution is zero.

$\Delta_{\text {sol }} H=0$

In the case of solutions showing positive deviations, absorption of heat takes place.

$\therefore \Delta_{\text {sol }} H=$ Positive

In the case of solutions showing negative deviations, evolution of heat takes place.

$\therefore \Delta_{\text {sol }} H=$ Negative

2.15 An aqueous solution of $2 \%$ non-volatile solute exerts a pressure of 1.004 bar at the normal boiling point of the solvent. What is the molar mass of the solute?

Answer

Here,

Vapour pressure of the solution at normal boiling point $\left(p_{1}\right)=1.004$ bar

Vapour pressure of pure water at normal boiling point $\left(p_{1}^{0}\right)=1.013$ bar

Mass of solute, $\left(w_{2}\right)=2 \mathrm{~g}$

Mass of solvent (water), $\left(w_{1}\right)=98 \mathrm{~g}$

Molar mass of solvent (water), $\left(M_{1}\right)=18 \mathrm{~g} \mathrm{~mol}^{-1}$

According to Raoult’s law,

$\frac{p_{1}^{0}-p_{1}}{p_{1}^{0}}=\frac{w_{2} \times M_{1}}{M_{2} \times w_{1}}$

$\Rightarrow \frac{1.013-1.004}{1.013}=\frac{2 \times 18}{M_{2} \times 98}$

$\Rightarrow \frac{0.009}{1.013}=\frac{2 \times 18}{M_{2} \times 98}$

$\Rightarrow M_{2}=\frac{1.013 \times 2 \times 18}{0.009 \times 98}$

$=41.35 \mathrm{~g} \mathrm{~mol}^{-1}$

Hence, the molar mass of the solute is $41.35 \mathrm{~g} \mathrm{~mol}^{-1}$.

2.16 Heptane and octane form an ideal solution. At $373 \mathrm{~K}$, the vapour pressures of the two liquid components are $105.2 \mathrm{kPa}$ and $46.8 \mathrm{kPa}$ respectively. What will be the vapour pressure of a mixture of $26.0 \mathrm{~g}$ of heptane and $35 \mathrm{~g}$ of octane?

Answer

Vapour pressure of heptane $\left(p_{1}^{0}\right)=105.2 \mathrm{kPa}$

Vapour pressure of octane $\left(p_{2}^{0}\right)=46.8 \mathrm{kPa}$

We know that,

Molar mass of heptane $\left(\mathrm{C_7} \mathrm{H_16}\right)=7 \times 12+16 \times 1$

$=100 \mathrm{~g} \mathrm{~mol}^{-1}$

$\therefore$ Number of moles of heptane $=\frac{26}{100} \mathrm{~mol}$

$=0.26 \mathrm{~mol}$

Molar mass of octane $\left(\mathrm{C_8} \mathrm{H_18}\right)=8 \times 12+18 \times 1$

$=114 \mathrm{~g} \mathrm{~mol}^{-1}$

$\therefore$ Number of moles of octane $=\frac{35}{114} \mathrm{~mol}$

$=0.31 \mathrm{~mol}$

Mole fraction of heptane, $x_{1}=\frac{0.26}{0.26+0.31}$

$=0.456$

And, mole fraction of octane, $x_{2}=1-0.456$

$=0.544$

Now, partial pressure of heptane, $p_{1}=x_{1} p_{1}^{0}$

$=0.456 \times 105.2$

$=47.97 \mathrm{kPa}$

Partial pressure of octane, $p_{2}=x_{2} p_{2}^{0}$

$=0.544 \times 46.8$

$=25.46 \mathrm{kPa}$

Hence, vapour pressure of solution, $p_{\text {total }}=p_{1}+p_{2}$

$=47.97+25.46$

$=73.43 \mathrm{kPa}$

1.17 The vapour pressure of water is $12.3 \mathrm{kPa}$ at $300 \mathrm{~K}$. Calculate vapour pressure of 1 molal solution of a non-volatile solute in it.

Answer

1 molal solution means $1 \mathrm{~mol}$ of the solute is present in $1000 \mathrm{~g}$ of the solvent (water).

Molar mass of water $=18 \mathrm{~g} \mathrm{~mol}^{-1}$

$\therefore$ Number of moles present in $1000 \mathrm{~g}$ of water $=\frac{1000}{18}$

$=55.56 \mathrm{~mol}$

Therefore, mole fraction of the solute in the solution is

$x_{2}=\frac{1}{1+55.56}=0.0177$

It is given that,

Vapour pressure of water, $p_{1}^{0}=12.3 \mathrm{kPa}$

Applying the relation, $\frac{p_{1}^{0}-p_{1}}{p_{1}^{0}}=x_{2}$

$\Rightarrow \frac{12.3-p_{1}}{12.3}=0.0177$

$\Rightarrow 12.3-p_{1}=0.2177$

$\Rightarrow p_{1}=12.0823$

$=12.08 \mathrm{kPa}$ (approximately)

Hence, the vapour pressure of the solution is $12.08 \mathrm{kPa}$.

2.18 Calculate the mass of a non-volatile solute (molar mass $40 \mathrm{~g} \mathrm{~mol}^{-1}$ ) which should be dissolved in $114 \mathrm{~g}$ octane to reduce its vapour pressure to $80 \%$.

Answer

Let the vapour pressure of pure octane be $p_{1}^{0}$.

Then, the vapour pressure of the octane after dissolving the non-volatile solute is $\frac{80}{100} p_{1}^{0}=0.8 p_{1}^{0}$.

Molar mass of solute, $M_{2}=40 \mathrm{~g} \mathrm{~mol}^{-1}$

Mass of octane, $w_{1}=114 \mathrm{~g}$

Molar mass of octane, $\left(\mathrm{C_8} \mathrm{H_18}\right), M_{1}=8 \times 12+18 \times 1$

$=114 \mathrm{~g} \mathrm{~mol}^{-1}$

Applying the relation,

$ \begin{aligned} & \frac{p_{1}^{0}-p_{1}}{p_{1}^{0}}=\frac{w_{2} \times M_{1}}{M_{2} \times w_{1}} \\ & \Rightarrow \frac{p_{1}^{0}-0.8 p_{1}^{0}}{p_{1}^{0}}=\frac{w_{2} \times 114}{40 \times 114} \end{aligned} $

$\Rightarrow \frac{0.2 p_{1}^{0}}{p_{1}^{0}}=\frac{w_{2}}{40}$

$\Rightarrow 0.2=\frac{w_{2}}{40}$

$\Rightarrow w_{2}=8 \mathrm{~g}$

Hence, the required mass of the solute is $8 \mathrm{~g}$.

2.19 A solution containing $30 \mathrm{~g}$ of non-volatile solute exactly in $90 \mathrm{~g}$ of water has a vapour pressure of $2.8 \mathrm{kPa}$ at $298 \mathrm{~K}$. Further, $18 \mathrm{~g}$ of water is then added to the solution and the new vapour pressure becomes $2.9 \mathrm{kPa}$ at $298 \mathrm{~K}$. Calculate:

(i) molar mass of the solute

(ii) vapour pressure of water at $298 \mathrm{~K}$.

Answer

(i) Let, the molar mass of the solute be $\mathrm{M} \mathrm{g} \mathrm{mol}^{-1}$

$$ n_{1}=\frac{90 \mathrm{~g}}{18 \mathrm{~g} \mathrm{~mol}^{-1}}=5 \mathrm{~mol} $$

Now, the no. of moles of solvent (water),

$$ n_{2}=\frac{30 \mathrm{~g}}{\mathrm{M} \mathrm{mol}^{-1}}=\frac{30}{\mathrm{M}} \mathrm{mol} $$

And, the no. of moles of solute,

$$ p_{1}=2.8 \mathrm{kPa} $$

Applying the relation:

$$ \begin{align*} & \frac{p_{1}^{0}-p_{1}}{p_{1}^{0}}=\frac{n_{2}}{n_{1}+n_{2}} \\ \\ & \Rightarrow \frac{p_{1}^{0}-2.8}{p_{1}^{0}}=\frac{\frac{30}{\mathrm{M}}}{5+\frac{30}{\mathrm{M}}} \\ \\ & \Rightarrow 1-\frac{2.8}{p_{1}^{0}}=\frac{\frac{30}{\mathrm{M}}+30}{\mathrm{M}} \\ \\ & \Rightarrow 1-\frac{2.8}{p_{1}^{0}}=\frac{30}{5 \mathrm{M}+30} \\ \\ & \Rightarrow \frac{2.8}{p_{1}^{0}}=1-\frac{30}{5 \mathrm{M}+30} \\ \\ & \Rightarrow \frac{2.8}{p_{1}^{0}}=\frac{5 \mathrm{M}+30-30}{5 \mathrm{M}+30} \\ \\ & \Rightarrow \frac{2.8}{p_{1}^{0}}=\frac{5 \mathrm{M}}{5 \mathrm{M}+30} \\ \\ & \Rightarrow \frac{p^{0}}{2.8} =\frac{5 \mathrm{M}+30}{5 \mathrm{M}} \tag{i} \\ \\ \end{align*} $$

After the addition of $18 \mathrm{~g}$ of water:

$$ \begin{aligned} & n_{1}=\frac{90+18 \mathrm{~g}}{18}=6 \mathrm{~mol} \\ & p_{1}=2.9 \mathrm{kPa} \end{aligned} $$

Again, applying the relation:

$$ \begin{align*} & \frac{p_{1}^{0}-p_{1}}{p_{1}^{0}}=\frac{n_{2}}{n_{1}+n_{2}} \\ \\ & \Rightarrow \frac{p_{1}^{0}-2.9}{p_{1}^{0}}=\frac{\frac{30}{\mathrm{M}}}{6+\frac{30}{\mathrm{M}}} \\ \\ & \Rightarrow 1-\frac{2.9}{p_{1}^{0}}=\frac{\frac{30}{\mathrm{M}}}{\frac{6 \mathrm{M}+30}{\mathrm{M}}} \\ \\ & \Rightarrow 1-\frac{2.9}{p_{1}^{0}}=\frac{30}{6 \mathrm{M}+30} \\ \\ & \Rightarrow \frac{2.9}{p_{1}^{0}}=1-\frac{30}{6 \mathrm{M}+30} \\ \\ & \Rightarrow \frac{2.9}{p_{1}^{0}}=\frac{6 \mathrm{M}+30-30}{6 \mathrm{M}+30} \\ \\ & \Rightarrow \frac{2.9}{p_{1}^{0}}=\frac{6 \mathrm{M}}{6 \mathrm{M}+30} \\ \\ & \Rightarrow \frac{p_{1}^{0}}{2.9}=\frac{6 \mathrm{M}+30}{6 \mathrm{M}} \tag{ii} \end{align*} $$

Dividing equation (i)by (ii), we have:

$$ \begin{aligned} & \frac{2.9}{2.8}=\frac{\frac{5 \mathrm{M}+30}{5 \mathrm{M}}}{\frac{6 \mathrm{M}+30}{6 \mathrm{M}}} \\ \\ & \Rightarrow \frac{2.9}{2.8} \times \frac{6 \mathrm{M}+30}{6}=\frac{5 \mathrm{M}+30}{5} \\ \\ & \Rightarrow 2.9 \times 5 \times(6 \mathrm{M}+30)=2.8 \times 6 \times(5 \mathrm{M}+30) \\ \\ & \Rightarrow 87 \mathrm{M}+435=84 \mathrm{M}+504 \\ \\ & \Rightarrow 3 \mathrm{M}=69 \\ \\ & \Rightarrow \mathrm{M}=23 \mathrm{u} \end{aligned} $$

Therefore, the molar mass of the solute is $23 \mathrm{~g} \mathrm{~mol}^{-1}$.

(ii) Putting the value of ‘M’ in equation (i), we have:

$$ \begin{aligned} & \frac{p_{1}^{0}}{2.8}=\frac{5 \times 23+30}{5 \times 23} \\ \\ & \Rightarrow \frac{p_{1}^{0}}{2.8}=\frac{145}{115} \\ \\ & \Rightarrow p_{1}^{0}=3.53 \end{aligned} $$

Hence, the vapour pressure of water at $298 \mathrm{~K}$ is $3.53 \mathrm{kPa}$.

2.20 A $5 \%$ solution (by mass) of cane sugar in water has freezing point of $271 K$. Calculate the freezing point of $5 \%$ glucose in water if freezing point of pure water is $273.15 \mathrm{~K}$.

Answer

Here, $\Delta T_{f}=(273.15-271) \mathrm{K}$

$=2.15 \mathrm{~K}$

Molar mass of sugar $\left(\mathrm{C_12} \mathrm{H_22} \mathrm{O_11}\right)=12 \times 12+22 \times 1+11 \times 16$

$=342 \mathrm{~g} \mathrm{~mol}^{-1}$

$5 \%$ solution (by mass) of cane sugar in water means $5 \mathrm{~g}$ of cane sugar is present in $(100-5) \mathrm{g}=95 \mathrm{~g}$ of water.

Now, number of moles of cane sugar

$$ =\frac{5}{342} \mathrm{~mol} $$

$=0.0146 \mathrm{~mol}$

Therefore, molality of the solution,

$$ m=\frac{0.0146 \mathrm{~mol}}{0.095 \mathrm{~kg}} $$

$=0.1537 \mathrm{~mol} \mathrm{~kg}^{-1}$

Applying the relation,

$\Delta T_{f}=K_{f} \times m$

$ \begin{aligned} \Rightarrow K_{f} & =\frac{\Delta T_{f}}{m} \\ & =\frac{2.15 \mathrm{~K}}{0.1537 \mathrm{~mol} \mathrm{~kg}^{-1}} \end{aligned} $

$=13.99 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}$

Molar of glucose $\left(\mathrm{C_6} \mathrm{H_12} \mathrm{O_6}\right)=6 \times 12+12 \times 1+6 \times 16$

$=180 \mathrm{~g} \mathrm{~mol}^{-1}$

$5 \%$ glucose in water means $5 \mathrm{~g}$ of glucose is present in $(100-5) \mathrm{g}=95 \mathrm{~g}$ of water.

$\therefore$ Number of moles of glucose $=\frac{5}{180} \mathrm{~mol}$

$=0.0278 \mathrm{~mol}$

Therefore, molality of the solution,

$$ m=\frac{0.0278 \mathrm{~mol}}{0.095 \mathrm{~kg}} $$

$=0.2926 \mathrm{~mol} \mathrm{~kg}^{-1}$

Applying the relation,

$\Delta T_{f}=K_{f} \times m$

$=13.99 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1} \times 0.2926 \mathrm{~mol} \mathrm{~kg}^{-1}$

$=4.09 \mathrm{~K}$ (approximately)

Hence, the freezing point of $5 \%$ glucose solution is ($273.15$ - 4.09) K= $269.06 \mathrm{~K}$.

2.21 Two elements $A$ and $B$ form compounds having formula $A B_{2}$ and $A B_{4}$. When dissolved in $20 \mathrm{~g}$ of benzene $\left(\mathrm{C_6} \mathrm{H_6}\right), 1 \mathrm{~g}$ of $\mathrm{AB_2}$ lowers the freezing point by $2.3 \mathrm{~K}$ whereas $1.0 \mathrm{~g}$ of $\mathrm{AB_4}$ lowers it by $1.3 \mathrm{~K}$. The molar depression constant for benzene is $5.1 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}$. Calculate atomic masses of $\mathrm{A}$ and $\mathrm{B}$.

Answer

We know that, $M_{2}=\frac{1000 \times w_{2} \times k_{f}}{\Delta T_{f} \times w_{1}}$

Then, $M_{\mathrm{AB_2}}=\frac{1000 \times 1 \times 5.1}{2.3 \times 20}$

$=110.87 \mathrm{~g} \mathrm{~mol}^{-1}$

$M_{\mathrm{AB_4}}=\frac{1000 \times 1 \times 5.1}{1.3 \times 20}$

$=196.15 \mathrm{~g} \mathrm{~mol}^{-1}$

Now, we have the molar masses of $\mathrm{AB_2}$ and $\mathrm{AB_4}$ as $110.87 \mathrm{~g} \mathrm{~mol}^{-1}$ and $196.15 \mathrm{~g} \mathrm{~mol}^{-1}$ respectively.

Let the atomic masses of $A$ and $B$ be $x$ and $y$ respectively.

Now, we can write:

$x+2 y=110.87\quad \quad \quad \quad \text{(i)}$

$x+4 y=196.15\quad \quad \quad \quad \text{(ii)}$

Subtracting equation (i) from (ii), we have

$2 y=85.28$

$\Rightarrow y=42.64$

Putting the value of ’ $y$ ’ in equation (1), we have

$x+2 \times 42.64=110.87$

$\Rightarrow x=25.59$

Hence, the atomic masses of $A$ and $B$ are $25.59 \mathrm{u}$ and $42.64 \mathrm{u}$ respectively.

2.22 At $300 \mathrm{~K}, 36 \mathrm{~g}$ of glucose present in a litre of its solution has an osmotic pressure of 4.98 bar. If the osmotic pressure of the solution is 1.52 bars at the same temperature, what would be its concentration?

Answer

Here,

$T=300 \mathrm{~K}$

$\pi=1.52$ bar

$\mathrm{R}=0.083$ bar L K ${ }^{-1} \mathrm{~mol}^{-1}$

Applying the relation,

$\pi=C R T$

$ \begin{aligned} \Rightarrow C & =\frac{\pi}{\mathrm{R} T} \\ & =\frac{1.52 \mathrm{bar}}{0.083 \mathrm{bar} \mathrm{L} \mathrm{K}^{-1} \mathrm{~mol}^{-1} \times 300 \mathrm{~K}} \end{aligned} $

$=0.061 \mathrm{~mol}$

Since the volume of the solution is $1 \mathrm{~L}$, the concentration of the solution would be $0.061 \mathrm{M}$.

2.23 Suggest the most important type of intermolecular attractive interaction in the following pairs.

(i) n-hexane and n-octane

(ii) $\mathrm{I_2}$ and $\mathrm{CCl_4}$

(iii) $\mathrm{NaClO_4}$ and water

(iv) methanol and acetone

(v) acetonitrile $\left(\mathrm{CH_3} \mathrm{CN}\right)$ and acetone $\left(\mathrm{C_3} \mathrm{H_6} \mathrm{O}\right)$.

Answer

(i) Van der Wall’s forces of attraction.

(ii) Van der Wall’s forces of attraction.

(iii) Ion-diople interaction.

(iv) Dipole-dipole interaction.

(v) Dipole-dipole interaction.

2.24 Based on solute-solvent interactions, arrange the following in order of increasing solubility in n-octane and explain. Cyclohexane, $\mathrm{KCl}, \mathrm{CH_3} \mathrm{OH}, \mathrm{CH_3} \mathrm{CN}$.

Answer

$n$-octane is a non-polar solvent. Therefore, the solubility of a non-polar solute is more than that of a polar solute in the $n$-octane.

The order of increasing polarity is:

Cyclohexane $<\mathrm{CH_3} \mathrm{CN}<\mathrm{CH_3} \mathrm{OH}<\mathrm{KCl}$

Therefore, the order of increasing solubility is:

$\mathrm{KCl}<\mathrm{CH_3} \mathrm{OH}<\mathrm{CH_3} \mathrm{CN}<$ Cyclohexane

2.25 Amongst the following compounds, identify which are insoluble, partially soluble and highly soluble in water?

(i) phenol

(ii) toluene

(iii) formic acid

(iv) ethylene glycol

(v) chloroform

(vi) pentanol.

Answer

(i) Phenol $\left(\mathrm{C_6} \mathrm{H_5} \mathrm{OH}\right)$ has the polar group $-\mathrm{OH}$ and non-polar group $-\mathrm{C_6} \mathrm{H_5}$. Thus, phenol is partially soluble in water.

(ii) Toluene $\left(\mathrm{C_6} \mathrm{H_5}-\mathrm{CH_3}\right)$ has no polar groups. Thus, toluene is insoluble in water.

(iii) Formic acid $(\mathrm{HCOOH})$ has the polar group - $\mathrm{OH}$ and can form $\mathrm{H}$-bond with water. Thus, formic acid is highly soluble in water.

(iv) Ethylene glycol has polar - $\mathrm{OH}$ group and can form $\mathrm{H}$-bond. Thus, it is highly soluble in water.

(v) Chloroform is insoluble in water.

(vi) Pentanol $\left(\mathrm{C_5} \mathrm{H_11} \mathrm{OH}\right)$ has polar $-\mathrm{OH}$ group, but it also contains a very bulky non-polar $-\mathrm{C_5} \mathrm{H_11}$ group. Thus, pentanol is partially soluble in water.

2.26 If the density of some lake water is $1.25 \mathrm{~g} \mathrm{~mL}^{-1}$ and contains $92 \mathrm{~g}$ of $\mathrm{Na}^{+}$ ions per $\mathrm{kg}$ of water, calculate the molarity of $\mathrm{Na}^{+}$ ions in the lake.

Answer

Number of moles present in $92 \mathrm{~g}$ of $\mathrm{Na}^{+}$ions $=\frac{92 \mathrm{~g}}{23 \mathrm{~g} \mathrm{~mol}^{-1}}$

$=4 \mathrm{~mol}$

Therefore, molality of $\mathrm{Na}^{+}$ions in the lake $=\frac{4 \mathrm{~mol}}{1 \mathrm{~kg}}$

$=4 \mathrm{~m}$

2.27 If the solubility product of CuS is $6 \times 10^{-16}$, calculate the maximum molarity of CuS in aqueous solution.

Answer

Solubility product of CuS, $K_{\mathrm{sp}}=6 \times 10^{-16}$

Let $s$ be the solubility of CuS in $\mathrm{mol}^{-1}$.

$\mathrm{CuS} \leftrightarrow \mathrm{Cu}^{2+}+\mathrm{S}^{2-}$

Now, $K_{s p}=\left[\mathrm{Cu}^{2+}\right]\left[\mathrm{S}^{2-}\right]$

$=s \times s$

$=s^{2}$

Then, we have, $K_{\mathrm{sp}}=s^{2}=6 \times 10^{-16}$

$\Rightarrow s=\sqrt{6 \times 10^{-16}}$

$=2.45 \times 10^{-8} \mathrm{~mol} \mathrm{~L}^{-1}$

Hence, the maximum molarity of CuS in an aqueous solution is $2.45 \times 10^{-8} \mathrm{~mol} \mathrm{~L}^{-1}$.

2.28 Calculate the mass percentage of aspirin $\left(\mathrm{C_9} \mathrm{H_8} \mathrm{O_4}\right)$ in acetonitrile $\left(\mathrm{CH_3} \mathrm{CN}\right)$ when $6.5 \mathrm{~g}$ of $\mathrm{C_9} \mathrm{H_8} \mathrm{O_4}$ is dissolved in $450 \mathrm{~g}$ of $\mathrm{CH_3} \mathrm{CN}$.

Answer

$6.5 \mathrm{~g}$ of $\mathrm{C_9} \mathrm{H_8} \mathrm{O_4}$ is dissolved in $450 \mathrm{~g}$ of $\mathrm{CH_3} \mathrm{CN}$.

Then, total mass of the solution $=(6.5+450) \mathrm{g}$

$=456.5 \mathrm{~g}$

Therefore, mass percentage of $\mathrm{C_9} \mathrm{H_8} \mathrm{O_4}$

$$ =\frac{6.5}{456.5} \times 100 \% $$

$=1.424 \%$

2.29 Nalorphene $\left(\mathrm{C_19} \mathrm{H_21} \mathrm{NO_3}\right)$, similar to morphine, is used to combat withdrawal symptoms in narcotic users. Dose of nalorphene generally given is $1.5 \mathrm{mg}$. Calculate the mass of $1.5 \times 10^{-3} \mathrm{~m}$ aqueous solution required for the above dose.

Answer

The molar mass of nalorphene $\left(\mathrm{C_19} \mathrm{H_21} \mathrm{NO_3}\right)$ is given as:

$19 \times 12+21 \times 1+1 \times 14+3 \times 16=311 \mathrm{~g} \mathrm{~mol}^{-1}$

In $1.5 \times 10^{-3} \mathrm{~m}$ aqueous solution of nalorphene,

$1 \mathrm{~kg}(1000 \mathrm{~g})$ of water contains $1.5 \times 10^{-3} \mathrm{~mol}=1.5 \times 10^{-3} \times 311 \mathrm{~g}$

$=0.4665 \mathrm{~g}$

Therefore, total mass of the solution $=(1000+0.4665) \mathrm{g}$

$=1000.4665 \mathrm{~g}$

This implies that the mass of the solution containing $0.4665 \mathrm{~g}$ of nalorphene is $1000.4665 \mathrm{~g}$.

Therefore, mass of the solution containing $1.5 \mathrm{mg}$ of nalorphene is:

$$ \begin{aligned} & \frac{1000.4665 \times 1.5 \times 10^{-3}}{0.4665} \mathrm{~g} \\ & =3.22 \mathrm{~g} \end{aligned} $$

Hence, the mass of aqueous solution required is $3.22 \mathrm{~g}$.

Note:There is a slight variation in this answer and the one given in the NCERT textbook.

2.30 Calculate the amount of benzoic acid $\left(\mathrm{C_6} \mathrm{H_5} \mathrm{COOH}\right)$ required for preparing 250 $\mathrm{mL}$ of $0.15 \mathrm{M}$ solution in methanol.

Answer

$0.15 \mathrm{M}$ solution of benzoic acid in methanol means,

$1000 \mathrm{~mL}$ of solution contains $0.15 \mathrm{~mol}$ of benzoic acid

Therefore, $250 \mathrm{~mL}$ of solution contains $=\frac{0.15 \times 250}{1000}$ mol of benzoic acid

$=0.0375 \mathrm{~mol}$ of benzoic acid

Molar mass of benzoic acid $\left(\mathrm{C_6} \mathrm{H_5} \mathrm{COOH}\right)=7 \times 12+6 \times 1+2 \times 16$

$=122 \mathrm{~g} \mathrm{~mol}^{-1}$

Hence, required benzoic acid $=0.0375 \mathrm{~mol} \times 122 \mathrm{~g} \mathrm{~mol}^{-1}$

$=4.575 \mathrm{~g}$

2.31 The depression in freezing point of water observed for the same amount of acetic acid, trichloroacetic acid and trifluoroacetic acid increases in the order given above. Explain briefly.

Answer

Among $\mathrm{H}, \mathrm{Cl}$, and $\mathrm{F}, \mathrm{H}$ is least electronegative while $\mathrm{F}$ is most electronegative. Then, $\mathrm{F}$ can withdraw electrons towards itself more than $\mathrm{Cl}$ and $\mathrm{H}$. Thus, trifluoroacetic acid can easily lose $\mathrm{H}^{+}$ions i.e., trifluoroacetic acid ionizes to the largest extent. Now, the more ions produced, the greater is the depression of the freezing point. Hence, the depression in the freezing point increases in the order:

Acetic acid < trichloroacetic acid < trifluoroacetic acid

2.32 Calculate the depression in the freezing point of water when $10 \mathrm{~g}$ of $\mathrm{CH_3} \mathrm{CH_2} \mathrm{CHClCOOH}$ is added to $250 \mathrm{~g}$ of water. $\mathrm{K_\mathrm{a}}=1.4 \times 10^{-3}, K_{\mathrm{f}}=1.86$

Answer

Molar mass of $\mathrm{CH_3} \mathrm{CH_2} \mathrm{CHClCOOH}=15+14+13+35.5+12+16+16+1$

$=122.5 \mathrm{~g} \mathrm{~mol}^{-1}$

$\therefore$ No. of moles present in $10 \mathrm{~g}$ of

$$ \mathrm{CH_3} \mathrm{CH_2} \mathrm{CHClCOOH}=\frac{10 \mathrm{~g}}{122.5 \mathrm{~g} \mathrm{~mol}^{-1}} $$

$=0.0816 \mathrm{~mol}$

It is given that $10 \mathrm{~g}$ of

$\mathrm{CH_3} \mathrm{CH_2} \mathrm{CHClCOOH}$ is added to $250 \mathrm{~g}$ of water.

$\therefore$ Molality of the solution,

$$ =\frac{0.0186}{250} \times 1000 $$

$=0.3264 \mathrm{~mol} \mathrm{~kg}^{-1}$

Let $a$ be the degree of dissociation of $\mathrm{CH_3} \mathrm{CH_2} \mathrm{CHClCOOH}$.

$\mathrm{CH_3} \mathrm{CH_2} \mathrm{CHClCOOH}$ undergoes dissociation according to the following equation:

$ \begin{array}{lcccc} & \mathrm{CH_3} \mathrm{CH_2} \mathrm{CHClCOOH} &\leftrightarrow &\mathrm{CH_3} \mathrm{CH_2} \mathrm{CHClCOO}^{-}& +\mathrm{H}^{+} \\ \text{Initial conc. } & \mathrm{C} \text{mol L}^{-1} & & 0 & 0 \\ \text{At equilibrium } & \mathrm{C1-\alpha} & & \mathrm{C\alpha} & \mathrm{C\alpha} \end{array} $

$ \begin{aligned} & \therefore K_{a}=\frac{C \alpha \cdot C \alpha}{C(1-\alpha)} \\ & =\frac{C \alpha^{2}}{1-\alpha} \end{aligned} $

Since $\alpha$ is very small with respect to $1,1-\alpha$

Now,

$ K_{a}=\frac{C \alpha^{2}}{1} $

$\Rightarrow K_{a}=C \alpha^{2}$

$\Rightarrow \alpha=\sqrt{\frac{K_{a}}{C}}$

$$ \begin{aligned} & =\sqrt{\frac{1.4 \times 10^{-3}}{0.3264}} \quad\left(\because K_{a}=1.4 \times 10^{-3}\right) \\ & =0.0655 \end{aligned} $$

Again,

$ \begin{array}{lcccc} & \mathrm{CH_3} \mathrm{CH_2} \mathrm{CHClCOOH} &\leftrightarrow &\mathrm{CH_3} \mathrm{CH_2} \mathrm{CHClCOO}^{-}& +\mathrm{H}^{+} \\ \text{Initial conc. } & 1 & & 0 & 0 \\ \text{At equilibrium } & \mathrm{1-\alpha} & & \mathrm{\alpha} & \mathrm{\alpha} \end{array} $

Initial moles	1	0	0
At equilibrium	$1-\alpha$	$\alpha$	$\alpha$

Total moles of equilibrium $=1-\alpha+\alpha+\alpha$

$$ \begin{aligned} & =1+\alpha \\ & \therefore i=\frac{1+\alpha}{1} \\ & =1+\alpha \\ & =1+0.0655 \\ & =1.0655 \end{aligned} $$

Hence, the depression in the freezing point of water is given as:

$$ \begin{aligned} & \Delta T_{f}=i . K_{f} m \\ & =1.0655 \times 1.86 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1} \times 0.3264 \mathrm{~mol} \mathrm{~kg}^{-1} \\ & =0.65 \mathrm{~K} \end{aligned} $$

2.33 $19 .5 \mathrm{~g}$ of $\mathrm{CH_2} \mathrm{FCOOH}$ is dissolved in $500 \mathrm{~g}$ of water. The depression in the freezing point of water observed is $1.0^{\circ} \mathrm{C}$. Calculate the van’t Hoff factor and dissociation constant of fluoroacetic acid.

Answer

It is given that:

$w_{1}=500 \mathrm{~g}$

$w_{2}=19.5 \mathrm{~g}$

$K_{f}=1.86 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}$

$\Delta T_{f}=1 \mathrm{~K}$

We know that:

$M_{2}=\frac{K_{f} \times w_{2} \times 1000}{\Delta T_{f} \times w_{1}}$

$=\frac{1.86 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1} \times 19.5 \mathrm{~g} \times 1000 \mathrm{~g} \mathrm{~kg}^{-1}}{500 \mathrm{~g} \times 1 \mathrm{~K}}$

$=72.54 \mathrm{~g} \mathrm{~mol}^{-1}$

Therefore, observed molar mass of $\mathrm{CH_2} \mathrm{FCOOH},\left(M_{2}\right)_{\text {obs }}=72.54 \mathrm{~g} \mathrm{~mol}$

The calculated molar mass of $\mathrm{CH_2} \mathrm{FCOOH_\text {is: }}$

$\left(M_{2}\right)_{\text {cal }}=14+19+12+16+16+1$

$=78 \mathrm{~g} \mathrm{~mol}^{-1}$

$=\frac{78 \mathrm{~g} \mathrm{~mol}^{-1}}{72.54 \mathrm{~g} \mathrm{~mol}^{-1}}$

$=1.0753$

Let abe the degree of dissociation of $\mathrm{CH_2} \mathrm{FCOOH}$

$ \begin{array}{lcccc} & \mathrm{CH_2} \mathrm{FCOOH} &\leftrightarrow &\mathrm{CH_2} \mathrm{FCOO}^{-}& +\mathrm{H}^{+} \\ \text{Initial conc. } & \mathrm{C} \text{mol L}^{-1} & & 0 & 0 \\ \text{At equilibrium } & \mathrm{C1-\alpha} & & \mathrm{C\alpha} & \mathrm{C\alpha} \end{array} $

$\text { Total }=\mathrm{C}(1+\alpha)$

$$ \begin{aligned} & \therefore i=\frac{C(1+\alpha)}{C} \\ \\ & \Rightarrow i=1+\alpha \\ \\ & \Rightarrow \alpha=i-1 \\ \\ & =1.0753-1 \\ \\ & =0.0753 \end{aligned} $$

Now, the value of $K_{a}$ is given as:

$$ \begin{aligned} K_{a} & =\frac{\left[\mathrm{CH_2} \mathrm{FCOO}^{-}\right]\left[\mathrm{H}^{+}\right]}{\left[\mathrm{CH_2} \mathrm{FCOOH}\right]} \\ \\ = & \frac{C \alpha \cdot C \alpha}{C(1-\alpha)} \\ \\ = & \frac{C \alpha^{2}}{1-\alpha} \end{aligned} $$

Taking the volume of the solution as $500 \mathrm{~mL}$, we have the concentration:

$$ \begin{aligned} & C=\frac{\frac{19.5}{78}}{500} \times 1000 \mathrm{M} \\ \\ & =0.5 \mathrm{M} \\ \\ & \qquad K_{a}=\frac{C \alpha^{2}}{1-\alpha} \\ \\ & \text { Therefore, } \\ \\ & =\frac{0.5 \times(0.0753)^{2}}{1-0.0753} \\ \\ & =\frac{0.5 \times 0.00567}{0.9247} \\ \\ & =0.00307 \text { (approximately) } \\ \\ & =3.07 \times 10^{-3} \end{aligned} $$

2.34 Vapour pressure of water at $293 \mathrm{~K}$ is $17.535 \mathrm{~mm}$ Hg. Calculate the vapour pressure of water at $293 \mathrm{~K}$ when $25 \mathrm{~g}$ of glucose is dissolved in $450 \mathrm{~g}$ of water.

Answer

Vapour pressure of water, $p_{1}^{0}=17.535 \mathrm{~mm}$ of $\mathrm{Hg}$

Mass of glucose, $w_{2}=25 \mathrm{~g}$

Mass of water, $w_{1}=450 \mathrm{~g}$

We know that,

Molar mass of glucose $\left(\mathrm{C_6} \mathrm{H_12} \mathrm{O_6}\right), M_{2}=6 \times 12+12 \times 1+6 \times 16$

$=180 \mathrm{~g} \mathrm{~mol}^{-1}$

Molar mass of water, $M_{1}=18 \mathrm{~g} \mathrm{~mol}^{-1}$

Then, number of moles of glucose, $\quad n_{2}=\frac{25}{180 \mathrm{~g} \mathrm{~mol}^{-1}}$

$=0.139 \mathrm{~mol}$

And, number of moles of water,

$$ n_{1}=\frac{450 \mathrm{~g}}{18 \mathrm{~g} \mathrm{~mol}^{-1}} $$

$=25 \mathrm{~mol}$

We know that,

$\frac{p_{1}^{0}-p_{1}}{p_{1}^{0}}=\frac{n_{1}}{n_{2}+n_{1}}$

$\Rightarrow \frac{17.535-p_{1}}{17.535}=\frac{0.139}{0.139+25}$

$\Rightarrow 17.535-p_{1}=\frac{0.139 \times 17.535}{25.139}$

$\Rightarrow 17.535-p_{1}=0.097$

$\Rightarrow p_{1}=17.44 \mathrm{~mm}$ of $\mathrm{Hg}$

Hence, the vapour pressure of water is $17.44 \mathrm{~mm}$ of $\mathrm{Hg}$.

2.35 Henry’s law constant for the molality of methane in benzene at $298 \mathrm{~K}$ is $4.27 \times 10^{5} \mathrm{~mm} \mathrm{Hg}$. Calculate the solubility of methane in benzene at $298 \mathrm{~K}$ under $760 \mathrm{~mm} \mathrm{Hg}$.

Answer

Here,

$p=760 \mathrm{~mm} \mathrm{Hg}$

$\mathrm{k_\mathrm{H}}=4.27 \times 10^{5} \mathrm{~mm} \mathrm{Hg}$

According to Henry’s law,

$p=\mathrm{k_\mathrm{H}} \mathrm{X}$

$\Rightarrow x=\frac{p}{k_{\mathrm{H}}}$

$ =\frac{760 \mathrm{~mm} \mathrm{Hg}}{4.27 \times 10^{5} \mathrm{~mm} \mathrm{Hg}} $

$=177.99 \times 10^{-5}$

$=178 \times 10^{-5}$ (approximately)

Hence, the mole fraction of methane in benzene is $178 \times 10^{-5}$.

2.36 $100 \mathrm{~g}$ of liquid A (molar mass $140 \mathrm{~g} \mathrm{~mol}^{-1}$ ) was dissolved in $1000 \mathrm{~g}$ of liquid $\mathrm{B}$ (molar mass $180 \mathrm{~g} \mathrm{~mol}^{-1}$ ). The vapour pressure of pure liquid $\mathrm{B}$ was found to be 500 torr. Calculate the vapour pressure of pure liquid $A$ and its vapour pressure in the solution if the total vapour pressure of the solution is 475 Torr.

Answer

Number of moles of liquid A, $\quad n_{\mathrm{A}}=\frac{100}{140} \mathrm{~mol}$

$=0.714 \mathrm{~mol}$

Number of moles of liquid $B$,

$$ n_{\mathrm{B}}=\frac{1000}{180} \mathrm{~mol} $$

$=5.556 \mathrm{~mol}$

Then, mole fraction of $\mathrm{A}$,

$$ x_{\mathrm{A}}=\frac{n_{\mathrm{A}}}{n_{\mathrm{A}}+n_{\mathrm{B}}} $$

$=\frac{0.714}{0.714+5.556}$

$=0.114$

And, mole fraction of $\mathrm{B}, x_{\mathrm{B}}=1-0.114$

$=0.886$

Vapour pressure of pure liquid $\mathrm{B}, p_{\mathrm{B}}^{0}=500$ torr

Therefore, vapour pressure of liquid $B$ in the solution,

$$ p_{\mathrm{B}}=p_{\mathrm{B}}^{0} x_{\mathrm{B}} $$

$=500 \times 0.886$ $=443$ torr

Total vapour pressure of the solution, $p_{\text {total }}=475$ torr

$\therefore$ Vapour pressure of liquid $\mathrm{A}$ in the solution,

$p_{\mathrm{A}}=p_{\text {total }}-p_{\mathrm{B}}$

$=475-443$

$=32$ torr

Now,

$ \begin{aligned} p_{\mathrm{A}} & =p_{\mathrm{A}}^{0} x_{\mathrm{A}} \\ \\ \Rightarrow p_{\mathrm{A}}^{0} & =\frac{p_{\mathrm{A}}}{x_{\mathrm{A}}} \\ \\ & =\frac{32}{0.114} \end{aligned} $

$=280.7$ torr

Hence, the vapour pressure of pure liquid A is 280.7 torr.

2.37 Vapour pressures of pure acetone and chloroform at $328 \mathrm{~K}$ are $741.8 \mathrm{~mm}$ $\mathrm{Hg}$ and $632.8 \mathrm{~mm} \mathrm{Hg}$ respectively. Assuming that they form ideal solution over the entire range of composition, plot $p_{\text {total }}, p_{\text {chloroform }}$, and $p_{\text {acetone }}$ as a function of $x_{\text {acetone }}$. The experimental data observed for different compositions of mixture is:

$100 \times x_{\text {acetone }}$	0	11.8	23.4	36.0	50.8	58.2	64.5	72.1
$\mathrm{p_\text {acetone }} / \mathrm{mm} \mathrm{Hg}$	0	54.9	110.1	202.4	322.7	405.9	454.1	521.1
$\mathrm{p_\text {chloroform }} / \mathrm{mm} \mathrm{Hg}$	632.8	548.1	469.4	359.7	257.7	193.6	161.2	120.7

Plot this data also on the same graph paper. Indicate whether it has positive deviation or negative deviation from the ideal solution.

Answer

From the question, we have the following data

$\mathbf{1 0 0} \times \boldsymbol{X_\text {actone }}$	0	11.8	23.4	36.0	50.8	58.2	64.5	72.1
$\mathbf{p_\text {acetone }} / \mathbf{m m} \mathbf{H g}$	0	54.9	110.1	202.4	322.7	405.9	454.1	521.1
$\mathbf{p_\text {chloroform }} / \mathbf{m m} \mathbf{H g}$	632.8	548.1	469.4	359.7	257.7	193.6	161.2	120.7
$\mathbf{p_\text {tota }}(\mathbf{m m} \mathbf{H g})$	632.8	603.0	579.5	562.1	580.4	599.5	615.3	641.8

It can be observed from the graph that the plot for the $p_{\text {total }}$ of the solution curves downwards. Therefore, the solution shows negative deviation from the ideal behaviour.

2.38 Benzene and toluene form ideal solution over the entire range of composition. The vapour pressure of pure benzene and toluene at $300 \mathrm{~K}$ are $50.71 \mathrm{~mm} \mathrm{Hg}$ and $32.06 \mathrm{~mm} \mathrm{Hg}$ respectively. Calculate the mole fraction of benzene in vapour phase if $80 \mathrm{~g}$ of benzene is mixed with $100 \mathrm{~g}$ of toluene.

Answer

Molar mass of benzene $\left(\mathrm{C_6} \mathrm{H_6}\right)=6 \times 12+6 \times 1$

$=78 \mathrm{~g} \mathrm{~mol}^{-1}$

Molar mass of toluene $\left(\mathrm{C_6} \mathrm{H_5} \mathrm{CH_3}\right)=7 \times 12+8 \times 1$

$=92 \mathrm{~g} \mathrm{~mol}^{-1}$

Now, no. of moles present in $80 \mathrm{~g}$ of benzene $=\frac{80}{78} \mathrm{~mol}=1.026 \mathrm{~mol}$

And, no. of moles present in $100 \mathrm{~g}$ of toluene $=\frac{100}{92} \mathrm{~mol}=1.087 \mathrm{~mol}$

$\therefore$ Mole fraction of benzene, $x_{b}=\frac{1.026}{1.026+1.087}=0.486$

And, mole fraction of toluene, $x_{t}=1-0.486=0.514$

It is given that vapour pressure of pure benzene, $p_{b}^{0}=50.71 \mathrm{~mm} \mathrm{Hg}$

And, vapour pressure of pure toluene, $p_{t}^{0}=32.06 \mathrm{~mm} \mathrm{Hg}$

Therefore, partial vapour pressure of benzene, $p_{b}=x_{b} \times p_{b}$

$=0.486 \times 50.71$

$=24.645 \mathrm{~mm} \mathrm{Hg}$

And, partial vapour pressure of toluene, $p_{t}=x_{t} \times p_{t}$

$=0.514 \times 32.06$

$=16.479 \mathrm{~mm} \mathrm{Hg}$

Hence, mole fraction of benzene in vapour phase is given by:

$ \begin{aligned} & \frac{p_{b}}{p_{b}+p_{t}} \\ & =\frac{24.645}{24.645+16.479} \\ & =\frac{24.645}{41.124} \\ & =0.599 \\ & =0.6 \end{aligned} $

2.39 The air is a mixture of a number of gases. The major components are oxygen and nitrogen with approximate proportion of $20 \%$ is to $79 \%$ by volume at 298 $K$. The water is in equilibrium with air at a pressure of $10 \mathrm{~atm}$. At $298 \mathrm{~K}$ if the Henry’s law constants for oxygen and nitrogen at $298 \mathrm{~K}$ are $3.30 \times 10^{7} \mathrm{~mm}$ and $6.51 \times 10^{7} \mathrm{~mm}$ respectively, calculate the composition of these gases in water.

Answer

Percentage of oxygen $\left(\mathrm{O_2}\right)$ in air $=20 \%$

Percentage of nitrogen $\left(\mathrm{N_2}\right)$ in air $=79 \%$

Also, it is given that water is in equilibrium with air at a total pressure of $10 \mathrm{~atm}$, that is, $(10 \times 760) \mathrm{mm} \mathrm{Hg}=7600 \mathrm{~mm}$ $\mathrm{Hg}$

Therefore,

Partial pressure of oxygen, $p_{\mathrm{O_2}}=\frac{20}{100} \times 7600 \mathrm{~mm} \mathrm{Hg}$

$=1520 \mathrm{~mm} \mathrm{Hg}$

Partial pressure of nitrogen,

$$ p_{\mathrm{N_2}}=\frac{79}{100} \times 7600 \mathrm{mmHg} $$

$=6004 \mathrm{mmHg}$

Now, according to Henry’s law:

$p=K_{\mathrm{H}} \cdot X$

For oxygen:

$$ \begin{aligned} p_{\mathrm{O_2}}= & K_{\mathrm{H}} \cdot x_{\mathrm{O_2}} \\ \Rightarrow x_{\mathrm{O_2}} & =\frac{p_{\mathrm{O_2}}}{K_{\mathrm{H}}} \\ & \left.=\frac{1520 \mathrm{~mm} \mathrm{Hg}}{3.30 \times 10^{7} \mathrm{~mm} \mathrm{Hg}} \quad \text { (Given } K_{\mathrm{H}}=3.30 \times 10^{7} \mathrm{~mm} \mathrm{Hg}\right) \\ & =4.61 \times 10^{-5} \end{aligned} $$

For nitrogen:

$$ \begin{aligned} p_{\mathrm{N_2}}= & K_{\mathrm{H}} \cdot x_{\mathrm{N_2}} \\ \Rightarrow x_{\mathrm{N_2}} & =\frac{p_{\mathrm{N_2}}}{K_{\mathrm{H}}} \\ & =\frac{6004 \mathrm{~mm} \mathrm{Hg}}{6.51 \times 10^{7} \mathrm{~mm} \mathrm{Hg}} \\ & =9.22 \times 10^{-5} \end{aligned} $$

Hence, the mole fractions of oxygen and nitrogen in water are $4.61 \times 10^{-5}$ and $9.22 \times 10^{-5}$ respectively.

2.40 Determine the amount of $\mathrm{CaCl_2}(i=2.47)$ dissolved in 2.5 litre of water such that its osmotic pressure is $0.75 \mathrm{~atm}$ at $27^{\circ} \mathrm{C}$.

Answer

We know that,

$\pi=i \frac{n}{V} \mathrm{R} T$

$\Rightarrow \pi=i \frac{w}{M V} \mathrm{R} T$

$\Rightarrow w=\frac{\pi M V}{i \mathrm{R} T}$ $\pi=0.75 \mathrm{~atm}$

$V=2.5 \mathrm{~L}$

$i=2.47$

$T=(27+273) \mathrm{K}=300 \mathrm{~K}$

Here,

$\mathrm{R}=0.0821 \mathrm{~L} \mathrm{~atm} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}$

$M=1 \times 40+2 \times 35.5$

$=111 \mathrm{~g} \mathrm{~mol}^{-1}$

Therefore, $w=\frac{0.75 \times 111 \times 2.5}{2.47 \times 0.0821 \times 300}$

$=3.42 \mathrm{~g}$

Hence, the required amount of $\mathrm{CaCl_2}$ is $3.42 \mathrm{~g}$.

2.41 Determine the osmotic pressure of a solution prepared by dissolving $25 \mathrm{mg}$ of $\mathrm{K_2} \mathrm{SO_4}$ in 2 litre of water at $25^{\circ} \mathrm{C}$, assuming that it is completely dissociated.

Answer

When $\mathrm{K_2} \mathrm{SO_4}$ is dissolved in water, $\mathrm{K}^{+}$and $\mathrm{SO_4}^{2-}$ ions are produced.

$\mathrm{K_2} \mathrm{SO_4} \longrightarrow 2 \mathrm{~K}^{+}+\mathrm{SO_4}^{2-}$

Total number of ions produced $=3$

$\therefore i=3$

Given,

$w=25 \mathrm{mg}=0.025 \mathrm{~g}$

$V=2 \mathrm{~L}$

$T=25^{\circ} \mathrm{C}=(25+273) \mathrm{K}=298 \mathrm{~K}$

Also, we know that:

$\mathrm{R}=0.0821 \mathrm{~L} \mathrm{~atm} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}$

$M=(2 \times 39)+(1 \times 32)+(4 \times 16)=174 \mathrm{~g} \mathrm{~mol}^{-1}$

Appling the following relation,

$ \begin{aligned} \pi & =i \frac{n}{v} \mathrm{R} T \\ & =i \frac{w}{M} \frac{1}{v} \mathrm{R} T \\ & =3 \times \frac{0.025}{174} \times \frac{1}{2} \times 0.0821 \times 298 \\ & =5.27 \times 10^{-3} \mathrm{~atm} \end{aligned} $