Sine Rule:

$\quad \quad \quad \quad \frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$

Cosine Formula:

• $ \cos A=\frac{b^{2}+c^{2}-a^{2}}{2 b c}$

• $ \cos B=\frac{c^{2}+a^{2}-b^{2}}{2 c a} $

• $ \cos C=\frac{a^{2}+b^{2}-c^{2}}{2 a b}$

Projection Formula:

• $ a=b \cos C+c \cos B$

• $ b=c \cos A+a \cos C$

• $ c=a \cos B+b \cos A$

Napier’s Analogy (Tangent Rule):

• $ \tan \frac{\mathrm{B}-\mathrm{C}}{2}=\frac{\mathrm{b}-\mathrm{c}}{\mathrm{b}+\mathrm{c}} \cot \frac{\mathrm{A}}{2}$

• $ \tan \frac{C-A}{2}=\frac{c-a}{c+a} \cot \frac{B}{2}$

• $ \tan \frac{A-B}{2}=\frac{a-b}{a+b} \cot \frac{C}{2}$

Trigonometric Functions of Half Angles:

• $ \sin \frac{\Lambda}{2}=\sqrt{\frac{(\mathrm{s}-\mathrm{b})(\mathrm{s}-\mathrm{c})}{\mathrm{bc}}} $

• $ \sin \frac{\mathrm{B}}{2}=\sqrt{\frac{(\mathrm{s}-\mathrm{c})(\mathrm{s}-\mathrm{a})}{\mathrm{ca}}}$

• $ \sin \frac{\mathrm{C}}{2}=\sqrt{\frac{(\mathrm{s}-\mathrm{a})(\mathrm{s}-\mathrm{b})}{\mathrm{ab}}}$

• $ \cos \frac{\mathrm{A}}{2}=\sqrt{\frac{\mathrm{s}(\mathrm{s}-\mathrm{a})}{\mathrm{bc}}} $

• $ \cos \frac{\mathrm{B}}{2}=\sqrt{\frac{\mathrm{s}(\mathrm{s}-\mathrm{b})}{\mathrm{ca}}}$

• $ \cos \frac{\mathrm{C}}{2}=\sqrt{\frac{\mathrm{s}(\mathrm{s}-\mathrm{c})}{\mathrm{ab}}}$

• $ \tan \frac{\Lambda}{2}=\sqrt{\frac{(\mathrm{s}-\mathrm{b})(\mathrm{s}-\mathrm{c})}{\mathrm{s}(\mathrm{s}-\mathrm{a})}}=\frac{\Delta}{\mathrm{s}(\mathrm{s}-\mathrm{a})}$

  where, $\mathrm{s}=\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{2}\hspace{1mm} \text{ is semi perimetre of triangle.}$

• $ \sin A=\frac{2}{b c} \sqrt{s(s-a)(s-b)(s-c)}=\frac{2 \Delta}{b c}$

Area of Triangle $(\Delta)$:

$$\quad \Delta=\frac{1}{2} a b \sin C=\frac{1}{2} b c \sin A=\frac{1}{2} c a \sin B=\sqrt{s(s-a)(s-b)(s-c)}$$

$\mathbf{m}$-n Rule:

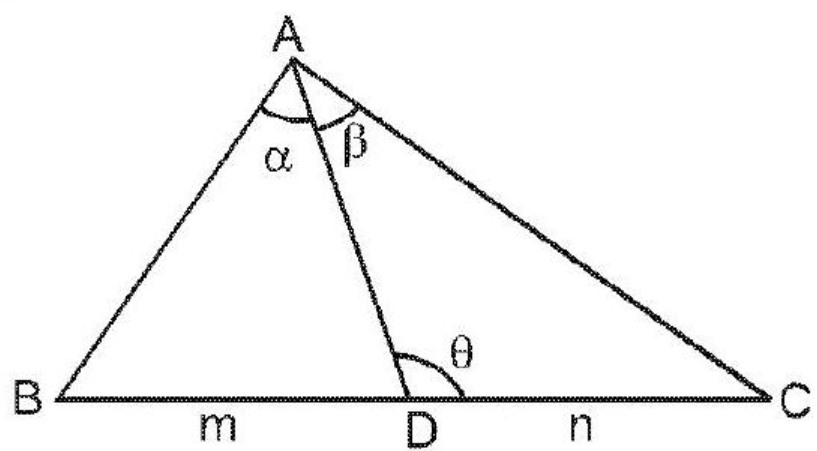
$\quad \ \text{If} \ B D: D C=m: n, then$

$$ \begin{aligned} (m+n) \cot \theta & =m \cot \alpha-n \cot \beta \ & =n \cot B-m \cot C \end{aligned} $$

Radius of Circumcirlce :

$$ R=\frac{a}{2 \sin A}=\frac{b}{2 \sin B}=\frac{c}{2 \sin C}=\frac{a b c}{4 \Delta} $$

Radius of The Incircle :

• $ r=\frac{\Delta}{s}$

• $ r=(s-a) \tan \frac{A}{2}=(s-b) \tan \frac{B}{2}=(s-c) \tan \frac{C}{2}$

• $ r=\frac{a \sin \frac{B}{2} \sin \frac{C}{2}}{\cos \frac{A}{2}}\hspace{1mm} $

• $ r=4 R \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2}$

Radius of The Ex-Circles :

• $ r_{1}=\frac{\Delta}{s-a} ; r_{2}=\frac{\Delta}{s-b} ; r_{3}=\frac{\Delta}{s-c}$

• $ r_{1}=s \tan \frac{A}{2} ; r_{2}=s \tan \frac{B}{2} ; r_{3}=s \tan \frac{\mathrm{C}}{2}$

• $ r_{1}=\frac{a \cos \frac{B}{2} \cos \frac{C}{2}}{\cos \frac{A}{2}}\hspace{1mm}$

• $ r_{1}=4 R \sin \frac{A}{2} \cdot \cos \frac{B}{2} \cdot \cos \frac{C}{2}$

Length of Angle Bisectors, Medians & Altitudes :

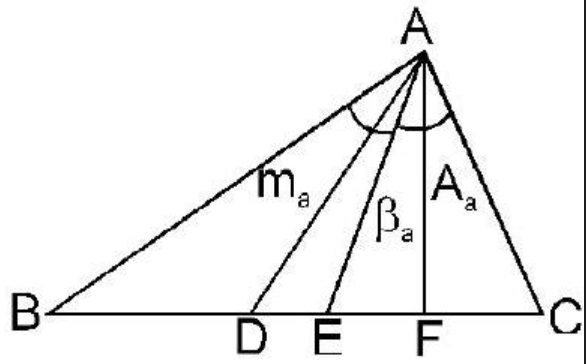
• Length of an angle bisector from the angle $A=\beta_{a}=\frac{2 b c \cos \frac{A}{2}}{b+c}$

• Length of median from the angle $A=m_{a}=\frac{1}{2} \sqrt{2 b^{2}+2 c^{2}-a^{2}}$

• Length of altitude from the angle $A=A_{a}=\frac{2 \Delta}{a}$

The Distances of The Special Points from Vertices and Sides of Triangle:

PYQ-2023-Straight-Line-Q9, PYQ-2023-Parabola-Q1

• Circumcentre (O)

$$ O A=R \ \text{and} \ O_{a}=R \cos A $$

• Incentre (I)

$$ I A= r \operatorname{cosec} \frac{A}{2} \text{and} \ I_{a}=r $$

• Excentre $ \left(I_{1}\right)$

$$ I_{1} A=r_{1} \operatorname{cosec} \frac{A}{2}$$

• Orthocentre

$$ H A=2 R \cos A \ \text{and} \ H_{a}=2 R \cos B \cos C$$

• Centroid (G)

$$ GA =\frac{1}{3} \sqrt{2 b^{2}+2 c^{2}-a^{2}} \ \text{and} \ G_{a}=\frac{2 \Delta}{3 a}$$

Orthocentre and Pedal Triangle:

$ \quad $ The triangle KLM which is formed by joining the feet of the altitudes is called the Pedal Triangle.

• Its angles are $\pi-2 A, \pi-2 B$ and $\pi-2 C$.

• Its sides are a $\cos A=R \sin 2 A$,$b \cos B=R \sin 2 B \hspace{1mm} \text { and } \hspace{1mm} c \cos C=R \sin 2 C$

• Circumradii of the triangles $\mathrm{PBC}, \mathrm{PCA}, \mathrm{PAB}$ and $\mathrm{ABC}$ are equal.

Excentral Triangle:

• The triangle formed by joining the three excentres $I_{1}, I_{2}$ and $I_{3}$ of $\triangle A B C$ is called the excentral or excentric triangle.

• $ \triangle ABC$ is the pedal triangle of the $\Delta I_1 I_2 I_3$.

• Its angles are $\frac{\pi}{2}-\frac{A}{2}, \frac{\pi}{2}-\frac{B}{2} \hspace{1mm}$ & $\hspace{1mm}\frac{\pi}{2}-\frac{C}{2}$.

• Its sides are $4 R \cos \frac{A}{2}, 4 R \cos \frac{B}{2}\hspace{1mm}$ & $\hspace{1mm} 4 R \cos \frac{C}{2}$.

• $ I_{1}=4 R \sin \frac{A}{2} ; I I_{2}=4 R \sin \frac{B}{2} ; I I_{3}=4 R \sin \frac{C}{2}$.

• Incentre I of $\triangle A B C$ is the orthocentre of the excentral $\Delta I_1 I_2 I_3$.

Distance Between Special Points :

• Distance between circumcentre and orthocentre

$$\mathrm{OH}^{2}=\mathrm{R}^{2}(1-8 \cos \mathrm{A} \cos \mathrm{B} \cos \mathrm{C})$$

• Distance between circumcentre and incentre

$$\mathrm{OI}^{2}=\mathrm{R}^{2}\left(1-8 \sin \frac{\mathrm{A}}{2} \sin \frac{\mathrm{B}}{2} \sin \frac{\mathrm{C}}{2}\right)=\mathrm{R}^{2}-2 \mathrm{Rr}$$

• Distance between circumcentre and centroid

$$O G^{2}=R^{2}-\frac{1}{9}\left(a^{2}+b^{2}+c^{2}\right)$$