title: “Lata knowledge-route-Class10-Math1-2 Merged.Pdf(1)” type: “reveal” weight: 1
TRIGONOMETRY
TRIGONOMETRY
11.1 TRIGONOMETRY :
Trigonometry means, the science which deals with the measurement of triangles.
11.1 (a) Trigonometric Ratios :
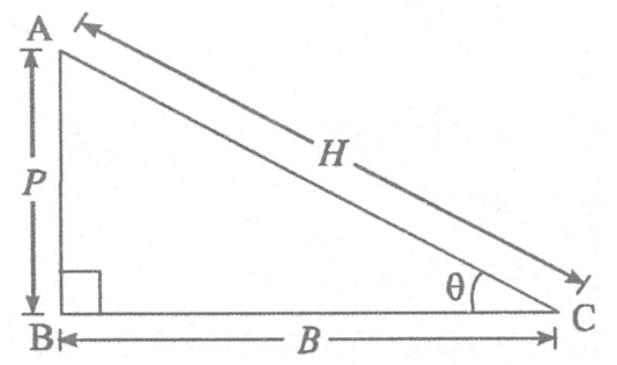
A right angled triangle is shown in Figure.
TRIGONOMETRY
(i) Six Trigonometry Ratio are :
TRIGONOMETRY
(ii) Interrelationship is Basic Trigonometric Ratio :
We also observe that
TRIGONOMETRY
11.1 (b) Trigonometric Table :
| Sin | |||||
| Cos | |||||
| Tan | Not defined |
||||
| Cot | Not defined |
||||
| Sec | Not defined |
||||
| Cosec | Not defined |
TRIGONOMETRY
11.1 (c) Trigonometric Identities :
(i)
(A)
(B)
(ii)
(A)
(B)
(C)
(iii)
(A)
(B)
(C)
TRIGONOMETRY
11.1 (d) Trigonometric Ratio of Complementary Angles :
TRIGONOMETRY
ILLUSTRATIONS :
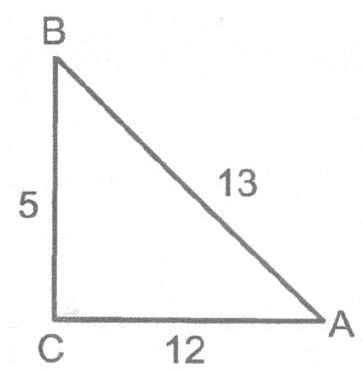
Ex. 1 In the given triangle
TRIGONOMETRY
Sol. Using Pythagoras theorem
TRIGONOMETRY
TRIGONOMETRY
Ex. 2 If
TRIGONOMETRY
Sol. Let
TRIGONOMETRY
Ex. 3 If
TRIGONOMETRY
Sol. We hare coses
So, we draw a right triangle
TRIGONOMETRY
L.H.S.
TRIGONOMETRY
R.H.S.
So, L.H.S. = R.H.S.
Hence Proved.
TRIGONOMETRY
Ex. 4 In
TRIGONOMETRY
Sol. In
TRIGONOMETRY
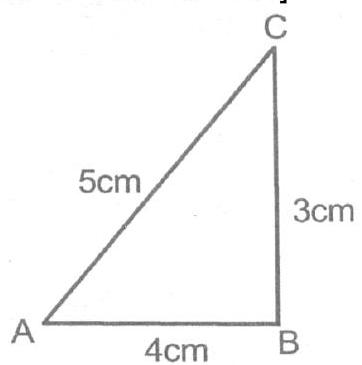
Now,
So,
TRIGONOMETRY
Ex. 5 Given that
TRIGONOMETRY
Sol. Putting
We get
TRIGONOMETRY
Ex. 6 A Rhombus of side of
TRIGONOMETRY
Sol. Let
In right triangle
TRIGONOMETRY
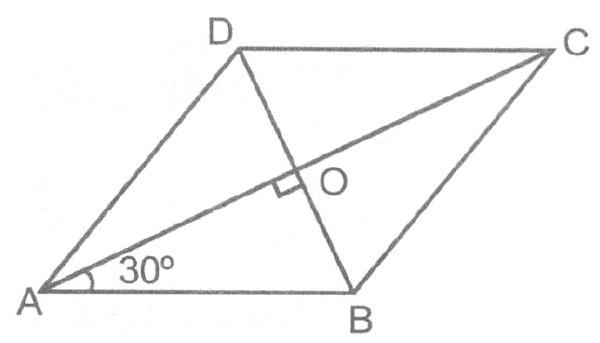
So, the length of diagonals
Area of Rhombus
TRIGONOMETRY
Ex. 7 Evaluate :
TRIGONOMETRY
Sol.
TRIGONOMETRY
Ex. 8 Prove that :
TRIGONOMETRY
Sol.
TRIGONOMETRY
Ex. 9 Prove that :
TRIGONOMETRY
Sol. L.H.S.
TRIGONOMETRY
Ex. 10 Prove that:
TRIGONOMETRY
Sol. L.H.S.
R.H.S. Hence Proved
TRIGONOMETRY
Ex. 11 If
TRIGONOMETRY
Sol. L.H.S.
TRIGONOMETRY
Ex. 12 If
TRIGONOMETRY
Sol.
TRIGONOMETRY
Adding equation (i) and (ii)
Adding equation (i) and (ii)
Ex. 13 If
TRIGONOMETRY
Sol. We have,
TRIGONOMETRY
TRIGONOMETRY
DAILY PRACTIVE PROBLEMS 11
OBJECTIVE DPP - 11.1
1. If
(A)
(B)
(C)
(D)
TRIGONOMETRY
| Qus. | 1 |
|---|---|
| Ans. | B |
TRIGONOMETRY
2. If
(A)
(B)
(C)
(D)
TRIGONOMETRY
| Qus. | 2 |
|---|---|
| Ans. | B |
TRIGONOMETRY
3. If
(A) 1
(B) 2
(C) 3
(D) 4
TRIGONOMETRY
| Qus. | 3 |
|---|---|
| Ans. | B |
TRIGONOMETRY
4. Given
(A) 9
(B)
(C)
(D)
TRIGONOMETRY
| Qus. | 4 |
|---|---|
| Ans. | A |
TRIGONOMETRY
5. If
(A) 0
(B)
(C)
(D) 1
TRIGONOMETRY
| Qus. | 5 |
|---|---|
| Ans. | D |
TRIGONOMETRY
6. The value of
(A) 1
(B) 2
(C) 3
(D) None of these
TRIGONOMETRY
| Qus. | 6 |
|---|---|
| Ans. | A |
TRIGONOMETRY
7. As
(A) increases
(B) decreases
(C) remains constant
(D) increases, then decreases
TRIGONOMETRY
| Qus. | 7 |
|---|---|
| Ans. | B |
TRIGONOMETRY
8. Find the value of
(A) 4
(B) 6
(C) - 2
(D) 0
TRIGONOMETRY
| Qus. | 8 |
|---|---|
| Ans. | B |
TRIGONOMETRY
9. The area of a triangle is
(A)
(B)
(C)
(D)
TRIGONOMETRY
| Qus. | 9 |
|---|---|
| Ans. | D |
TRIGONOMETRY
10. If
(A)
(B) 0
(C) 1
(D) 2
TRIGONOMETRY
| Qus. | 10 |
|---|---|
| Ans. | A |
TRIGONOMETRY
SUBJECTIVE DPP - 11.2
1. Evaluate : (A)
(B)
(C)
(D)
(E)
TRIGONOMETRY
| Qus. 1 | Ans. |
|---|---|
| (A) | 2 |
| (B) | 0 |
| (C) | 1 |
| (D) |
TRIGONOMETRY
2. If
TRIGONOMETRY
3. If
TRIGONOMETRY
4. If
(i)
TRIGONOMETRY
Prove the following (Q, 5 to Q. 13)
5.
TRIGONOMETRY
6.
[CBSE - 2008]
TRIGONOMETRY
7.
TRIGONOMETRY
8.
TRIGONOMETRY
9.
TRIGONOMETRY
10.
TRIGONOMETRY
11.
TRIGONOMETRY
12.
TRIGONOMETRY
13.
TRIGONOMETRY
14. If
TRIGONOMETRY
15. If
TRIGONOMETRY
16. If
[CBSE - 2004]
TRIGONOMETRY
17. Prove that :
[CBSE - 2005]
TRIGONOMETRY
18. Prove that :
[CBSE - 2005]
TRIGONOMETRY
19. Prove :
[CBSE - 2006]
TRIGONOMETRY
20. Evaluate :
[CBSE - 2007]
TRIGONOMETRY
| Qus. | 20 |
|---|---|
| Ans. |
TRIGONOMETRY
21. Without using trigonometric tables, evaluate the following :
[CBSE - 2008]
TRIGONOMETRY
| Qus. | 21 |
|---|---|
| Ans. | 2 |
TRIGONOMETRY
22. If
[CBSE - 2008]
TRIGONOMETRY
| Qus. | 22 |
|---|---|
| Ans. |
TRIGONOMETRY
23. If
[CBSE - 2008]
TRIGONOMETRY
| Qus. | 23 |
|---|---|
| Ans. |
TRIGONOMETRY
24. If
[CBSE - 2008]
TRIGONOMETRY
25. Prove :










