6.1 INTRODUCTION
A triangle, you have seen, is a simple closed curve made of three line segments. It has three vertices, three sides and three angles. Here is
Fig 6.1
The side opposite to the vertex A is
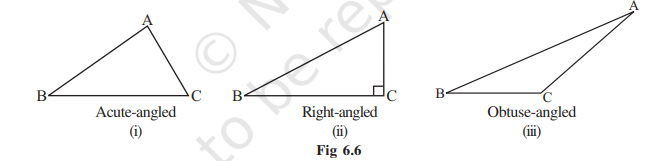
(i) Based on Sides: Scalene, Isosceles and Equilateral triangles.
(ii) Based on Angles: Acute-angled, Obtuse-angled and Right-angled triangles.
Make paper-cut models of the above triangular shapes. Compare your models with those of your friends and discuss about them.
TRY THESE
1. Write the six elements (i.e., the 3 sides and the 3 angles) of
2. Write the:
(i) Side opposite to the vertex
(ii) Angle opposite to the side
(iii) Vertex opposite to the side RT of
3. Look at Fig 6.2 and classify each of the triangles according to its
(a) Sides
(b) Angles
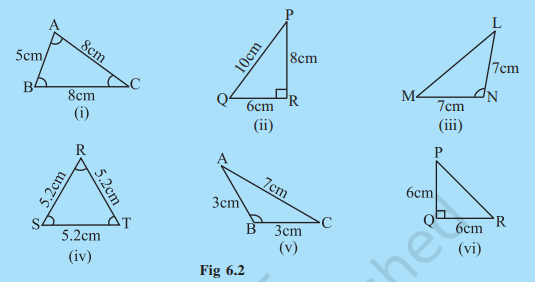
Now, let us try to explore something more about triangles.
6.2 MEDIANS OF A TRIANGLE
Given a line segment, you know how to find its perpendicular bisector by paper folding. Cut out a triangle
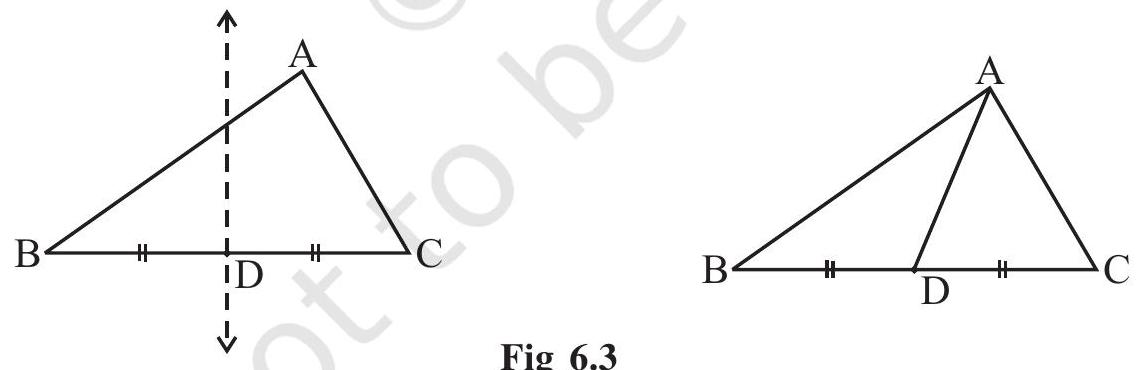
The line segment
Consider the sides
A median connects a vertex of a triangle to the mid-point of the opposite side.
THINK, DISCUSS AND WRITE
1. How many medians can a triangle have?
2. Does a median lie wholly in the interior of the triangle? (If you think that this is not true, draw a figure to show such a case).
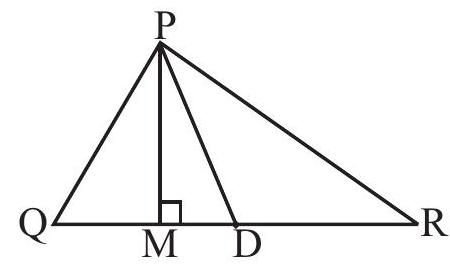
6.3 ALTITUDES OF A TRIANGLE
Make a triangular shaped cardboard ABC. Place it upright on a table. How ’tall’ is the triangle? The height is the distance from vertex A (in the Fig 6.4) to the base
From
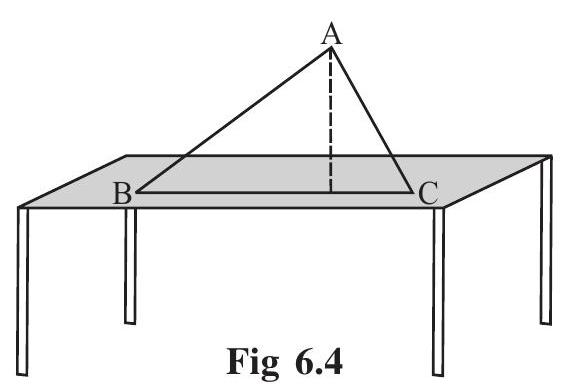 will represent its height?
will represent its height?
The height is given by the line segment that starts from
An altitude has one end point at a vertex of the triangle and the other on the line containing the opposite side. Through
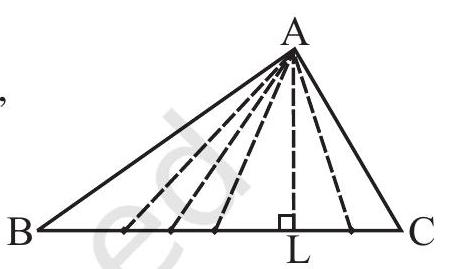
Fig 6.5 each vertex, an altitude can be drawn.
THINK, DISCUSS AND WRITE
1. How many altitudes can a triangle have?
2. Draw rough sketches of altitudes from A to
3. Will an altitude always lie in the interior of a triangle? If you think that this need not be true, draw a rough sketch to show such a case.
4. Can you think of a triangle in which two altitudes of the triangle are two of its sides?
5. Can the altitude and median be same for a triangle?
(Hint: For Q.No. 4 and 5, investigate by drawing the altitudes for every type of triangle).
DO THIS
Take several cut-outs of
(i) an equilateral triangle
(ii) an isosceles triangle and
(iii) a scalene triangle.
Find their altitudes and medians. Do you find anything special about them? Discuss it with your friends.
EXERCISE 6.1
1. In
Is
2. Draw rough sketches for the following:
(a) In
(b) In
(c) In
3. Verify by drawing a diagram if the median and altitude of an isosceles triangle can be same.
6.4 EXTERIOR ANGLE OF A TRIANGLE AND ITS PROPERTY
DO THIS
1. Draw a triangle
Clearly
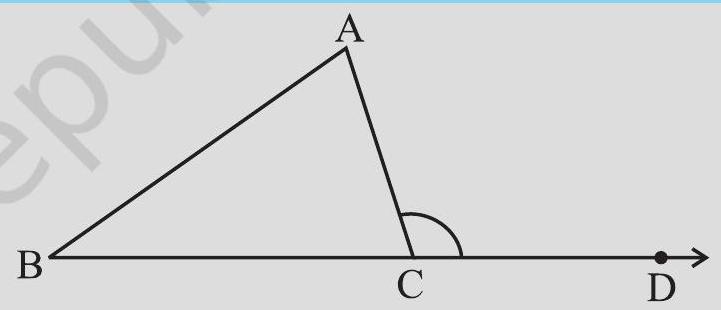
Fig 6.7
Do these two pieces together entirely cover
Can you say that
2. As done earlier, draw a triangle
Find the sum
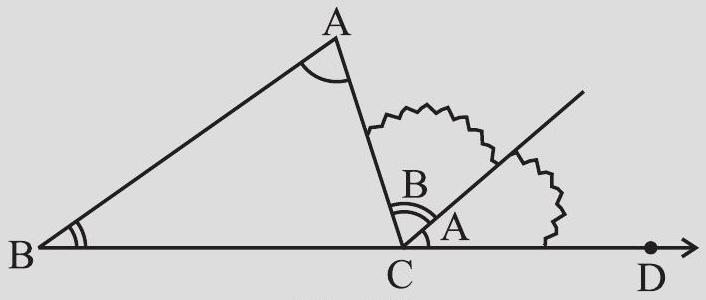
Fig 6.8
You may repeat the two activities as mentioned by drawing some more triangles along with their exterior angles. Every time, you will find that the exterior angle of a triangle is equal to the sum of its two interior opposite angles.
A logical step-by-step argument can further confirm this fact. angles.
An exterior angle of a triangle is equal to the sum of its interior opposite angles.
Given: Consider
To Show:
Through
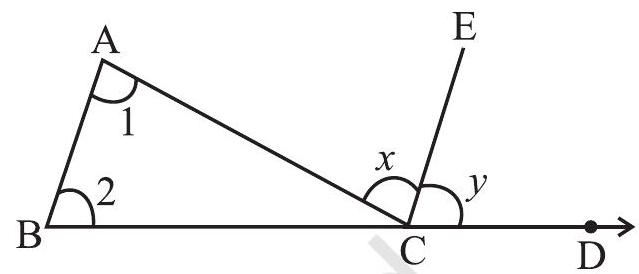
Fig 6.9
Justification
Steps
(a)
(b)
(c)
(d) Now,
Hence,
Reasons
Therefore, alternate angles should be equal.
Therefore, corresponding angles should be equal.
From Fig 6.9
The above relation between an exterior angle and its two interior opposite angles is referred to as the Exterior Angle Property of a triangle.
THINK, DISCUSS AND WRITE
1. Exterior angles can be formed for a triangle in many ways. Three of them are shown here (Fig 6.10)

There are three more ways of getting exterior angles. Try to produce those rough sketches.
2. Are the exterior angles formed at each vertex of a triangle equal?
3. What can you say about the sum of an exterior angle of a triangle and its adjacent interior angle?
Example 1 Find angle
Solution
Sum of interior opposite angles
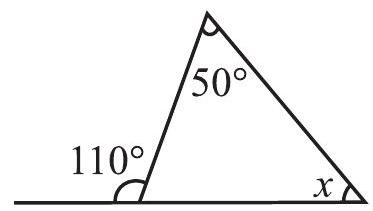
Fig 6.11
THINK, DISCUSS AND WRITE
1. What can you say about each of the interior opposite angles, when the exterior angle is
(i) a right angle?
(ii) an obtuse angle?
(iii) an acute angle?
2. Can the exterior angle of a triangle be a straight angle?
TRY THESE
1. An exterior angle of a triangle is of measure
2. The two interior opposite angles of an exterior angle of a triangle are
3. Is something wrong in this diagram (Fig 6.12)? Comment.
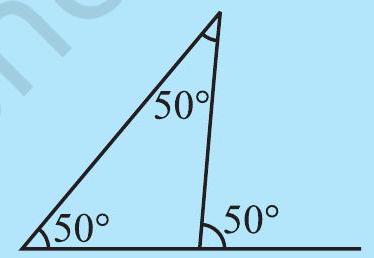
Fig 6.12
EXERCISE 6.2
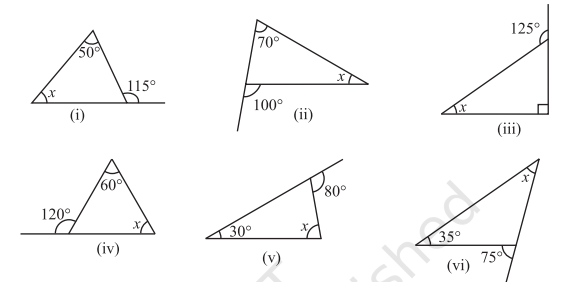
1. Find the value of the unknown exterior angle
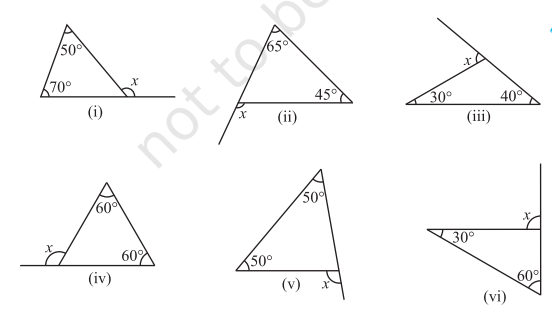
2. Find the value of the unknown interior angle
6.5 ANGLE SUM PROPERTY OF A TRIANGLE
There is a remarkable property connecting the three angles of a triangle. You are going to see this through the following four activities.
1. Draw a triangle. Cut on the three angles. Rearrange them as shown in Fig 6.13 (i), (ii). The three angles now constitute one angle. This angle is a straight angle and so has measure
(i)
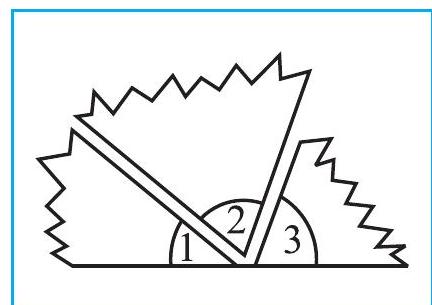
Fig 6.13
Thus, the sum of the measures of the three angles of a triangle is
2. The same fact you can observe in a different way also. Take three copies of any triangle, say

Fig 6.14
Arrange them as in Fig 6.15.
What do you observe about
(Do you also see the ’exterior angle property’?)
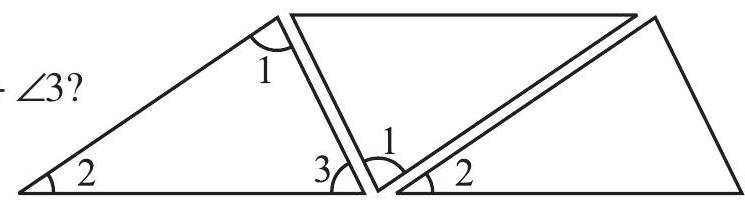
Fig 6.15
3. Take a piece of paper and cut out a triangle, say,
Make the altitude
Fold now the three corners such that all the three vertices A, B and C touch at M.
(i)
(ii)
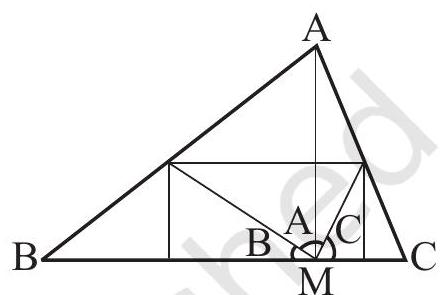
(iii)
Fig 6.16
You find that all the three angles form together a straight angle. This again shows that the sum of the measures of the three angles of a triangle is
4. Draw any three triangles, say
Use your protractor and measure each of the angles of these triangles.
Tabulate your results
| Name of |
Measures of Angles | Sum of the Measures of the three Angles |
|
|---|---|---|---|
Allowing marginal errors in measurement, you will find that the last column always gives
When perfect precision is possible, this will also show that the sum of the measures of the three angles of a triangle is
You are now ready to give a formal justification of your assertion through logical argument.
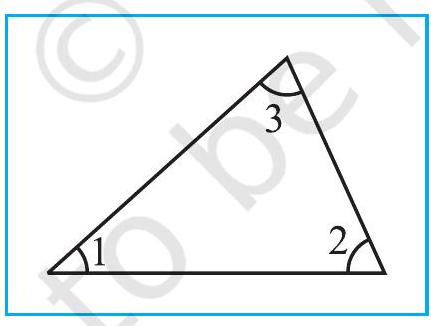
Statement The total measure of the three angles of a triangle is
To justify this let us use the exterior angle property of a triangle.
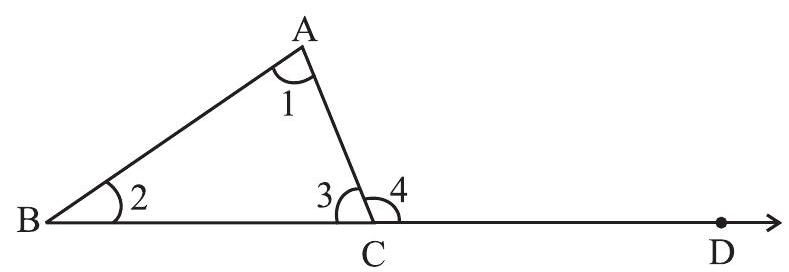
Fig 6.17
Given
Justification
But
Let us see how we can use this property in a number of ways.
Example 2 In the given figure (Fig 6.18) find
Solution
By angle sum property of a triangle,
Therefore
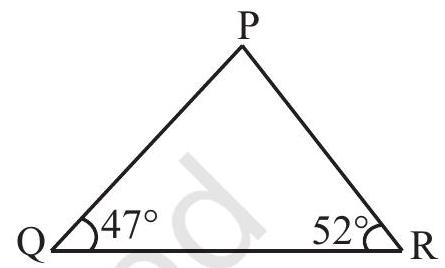
Fig 6.18
EXERCISE 6.3
1. Find the value of the unknown
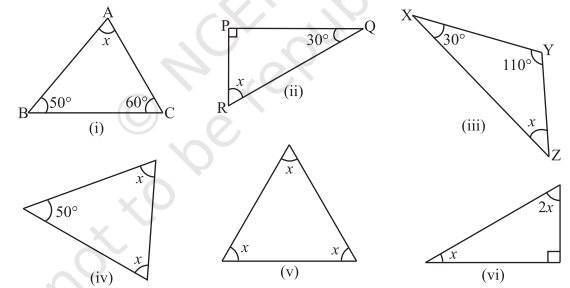
2. Find the values of the unknowns
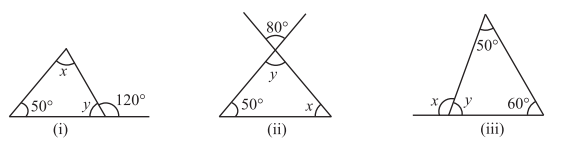
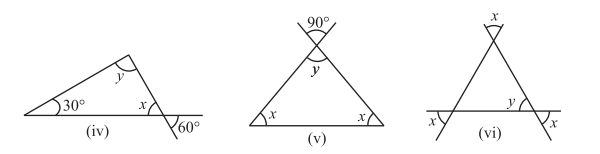
TRY THESE
1. Two angles of a triangle are
2. One of the angles of a triangle is
3. The three angles of a triangle are in the ratio
THINK, DISCUSS AND WRITE
1. Can you have a triangle with two right angles?
2. Can you have a triangle with two obtuse angles?
3. Can you have a triangle with two acute angles?
4. Can you have a triangle with all the three angles greater than
5. Can you have a triangle with all the three angles equal to
6. Can you have a triangle with all the three angles less than
6.6 TWO SPECIAL TRIANGIES : EGULLATERAL AND ISOSCELES
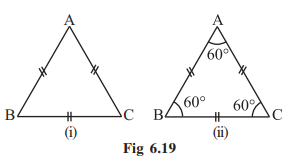
A triangle in which all the three sides are of equal lengths is called an equilateral triangle.
Take two copies of an equilateral triangle ABC (Fig 6.19). Keep one of them fixed. Place the second triangle on it. It fits exactly into the first. Turn it round in any way and still they fit with one another exactly. Are you able to see that when the three sides of a triangle have equal lengths then the three angles are also of the same size?
We conclude that in an equilateral triangle:
(i) all sides have same length.
(ii) each angle has measure
A triangle in which two sides are of equal lengths is called an isosceles triangle.
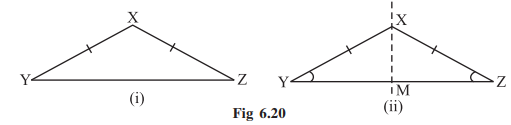
Fig 6.20
From a piece of paper cut out an isosceles triangle XYZ, with XY=XZ (Fig 6.20). Fold it such that
Thus, in an isosceles triangle:
(i) two sides have same length.
(ii) base angles opposite to the equal sides are equal.
TRY THESE
1. Find angle x is each figure:
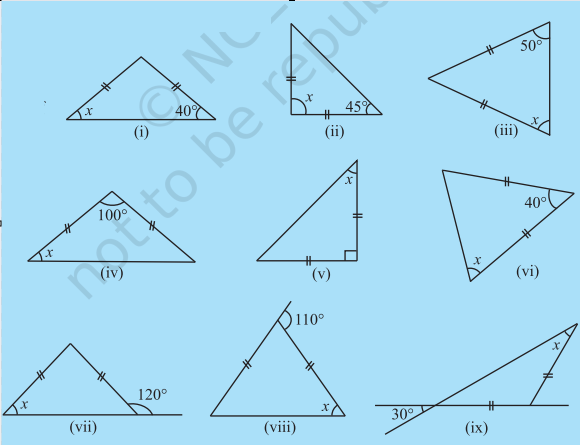
2. Find angles
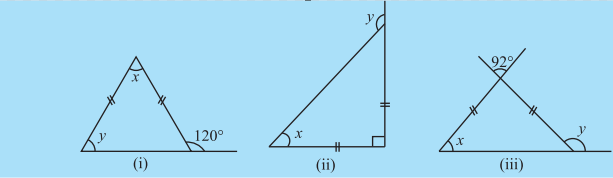
6.7 SUM OF THE LENGTHS OF TWO SIDES OF A TRIANGLE
1. Mark three non-collinear spots A, B and C in your playground. Using lime powder mark the paths
Ask your friend to start from
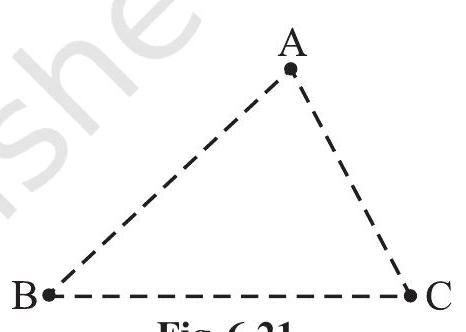
Fig 6.21
Similarly, if one were to start from
By a similar argument, you find that
These observations suggest that the sum of the lengths of any two sides of a triangle is greater than the third side.
2. Collect fifteen small sticks (or strips) of different lengths, say,
Take any three of these sticks and try to form a triangle. Repeat this by choosing different combinations of three sticks.
Suppose you first choose two sticks of length
To form a triangle you will need any three sticks such that the sum of the lengths of any two of them will always be greater than the length of the third stick.
This also suggests that the sum of the lengths of any two sides of a triangle is greater than the third side.
3. Draw any three triangles, say
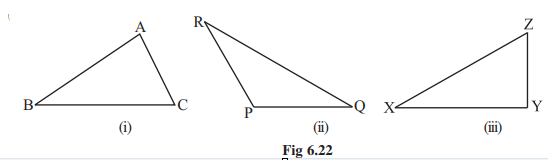
Fig 6.22
Use your ruler to find the lengths of their sides and then tabulate your results as follows:
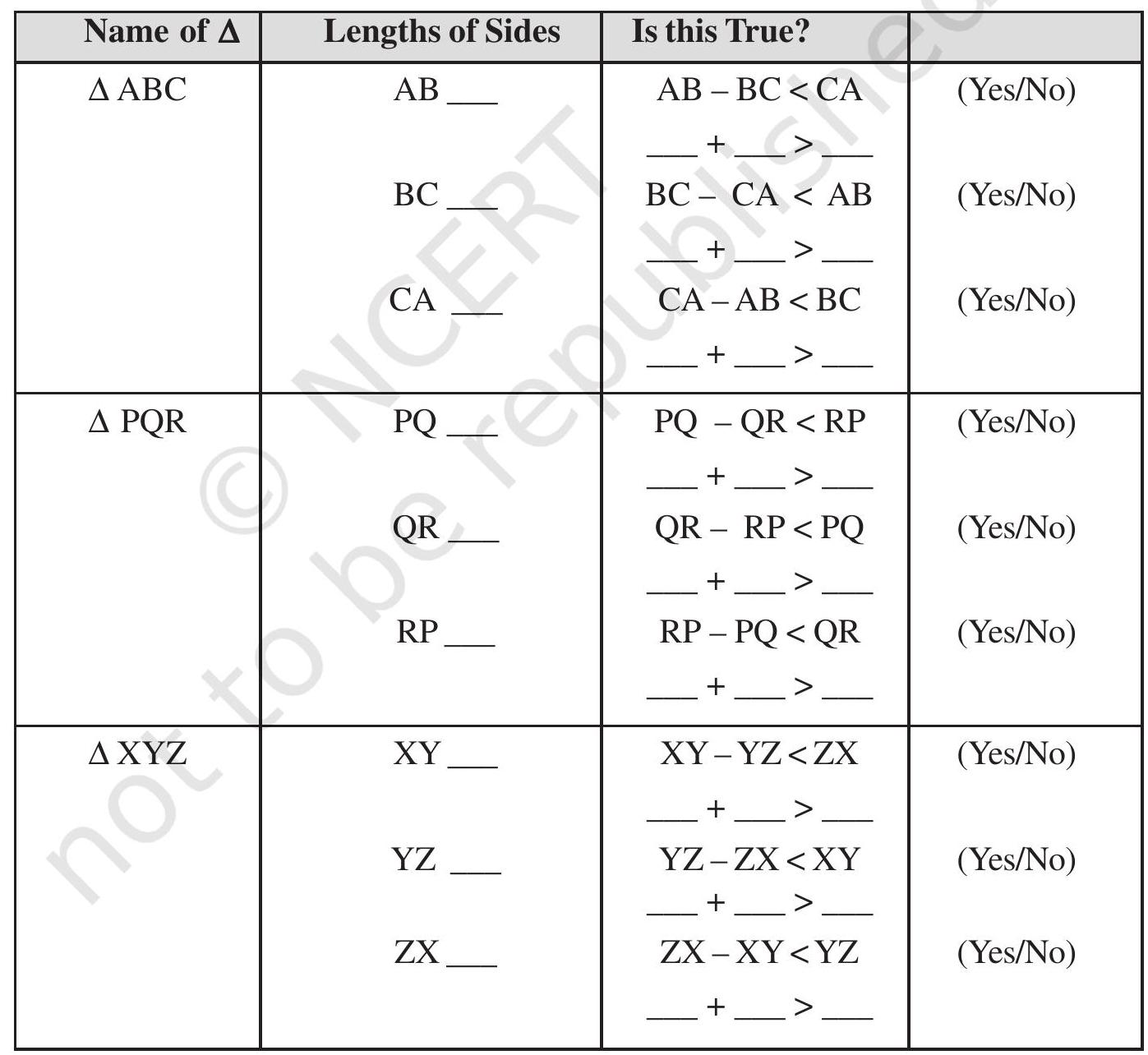
This also strengthens our earlier guess. Therefore, we conclude that sum of the lengths of any two sides of a triangle is greater than the length of the third side.
We also find that the difference between the length of any two sides of a triangle is smaller than the length of the third side.
EXAmple 3Is there a triangle whose sides have lengths
Solution Suppose such a triangle is possible. Then the sum of the lengths of any two sides would be greater than the length of the third side. Let us check this.
Therefore, the triangle is possible.
Example 4 The lengths of two sides of a triangle are
Solution
We know that the sum of two sides of a triangle is always greater than the third.
Therefore, third side has to be less than the sum of the two sides. The third side is thus, less than
The side cannot be less than the difference of the two sides. Thus, the third side has to be more than
The length of the third side could be any length greater than 2 and less than
EXERCISE 6.4
1. Is it possible to have a triangle with the following sides?
(i)
2. Take any point
(i)
(ii)
(iii)
3.
Is
(Consider the sides of triangles
4.
Is
5.
6. The lengths of two sides of a triangle are
THINK, DISCUSS AND WRITE
1. Is the sum of any two angles of a triangle always greater than the third angle?
6.8 RIGHT-ANGLED TRIANGLES AND PYTHAGORAS PROPERTY
Pythagoras, a Greek philosopher of sixth century
B.C. is said to have found a very important and useful property of right-angled triangles given in this section. The property is, hence, named after him. In fact, this property was known to people of many other countries too. The Indian mathematician Baudhayan has also given an equivalent form of this property. We now try to explain the Pythagoras property.
In a right-angled triangle, the sides have some
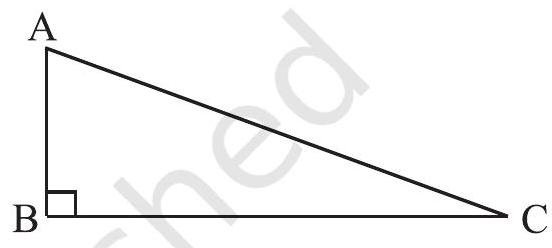
Fig 6.23 special names. The side opposite to the right angle is called the hypotenuse; the other two sides are known as the legs of the right-angled triangle.
In
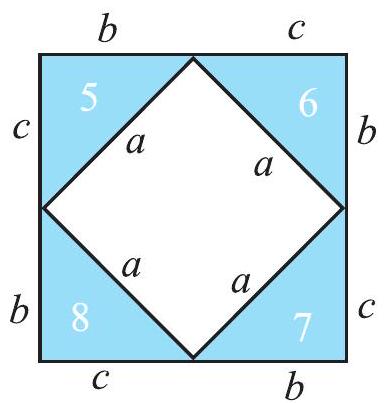
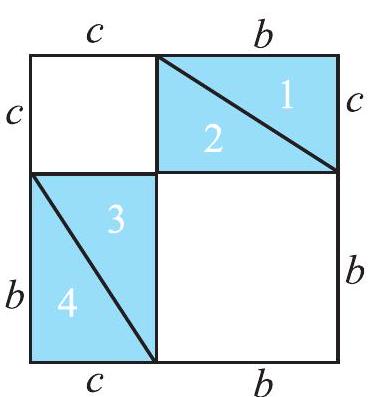
Make eight identical copies of right angled triangle of any size you prefer. For example, you make a right-angled triangle whose hypotenuse is
Draw two identical squares on a sheet with sides
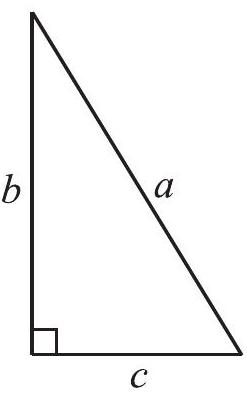
Fig 6.24 of lengths
You are to place four triangles in one square and the remaining four triangles in the other square, as shown in the following diagram (Fig 6.25).
Square A
Square B
Fig 6.25
The squares are identical; the eight triangles inserted are also identical.
Hence the uncovered area of square
i.e., Area of inner square of square
This is Pythagoras property. It may be stated as follows:
In a right-angled triangle,
the square on the hypotenuse
Pythagoras property is a very useful tool in mathematics. It is formally proved as a theorem in later classes. You should be clear about its meaning.
It says that for any right-angled triangle, the area of the square on the hypotenuse is equal to the sum of the areas of the squares on the legs.
Draw a right triangle, preferably on a square sheet, construct squares on its sides, compute the area of these squares and verify the theorem practically (Fig 6.26).
If you have a right-angled triangle, the Pythagoras property holds. If the Pythagoras property holds for some triangle, will the triangle be rightangled? (Such problems are known as converse problems). We will try to answer this. Now, we will show that, if there is a triangle such that sum of the squares on two of its sides is equal to the square of the third side, it must be a right-angled triangle.
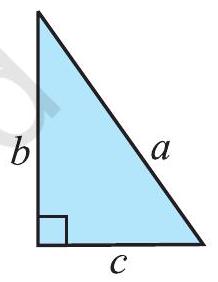
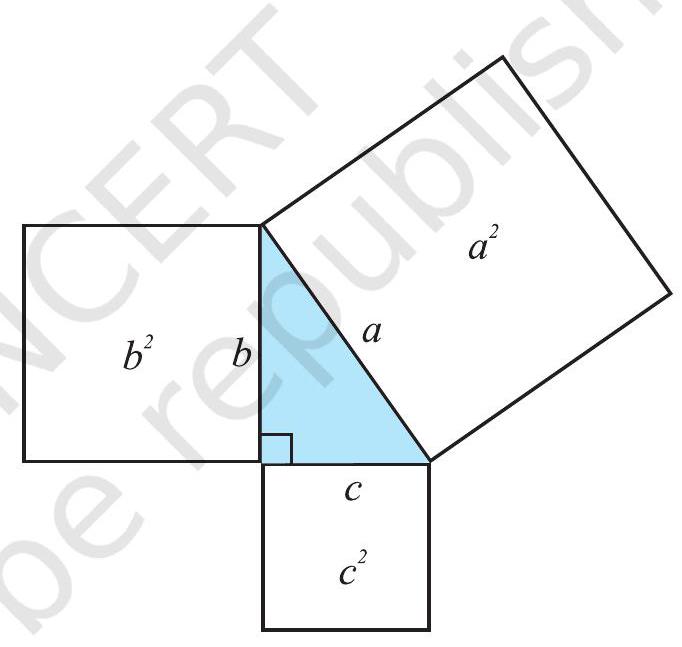
Fig 6.26
DO THIS
1. Have cut-outs of squares with sides
In fact, in this case each angle will be acute! Note that
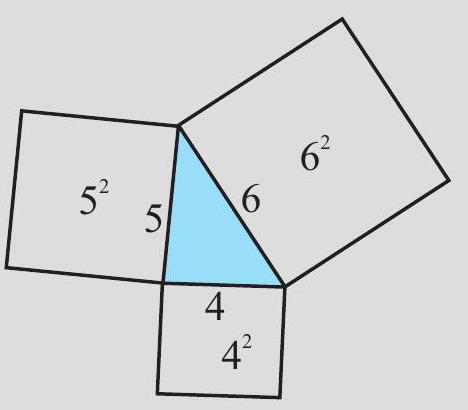
Fig 6.27
2. Repeat the above activity with squares whose sides have lengths
This shows that Pythagoras property holds if and only if the triangle is right-angled. Hence we get this fact:
If the Pythagoras property holds, the triangle must be right-angled.
Example 5 Determine whether the triangle whose lengths of sides are
Solution
We find
Therefore, the triangle is right-angled.
Note: In any right-angled triangle, the hypotenuse happens to be the longest side. In this example, the side with length
Example 6
Solution
A rough figure will help us (Fig 6.28).
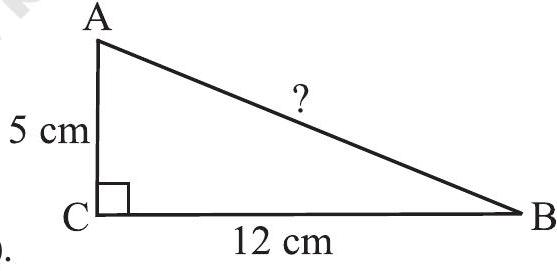
Fig 6.28
By Pythagoras property,
or
or the length of
Note: To identify perfect squares, you may use prime factorisation technique.
TRY THESE
Find the unknown length
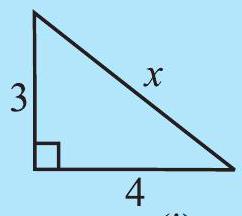
(i)
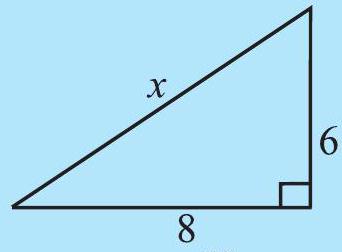
(ii)
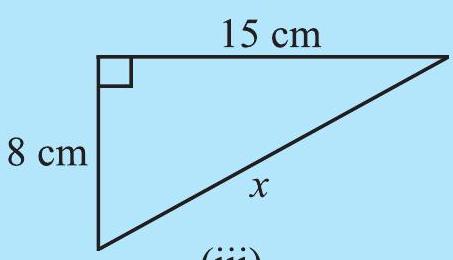
(iii)
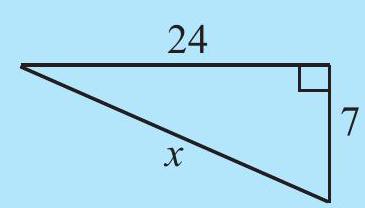
(iv)
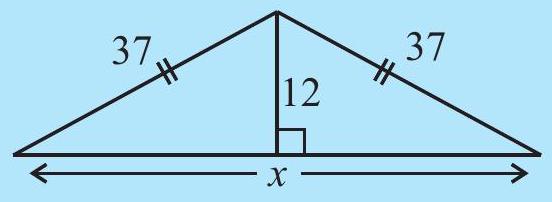
(v)
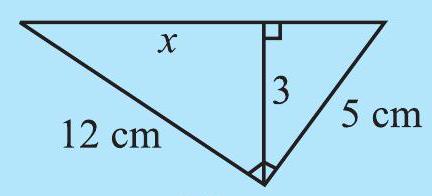
(vi)
Fig 6.29
EXERCISE 6.5
1.
2.
3. A
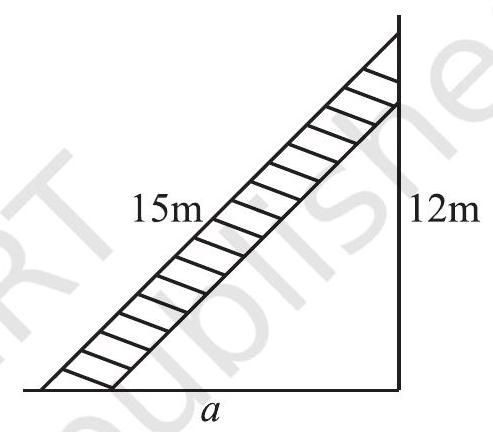
4. Which of the following can be the sides of a right triangle?
(i)
(ii)
(iii)
In the case of right-angled triangles, identify the right angles.
5. A tree is broken at a height of
6. Angles
(i)
(ii)
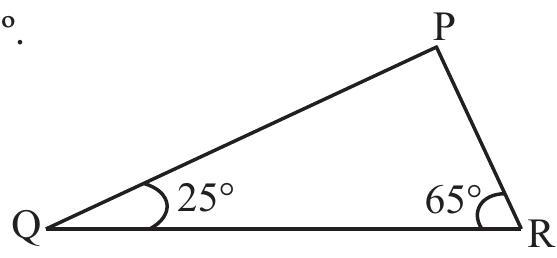
(iii)
7. Find the perimeter of the rectangle whose length is
8. The diagonals of a rhombus measure
THINK, DISCUSS AND WRITE
1. Which is the longest side in the triangle
2. Which is the longest side in the triangle
3. Which is the longest side of a right triangle?
4. ‘The diagonal of a rectangle produce by itself the same area as produced by its length and breadth’- This is Baudhayan Theorem. Compare it with the Pythagoras property.
DO THIS
Enrichment activity
There are many proofs for Pythagoras theorem, using ‘dissection’ and ‘rearrangement’ procedure. Try to collect a few of them and draw charts explaining them.
What have We Discussed?
1. The six elements of a triangle are its three angles and the three sides.
2. The line segment joining a vertex of a triangle to the mid point of its opposite side is called a median of the triangle. A triangle has 3 medians.
3. The perpendicular line segment from a vertex of a triangle to its opposite side is called an altitude of the triangle. A triangle has 3 altitudes.
4. An exterior angle of a triangle is formed, when a side of a triangle is produced. At each vertex, you have two ways of forming an exterior angle.
5. A property of exterior angles:
The measure of any exterior angle of a triangle is equal to the sum of the measures of its interior opposite angles.
6. The angle sum property of a triangle:
The total measure of the three angles of a triangle is
7. A triangle is said to be equilateral, if each one of its sides has the same length.
In an equilateral triangle, each angle has measure
8. A triangle is said to be isosceles, if atleast any two of its sides are of same length.
The non-equal side of an isosceles triangle is called its base; the base angles of an isosceles triangle have equal measure.
9. Property of the lengths of sides of a triangle:
The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
The difference between the lengths of any two sides is smaller than the length of the third side.
This property is useful to know if it is possible to draw a triangle when the lengths of the three sides are known.
10. In a right angled triangle, the side opposite to the right angle is called the hypotenuse and the other two sides are called its legs.
11. Pythagoras property:
In a right-angled triangle,
the square on the hypotenuse
If a triangle is not right-angled, this property does not hold good. This property is useful to decide whether a given triangle is right-angled or not.






