Work Power and Energy 4 Question 4
5. A stone tied to a string of length
(a)
(b)
(c)
(d)
(1998, 2M)
Show Answer
Answer:
Correct Answer: 5. (d)
Solution:
- From energy conservation,
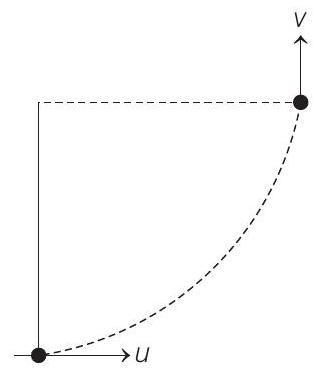
Now, since the two velocity vectors shown in figure are mutually perpendicular, hence the magnitude of change of velocity will be given by
Substituting value of
or
Therefore, tangential acceleration,
or
Only tangential force does work.






