SATHEE: Work Power and Energy 1 Question 4

Work Power and Energy 1 Question 4

5. The work done on a particle of mass $m$ by a force, $K \frac{x}{{(x^{2} + y^{2})}^{3 / 2}} \hat{i} + \frac{y}{{(x^{2} + y^{2})}^{3 / 2}} \hat{j}$

$(K$ being a

constant of appropriate dimensions), when the particle is taken from the point $(a, 0)$ to the point $(0, a)$ along a circular path of radius $a$ about the origin in the $x - y$ plane is

(2013 Adv.)

(a) $\frac{2 K π}{a}$

(b) $\frac{K π}{a}$

(c) $\frac{K π}{2 a}$

(d) 0

Show Answer

Answer:

Correct Answer: 5. (d)

Solution:

$r = O P = x \hat{i} + y \hat{j}$

$F = \frac{k}{{(x^{2} + y^{2})}^{3 / 2}} (x \hat{i} + y \hat{j}) = \frac{k}{r^{3}} (r)$

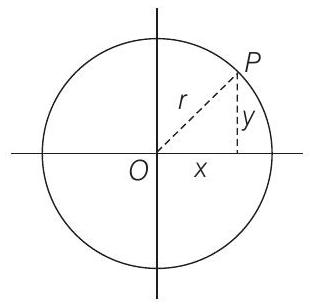
Since, $F$ is along $r$ or in radial direction.

Therefore, work done is zero.

पिछला

अगला

गोपनीयता नीति

द्वारा संचालित Prutor@IITK

sathee@iitk.ac.in

SATHEE का मीडिया कवरेज

खेल स्टोर

ऐप स्टोर

Ask SATHEE

Welcome to SATHEE !
Select from 'Menu' to explore our services, or ask SATHEE to get started. Let's embark on this journey of growth together! 🌐📚🚀🎓

I'm relatively new and can sometimes make mistakes.
If you notice any error, such as an incorrect solution, please use the thumbs down icon to aid my learning.
To begin your journey now, click on "I understand".

Work Power and Energy 1 Question 4

5. The work done on a particle of mass m by a force, Kx(x2+y2)3/2i^+y(x2+y2)3/2j^

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu

5. The work done on a particle of mass $m$ by a force, $K \frac{x}{{(x^{2} + y^{2})}^{3 / 2}} \hat{i} + \frac{y}{{(x^{2} + y^{2})}^{3 / 2}} \hat{j}$