SATHEE: Work Power and Energy 1 Question 1

Work Power and Energy 1 Question 1

1. A uniform cable of mass $M$ and length $L$ is placed on a horizontal surface such that its $\frac{1}{n}$ th part is hanging below the edge of the surface. To lift the hanging part of the cable upto the surface, the work done should be

(2019 Main, 9 April I)

(a) $\frac{2 M g L}{n^{2}}$

(b) $n M g L$

(d) $\frac{M g L}{2 n^{2}}$

Show Answer

Answer:

Correct Answer: 1. (d)

Solution:

Given, mass of the cable is $M$ .

So, mass of $\frac{1}{n}$ th part of the cable, i.e. hanged part of the cable is

$= M / n$

Now, centre of mass of the hanged part will be its middle point. So, its distance from the top of the table will be $L / 2 n$ .

$∴$ Initial potential energy of the hanged part of cable,

$\begin{aligned} U_{i} & = \frac{M}{n} (- g) \frac{L}{2 n} \\ \Rightarrow U_{i} & = - \frac{M g L}{2 n^{2}} \end{aligned}$

When whole cable is on the table,

its potential energy will be zero.

$∴ U_{f} = 0$

Now, using work-energy theorem,

$\begin{aligned} W_{net} = Δ U = U_{f} - U_{i} \\ \Rightarrow W_{net} = 0 - \frac{M g L}{2 n^{2}} \\ \Rightarrow W_{net} = \frac{M g L}{2 n^{2}} \end{aligned}$

[using Eqs. (ii) and (iii)]

2 Normal reaction force on the block is

$N = m a_{net}$

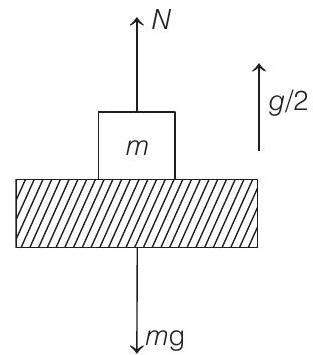
where, $a_{net} =$ net acceleration of block.

$\begin{aligned} = g + a = g + \frac{g}{2} = \frac{3 g}{2} \\ \Rightarrow N & = m g + \frac{g}{2} = \frac{3 m g}{2} \end{aligned}$

Now, in time ’ $t$ ’ block moves by a displacement $s$ given by

$s = 0 + \frac{1}{2} a t^{2} = \frac{1}{2} \frac{g}{2} t^{2} (∵ u = 0)$

Here, $a = \frac{g}{2}$ (given)

$∴$ Work done $=$ Force $\times$ Displacement

$\Rightarrow W = \frac{3 m g}{2} \times \frac{g t^{2}}{4} = \frac{3 m g^{2} t^{2}}{8} .$

पिछला

अगला

Work Power and Energy 1 Question 1

1. A uniform cable of mass $M$ and length $L$ is placed on a horizontal surface such that its $\frac{1}{n}$ th part is hanging below the edge of the surface. To lift the hanging part of the cable upto the surface, the work done should be

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Work Power and Energy 1 Question 1

1. A uniform cable of mass M and length L is placed on a horizontal surface such that its 1n th part is hanging below the edge of the surface. To lift the hanging part of the cable upto the surface, the work done should be

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu

1. A uniform cable of mass $M$ and length $L$ is placed on a horizontal surface such that its $\frac{1}{n}$ th part is hanging below the edge of the surface. To lift the hanging part of the cable upto the surface, the work done should be