Wave Motion 5 Question 7
7. The displacement
This expression may be considered to be a result of the superposition of independent harmonic motions.
(a) two
(b) three
(c) four
(d) five
Passage Based Questions
Passage 1
Two trains
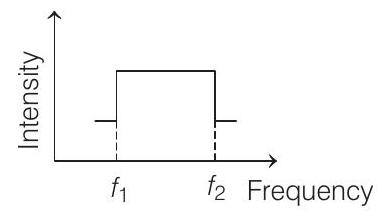
Assume that the sound of the whistle is composed of components varying in frequency from
Show Answer
Solution:
- The given equation can be written as
i.e. the given expression is a result of superposition of three independent harmonic motions of angular frequencies 999, 1000 and






