Wave Motion 4 Question 7
7. A musician produce the sound of second harmonics from open end flute of $50 cm$. The other person moves toward the musician with speed $10 km / h$ from the second end of room. If the speed of sound $330 m / s$, the frequency heard by running person will be
(2019 Main, 9 Jan II)
(a) $666 Hz$
(b) $500 Hz$
(c) $753 Hz$
(d) $333 Hz$
Show Answer
Solution:
- According to the question, the musician uses a open flute of length $50 cm$ and produce second harmonic sound waves
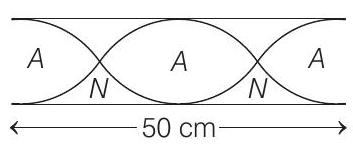
When the flute is open from both ends and produce second harmonic, then
$$ \begin{aligned} L & =\lambda _2 \\ \Rightarrow \quad f _2 & =\frac{v}{L} \end{aligned} $$
where, $\lambda _2=$ wavelength for second harmonic,
$$ f _2=\text { frequency for second harmonic } $$
and $\quad v=$ speed of wave.
For given question $\Rightarrow f _2=\frac{v}{L}=\frac{330}{50 \times 10^{-2}}$
$f _2=660 Hz$ (frequency produce by source)
Now, a person runs towards the musician from another end of a hall
$$ v _{\text {observer }}=10 km / h \text { (towards source) } $$
There is apparant change in frequency, which heard by person and given by Doppler’s effect formula
$$ \begin{aligned} \Rightarrow \quad v^{\prime} & =f^{\prime}=v\left[\frac{v _{\text {sound }}+v _{\text {observer }}}{v _{\text {sound }}}\right] \\ f^{\prime} & =f _2\left[\frac{v _s+v _o}{v _{\text {sound }}}\right] \\ f^{\prime} & =660\left[\frac{330+\frac{50}{18}}{330}\right] \\ f^{\prime} & =666 Hz \end{aligned} $$
Hence, option (a) is correct.
