Wave Motion 4 Question 28
26. A whistle emitting a sound of frequency
(1996, 3M)
Show Answer
Answer:
Correct Answer: 26. (b, c)
Solution:
Maximum frequency will be heard by the observer in position
where,
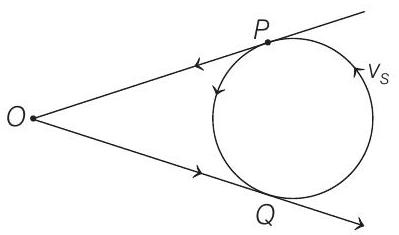
and
Therefore, range of frequencies heard by observer is from






