Wave Motion 4 Question 22
21. A stationary source emits sound of frequency $f _0=492 Hz$. The sound is reflected by a large car approaching the source with a speed of $2 ms^{-1}$. The reflected signal is received by the source and superposed with the original. What will be the beat frequency of the resulting signal in Hz? (Given that the speed of sound in air is $330 ms^{-1}$ and the car reflects the sound at the frequency it has received).
(2017 Adv.)
Show Answer
Answer:
Correct Answer: 21. (a)
Solution:
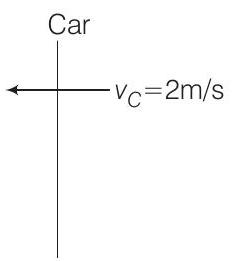
Frequency observed at car
$$ f _1=f _0\left(\frac{v+v _C}{v}\right) \quad(v=\text { speed of sound }) $$
Frequency of reflected sound as observed at the source
$$ f _2=f _1\left(\frac{v}{v-v _C}\right)=f _0\left(\frac{v+v _C}{v-v _C}\right) $$
Beat frequency $=f _2-f _0$
$$ \begin{aligned} & =f _0\left[\frac{v+v _C}{v-v _C}-1\right]=f _0\left[\frac{2 v _C}{v-v _C}\right] \\ & =492 \times \frac{2 \times 2}{328}=6 Hz \end{aligned} $$
