SATHEE: Wave Motion 2 Question 45

Wave Motion 2 Question 45

45. A metallic rod of length $1 m$ is rigidly clamped at its mid-point. Longitudinal stationary waves are set-up in the rod in such a way that there are two nodes on either side of the mid-point. The amplitude of an antinode is $2 \times 10^{- 6} m$ . Write the equation of motion at a point $2 c m$ from the mid-point and those of the constituent waves in the rod. (Young’s modulus of the material of the rod $= 2 \times 10^{11} N m^{- 2};$ density $= 8000 k g m^{- 3}$ )

(1994, 6M)

Show Answer

Answer:

Correct Answer: 45. $y = 2 \times 10^{- 6} \sin (0.1 π) \sin (25000 π t)$ ,

$y_{1} = 10^{- 6} \sin (25000 π t - 5 π x), y_{2} = 10^{- 6} \sin (25000 π t + 5 π x)$

Solution:

Speed of longitudinal travelling wave in the rod will be

$v = \sqrt{\frac{Y}{ρ}} = \sqrt{\frac{2 \times 10^{11}}{8000}} = 5000 m / s$

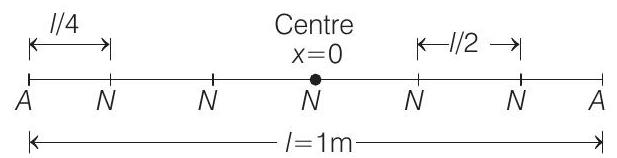
Amplitude at antinode $= 2 A$ (Here, $A$ is the amplitude of constituent waves )

$\begin{aligned} = 2 \times 10^{- 6} m \\ ∴ A = 10^{- 6} m \Rightarrow l = \frac{5 λ}{2} \\ \Rightarrow λ = \frac{2 l}{5} = \frac{(2) (1.0)}{5} m = 0.4 m \end{aligned}$

Hence, the equation of motion at a distance $x$ from the mid-point will be given by,

$\begin{aligned} \begin{aligned} y = 2 A \sin k x \sin ω t \\ Here, k = \frac{2 π}{0.4} = 5 π \\ ω = 2 π f = 2 π \frac{v}{λ} \\ = 2 π (\frac{5000}{0.4}) r a d / s = 25000 π \\ ∴ y = (2 \times 10^{- 6}) \sin (5 π x) \sin (25000 π t) \end{aligned} \end{aligned}$

Therefore, $y$ at a distance $x = 2 c m = 2 \times 10^{- 2} m$

$\begin{aligned} is y = 2 \times 10^{- 6} \sin (5 π \times 2 \times 10^{- 2}) \sin (25000 π t) \\ or y = 2 \times 10^{- 6} \sin (0.1 π) \sin (25000 π t) \end{aligned}$

The equations of constituent waves are

$\begin{aligned} y_{1} = A \sin (ω t - k x) and y_{2} = A \sin (ω t + k x) \\ or y_{1} = 10^{- 6} \sin (25000 π t - 5 π x) \\ and y_{2} = 10^{- 6} \sin (25000 π t + 5 π x) \end{aligned}$