SATHEE: Wave Motion 2 Question 43

Wave Motion 2 Question 43

43. A $3.6 m$ long pipe resonates with a source of frequency $212.5 H z$ when water level is at certain heights in the pipe. Find the heights of water level (from the bottom of the pipe) at which resonances occur. Neglect end correction. Now the pipe is filled to a height $H (\approx 3.6 m)$ . A small hole is drilled very close to its bottom and water is allowed to leak. Obtain an expression for the rate of fall of water level in the pipe as a function of $H$ . If the radii of the pipe and the hole are $2 \times 10^{- 2} m$ and $1 \times 10^{- 3} m$ respectively. Calculate the time interval between the occurrence of first two resonances. Speed of sound in air is $340 m / s$ and $g = 10 m / s^{2} (2000, 10 M)$

Show Answer

Answer:

Correct Answer: 43. $3.2 m, 2.4 m, 1.6 m, 0.8 m, - \frac{d H}{d t} = (1.11 \times 10^{- 2}) \sqrt{H}, 43 s$

Solution:

Speed of sound $v = 340 m / s$

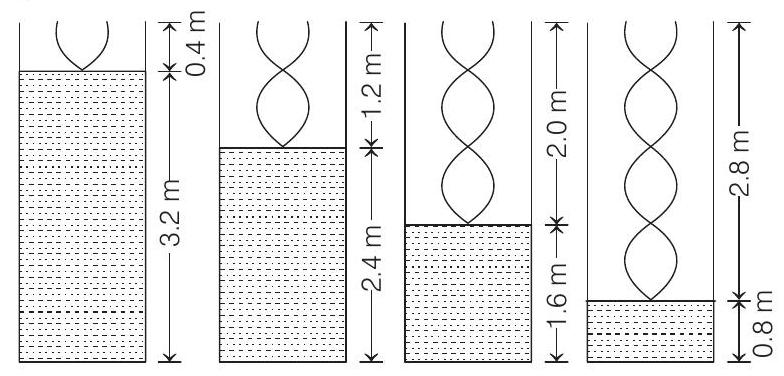
Let $l_{0}$ be the length of air column corresponding to the fundamental frequency. Then,

$\frac{v}{4 l_{0}} = 212.5 or l_{0} = \frac{v}{4 (212.5)} = \frac{340}{4 (212.5)} = 0.4 m$

In closed pipe only odd harmonics are obtained. Now let $l_{1}, l_{2}, l_{3}, l_{4}$ , etc., be the lengths corresponding to the $3 r d$ harmonic, 4th harmonic, 7th harmonic etc. Then,

$\begin{aligned} 3 (\frac{v}{4 l_{1}}) & = 212.5 \Rightarrow l_{1} = 1.2 m \\ 5 (\frac{v}{4 l_{2}}) & = 212.5 \Rightarrow l_{2} = 2.0 m \\ and 7 (\frac{v}{4 l_{3}}) & = 212.5 \Rightarrow l_{3} = 2.8 m \\ 9 (\frac{v}{4 l_{4}}) & = 212.5 \Rightarrow l_{4} = 3.6 m \end{aligned}$

or heights of water level are $(3.6 - 0.4) m, (3.6 - 1.2) m$ , $(3.6 - 2.0) m$ and $(3.6 - 2.8) m$ .

$∴$ Heights of water level are $3.2 m, 2.4 m, 1.6 m$ and $0.8 m$ . Let $A$ and $a$ be the area of cross-sections of the pipe and hole respectively. Then,

$\begin{aligned} A = π {(2 \times 10^{- 2})}^{2} = 1.26 \times 10^{- 3} m^{2} \\ and a = π {(10^{- 3})}^{2} = 3.14 \times 10^{- 6} m^{2} \end{aligned}$

Velocity of efflux, $v = \sqrt{2 g H}$

Continuity equation at 1 and 2 gives

$a \sqrt{2 g H} = A (\frac{- d H}{d t})$

$∴$ Rate of fall of water level in the pipe,

$(\frac{- d H}{d t}) = \frac{a}{A} \sqrt{2 g H}$

Substituting the values, we get

$\begin{aligned} \frac{- d H}{d t} & = \frac{3.14 \times 10^{- 6}}{1.26 \times 10^{- 3}} \sqrt{2 \times 10 \times H} \\ or - \frac{d H}{d t} & = (1.11 \times 10^{- 2}) \sqrt{H} \end{aligned}$

Between first two resonances, the water level falls from $3.2 m$ to $2.4 m$ .

$∴ \frac{d H}{\sqrt{H}} = - (1.11 \times 10^{- 2}) d t$

or $\int_{3.2}^{2.4} \frac{d H}{\sqrt{H}} = - (1.11 \times 10^{- 2}) \int_{0}^{t} d t$

or $2 [\sqrt{2.4} - \sqrt{3.2}] = - (1.11 \times 10^{- 2}) \cdot t$ or $t \approx 43 s$

NOTE

Rate of fall of level at a heighth is

$(\frac{- d h}{d t}) = \frac{a}{A} \sqrt{2 g h} \propto \sqrt{H}$

i.e., rate decreases as the height of water ( or any other liquid) decreases in the tank. That is why, the time required to empty the first half of the tank is less than the time required to empty the rest half of the tank.

पिछला

अगला