Wave Motion 2 Question 4
4. A wire of length $2 L$, is made by joining two wires $A$ and $B$ of same length but different radii $r$ and $2 r$
and made of the same material. It is vibrating at a frequency such that the joint of the two wires forms a node. If the number of antinodes in wire $A$ is $p$ and that in $B$ is $q$, then the ratio $p: q$ is
(2019 Main, 8 April I)
(a) $3: 5$
(b) $4: 9$
(c) $1: 2$
(d) $1: 4$
Show Answer
Answer:
Correct Answer: 4. (c)
Solution:
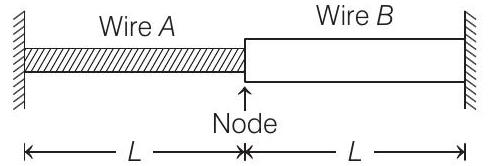
Let mass per unit length of wires are $\mu _A$ and $\mu _B$, respectively.
$\because$ For same material, density is also same.
So, $\mu _A=\frac{\rho \pi r^{2} L}{L}=\mu$ and $\mu _B=\frac{\rho 4 \pi r^{2} L}{L}=4 \mu$
Tension $(T)$ in both connected wires are same.
So, speed of wave in wires are
$$ \begin{aligned} v _A & =\sqrt{\frac{T}{\mu _A}}=\sqrt{\frac{T}{\mu}}\left[\because \mu _A=\mu \text { and } \mu _B=4 \mu\right] \\ v _B & =\sqrt{\frac{T}{\mu _B}}=\sqrt{\frac{T}{4 \mu}} \end{aligned} $$
So, $n$th harmonic in such wires system is
$$ \begin{gathered} f _{n th}=\frac{p v}{2 L} \\ \Rightarrow f _A=\frac{p v _A}{2 L}=\frac{p}{2 L} \sqrt{\frac{T}{\mu}} \end{gathered} $$
(for $p$ antinodes)
Similarly, $f _B=\frac{q v _B}{2 L}=\frac{q}{2 L} \sqrt{\frac{T}{4 \mu}}=\frac{1}{2}\left(\frac{q}{2 L} \sqrt{\frac{T}{\mu}}\right)$
$$ \text { (for } q \text { antinodes) } $$
As frequencies $f _A$ and $f _B$ are given equal.
So, $f _A=f _B \Rightarrow \frac{p}{2 L} \sqrt{\frac{T}{\mu}}=\frac{q}{2}\left[\frac{1}{2 L} \sqrt{\frac{T}{\mu}}\right]$
$$ \frac{p}{q}=\frac{1}{2} \Rightarrow p: q=1: 2 $$
