Wave Motion 2 Question 32
32. The
(1998, 2M)
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 32.
Solution:
- Since, the edges are clamped, displacement of the edges
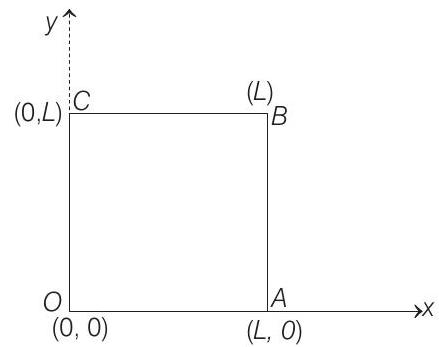
Line,
The above conditions are satisfied only in alternatives (b) and (c).
Note that






