Wave Motion 2 Question 22
22. An object of specific gravity
(a)
(b)
(c)
(d)
(1995, 2M)
Show Answer
Answer:
Correct Answer: 22. (a)
Solution:
- The diagramatic representation of the given problem is shown in figure. The expression of fundamental frequency is
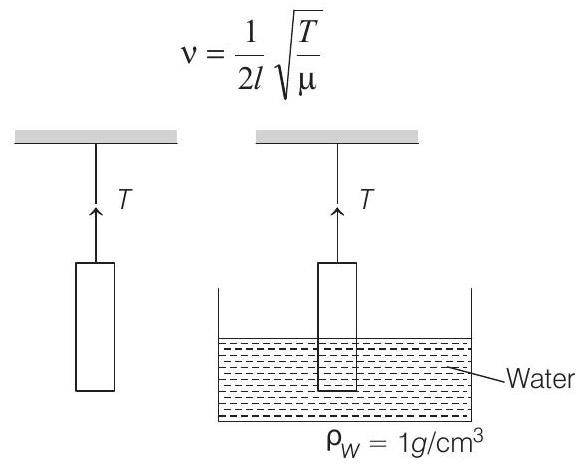
When the object is half immersed in water
The new fundamental frequency is






