Wave Motion 2 Question 11
11. A pipe of length $85 cm$ is closed from one end. Find the number of possible natural oscillations of air column in the pipe whose frequencies lie below $1250 Hz$. The velocity of sound in air is $340 m / s$.
(2014 Main)
(a) 12
(b) 8
(c) 6
(d) 4
Show Answer
Answer:
Correct Answer: 11. (c)
Solution:
- For closed organ pipe $=\frac{(2 n+1) v}{4 l}[n=0,1,2 \ldots \ldots$.
$$ \begin{array}{r} \frac{(2 n+1) v}{4 l}<1250 \\ (2 n+1)<1250 \times \frac{4 \times 0.85}{340} \\ (2 n+1)<12.52 n<11.50 \\ n<5.25 \end{array} $$
So,
So, we have 6 possibilities.
Alternate method
In closed organ pipe, fundamental node
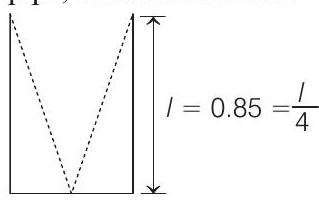
i.e. $\quad \frac{\lambda}{4}=0.85 \Rightarrow \lambda=4 \times 0.85$
As we know, $v=\frac{c}{\lambda} \quad \Rightarrow \frac{340}{4 \times 0.85}=100 Hz$
$\therefore$ Possible frequencies $=100 Hz, 300 Hz, 500 Hz, 700 Hz$, $900 Hz, 1100 Hz$ below $1250 Hz$.






