Wave Motion 1 Question 9
9. A block
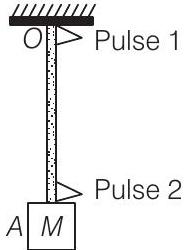 point
point
(a) The time
(2017 Adv.)
(b) The wavelength of Pulse 1 becomes longer when it reaches point
(c) The velocity of any pulse along the rope is independent of its frequency and wavelength
(d) The velocities of the two pulses (Pulse 1 and Pulse 2) are the same at the mid-point of rope
Show Answer
Answer:
Correct Answer: 9.
Solution:
since when pulse 1 reaches at
NOTE
If we refer velocity by magnitude only, then option






