Wave Motion 1 Question 11
11. A transverse sinusoidal wave of amplitude $a$, wavelength $\lambda$ and frequency $f$ is travelling on a stretched string. The maximum speed of any point on the string is $v / 10$, where $v$ is the speed of propagation of the wave. If $a=10^{-3} m$ and $v=10 m / s$, then $\lambda$ and $f$ are given by
$(1998,2 M)$
(a) $\lambda=2 \pi \times 10^{-2} m$
(b) $\lambda=10^{-3} m$
(c) $f=\frac{10^{3}}{2 \pi} Hz$
(d) $f=10^{4} Hz$
Show Answer
Answer:
Correct Answer: 11. (a, c)
Solution:
- Maximum speed of any point on the string $=a \omega=a(2 \pi f)$
$$ \begin{aligned} & \therefore \quad=\frac{v}{10}=\frac{10}{10}=1 \quad \text { (Given, } v=10 m / s \text { ) } \\ & \therefore \quad 2 \pi a f=1 \\ & \Rightarrow \quad f=\frac{1}{2 \pi a} \\ & a=10^{-3} m \\ & \therefore \quad f=\frac{1}{2 \pi \times 10^{-3}}=\frac{10^{3}}{2 \pi} Hz \end{aligned} $$
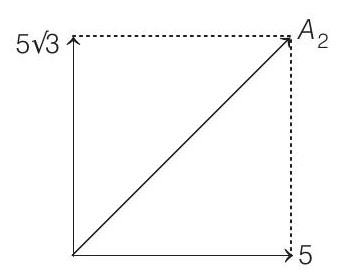
Speed of wave $v=f \lambda$
$\therefore \quad(10 m / s)=\left(\frac{10^{3}}{2 \pi} s^{-1}\right) \lambda$
$\Rightarrow \quad \lambda \quad \lambda=2 \pi \times 10^{-2} m$
