Simple Harmonic Motion 5 Question 8
13. A particle of mass $m$ is executing oscillation about the origin on the $X$-axis. Its potential energy is $U(x)=k|x|^{3}$, where $k$ is a positive constant. If the amplitude of oscillation is $a$, then its time period $T$ is
$(1998,2 M)$
(a) proportional to $1 / \sqrt{a}$
(b) independent of $a$
(c) proportional to $\sqrt{a}$
(d) proportional to $a^{3 / 2}$
Passage Based Questions
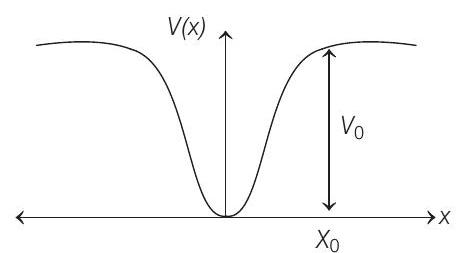
Passage
When a particle of mass $m$ moves on the $X$-axis in a potential of the form $V(x)=k x^{2}$, it performs simple harmonic motion. The corresponding time period is proportional to $\sqrt{m / k}$, as can be seen easily using dimensional analysis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of $x=0$ in a way different from $k x^{2}$ and its total energy is such that the particle does not escape to infinity. Consider a particle of mass $m$ moving on the $X$-axis. Its potential energy is $V(x)=\alpha x^{4}(\alpha>0)$ for
$|x|$ near the origin and becomes a constant equal to $V _0$ for $|x| \geq X _0$ (see figure).
(2010)
Show Answer
Answer:
Correct Answer: 13. (a)
Solution:
- $U(x)=k|x|^{3}$
$\therefore \quad[k]=\frac{[U]}{\left[x^{3}\right]}=\frac{\left[ML^{2} T^{-2}\right]}{\left[L^{3}\right]}=\left[ML^{-1} T^{-2}\right]$
Now, time period may depend on
$$ \begin{aligned} T & \propto(\text { mass })^{x}(\text { amplitude })^{y}(k)^{z} \\ {\left[M^{0} L^{0} T\right] } & =[M]^{x}[L]^{y}\left[ML^{-1} T^{-2}\right]^{z} \\ & =\left[M^{x+z} L^{y-z} T^{-2 z}\right] \end{aligned} $$
Equating the powers, we get
$$ \begin{aligned} & -2 z=1 \quad \text { or } \quad z=-1 / 2 \\ & y-z=0 \text { or } y=z=-1 / 2 \end{aligned} $$
Hence, $\left.T \propto(\text { amplitude })^{-1 / 2}\right) \propto(a)^{-1 / 2}$
$$ \text { or } \quad T \propto \frac{1}{\sqrt{a}} $$
