Simple Harmonic Motion 5 Question 5
10. A point mass is subjected to two simultaneous sinusoidal displacements in
(2011)
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 10. (b)
Solution:
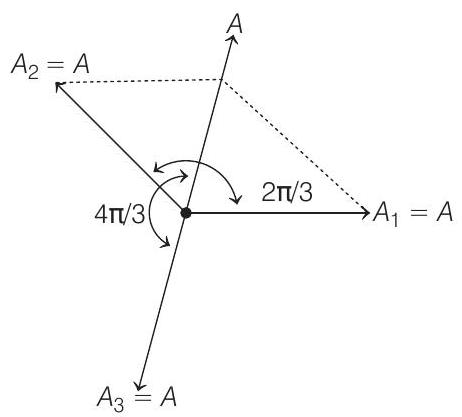
Resultant amplitude of
Alternate Solution.
It we substitute,
or
Then by applying simple mathematics we can prove that






