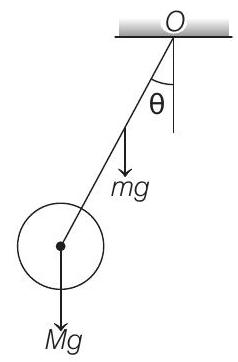
Simple Harmonic Motion 5 Question 17
22. A metal rod of length
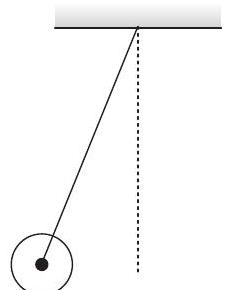performs SHM in vertical plane after being released from the same displaced position. Which of the following statement(s) is/are true?
(2011)
(a) Restoring torque in case
(b) Restoring torque in case
(c) Angular frequency for case
(d) Angular frequency for case
Show Answer
Answer:
Correct Answer: 22.
Solution:
In case
