Simple Harmonic Motion 4 Question 9
9. A block
(2004, 2M)
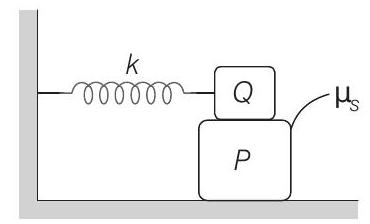
(a)
(b)
(c)
(d) Zero
Show Answer
Answer:
Correct Answer: 9. (a)
Solution:
- Angular frequency of the system,
Maximum acceleration of the system will be,
This acceleration to the lower block is provided by friction.
Hence,






