Simple Harmonic Motion 4 Question 2
2. A massless spring $(k=800 N / m)$, attached with a mass $(500 g)$ is completely immersed in $1 kg$ of water. The spring is stretched by $2 cm$ and released, so that it starts vibrating. What would be the order of magnitude of the change in the temperature of water when the vibrations stop completely? (Assume that the water container and spring receive negligible heat and specific heat of mass $=400 J / kg K$, specific heat of water $=4184 J / kg K$ )
(2019 Main, 9 April II)
(a) $10^{-4} K$
(b) $10^{-3} K$
(c) $10^{-1} K$
(d) $10^{-5} K$
Show Answer
Answer:
Correct Answer: 2. (d)
Solution:
- The given situation is shown in the figure given below
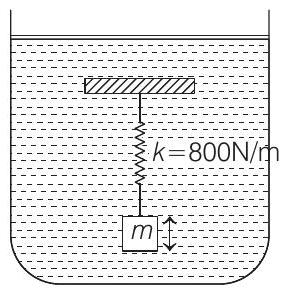
When vibrations of mass are suddenly stopped, oscillation energy (or stored energy of spring) is dissipated as heat, causing rise of temperature.
So, conversation of energy gives
$$ \frac{1}{2} k x _m^{2}=\left(m _1 s _1+m _2 s _2\right) \Delta T $$
where, $x _m=$ amplitude of oscillation,
$s _1=$ specific heat of mass,
$s _2=$ specific heat of water
and $\Delta T=$ rise in temperature.
Substituting values given in question, we have
$$ \begin{gathered} \frac{1}{2} \times 800 \times\left(2 \times 10^{-2}\right)^{2} \\ =\frac{500}{1000} \times 400+1 \times 4184 \Delta T \\ \Rightarrow \Delta T=\frac{16 \times 10^{-2}}{4384}=3.65 \times 10^{-5} K \end{gathered} $$
