Simple Harmonic Motion 4 Question 16
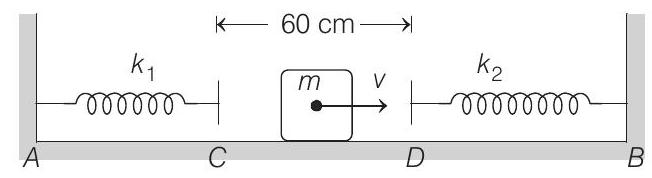
16. Two light springs of force constants
The distance
Show Answer
Answer:
Correct Answer: 16.
Solution:
- Between
Here,
and






