Simple Harmonic Motion 4 Question 15
15. Two identical balls $A$ and $B$, each of mass $0.1 kg$, are attached to two identical massless springs. The spring-mass system is constrained to move inside a rigid smooth pipe bent in the form of a circle as shown in figure. The pipe is fixed in a horizontal plane. The centres of the balls can move in a circle of radius $0.06 m$. Each spring has a natural length of $0.06 \pi m$ and spring constant $0.1 N / m$. Initially, both the balls are displaced by an angle $\theta=\pi / 6 rad$ with respect to the diameter $P Q$ of the circle (as shown in figure) and released from rest. $(1993,6 M)$
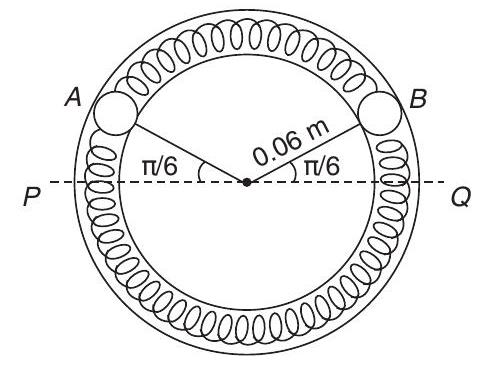
(a) Calculate the frequency of oscillation of ball $B$.
(b) Find the speed of ball $A$ when $A$ and $B$ are at the two ends of the diameter $P Q$
(c) What is the total energy of the system?
Show Answer
Answer:
Correct Answer: 15. (a) $\frac{1}{\pi} Hz$
(b) $0.0628 m / s$
(c) $3.9 \times 10^{-4} J$
Solution:
- Given, mass of each block $A$ and $B, m=0.1 kg$
Radius of circle, $R=0.06 m$
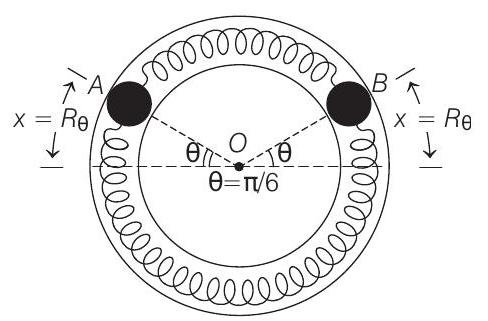
Natural length of spring $l _0=0.06 \pi=\pi R$ (Half circle) and spring constant, $k=0.1 N / m$
In the stretched position elongation in each spring
$$ x=R \theta $$
Let us draw FBD of $A$.
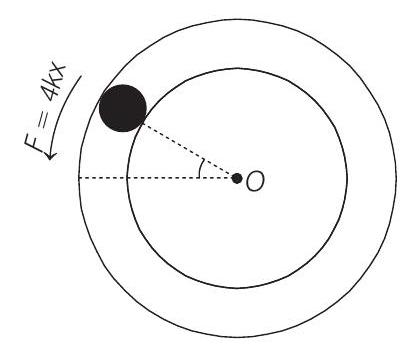
Spring in lower side is stretched by $2 x$ and on upper side compressed by $2 x$. Therefore, each spring will exert a force $2 k x$ on each block. Hence, a restoring force, $F=4 k x$ will act on $A$ in the direction shown in figure below .
Restoring torque of this force about origin
$$ \begin{array}{ll} & \tau=-F \cdot R=-(4 k x) R=-(4 k R \theta) R \\ \text { or } \quad & \tau=-4 k R^{2} \cdot \theta \end{array} $$
Since, $\tau \propto-\theta$, each ball executes angular SHM about origin $O$.
Eq. (i) can be rewritten as
$$ \begin{aligned} I \alpha & =-4 k R^{2} \theta \\ \text { or } \quad\left(m R^{2}\right) \alpha & =-4 k R^{2} \theta \\ \text { or } \quad \quad \quad & =-\frac{4 k}{m} \theta \end{aligned} $$
(a) Frequency of oscillation,
$$ \begin{aligned} f & =\frac{1}{2 \pi} \sqrt{\frac{\text { acceleration }}{\text { displacement }}} \\ & =\frac{1}{2 \pi} \sqrt{\frac{\alpha}{\theta}} \\ f & =\frac{1}{2 \pi} \sqrt{\frac{4 k}{m}} \end{aligned} $$
Substituting the values, we have
$$ f=\frac{1}{2 \pi} \sqrt{\frac{4 \times 0.1}{0.1}}=\frac{1}{\pi} Hz $$
(b) In stretched position, potential energy of the system is
$$ PE=2 \frac{1}{2} k \quad{2 x}^{2}=4 k x^{2} $$
and in mean position, both the blocks have kinetic energy only. Hence, $KE=2 \frac{1}{2} m v^{2}=m v^{2}$
From energy conservation $PE=KE$
$$ \begin{array}{rlrl} & \therefore & 4 k x^{2} & =m v^{2} \\ & \therefore \quad v & =2 x \sqrt{\frac{k}{m}}=2 R \theta \sqrt{\frac{k}{m}} \end{array} $$
Substituting the values $v=2(0.06)(\pi / 6) \sqrt{\frac{0.1}{0.1}}$
$$ \text { or } \quad v=0.0628 m / s $$
(c) Total energy of the system, $E$
$$ =PE \text { in stretched position } $$
or $=KE$ in mean position
$E=m v^{2}=(0.1)(0.0628)^{2} J$
or $E=3.9 \times 10^{-4} J$
