Simple Harmonic Motion 4 Question 14
14. A mass $m$ is undergoing SHM in the vertical direction about the mean position $y _0$ with amplitude $A$ and angular frequency $\omega$. At a distance $y$ from the mean position, the mass detaches from the spring. Assume that the spring contracts and does not obstruct the motion of $m$. Find the distance $y$ (measured from
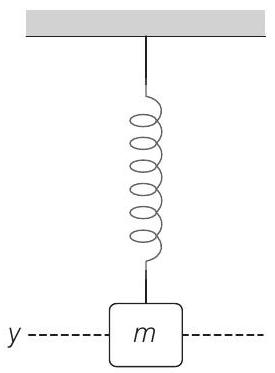the mean position) such that the height $h$ attained by the block is maximum. $\left(A \omega^{2}>g\right)$.
(2005)
Show Answer
Answer:
Correct Answer: 14. $\frac{g}{\omega^{2}}$
Solution:
- At distance $y$ above the mean position velocity of the block.
$$ v=\omega \sqrt{A^{2}-y^{2}} $$
After detaching from the spring net downward acceleration of the block will be $g$.
Therefore, total height attained by the block above the mean position,
$$ h=y+\frac{v^{2}}{2 g}=y+\frac{\omega^{2}\left(A^{2}-y^{2}\right)}{2 g} $$
For $h$ to be maximum $d h / d y=0$
Putting $\frac{d h}{d y}=0$, we get $y=\frac{g}{\omega^{2}}=y _{\max }$
