Simple Harmonic Motion 4 Question 12
12. A particle of mass
(2013 Adv.)
(a) the speed of the particle when it returns to its equilibrium position is
(b) the time at which the particle passes through the equilibrium position for the first time is
(c) the time at which the maximum compression of the spring occurs is
(d) the time at which the particle passes through the equilibrium position for the second time is
Numerical Value
Show Answer
Answer:
Correct Answer: 12. (a, d)
Solution:
- At equilibrium
writing,
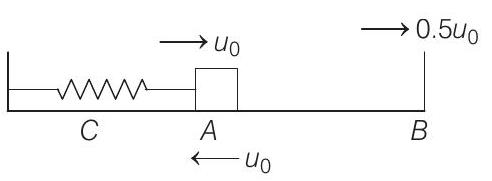
(b)
(c)
(d)






